活用变式理论 强化数学思想*——关于一类圆锥曲线中心弦与准线问题的探讨

惠州市惠阳中山中学(516211) 朱天辉

惠州学院数学与统计学院(516007) 王海青

1 基于变式理论的习题课教学结构

变式教学理论是中国数学教育的特色与智慧结晶,最早由顾泠沅教授带领团队基于“青浦实验”数学教学改革成果的凝练[1-6].变式是指教师在教学中有目的有计划地变换材料的形式,对命题进行适当的条件或结论转化,在变换过程中探究不变的规律和性质,从而掌握数学对象的本质属性.变式教学分为概念性变式和过程性变式两类,其中过程性变式主要聚焦于问题解决,有层次地推进问题解决的过程中构建联系紧密富有逻辑的数学知识体系.

习题课的有效开展有助于促进学生的深度学习,它是对概念和原理的进一步巩固和深化,是在问题解决的过程中引导学生探究,使之掌握相应的知识与思想方法并学会思考.基于已有的变式教学理论,研究对过程性变式的结构和策略进一步细化,构建形成数学习题课教学的基本结构,如图1.该结构表明,习题课的教学过程可以大致分为两部分.首先是提出一个有代表性或典型性的问题,为了解决这个问题可能需要通过类比与特殊化的思想将问题变得更为简单和容易求解,在解决特殊问题的过程中获得一些特殊的结论与方法,从而为解决原问题找到方向或思路.原问题得到全面解决后,再运用类比和一般化的思想将之进行拓展推广,得到变式1、变式2 等问题,为了解决这些新的问题通常又需要经过一般到特殊、化未知为已知、化繁为简的化归变式不断向已知的、熟悉的问题靠拢,最后得到一般性的结论与方法.

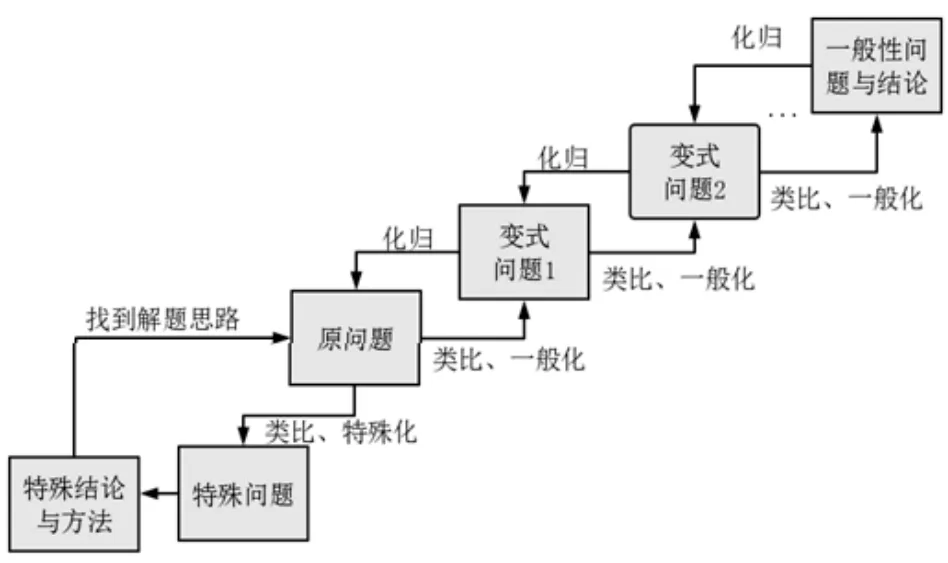
图1

2 对一类圆锥曲线中心弦与准线问题的探讨

下面结合数学习题课教学的基本结构,以一道关于椭圆中心弦与准线的最值问题为例展开习题课的探究教学,最后得到一类圆锥曲线中心弦与准线问题的解决方法以及一般性结论,在整个教学探究过程中一直注重数学思想方法的渗透与强化.

问题1如图2,椭圆=1 中,A,B分别椭圆的左右顶点,l是椭圆的右准线,点P是椭圆上异于A,B的动点,直线AP、BP分别交l于M,N两点,求线段MN的最小值.

图2

(1)常规思路,顺势求解

分析本题考查圆锥曲线的动点与最值问题,根据题目的条件学生常会想到以下两个思路.思路1:直接设P点坐标,再利用直线AP、BP的方程与直线l相交求出M,N两点坐标,然后根据两点间的距离公式及年巴尔干数学奥林匹克试题,文献基本不等式求出线段MN的最小值;思路2:设M,N两点坐标,利用直线MA、NB的交点为P且P在椭圆上的条件进行求解.这两个思路比较简单直接但计算较为繁琐,具体解答如下.

(2)反思过程,优化解法

直接从题目的条件看,似乎没有什么特别隐含的信息.如果将问题条件特殊化,把“椭圆”变为“圆”,其它条件不变,此时AB则变为圆的直径,点为圆上一动点.

显然,由直径所对的圆周角是直角这一结论容易得到,直线AP,BP的斜率之积为一定值-1.于是猜想:如果是椭圆,直线AP,BP的斜率之积也为某一定值.不难证明这个结论,具体过程如下.

运用这个结论,上述两个解法将大大简化解答过程和减少运算量.

优化解法1解题思路与解答过程如下,

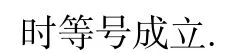
优化解法2解题思路与解答过程如下,

(3)归纳升华,提炼性质

如图2,点P为椭圆上异于长轴两端点A,B的动点,则直线AP,BP的斜率之积为一定值.如果线段AB为过椭圆中心的任一条弦,称之为椭圆的中心弦,如图3.此时,直线AP,BP的斜率之积是否为一定值? 不难证明,其斜率之积仍为定值.

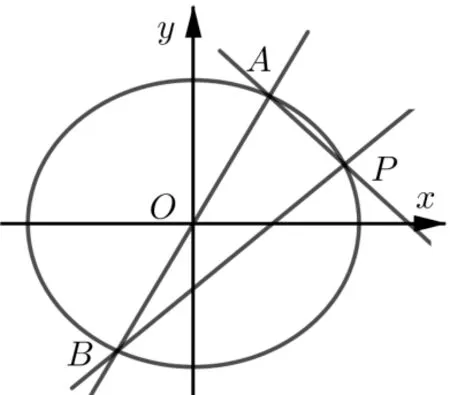
图3

性质1椭圆=1 中,过椭圆中心的直线交椭圆于A,B两点,P为椭圆上异于A,B的一动点,则当直线AP,BP斜率存在时,斜率之积为-1+e2.

在历年的高考数学中,也有不少考题将椭圆的中心弦融入其中,比如下面这道题.

高考链接(2011 年高考江苏卷第18 题)如图4,在平面直角坐标系xOy中,M,N分别是椭圆=1 的顶点,过坐标原点的直线交椭圆于P,A两点,其中P在第一象限.过P作x轴的垂线,垂足为C.连接AC,并延长交椭圆于点B.设直线PA的斜率为k.对任意k ＞0,求证:PA⊥PB.

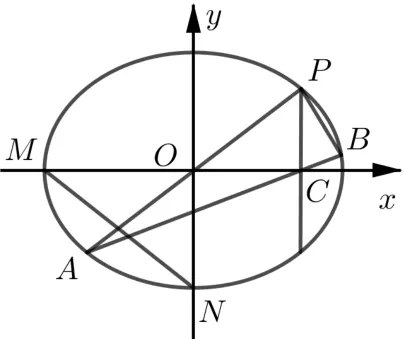
图4

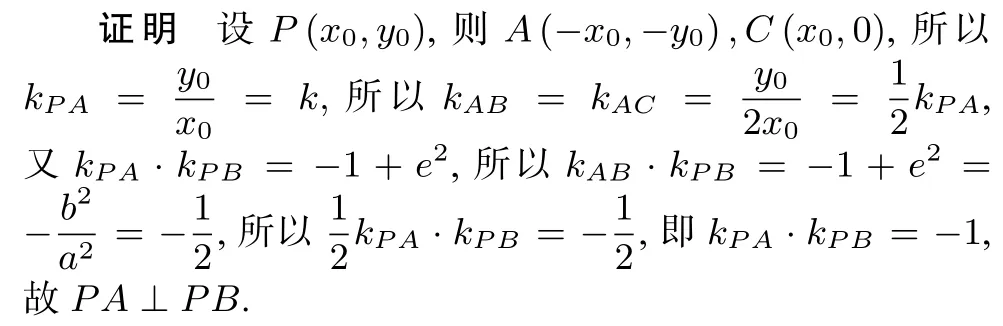
根据前面的探究和性质1,可以对问题1 的条件进行弱化,得到如下更一般的问题2.

问题2如图5,椭圆=1 中,过椭圆中心的直线l1交椭圆于A,B两点,l是椭圆的右准线,点P是椭圆上异于A,B的动点,直线AP、BP分别交l于M,N两点,求线段MN的最小值.

图5

(4)拓展延伸,变式提升

自然地会提出这样一个问题,关于椭圆中心弦的性质及其与准线相关的最值问题,是否也可以类比到双曲线上? 通过类似的方法探究,同样可以得到类似的结论和问题.

性质3双曲线=1 中,过双曲线中心的直线交双曲线于A,B两点,P为双曲线上异于A,B的一动点,则当直线AP,BP斜率存在时,斜率之积为-1+e2.

3 小结

习题课的教学应重视围绕一个问题展开多角度多层次的探讨,在一题多解中深入理解问题的本质.进而通过变式拓展将问题一般化,在这个过程中突出通性通法的讲解,得出一般性的方法与结论,最终引领学生形成整体的数学知识体系.特别地,习题课的教学应重视解题思路的剖析,将数学思想方法贯穿始终,关注数学思维的培养,通过教学教会学生思考发展核心素养.当然,在拓展延伸的过程中应注意结合学生的实际把握适当的广度、深度和难度,比如前面的问题2,一般性的问题对于大部分学生还是有一定困难.但教师应该能站在更高的角度看待这类问题,具备更完善丰富的知识,以便能根据学生情况高屋建瓴地对问题的条件和结论进行灵活处理.