配电网运行状态空间的安全性分布：特征及应用

肖 峻，焦 衡，宋晨辉，屈玉清

配电网运行状态空间的安全性分布：特征及应用

肖 峻1，焦 衡1，宋晨辉2，屈玉清1

(1. 智能电网教育部重点实验室(天津大学)，天津 300072；2. 国网能源研究院有限公司，北京 102209)

随着智能电网建设，我国城市配电网的调度运行将变得更精细，深入研究配电网运行的状态空间十分必要，特别是调度部门关心的安全性问题．本文研究了配电网运行状态空间的安全性分布．首先，为建立系统状态(工作点)和安全性结果间的映射关系，设计了两种计及主变容量约束的安全函数，用来量化系统的安全程度．其次，提出了运行状态空间安全性分布的概念，状态空间内所有工作点及其安全函数值构成了安全性分布．然后，在IEEE RBTS-Bus4扩展算例中验证了所提概念和方法，并绘制了算例配电网的状态空间安全性分布图．研究发现，在状态空间中，安全性分布形成了一种类似自然界电场、磁场的“安全性场”，其分布特征如下：以空载点为中心呈“等安全线”形式分布，并且具有单调减的自然特性，即距离中心越远，等安全线值越低．等安全线的法线方向是安全性变化最快方向，也是安全性提高的最优控制方向．

配电网；运行状态空间；安全性分布；安全函数

安全性是电力系统规划运行需要考虑的重要问题．在安全性分析中，“域”方法相较于传统逐点法具有诸多优越性[1]，如能提供工作点(系统状态)在域中的位置、提高安全分析速度等．“域”方法起源于输电系统，自提出以来一直受到关注，目前输电网安全域已在模型[2-3]、算法[4]及拓扑性质[4-6]等方面取得了重要进展，并不断深入应用[6-7]．

近年来，配电网安全域(distribution system security region，DSSR)成为研究热点，它定义为配电系统所有满足一定安全准则工作点的封闭集合[8]．DSSR的存在性已通过仿真观测[9]、数学推导[10]和实证研 究[11]3条途径得到验证，其后续研究涉及模型[8,12-14]、算法[15]、性质机理[15-16]及方法应用[17-21]等，基本形成理论体系．DSSR的概念与方法也还扩展到舰船综合电力系统[22-23]、综合能源系统[24-26]及能源互联网[27]等领域．

安全域在配电安全评估中扮演着重要角色．文献[8]提出了基于DSSR的配电安全评价方法．文献[11]基于DSSR对天津市城南区夏季大负荷数据进行了安全分析．文献[19]基于安全域提出了考虑-1安全的分布式电源(distributed generation，DG)出力控制可视化方法．文献[28]基于安全域对工作点当前及未来状态的安全性进行“态评估”．文献[29]将安全域应用于有功安全校正的评估及控制．安全边界是基于安全域进行安全评估的关键部分．文献[16]总结发现了配电安全边界的形成机理和规律，文献[30]将配电安全边界细分为严格边界与非严格边界，能提高实时安全评估的效率．现有安全性研究的重点是安全边界，对整个运行状态空间，也只是宏观指出安全边界内工作点是安全的，边界外工作点是不安全的．

随着智能电网的建设，大中城市配电网正逐步实现自动化、信息化和智能化，调度运行变得精细，深入研究配电网状态空间十分必要．目前，完整状态空间的安全程度鲜见研究报道，其中安全性分布的特征还是未知领域．这带来了一些令人感兴趣的问题：配电状态空间中的安全性分布是否规律性存在，分布特征是什么，有何应用价值．本文开展了针对性研究工作，试图回答这些问题．

1 配电系统运行状态空间与安全域

1.1 配电系统运行状态空间

配电系统运行状态空间定义为所有可行范围内工作点构成的集合，记为．其中，工作点指能唯一描述配电网安全性的最少状态变量的集合，记为．对于有回馈线或馈线段的配电系统，有

式中：为馈线出口负荷的视在功率；S,min为S下限，缺省值为0；S,max为S上限，由馈线上所接配变总容量确定．

式(1)采用馈线出口负荷表示工作点，这是因为配电系统节点数多，分析中可以归并，而且很多节点没有实时量测，而馈线出口有准确的量测．

式(2)为状态空间表达式，是工作点的定义域，且是有界的[10,30]．

1.2 配电系统的N-1安全性

为保障安全可靠供电，我国城市配电系统普遍采用-1安全准则，配电网安全性和安全域的研究也大都基于-1准则，故本文聚焦于-1安全性．

配电系统的-1安全性指：某工作点下，发生单一元件退出运行，通过必要的故障隔离和恢复操作后，非故障区域负荷仍能持续供电，且系统仍满足元件容量与电压等运行约束．若满足，称该工作点关于此元件-1安全，否则不安全．-1准则要求配电网所有元件单一故障后，系统均能满足-1安全性．

1.3 配电系统安全域与安全边界

1.3.1 配电系统安全域

DSSR定义为状态空间中满足条件C1～C4的安全工作点的集合，记为DSSR[10]．C1：集合存在边界点；C2：边界封闭；C3：边界围成的内部空间中，所有工作点都安全；C4：边界外所有工作点都不安全．

对于有回馈线或馈线段的配电系统，基于馈线互联关系的DSSR模型[14]可表述为

本文模型简化处理了网损与电压约束，原因是城市地区馈线较短，一般采用电缆，网损较小；且可通过无功补偿设备和变压器分接头调压，电压降落不大，电压约束不难满足．基于交流潮流的配电网安全域研究也表明[31]，简化考虑网损和电压约束的安全域误差不大，可满足城网需求．

式(3)可化为个最简式，即

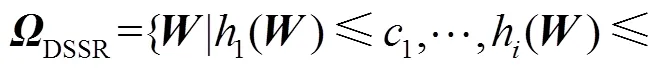
式中h()和c分别是式(3)各式左端和右端的简化表达形式，＝1，2，…，．

1.3.2 安全边界

DSSR具有明确边界，可由线性、紧致且不会“打结”的超平面描述[15]．由式(4)得到DSSR第个有效安全边界[32]的表达式为

其简洁形式为

式中∈DSSR相当于不等式约束，确保等式约束在DSSR范围内．

将各β求并集，得到完整的安全边界∂DSSR为

由此可见，DSSR由个超平面边界围成．当配电系统的拓扑结构与元件容量确定时，DSSR在状态空间中唯一确定[6,9]．负荷和DG波动、运行方式及网络重构等仅影响工作点位置，不影响DSSR．

1.4 安全距离

在安全域分析方法中，安全距离是系统安全评价的基础工具，它在输电系统中被首先提出[33]和应 用[34-35]．文献[1]将安全距离引入配电网，用一种馈线负荷裕度表示安全距离．文献[32]规范了配电安全距离的概念，定义为工作点到安全边界的距离．安全距离为正，工作点位于域内，系统安全，反之不安全．安全距离的大小体现了负荷裕度．

本文基于文献[36]的域轴向几何距离和域最短状态距离来描述安全性分布，以下介绍这两种距离的定义与计算方法．

域轴向几何距离为工作点沿某个坐标轴方向出发碰到第1个安全边界的几何距离，即

域最短状态距离为工作点到所有安全边界的最短状态距离，其数学表达式为

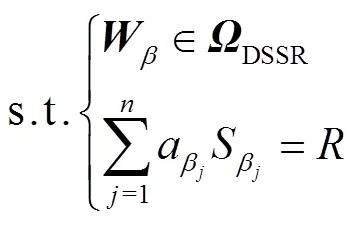
综上，R-AGD能反映域内点在某个轴向的负荷裕度，可用于描述域内点的安全程度；R-SSD能反映域外点回到安全状态的最小控制代价，可用于描述域外点的不安全程度．

2 安全函数

安全函数利用解析的函数关系，建立了状态空间中工作点与安全性结果间的映射关系，为描述状态空间安全性分布奠定了基础．文献[10]在证明DSSR存在性时，首次提出了配电网安全函数的概念．文献[10]安全函数未考虑主变容量约束，可能会造成某些工作点安全性判断不准确[14]．为此，本文设计了能计及主变容量约束的安全函数．

2.1 安全函数的通用定义与性质

在配电系统安全性分析中度量系统状态安全或不安全程度的函数，称为安全函数．-1安全下的安全函数记为f-1．

安全函数的自变量是中的任意工作点，函数值是该点的安全性结果．

安全函数需要满足以下性质[10]．

1) 连续性

状态空间反映了安全函数的定义域．f-1在状态空间中任意点连续，可知f-1在整个状态空间中 连续．

2) 正负号和大小

工作点安全时安全函数值为正，不安全时为负，临界安全时为0．

安全函数值能评价某个工作点的安全程度：函数值越大，系统越安全；反之越不安全．

3) 单调减性

对于任意工作点，增加其任意1个或多个维度的负荷功率，将得到一个新工作点，在这个过程中安全性一般会降低，至少不会提高；新工作点的安全函数值需小于等于原工作点的安全函数值．本文将这一性质称为广义单调减性．

对于任意工作点，增加其任意1个或多个维度的负荷功率，将得到一个新工作点，在这个过程中安全性降低；新工作点的安全函数值需小于原工作点的安全函数值．本文将这一性质称为严格单调减性．

安全函数满足严格单调减性时，也一定满足广义单调减性，反之不成立．

4) 空载点最大

空载点是最安全的，因此安全函数的最大值在空载点取到，即max{f-1()}＝f-1(0)．

2.2 本文的两种安全函数

本文设计了两种安全函数，它们反映安全性的细致程度不同：Ⅰ型安全函数反映工作点的基本安全性；Ⅱ型安全函数对Ⅰ型安全函数等值点的安全性进一步区分．实际使用中可根据安全性分析的需要 进行选择．以下介绍这两类函数的设计思路与计算方法．

2.2.1 Ⅰ型安全函数

本文设计Ⅰ型安全函数的思路如下：在状态空间中，域内点的安全程度与其在各轴向上到-1安全边界的负荷裕度相关；域外点的不安全程度则与其回到-1安全边界的控制代价相关．安全距离描述了上述信息．针对域内点，采用域轴向几何距离R-AGD作为判据；针对域外点，采用域最短状态距离R-SSD作为判据．

定义Ⅰ型安全函数f-1，Ⅰ如下．

式中R-AGD,j为工作点在S轴向上的域轴向几何 距离．

Ⅰ型安全函数满足安全函数的4个性质，该函数通过工作点到各安全边界的安全距离最小值来评价系统安全程度．安全边界通过式(3)～式(7)计算得到，式(3)同时计及了馈线容量约束和主变容量约束.

式(12)表明，域内点的f-1,Ⅰ值反映了其在整个域最危险方向上的负荷裕度；域外点的f-1，Ⅰ值反映了其回到安全状态的最小控制代价．

具体安全函数的选取并不唯一．Ⅰ型安全函数基于安全距离最小值，对于安全距离最小值相等的工作点，认为其安全性相同．而这些工作点到不同边界的距离一般是不同的，当工作点在域内时，这意味着到不同边界的负荷裕度不同，因此它们的安全性有更细微的差别．例如，f-1，Ⅰ相等的严格边界点在各轴向的裕度均为0，而非严格边界点至少在一个轴向存在裕度[30]，故后者安全程度更高．

2.2.2 Ⅱ型安全函数

为反映上述差别，本文设计了Ⅱ型安全函数．

定义Ⅱ型安全函数f-1,Ⅱ如下．

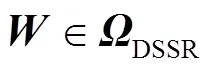
式(13)表明，域内工作点的f-1,Ⅱ值反映了其在整个域各轴向上的负荷裕度之和．

需要指出，Ⅱ型安全函数仅用于区分域内点的安全程度，域外仍沿用Ⅰ型安全函数，原因如下：当工作点位于域外时，最关注如何调整工作点，即应按照Ⅰ型安全函数值增大最快的方向调整工作点，使其尽快回到域内，进一步区分域外Ⅰ型安全函数等值点不安全程度的迫切性不高．

3 运行状态空间的安全性分布及观测

3.1 状态空间安全性分布

配电网运行状态空间内所有工作点及其安全性分析结果构成了状态空间安全性分布，记为．

状态空间工作点无穷多，通过等步长抽样[37]生成有限个能代表状态空间的工作点样本，记为， 则有

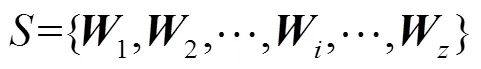
式中为抽样点数量．

对中所有点进行安全性分析可得到状态空间安全性抽样分布，记为SD．安全性抽样分布用来近似安全性分布，以下统称安全性分布．

为观察状态空间安全性的分布特征，借鉴物理中等势线、等温线图，将安全函数值相同的点连接，得到“等安全线”，形成配电网状态空间安全性分布图．

对于采用-1安全准则的配电网，状态空间内所有工作点及某种安全函数值构成了配电网状态空间-1安全性分布，记为SD-1，则有

连接式(15)中函数值相等的工作点，得到配电网状态空间-1安全性分布图．

3.2 安全性分布与安全域的区别

安全性分布与安全域DSSR的区别如下．

(1) 范围更大：DSSR的描述范围是安全域(含边界)内，不含域外；安全性分布将描述范围扩展到域外，即整个状态空间．

(2) 安全信息更详细：DSSR只是描述域内是安全的，域外是不安全的，边界上是临界安全的；安全性分布除描述安全不安全外，还能给出任意工作点的安全或不安全程度，即该点的安全函数值．

(3) 信息量更大：安全性分布在状态空间中以“等安全线”分布，DSSR边界是其中一条特殊的“等安全线”．因此，安全性分布包含了DSSR，能直接得到DSSR；而DSSR信息没有包括状态空间安全性分布．

3.3 安全性分布的观测方法

安全性分布由状态空间中的安全函数等值线/面构成，与DSSR具有相似的高维几何特征．因此，现有的DSSR观测方法对安全性分布的观测也有借鉴意义．

DSSR观测包括二维投影观测和全维直接/间接观测．其中，二维观测是选择高维DSSR的某个工作点和2个关联的观测变量，得到该点下DSSR的二维投影断面[8-9]；全维直接观测[38]是在三维坐标系中展现低维DSSR的全貌；全维间接观测[39]是利用域半径折线图和雷达图反映高维DSSR的形态和特征．此外，供电能力曲线[37]反映了DSSR严格安全边界的效率，也可视为对DSSR的观测．

本文研究状态空间安全性分布，采用二维投影观测方法，该方法的详细步骤如下：

步骤1 依据式(3)～式(7)列写边界表达式；

步骤2 选择两个相关变量作为观测变量，非观测变量固定为常数，化简边界表达式；

步骤3 在以观测变量构成的坐标系中绘制化简后方程对应的边界线；

步骤4 边界线及坐标轴围成的封闭图形即为域的二维投影图像．

4 算例分析

4.1 算例简介

为贴近我国城市中压配电网的实际情况，在IEEE RBTS-Bus4算例[40]基础上，增加馈线和联络，如图1所示．算例包含3座35kV变电站，6台35/10kV主变，19回10kV馈线．设主变容量为16.0MV·A，馈线容量为6.0MV·A，单回馈线配变总容量为7.0MV·A．

RBTS扩展算例的安全域及状态空间表达式分别如表1和表2所示．

4.2 安全函数值计算结果

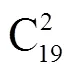
以馈线负荷1、8为观测变量，非观测变量固定在工作点＝(1，3.0，0，5.0，0，3.0，0，0，8，6.0，0，4.0，4.0，0，1.0，2.0，0，1.0，3.0，5.0)．

进一步，以1.0MV·A为步长，在(1，8)形成的二维状态空间中取得64个抽样点．利用式(12)、(13)计算抽样点的两种安全函数值，结果如表3所示.

4.3 状态空间安全性分布

4.3.1 Ⅰ型函数安全性分布

连接表3中f-1,Ⅰ等值点，得到“f-1,Ⅰ等安全线”(点线)，可视化后如图2所示．等安全线旁保留1位小数的数值为f-1,Ⅰ值．

图1 IEEE RBTS-Bus4扩展算例的网络结构

表1 安全域表达式

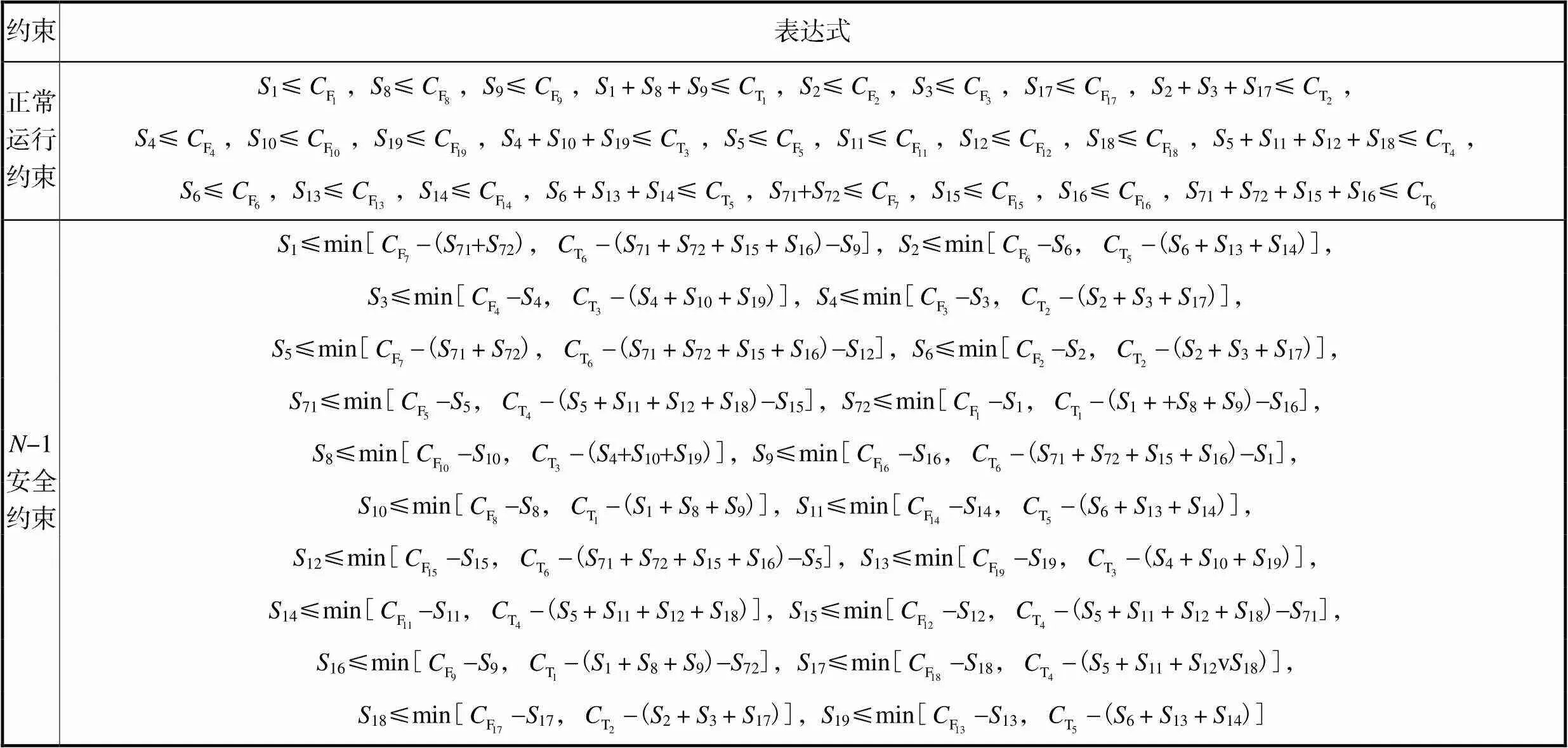
Tab.1 DSSR expressions

表2 状态空间表达式

Tab.2 State space expressions

表3 安全函数值计算结果

Tab.3 Calculation results of the security function

图2 状态空间中Ⅰ型函数安全性分布

从图2看出，安全性分布具有以下特征．

(1) 域内f-1,Ⅰ＞0，系统安全，空载点最安全，f-1,Ⅰ＝6.0；安全边界上f-1,Ⅰ＝0，系统临界安全；域外f-1,Ⅰ＜0，系统不安全，满载点最不安全，f-1,Ⅰ＝-4.0．

(2) 安全性呈“等安全线”形式分布．等安全线均匀分布，即任意两相邻等安全线之间的距离是相等的；等安全线由平行于安全边界的直线和斜线构成．等安全线长度从点开始先变长后变短，与状态空间边界部分重合时达到最长(图2中)．

(3) 工作点位于斜线等安全线上时，安全性满足严格单调减性，即任意方向增长负荷(工作点沿坐标轴正向移动)，安全性都降低；工作点位于直线等安全线上时，安全性满足广义单调减性，即工作点沿直线等安全线增长负荷时，安全性不变，而沿其垂向增长负荷时安全性降低．

4.3.2 Ⅱ型函数安全性分布

同理，连接表3中-1,Ⅱ等值点，绘制“-1,Ⅱ等安全线”(虚线)，可视化后如图3所示．

从图3看出，Ⅱ型函数安全性分布继承了Ⅰ型函数安全性分布的大量特征，但也略有区别．

(1) 安全边界上函数值不同：非严格边界、上f-1,Ⅱ＞0；严格边界上f-1,Ⅱ＝0．

(2) 等安全线形状不同：等安全线间的过渡更为平滑，等安全线不再与域边界平行，由一条或多条不同斜率的“斜线等安全线”构成，无“直线等安全线”.

(3) 图3中状态空间所有工作点均满足严格单调减性，而在图2所示的Ⅰ型函数分布图中，直线点满足广义单调减性．

图3 域内Ⅱ型函数安全性分布

Ⅱ型函数可进一步判断域内Ⅰ型函数等值点的安全程度．在图2中，工作点、的f-1,Ⅰ值均为0，此时Ⅰ型函数无法区分、的临界安全程度；在图3中，工作点、的f-1,Ⅱ值分别为0、8.0，的安全程度更高，这与工作点在1方向存在负荷裕度而点在任意方向不存在裕度的事实相符．

4.4 安全性分布特征的一般性解释

由第4.3节IEEE RBTS-Bus4算例观测结果可知，配电网状态空间安全性分布的特征是以空载点为中心呈“等安全线”形式分布，具有单调减的自然特性．这些特征具有一般性，解释如下．

特征1：具有单调减的自然特性．

解释：安全性分布由工作点及其安全函数值构成．安全函数在状态空间中满足单调减性，即对于任意工作点，增加其任意一个或多个维度的负荷功率，将得到一个新工作点，在这个过程中域内点在各方向的负荷裕度将减小或不变，所以系统安全性一般会降低，至少不会提高，故新工作点的安全函数值小于或等于原工作点的安全函数值．安全性分布是基于安全函数值描述的，继承了其单调减的性质．

特征2：以空载点为中心呈“等安全线”形式分布.

解释：①由安全函数定义域(状态空间)和单调减性可知，其函数最大值在零点取到，即空载点的安全函数值最大、最安全；②由安全函数的连续性和单调减性可知，在沿任意方向远离空载点的过程中，工作点的安全函数值均是在最大值的基础上连续且单调减小．因此，在不同方向上均会存在函数值相同的点，将这些点连接会得到一系列以空载点为中心的“等安全线”．这些等安全线不会相交，因为安全函数是通过工作点到各安全边界的安全距离最小值来评价的，最小值是唯一的．若等安全线相交，则表明相交处的工作点有两个“最小值”，这是不存在的．

4.5 与自然界中物理场的对比

配电状态空间安全性分布形成了一种“安全性场”，将其与自然界中物理场对比．以静电场为例，如图4所示．

静电场中存在电势分布．单个点电荷在与其相距为处激发的电势＝/，为静电力常量[41].设某电荷静止于原点，且＝1，由MATLAB的Contour函数绘制其静电场电势分布，得到图4(a).将图2中等安全线条数增加1倍，得到图4(b).

从图4看出，两种分布具有相似的特征：静电场的激发源是点电荷，此点的电势最高；安全场的激发源是空载点，此点的系统安全性最高．电势以“等势线”分布，以点电荷为中心，随距离增加，电势单调减小；安全性以“等安全线”分布，以空载点为中心，随距离增加，安全性单调减小．可见，安全性场具有类似自然界电场、磁场的特点．

5 应用举例

本文得到配电状态空间的安全性分布，在调度运行中能做到安全域不易做到的功能．以算例结果图5为例说明．

图5 安全性分布的应用

5.1 安全评价中的应用

等安全线更直接地描述了运行状态空间不同位置的安全程度．例如，在图5中，工作点1(5.0，1.0)、2(3.0，3.0)总负荷均为6.0MV·A，但位于不同等安全线上．从等安全线值易看出，2更安全，安全程度3.0MV·A，1为1.0MV·A．而只得到安全域时，能直接判断出1和2都在域内，是安全的．如需度量安全程度时，则需进一步计算到所有安全边界的距离[32]．

5.2 优化控制中的应用

安全性分布还指示了相同负荷水平下的最优负荷分布．例如，在图5中，轨迹1上是总负荷均为6.0MV·A的不同负荷分布的工作点，轨迹1与等安全线相交，定位到2是最安全的负荷分布，这是网络重构优化工作点的结果．而只得到安全域时，很难直接得到这一结果，除非进一步建立优化模型求解.

5.3 预防控制中的应用

等安全线的法线方向代表了安全性变化最快的方向，可沿此方向最快速调整工作点的安全性．当工作点位于域外时，法线方向是域外点回到安全域内或提高安全程度的最优控制方向，调度员可据此采取预防控制措施[9]．例如，在图5中，工作点3(6.0，6.0)位于域外，系统不安全．沿等安全线的法线方向，安全程度变化最快，负荷变化最小，即控制代价最小.沿轨迹2回到域内，是对3的最优预防控制方向.而只得到DSSR很难直接得到这一结果，除非进一步建模优化．

上述应用举例是在二维空间进行的，此时等安全线由平行于安全边界的直线和斜线构成，其法线方向很容易确定．在高维状态空间中，等安全线扩展为超平面，其法线方向的确定步骤如下．

步骤1 确定当前工作点．

步骤2 计算该工作点到所有安全边界的安全距离，距离最小值对应的边界称为目标安全边界．

需指出，当前工作点所在超平面与目标安全边界平行，这是因为目标安全边界由距离最小值(记为min)确定，min也是当前工作点及其所在超平面的安全函数值．若该超平面与目标安全边界不平行，则在该超平面上，存在一部分工作点到目标安全边界的距离大于min，而另一部分工作点到目标安全边界的距离小于min．后者会导致的安全函数值小于min，与事实不符．故当前工作点所在超平面一定平行于目标安全边界．

步骤3 依据边界表达式求取目标安全边界的法线方向，该方向也是当前工作点所在超平面的法线方向，即等安全面法线方向．

6 结 论

本文研究了配电网整个运行状态空间的安全性，主要贡献如下．

(1) 提出了配电网状态空间安全性分布的概念；设计了两个能计及主变容量约束的安全函数，来量化系统安全程度．

(2) 揭示了配电网的安全性分布特征：以空载点为中心呈“等安全线”分布，形成类似电场、磁场的“安全性场”，具有单调减的自然特性．

(3) 在IEEE RBTS-Bus4扩展算例中验证了本文方法，完整绘制了配电网状态空间安全性分布图，现有文献中的安全边界[10]是其中一条“等安全线”.

(4) 基于算例展示了安全性分布在安全分析、优化控制和预防控制上的应用．相比于安全域，安全性分布不仅能提高安全分析的速度，还能不经优化直接得到优化控制和预防控制的结果．

相比于安全边界，本文对完整认识配电网运行状态空间的安全性质具有重要价值．本文研究针对城市配电网，后续研究将扩展到农网以及含DG、储能等多种类电源的主动配电网，考虑电压约束；并从高维状态空间观测安全性全貌．

［1］ 余贻鑫. 安全域的方法学及实用性结果[J]. 天津大学学报，2003，36(5)：525-528.

Yu Yixin. Methodology of security region and practical results[J]. Journal of Tianjin University，2003，36(5)：525-528(in Chinese).

［2］ Wu F F，Kumagai S. Steady-state security regions of power systems[J]. IEEE Transactions on Circuits and Systems，1982，29(11)：703-711.

［3］ 冯 飞，余贻鑫. 电力系统功率注入空间的动态安全域[J]. 中国电机工程学报，1993，13(3)：16-24.

Feng Fei，Yu Yixin. Dynamic security regions of power system in injection spaces[J]. Proceedings of the CSEE，1993，13(3)：16-24(in Chinese).

［4］ 余贻鑫，李 鹏，孙 强，等. 电力系统潮流可行域边界拓扑性质及边界算法[J]. 电力系统自动化，2006，30(10)：6-11.

Yu Yixin，Li Peng，Sun Qiang，et al. Study on topological properties of boundary of power flow feasibility region and algorithm for boundary computation[J]. Automation of Electric Power Systems，2006，30(10)：6-11(in Chinese).

［5］ Yu Yixin，Zeng Yuan，Feng Fei. Differential topological characteristics of the DSR on injection space of electrical power system[J]. Science in China Series E：Technological Science，2002，45(6)：576-584.

［6］ Yu Yixin，Liu Yanli，Qin Chao，et al. Theory and method of power system integrated security region irrelevant to operation states：An introduction[J]. Engineering，2020，6(7)：754-777.

［7］ 王曦冉，章敏捷，邓 敏，等. 基于动态安全域的最优时间紧急控制策略算法[J]. 电力系统保护与控制，2014，42(12)：71-77.

Wang Xiran，Zhang Minjie，Deng Min，et al. Optimal emergency control strategy algorithm of ideal time based on dynamic security region[J]. Power System Protection and Control，2014，42(12)：71-77(in Chinese).

［8］ Xiao Jun，Gu Wenzhuo，Wang Chengshan，et al. Distribution system security region：Definition，model and security assessment[J]. IET Generation，Transmission & Distribution，2012，6(10)：1029-1035.

［9］ Xiao Jun，Zu Guoqiang，Gong Xiaoxu，et al. Observation of security region boundary for smart distribution grid[J]. IEEE Transactions on Smart Grid，2017，8(4)：1731-1738.

［10］ 肖 峻，祖国强，白冠男，等. 配电系统安全域的数学定义与存在性证明[J]. 中国电机工程学报，2016，36(18)：4828-4836.

Xiao Jun，Zu Guoqiang，Bai Guannan，et al. Mathematical definition and existence proof of distribution system security region[J]. Proceedings of the CSEE，2016，36(18)：4828-4836(in Chinese).

［11］ 肖 峻，祖国强，贺琪博，等. 配电网安全域的实证分析[J]. 电力系统自动化，2017，41(3)：153-160.

Xiao Jun，Zu Guoqiang，He Qibo，et al. Empirical analysis on distribution system security region[J]. Automation of Electric Power Systems，2017，41(3)：153-160(in Chinese).

［12］ Yang Tiankai，Yu Yixin. Static voltage security region-based coordinated voltage control in smart distribution grids[J]. IEEE Transactions on Smart Grid，2018，9(6)：5494-5502.

［13］ 吴在军，胡靖宜，李培帅，等. 三相不平衡配电网不确定性分布式电源运行域仿射求解算法[J]. 电力系统自动化，2018，42(10)：67-74，149.

Wu Zaijun，Hu Jingyi，Li Peishuai，et al. Affine algorithm for solving dispatchable region of distributed generators with uncertainty in three-phase unbalanced distribution networks[J]. Automation of Electric Power Systems，2018，42(10)：67-74，149(in Chinese).

［14］ 肖 峻，苏步芸，贡晓旭，等. 基于馈线互联关系的配电网安全域模型[J]. 电力系统保护与控制，2015，43(20)：36-44.

Xiao Jun，Su Buyun，Gong Xiaoxu，et al. Model of distribution system security region based on interconnections of feeders[J]. Power System Protection and Control，2015，43(20)：36-44(in Chinese).

［15］ 肖 峻，贡晓旭，王成山，等. 智能配电网-1安全边界拓扑性质及边界算法[J]. 中国电机工程学报，2014，34(4)：545-554.

Xiao Jun，Gong Xiaoxu，Wang Chengshan，et al. Topology properties and algorithm of-1 security boundary for smart grid[J]. Proceedings of the CSEE，2014，34(4)：545-554(in Chinese).

［16］ 肖 峻，张宝强，张苗苗，等. 配电网安全边界的产生机理[J]. 中国电机工程学报，2017，37(20)：5922-5932.

Xiao Jun，Zhang Baoqiang，Zhang Miaomiao，et al. The formation of distribution network security boundaries[J]. Proceedings of the CSEE，2017，37(20)：5922-5932(in Chinese).

［17］ 李 京，刘道伟，安 军，等. 基于强化学习理论的静态电压稳定裕度评估[J]. 中国电机工程学报，2020，40(16)：5136-5148.

Li Jing，Liu Daowei，An Jun，et al. Static voltage stability margin assessment based on reinforcement learning theory[J]. Proceedings of the CSEE，2020，40(16)：5136-5148(in Chinese).

［18］ 刘 佳，程浩忠，李思韬，等. 兼顾供电能力和安全裕度的智能配电网协调运行优化方法[J]. 电网技术，2016，40(11)：3532-3538.

Liu Jia，Cheng Haozhong，Li Sitao，et al. Coordinated operation optimization method for smart distribution system considering total supply capability and security margin[J]. Power System Technology，2016，40(11)：3532-3538(in Chinese).

［19］ 刘 佳，程浩忠，李思韬，等. 考虑-1安全约束的分布式电源出力控制可视化方法[J]. 电力系统自动化，2016，40(11)：24-30.

Liu Jia，Cheng Haozhong，Li Sitao，et al. Visualization method of output power control of distributed generators considering-1 security constraint[J]. Automation of Electric Power Systems，2016，40(11)：24-30(in Chinese).

［20］ 刘 佳，程浩忠，徐 谦，等. 安全距离理论下计及故障恢复的智能配电网随机规划[J]. 电力系统自动化，2018，42(5)：64-71.

Liu Jia，Cheng Haozhong，Xu Qian，et al. Stochastic planning of smart distribution network based on security distance methodology considering fault recovery[J]. Automation of Electric Power Systems，2018，42(5)：64-71(in Chinese).

［21］ 江 钧，成乐祥，孙国强，等. 考虑安全域的配电网重构二阶锥双层规划模型[J]. 电力系统保护与控制，2019，47(4)：9-16.

Jiang Jun，Cheng Lexiang，Sun Guoqiang，et al. Distribution network reconfiguration based on second order cone bi-level programming considering security distance[J]. Power System Protection and Control，2019，47(4)：9-16(in Chinese).

［22］ 肖 晗，叶志浩，马 凡，等. 舰船直流区域配电系统安全运行边界计算与分析[J]. 电工技术学报，2016，31(20)：202-208.

Xiao Han，Ye Zhihao，Ma Fan，et al. Calculation and analysis of the safe operation boundary of shipboard DC zonal electric distribution system[J]. Transactions of China Electrotechnical Society，2016，31(20)：202-208(in Chinese).

［23］ 肖 晗，叶志浩，纪 锋. 考虑电动机启动的舰船直流区域配电系统最大供电能力计算与分析[J]. 中国电机工程学报，2017，37(18)：5228-5237.

Xiao Han，Ye Zhihao，Ji Feng. Analysis and calculation of total supply capability of vessel DC zonal electric distribution system during motor start-up[J]. Proceedings of the CSEE，2017，37(18)：5228-5237(in Chinese).

［24］ Chen Sheng，Wei Zhinong，Sun Guoqiang，et al. Convex hull based robust security region for electricity-gas integrated energy systems[J]. IEEE Transactions on Power Systems，2019，34(3)：1740-1748.

［25］ Su Jia，Chiang Hsiao-Dong，Zeng Yuan，et al. Toward complete characterization of the steady-state security region for the electricity-gas integrated energy system[J]. IEEE Transactions on Smart Grid，2021，12(4)：3004-3015.

［26］ Liu Liu，Wang Dan，Hou Kai，et al. Region model and application of regional integrated energy system security analysis[J]. Applied Energy，2020，260：114268.

［27］ Yong Pei，Wang Yi，Tomislav C，et al. Steady-state security region of energy hub：Modeling，calculation，and applications[J]. International Journal of Electrical Power & Energy Systems，2021，125：106551.

［28］ Wang Tao，Zhang Shang，Gu Xueping. A trend-based approach for situation awareness in power systems[J]. International Transactions on Electrical Energy Sys-tems，2017，27(12)：e2446.

［29］ 顾雪平，张 尚，王 涛，等. 安全域视角下的有功安全校正优化控制方法[J]. 电力系统自动化，2017，41(18)：17-24.

Gu Xueping，Zhang Shang，Wang Tao，et al. Optimization control strategy for active power correction from perspective of security region[J]. Automation of Electric Power Systems，2017，41(18)：17-24(in Chinese).

［30］ 肖 峻，肖居承，张黎元，等. 配电网的严格与非严格安全边界[J]. 电工技术学报，2019，34(12)：2637-2648.

Xiao Jun，Xiao Jucheng，Zhang Liyuan，et al. Strict and non-strict security boundary of distribution network [J]. Transactions of China Electrotechnical Society，2019，34(12)：2637-2648(in Chinese).

［31］ 肖 峻，左 磊，祖国强，等. 基于潮流计算的配电系统安全域模型[J]. 中国电机工程学报，2017，37(17)：4941-4949.

Xiao Jun，Zuo Lei，Zu Guoqiang，et al. Model of distribution system security region based on power flow[J]. Proceedings of the CSEE，2017，37(17)：4941-4949(in Chinese).

［32］ 肖 峻，甄国栋，王 博，等. 配电网的安全距离：定义与方法[J]. 中国电机工程学报，2017，37(10)：2840-2851.

Xiao Jun，Zhen Guodong，Wang Bo，et al. Security distance of distribution network：Definition and method [J]. Proceedings of the CSEE，2017，37(10)：2840-2851(in Chinese).

［33］ 陈思捷，陈启鑫，夏 清. 静态安全距离：概念，模型和意义[J]. 中国电机工程学报，2015，35(3)：600-608.

Chen Sijie，Chen Qixin，Xia Qing. Steady-state security distance：Concept，model and meaning[J]. Proceedings of the CSEE，2015，35(3)：600-608(in Chinese).

［34］ Chen Sijie，Chen Qixin，Xia Qing，et al.-1 security assessment approach based on the steady-state security distance[J]. IET Generation，Transmission & Distribution，2015，9(15)：2419-2426.

［35］ Chen Sijie，Chen Qixin，Xia Qing，et al. Steady-state security assessment method based on distance to security region boundaries[J]. IET Generation，Transmission & Distribution，2013，7(3)：288-297.

［36］ 肖 峻，林启思，左 磊，等. 有源配电网的安全距离与安全分析方法[J]. 电力系统自动化，2018，42(17)：76-86.

Xiao Jun，Lin Qisi，Zuo Lei，et al. Security distance and security analysis method for active distribution network[J]. Automation of Electric Power Systems，2018，42(17)：76-86(in Chinese).

［37］ Xiao Jun，Wang Chuanqi，She Buxin，et al. Total supply and accommodation capability curves for active distribution networks：Concept and model[J]. International Journal of Electrical Power & Energy Systems，2021，133：107279.

［38］ 肖 峻，曹 严，张宝强，等. 配电网安全域的全维直接观测[J]. 电工技术学报，2020，35(19)：4171-4182.

Xiao Jun，Cao Yan，Zhang Baoqiang，et al. Full-dimensional direct observation of distribution system se-curity region[J]. Transactions of China Electrotechnical Society，2020，35(19)：4171-4182(in Chinese).

［39］ 肖 峻，张宝强，邵经鹏，等. 配电网安全域的全维观测[J]. 电力系统自动化，2018，42(16)：73-79.

Xiao Jun，Zhang Baoqiang，Shao Jingpeng，et al. Full-dimensional observation of distribution system security region[J]. Automation of Electric Power Systems，2018，42(16)：73-79(in Chinese).

［40］ Allan R N，Billinton R，Sjarief I，et al. A reliability test system for educational purposes-basic distribution system data and results[J]. IEEE Transactions on Power Systems，1991，6(2)：813-820.

［41］ 马文蔚，解希顺. 物理学：中册[M]. 4版. 北京：高等教育出版社，1999：34-42.

Ma Wenwei，Xie Xishun. Physics：Part Ⅱ[M]. 4th ed. Beijing：Higher Education Press，1999：34-42 (in Chinese).

Security Distribution in the Operational State Space of Distribution Network：Characteristics and Application

Xiao Jun1，Jiao Heng1，Song Chenhui2，Qu Yuqing1

(1. Key Laboratory of Smart Grid of Ministry of Education(Tianjin University)，Tianjin 300072，China；2. State Grid Energy Research Institute Co.，Ltd.，Beijing 102209，China)

Owing to the construction of smart grids，the dispatching operation of urban distribution networks has become more intensive in China. Thus，it is necessary to deeply study the operational state space of a distribution network，especially the-1 security concerning the dispatching department. This paper discusses the security distribution in the operational state space of a distribution network for the first time. First，to establish the mapping relationship between the system states(operating points)and security analysis results，two security functions considering the capacity constraints of the subsation transformer are designed to quantify the security degree for systems. Second，the concept of state space security distribution is proposed. The security function values of all operating points in the state space constitute the state space security distribution. Third，the proposed concept and method are tested on an expanded IEEE RBTS-Bus4 case. This paper draws the state space security distribution of the test case for the first time. It is found that the security distribution in the state space forms a “security field”，similar to the natures of the electric and magnetic fields. The characteristics of security distribution are as follows：the security is centered on the no-load point and distributed in the form of “equal security lines” having the property of monotonic reduction. The farther the security is away from the center，the lower the line value. The normal direction of the equal security lines becomes that wherein the security changes most quickly and is the optimal control direction to improve security.

distribution network；operational state space；security distribution；security function

10.11784/tdxbz202201009

TM711

A

0493-2137(2023)02-0148-12

2022-01-11；

2022-04-22.

肖 峻（1971—  ），男，博士，教授，xiaojun@tju.edu.cn.

焦 衡，jiaoheng@tju.edu.cn.

国家自然科学基金资助项目(52177105).

Supported by the National Natural Science Foundation of China(No. 52177105).

(责任编辑：孙立华)