面向类别不平衡负荷序列模式识别的两阶段选择集成学习策略

王圆圆，韩 丁，王世谦，白宏坤，王 磊，刘 洋

（1.国网河南省电力公司经济技术研究院，郑州 450052；2.四川大学电气工程学院，成都 610065）

伴随智能电网和能源互联网的发展，人工智能技术与传统电网技术的日益融合，成为电网管理者快速感知电力系统多源数据规律、实施精准控制和决策的重要辅助手段[1-4]。当前，集成学习和神经网络等人工智能理论在电力用户负荷模式识别中已受到广泛重视，其对电网企业开展精细化用户用电行为建模、制定个性化用电服务及提升企业市场竞争力具有重要价值[5-8]。

集成学习因具有良好的算法稳定性、准确度增益和算法普适性被引入计算机视觉、生物、医学及工程等多个学科领域。近年来，集成学习在电力负荷模式识别领域的研究中备受重视。负荷模式直观表现为负荷时间序列的曲线形态和时段负荷水平，它反映了用户该时间尺度下的用电行为规律。负荷模式是精细化开展用电行为画像、辨识需求响应潜力用户的理论基础[9-11]，文献[12]结合负荷序列的时域和频域特征，构建基于长短期记忆LSTM（long short-term memory）神经网络的日负荷模式辨识及提取算法；文献[13]针对传统K-means聚类方法中聚类结果稳定性差和距离度量不能反映负荷曲线趋势相似度的问题，提出一种基于中心优化和双尺度相似性度量的负荷聚类式分类方法。随着智能仪表的普及应用，用户级负荷数据大量累积，海量用户负荷数据高性能处理成为重要研究课题。针对大规模负荷数据的分类效率问题，文献[14-15]提出结合自动编码器特征降维和无监督聚类的负荷分类方法；文献[16]提出一种分布式并行LSTM神经网络负荷模式识别模型，将负荷数据切分为样本规模更小的子块存放在分布式文件存储系统中，在各个计算节点完成负荷分类任务；文献[17-18]为解决数据分块带来的分类精度下降问题，基于Hadoop大数据计算平台，提出分布式并行集成反向传播神经网络BPNN（back propagation neural network）的负荷模式分类方法，采用Bagging式集成学习对各子计算节点部署的基分类器进行融合决策，弥补子节点分类器的精度损失。以Bagging为代表的并行式集成学习与负荷数据分布式处理具有良好的算法适配性，成为提升用户侧大数据处理效能的重要方法，但相关研究均未考虑集成学习广泛存在的基分类器冗余问题。当基分类器集群陷入同质化时，基分类器便失去差异性，集成学习就会失效且增加无效数据处理成本[19]。目前，基分类器集成的经典方法包括异质基分类器集成、随机子空间集成和Boosting、Bagging集成等[20]。异质基分类器集成对基分类器的选择缺乏通用标准；随机子空间集成面临特征子空间冗余的类似问题；Boosting集成易受数据噪声影响，算法鲁棒性差，且为串行式算法逻辑，对大量负荷数据的处理存在效率缺陷；Bagging集成鲁棒性较强，与主流的分布式计算框架具有良好的适配性，但基分类器冗余问题严重。选择集成策略是应对Bagging集成学习中基分类器冗余的有效方法[21]，其选择部分性能优越的基分类器参与集成，可获得效率提升和同等甚至更高的性能增益。

伴随智能电表的广泛应用，用户负荷数据体量和用电行为复杂性均不断提升[22-23]，负荷样本潜在的类别不平衡问题增强，增加了精准分类的难度[24-25]。类别不平衡表现为分类模型中少数类样本的辨识度被多数类淹没，是电力数据模式分类领域的重要难题之一。少数类样本过采样技术是解决类别不平衡问题的有效方法，文献[26]采用生成对抗网络合成窃电监测样本，克服少数类样本数目不足的问题。深度学习模型通过学习样本分布规律能获取较高质量的新样本，但算法复杂且需要大量数据资源驱动。文献[17]引入基于k-近邻采样原理的合成少数类过采样技术SMOTE（synthetic minority over-sampling technique），有效提升了少数类负荷样本的分类精度；文献[18]针对SMOTE算法近邻样本选择盲目的问题，采用边界合成少数类过采样技术BSMOTE（borderline synthetic minority over-sampling technique）加以改善。上述SMOTE方法均未考虑少数类样本的密度分布特性，采样过程与类别重叠现象的耦合作用也会削弱分类模型的泛化性能。

本文为解决集成学习负荷模式识别中的类别不平衡及基分类器冗余等问题，提出一种计及类别平衡的两阶段选择集成学习TSSEL（two stage selective ensemble learning）电力负荷序列模式识别方法。采用一种基于密度聚类的高斯合成少数类样本过采样技术DCB-GSMOTE（density clusteringbased Gaussian synthetic minority over-sampling technique），解决少数类负荷样本在模式识别任务中被多数类淹没的问题。同时，设计一种包括基分类器聚类剪枝及优化集成的两阶段选择集成负荷分类模型。

1 类别不平衡处理

1.1 DCB-GSMOTE算法基本概念

DCB-GSMOTE根据少数类样本集的密度分布特性进行自适应人工样本合成采样，其对样本集的密度分布表征借鉴DBSCAN（density-based spatial clustering of applications with noise）算法的直接密度可达图理念涉及的相关基本概念如下。

（1）ρ-邻域。已知一聚类簇Z，设其中一样本xi的邻域半径为ρ，定义xi的ρ-邻域Nρ(xi)为

（2）核心点。已知样本xi，若其ρ-邻域Nρ(xi)内至少存在κ个样本点，则称xi为核心点。

（3）直接密度可达。已知样本xi、xj，若xi为核心点，且满足xj∈Nρ(xi)，则称xj对xi直接密度可达。

（4）直接密度可达图。设V是Z中所有满足直接密度可达条件的样本集合，将直接密度可达样本对的加权图路径定义为直接密度可达边，路径权重表征为样本对的欧式距离；设E为Z中所有直接密度可达边的集合，称G(Z,ρ,κ)=(V,E)为聚类簇Z在ρ和κ参数条件下的直接密度可达图。

1.2 DCB-GSMOTE算法基本流程

步骤1判别少数类日负荷序列样本。已知日负荷标签样本集D，按负荷模式类别差异划分为M类样本子集{Dm|m=1,…,M}。若样本子集Dm的样本数量小于最大样本子集数量的1/5，则判定该类负荷样本子集为少数类，对其进行样本合成。

步骤2少数类样本密度聚类。设Dm为少数类样本集，对其实施DBSCAN聚类，得到若干聚类簇{Dm,c|c=1,…,C}，其中，Dm,c为第c个聚类簇，C为聚类簇总数。记录各聚类簇的聚类中心样本。

步骤3聚类簇构建直接密度可达图。记录DBSCAN聚类后每个聚类簇Dm,c的直接密度可达图G(Dm,c,ρ,κ)。

步骤4确定每一聚类簇Dm,c的样本合成数目。计算各聚类簇的样本数目分布比例，按比例在各聚类簇中合成新样本。

步骤5采样路径搜索。每次合成新样本时在Dm,c随机选定一真实样本xr，在G(Dm,c,ρ,κ)中采用Dijkstra算法搜索xr到聚类中心xcenterc的最短加权图路径，其中，为xr到最短加权图路径经过的样本点，↔为直接密度可达。将Jr↔center作为本次的采样路径。

步骤6新样本合成。在Jr↔center中随机选择一段直接密度可达边作为本次的采样区间。

在采样区间内设定插值距离l，其服从的均匀分布可表示为

随机生成插值坐标q为

为增强合成样本的多样性，对q添加一随机扰动向量o。o的每一维度均服从的正态分布为

式中，σ为相对标准差。

最后生成本次的新样本xsynthetic为

步骤7重复步骤5、6，直到少数类样本总数目达到最大样本子集数目的1/5。

2 负荷模式识别的两阶段选择集成策略

集成学习中基分类器的差异性和准确率是影响集成性能的关键因素，其中，差异性是指基分类器对样本做出不同错分的趋势，差异性和准确率高的基分类器集群可以获得更好的集成增益。兼顾基分类器的差异性和识别准确率，提出基于差异性模糊增量的聚类剪枝策略CBPS（clustering-based pruning strategy）和基于正则化代理集成分类精度损失的优化选择集成OBSI（optimization-based selection integration）策略的两阶段选择集成负荷模式识别方法。

2.1 CBPS策略

所提基于差异性模糊增量DFI（diversity fuzzy increment）的CBPS首先构建基分类器的DFI特征向量，基于DFI特征向量采用近邻传播AP（affinity propagation）聚类将基分类器集群划分为若干类，剪枝除聚类中心外的其余冗余基分类器个体。同时，为确定基分类器池的最佳聚类剪枝数目，提出基于欧式冗余度和余弦冗余度双度量指标的基分类器集群冗余度评价方法。

2.1.1 DFI特征向量

采用Q-统计量构建基分类器的DFI特征向量，该指标隶属成对差异性度量的范畴，用于度量两基分类器之间的决策差异性[27]。第m类负荷样本分类任务中基分类器u和基分类器v的Q-统计量可表示为

式中：au,v、du,v分别为基分类器u和v对训练样本集作出＜正确，正确＞、＜错误，错误＞分类的概率；bu,v、cu,v分别为基分类器u和v对训练样本做出＜正确，错误＞、＜错误，正确＞分类结果的概率[21]。

表1为au,v、bu,v、cu,v和du,v服从的联合分布，其中，hu(xk)、hv(xk)分别为基分类器u和v对训练样本xk的分类结果；yk为xk的类别标签。

表1 两基分类器间的联合分布Tab.1 Joint distribution for two base classifiers

基于Q-统计量，构建基分类器集群的整体差异性指标φm为

式中，L为基分类器数目。

为描述基分类器个体对集群整体差异性变化的影响，定义第m类训练样本中基分类器u的DFI为Eu,m，其公式可表示为

式中，Ωu⊄Ω、Ωu⊂Ω分别为包含和不包含基分类器u的基分类器集合。

设样本总类别数为M，分别计算不同类别对应的差异性模糊增量，构建基分类器集群的DFI特征矩阵E为

2.1.2 基分类器集群最佳聚类中心数目评估

欧氏距离和余弦距离常用于数据序列的相似性评估。对基分类器集群完成一次聚类后，计算所有聚类中心的基分类器子集DFI特征向量的平均欧氏距离和余弦距离，欧式冗余度指标ERI（European redundancy index）IERI和余弦冗余度指标CRI（cosine redundancy index）ICRI可表示为

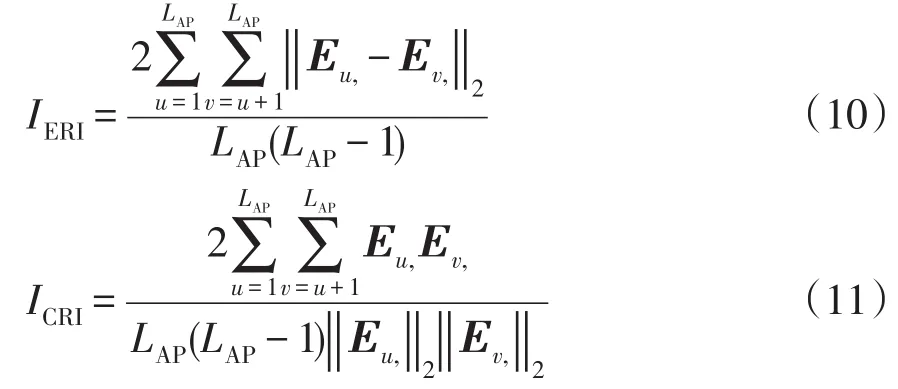
式中：LAP为基分类器聚类中心的数目；Eu,、Ev,分别为DFI特征矩阵E的第u和v行向量。IERI越大或者ICRI越小意味聚类中心基分类器子集的平均差异性越大，基分类器冗余度越低。聚类时将IERI和ICRI取最值时的聚类中心数目Lmost作为最佳剪枝结果。

2.1.3 CBPS算法基本流程

步骤1基分类器池生成。已知日负荷标签样本集D，抽样训练生成L个基分类器，构成原始基分类器池。

步骤2DFI特征向量构建。根据D计算基分类器池中所有基分类器对的Q-统计量，进而生成所有基分类器的DFI特征向量集合，构建DFI特征矩阵E。

步骤3基分类器集群聚类。设定偏好度参数，采用AP聚类算法对E矩阵行向量完成一次聚类，确定本次聚类的聚类中心数目。

步骤4基分类器集群聚类剪枝。按照步骤3完成多次聚类，直到选定ERI和CRI特性曲线的拐点。根据拐点聚类结果，将所有聚类中心对应的基分类器作为CBPS去冗余的基分类器集合。

2.2 OBSI策略

为提升选择集成模型的泛化能力，将OBSI策略引入集成边界的概念，构建最小正则化代理集成精度损失函数优化基分类器集成参与权重。

2.2.1 考虑模型复杂度的最大化Margin集成策略

集成边界最早由Schapire提出，是一种描述样本正确分类倾向程度的度量。已知负荷标签样本验证集Dverify={(xn,yn)|n=1,…,N}，其中，xn、yn分别为第n个样本和类别标签；设经CBPS策略剪枝得到基分类器集合为ΩCBPS，H(X)={hu(xn)|xn⊂Dverify;u⊂ΩCBPS}为ΩCBPS对Dverify的分类结果集合。则ΩCBPS对样本xn的集成边界Υ(xn,yn)可表示为

式中：υu为基分类器u的集成参与权重；ς(xn)为基分类器集成分类结果。若分类正确，则ynς(xn)=1；反之，ynς(xn)=-1。

基于集成边界，定义集成学习分类精度损失为

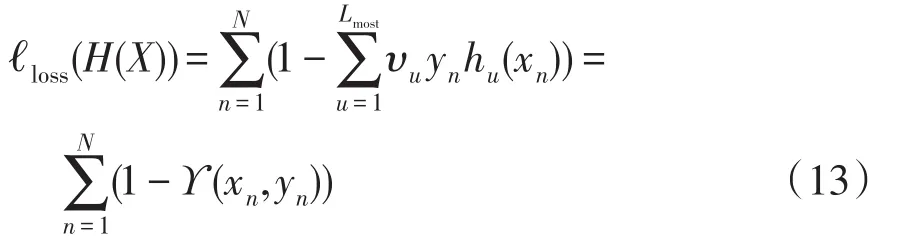
优化集成通过最小化集成精度损失，提升集成模型的泛化能力。为控制集成复杂度、抑制优化带来的集成过拟合问题，添加基于基分类器集成参与权重的正则项，构建的优化问题可表示为

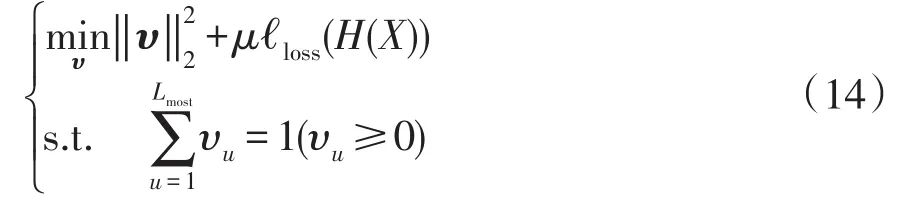
式中，μ为正则项和集成损失项的平衡因子，用于控制模型复杂度，υ=(υ1…υu…υLmost)；。

2.2.2 基于Huber函数的代理损失优化集成

由于所提集成学习分类精度损失函数ℓloss(H(X))属于非凸、不连续的目标函数，代理损失优化可有效改善其优化过程。采用截断Huber函数作为代理损失函数，引入参因子e来调节代理损失函数对异常值和噪声数据的敏感度，增强优化结果的鲁棒性和稳定性，本文设定为0.6。截断Huber函数可表示为

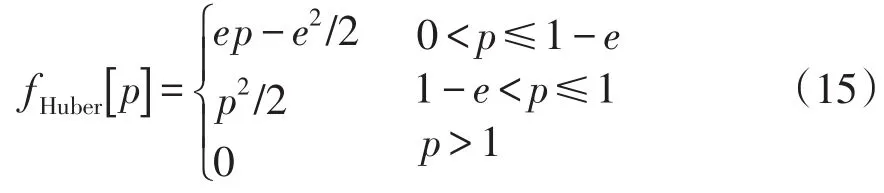
式中，p为集成学习分类的精度损失。

基于Huber代理损失函数的最小正则化代理集成分类精度损失函数可表示为

2.2.3 基于K折交叉验证的基分类器选择

采用K折交叉验证法从原始标签样本训练集中获得K个验证集Dverify，重复OBSI策略，获得K次ΩCBPS集成参与权重优化结果，记为Λ

式中，υs,u为第s次OBSI策略求解中第u个基分类器的集成参与权重。

将ΩCBPS中基分类器u的K次集成参与权重记为(υ1,u…υs,u…υK,u)，计算权重大于0的次数占比Ru为

式中，符号函数sign(·)在自变量大于0时取值为1，反之为-1。当Ru≥0.5时，该基分类器予以保留，采用多数投票法参与集成学习负荷模式识别任务。

2.3 所提负荷模式识别算法总体流程

本文所提负荷模式识别算法总体流程如下。

步骤1已知日负荷标签样本集D，将其按照类别划分为M个样本子集{Dm|m=1,…,M}，对每类样本子集按照比例4：6随机划分为训练子集Dtrain,m和测试子集Dtest,m两部分，对Dtrain,m的少数类样本进行DCB-GSMOTE类别平衡处理得到，合并各类样本子训练集及测试集分别得到训练样本集和测试样本集Dtest。

步骤2对采用Bootstrap重抽样提取L个同等规模的负荷标签样本子集，前向输入L个待训练的基分类器（以BPNN为例），采用Adam优化求解各自的目标损失函数（本文采用交叉熵损失函数），通过早停法确定学习次数，训练生成L个基分类器，构成基分类器集合Ω。

步骤3计算并记录Ω中每个基分类器对的分类结果，将其记为。基于Htrain(X)，根据式（6）～（9）构建基分类器的DFI特征矩阵E。

步骤4CBPS阶段，采用AP算法对E中所有基分类器的DFI特征向量进行聚类，根据式（10）、（11）确定基分类器池聚类剪枝的最佳保留数目LAP，将保留的基分类器集合记为ΩCBPS。

步骤5OBSI阶段，采用K折交叉验证，首先将按照各类样本的比例随机划分为K等份记为。

步骤6计算并记录ΩCBPS中每个基分类器对Dverify,s的分类结果，记为Htest(X)={hu(xk)|xk⊂Dverify,s;u⊂ΩCBPS}。根据式（12）～（16）计算ΩCBPS中基分类器的集成参与权重。

步骤7重复步骤6共K次，根据公式（17）计算得到K次基分类器集成参与权重Λ。

步骤8针对ΩCBPS中每个基分类器，以基分类器u为例，根据式（18），计算其K次集成参与权重大于0的次数占比Ru，若Ru≥0.5则予以保留，采用多数投票法参与集成学习负荷模式识别任务，完成对负荷标签样本集Dtest的分类。

3 算例验证

3.1 数据来源

算例所用数据来自UCI数据平台，包括电力系统暂态稳定模拟数据集EGSSDS（Electrical Grid Stability Simulated Data Set）和电力用户日负荷数据集Electricity Load Diagrams 20112014 Data Set（ELDDS）两种。EGSSDS自带标签信息，ELDDS所需日负荷样本类别标签参考文献[17]通过K-means及K-medoids聚类优选得到。数据集的基本信息如表2所示。

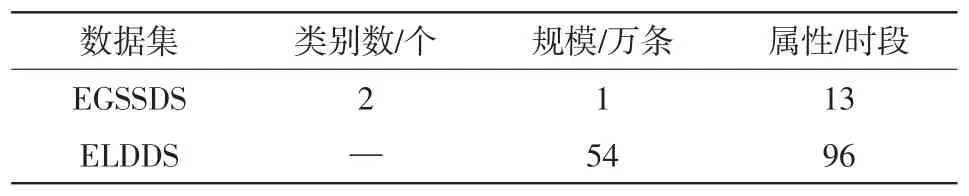
表2 数据集基本信息Tab.2 Basic information of data sets

3.2 分类效果评价指标

在二分类场景中，评估指标除采用分类准确率Acc以外，引入召回率Pre、查准率Ppr、Gmeans、Fvalue4种二分类评估指标[24]。其中，Pre为少数类样本中被正确分类的占比；Ppr为划分为少数类别的样本中少数类的真实占比；Gmeans为所有多数类和所有少数类正确分类占比的几何平均值，可以反映分类器对各类别的偏向程度，该值越接近全部样本的分类准确率Acc表明类别平衡效果越好；Fvalue为Pre、Ppr的调和平均值，该值越大表明算法在提升少数类分类精度时对多数类分类结果的影响越小。

在多类别分类场景中，混淆矩阵是评估分类性能的重要方法，但混淆矩阵难以定量描述算法对负荷类别的混淆均衡程度。因此，基于混淆矩阵提出类别混淆均衡熵指标。

二分类的混淆矩阵Mconfusion可表示为

式中：NTP、NTN分别为正确分类成为正类和负类的样本数；NFP、NFN分别为错误分类成为正类和负类的样本数。

在多类别分类场景下的混淆矩阵可以视为多个二分类混淆矩阵的组合，即将待研究类别看作正类，其余类别统归为负类。定义第m类样本为正类时的二分类调和平均准确率Γm为

Γm可以度量在二分类场景下的类别混淆程度，类别混淆越严重，Γm值越低。在此基础上，定义类别混淆均衡熵Sb为

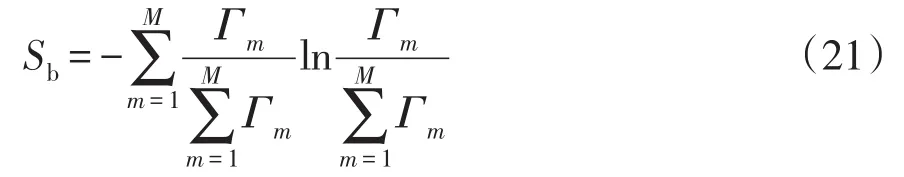
Sb值越大，表示分类模型对负荷各类别的混淆程度越均衡，同时表明过采样算法类别平衡效果越好。

3.3 DCB-GSMOTE算法性能验证

为验证DCB-GSMOTE算法的有效性，分别开展EGSSDS二分类和ELDDS多类别负荷分类实验。

3.3.1 EGSSDS暂稳数据集分类测试

由EGSSDS中随机抽取暂态不稳定和暂态稳定数据各2 000条作为验证集，再分别抽取4 000条和400条数据作为训练集。对比经过DCB-GSMOTE算法平衡处理和其他算法（包括SMOTE和BSMOTE，其中BSMOTE在下文中简写作BS）处理后样本在BPNN分类模型中的分类效果，实验结果如表3所示。

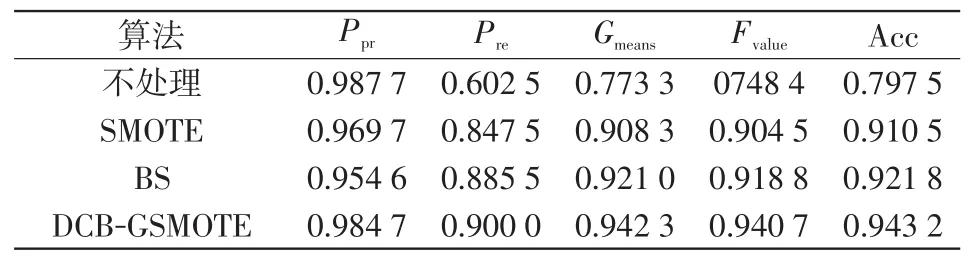
表3 EGSSDS二分类结果Tab.3 Binary classification results of EGSSDS

由表3结果可知，类别不平衡问题不作处理时，由于少数类样本训练不足容易错分，导致Ppr很高但Pre很低，EGSSDS整体分类精度较低；经过各类别平衡算法处理后，EGSSDS分类性能均有明显的提升。其中，DCB-GSMOTE各项分类评估指标均为最高，其Gmeans与Acc差值为0.09%，而SMOTE和BS分别为0.22%、0.08%，平均来看，类别平衡效果相对更好；同时，DCB-GSMOTE的Fvalue比SMOTE和BS分别高出3.62%和2.19%，算法对多数类样本的分类结果影响最小，性能更佳。在各项评估指标对比中，DCB-GSMOTE多优于SMOTE和BS算法，且各项分类评估指标值更为均衡，这表明DCB-GSMOTE算法具备更好的综合性能。

3.3.2 ELDDS负荷数据集分类测试

为对比测试DCB-GSMOTE算法的鲁棒性，对比测试不同高斯噪声含量下ELDDS负荷数据集的多类别分类结果。在开展ELDDS负荷分类实验之前，根据文献[17]中K-means、K-medoids聚类算法组合获取负荷样本的类别标签，截断选取接近各聚类中心的负荷标签样本，构成日负荷标签样本集D。D包括5类日负荷样本，共计16 620条负荷曲线，各类日负荷曲线的典型用电模式如图1所示。

图1 各类负荷曲线典型模式Fig.1 Typical modes of various load curves

将D按4：6的比例切分为原训练样本集Dtrain和测试样本集Dtest。各类训练集负荷样本数量为3 770：1 502：284：320：818（判定第3、4类为少数类负荷标签样本），对Dtrain中的少数类样本进行类别平衡处理，获得样本增强的训练样本集。同样选择BPNN为分类器训练并测试ELDDS负荷分类效果，实验结果如图2所示。

图2 不同噪声含量下算法准确率和Sb对比Fig.2 Comparison of accuracy andSbamong algorithms under different noise levels

在低噪声场景下，各算法性能基本持平。随着样本集噪声含量的增加，尤其达到0.9以后，经BS和SMOTE算法处理的ELDDS负荷分类准确率Acc和类别混淆均衡熵Sb均显著减小，而DCBGSMOTE的 Acc和Sb下降不明显，相较BS和SMOTE表现出更优的稳健性和抗噪性，算法鲁棒性更强。

3.4 TSSEL算法性能验证

3.4.1 实验过程参数配置

为测试所提TSSEL策略的有效性，本节实验选取3种机器学习分类模型作为参与集成学习的基分类器，分别为BPNN、决策树CART（Classification and Regression Tree）及LSTM神经网络。首先，以BPNN为基分类器，根据第2.3节步骤2，通过Bootstrap算法从重复抽取与训练集同等规模的负荷标签样本子集100个，训练分类器模型生成BPNN基分类器池，集群规模为100个；根据第2.3节步骤3，基于构建基分类器集群的DFI特征矩阵E；根据第2.3节步骤4，通过CBPS算法剪枝得到去冗余基分类器集合。图3为基分类器集群ERI和CRI的分布特性，由图3可知，基分类器集群规模LAP达到37时，冗余度指标IERI和ICRI达到最值，保留此时所有聚类中心的基分类器构成集合ΩCBPS，完成第一阶段选择集成。

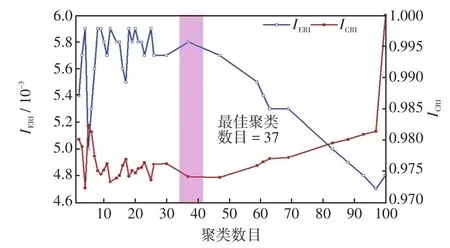
图3 基分类器集群ERI和CRI分布特性Fig.3 Distribution characteristics of ERI and CRI of base classifiers

基于去冗余的基分类器集群ΩCBPS，开展第2阶段选择集成实验。为确定超参数μ的合理取值，μ取值范围从0.001～100按指数级变化，根据第2.3节步骤6，计算OBSI策略的优化结果υ，得到υ*-μ特性曲线簇如图4所示，图4的每根折线表示ΩCBPS中每个基分类器的υ*-μ特性曲线。当平衡因子μ达到1时，各基分类器的集成参与权重系数υ*刚趋于稳定。选择此时的μ值在满足集成精度要求的同时，可抑制集成负荷分类模型的过拟合问题。

图4 基分类器υ*-μ特性曲线簇Fig.4 υ*-μcharacteristic curve cluster of base classifiers

3.4.2 ELDDS负荷分类性能测试

根据第2.3节步骤5～7，采用5折交叉验证，重复步骤5共5次，计算每次的ΩCBPS集成参与权重，获得集成参与权重矩阵Λ。根据第2.3节步骤8得到OBSI策略保留的基分类器集合，共计9个基分类器，通过多数投票法参与Dtest的负荷分类任务。

将BPNN、CART和LSTM分别作为基分类器实施DCB-GSMOTE类别平衡及两阶段选择集成，同时基于ELDDS数据集对比基分类器采用不同集成策略时（无类别平衡处理）的负荷分类效果。Dtest的负荷分类准确率Acc及类别混淆均衡熵Sb分别如表4和表5所示。

表4 不同算法分类Acc对比Tab.4 Comparison of classification accuracy among various algorithms

表5 不同算法Sb对比Tab.5 comparison ofSbamong various algorithms

在表4和表5中，本文所提计及类别平衡的TSSEL负荷模式识别策略，较Bagging、Adaboost集成表现出更高的分类准确率Acc和类别混淆均衡熵Sb。通过3种不同的基分类器（BPNN、CART和LSTM）集成负荷分类实验验证了所提方法具备一定普适性。实验结果表明，通过TSSEL选择集成策略遴选差异化强、准确率高的基分类器参与负荷分类任务的组合决策，可以在保证负荷分类效果的同时，有效降低集成学习的算法规模。

3.4.3 算法稳定性测试

为验证所提TSSEL策略算法的稳定性，以BPNN为基分类器，对比TSSEL、Bagging集成学习BEL（bagging ensemble learning）在多次重复实验中对ELDDS测试集Dtest的分类准确率波动情况。其中，BEL的基分类器数目分两种来对照测试（L和LTSSEL，即100和9）。各集成BPNN分类模型训练所需的负荷标签样本集均采用经过DCB-GSMOTE类别平衡后的。各集成BPNN算法的缩写名称分别记为：TSSEL-BPNN(LTSSEL)、BEL-BPNN(LTSSEL)和BEL-BPNN(L)。实验重复300次，结果如图5所示。

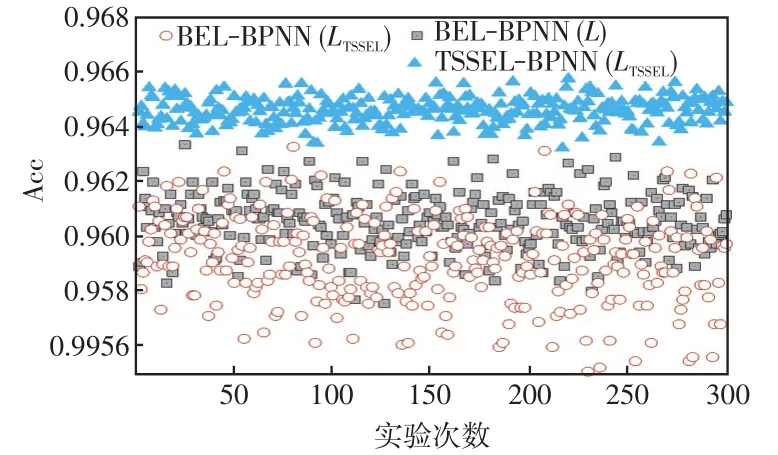
图5 TSSEL算法的稳定性测试Fig.5 Stability test of TSSEL algorithm

在图5中，TSSEL-BPNN分类正确率主要分布于区间[0.964，0.966]之间；BEL-BPNN（L）分类正确率主要分布于区间[0.958，0.962]之间；BEL-BPNN(LTSSEL)分类正确率主要分布于区间[0.956，0.961]之间。BEL-BPNN（L）分类正确率的分布区间比BEEBPNN(LTSSEL)减小20%，表明提升基分类器的集成规模可以增强BEL-BPNN的分类稳定性。本文所提TSSEL-BPNN分类准确率的分布区间比BELBPNN(LTSSEL)减小60%，减小量较BEL-BPNN（L）提高40%，这表明基学习机池中冗余基分类器不仅对样本分类准确率有影响，也会降低集成分类算法的稳定性，因此，所提TSSEL策略可有效提升负荷分类算法的稳定性。

4 结论

针对集成学习负荷模式识别中的类别不平衡问题及基分类器冗余问题，提出一种计及类别平衡的TSSEL电力负荷序列模式识别方法。通过算例分析论证得出以下结论。

（1）DCB-GSMOTE类别平衡算法能根据负荷样本的密度分布特性实施过采样，较SMOTE和BS算法具有更好的负荷类别平衡效果和算法鲁棒性，可有效抑制类别不平衡问题导致的少数类负荷样本辨识度被多数类淹没的问题。

（2）面向负荷模式识别的TSSEL策略，通过CBPS和OBSI策略缩减基分类器池规模，可有效改善基分类器冗余问题对负荷分类精度集成增益的影响，同时可增强负荷分类模型的算法稳定性。

（3）采用DCB-GSMOTE算法和TSSEL策略的负荷模式识别算法，从数据层和算法层分别解决类别不平衡问题和基分类器冗余问题对负荷模式识别性能的影响，较传统Bagging、Adaboost集成能取得更优的分类精度，且算法框架具有一定普适性，为电力用户负荷数据高性能处理提供了有价值的研究思路，对开展用户多层级需求响应潜力画像及用户侧需求响应资源聚合评估研究具有参考价值。