高中数学导数教学中分类讨论法的应用

2023-02-11荣荟翠

新课程 2023年22期

文| 荣荟翠

教师对导数教学的各方面内容进行分类讨论，可以帮助学生了解导数基础知识，让学生高效地掌握导数内涵，并灵活解决导数问题。

一、简化解题步骤

从近些年的高考题中我们不难看出“导数”已经成为重点考查的内容，利用导数求函数的最值问题是常见的题型。在解答此类导数问题时，就可应用分类讨论法对题目进行分析，通过分类与逐层分析，可以让解题过程更加简单，且能让学生的解题步骤更加清晰、明确，对于知识的掌握也会更加深入。在应用分类讨论法的过程中，学生可以逐步明确函数的性质，掌握问题的本质。在具体的应用过程中，教师需以具体的题型为引导，让学生针对性地进行分析与讨论，通过化整为零的方式进行分类，降低问题的难度。一般情况下，函数f（x）在区间［a，b］上可导，那么f（x）在区间［a，b］上最值的求法有以下三种：（1）求出f（x）在区间［a，b］上的极值；（2）计算f（x）在极值点和端点的函数值；（3）对f（x）极值点和端点的函数值进行比较，写出最大值、最小值。

案例一：已知函数f（x）=x3-3x，求函数在区间［-3，2］的最大值和最小值。

解析：由题中f（x）=x3-3x可以得出f′（x）=3x2-3=3（x+1）（x-1），则当x∈（1，2］时，f（x）＞0，所以［-3，-1］，［1，2］是函数f（x）的单调增区间，当x∈［1，1］时，函数f′（x）＞0，所以可知［-1，1］是函数f（x）的单调减区间。

又因f（-3）=-18，f（-1）=2，f（1）=-2，当x=-3时，f（x）取得最小值，为-18，当x=-1 或者2时，f（x）取得最大值，为2。

二、解决导数零点问题

导数是学习高等数学知识的基础，以导数为基础的各种函数问题成为重点学习的内容。在求解导数题目的过程中我们发现，题目中常包含多种参数，随着参数的改变，解题的难度也会增加，所以通过分类讨论的方式进行答题非常关键。而在利用导数求函数单调性的问题中，我们重点需要考虑的问题就是函数的零点问题，解决此类问题需要考虑的重点就是二次项系数中是否含有参数，当参数是“0”时，就需要将函数转化成一次函数进行判断，如果参数不为“0”时，就需要对导函数进行因式分解，并判断，如果可以则表示存在零点。在讨论零点问题的过程中，判断正负非常关键，零点是正负的临界点，会影响整个解题结果。针对导数函数的零点案例，对学生进行分类讨论训练非常有必要，教师需针对具体的问题进行多样化训练，逐步提高学生的解题能力。

案例二：已知函数（fx）=x-blnx，（fx）有几个零点？

解析：根据题干信息，（fx）=x-blnx，x＞0 则可以得出，如果令g（x）=x2-bx+1，Δ=b2-4；则可以得出下列结果：

1.当-2≤b≤2 时，g（x）≥0，当x＞0 时，f′（x）＞0是恒成立的，那么f（x）就会单调递增。又因f′（1）=0，所以这时函数只有一个零点。

2.当b＜-2 时，g（x）=0，此时函数会有两个不等的实根，假设这两个实根分别为x1，x2，那么根据根和系数的关系就可得到下列关系式x1+x2=b＜0，x1、x2=1，则x1＜0，x2＜0，当x＞0 时f′（x）＞0，恒成立，且此时函数f（x）只有一个零点。

3.当b＞2 时，g（x）=0 有两个不相等的实数根，假设这两个实根分别为x1、x2，则当x1+x2=b＞0，x1x2=1，如果设0＜x1＜1＜x2；

则当0＜x＜x1时，f′（x）＜0，f（x）是单调递增；

当x1＜x＜x2时，f′（x）＜0，f（x）是单调递减；

当x＞x2时，f′（x）＜0，f（x）是单调递增；

f（x1）＞f（1）=0＞f（x2）

当b≤2 时，f（x）有一个零点，而当b＞2 时，f（x）有三个零点，所以最终的答案是“f（x）有三个或者一个零点”。

三、命题等价转换

在转换的过程中，需落实“等价”原则，面对千变万化的数学问题，须知“万变不离其宗”，要想更加准确地解答数学题目，在烦琐的题干信息中筛选出有效信息，就需对题目信息进行分类讨论，善于观察和联想，对复杂的数学问题进行归类转化，让问题更加简单，学生的解答也更加顺利。

案例三：已知函数f（x）=ax2-lnx（a是常数），如果a＜0，那么在任意情况下x∈［1，e］，f（x）≥（a-2）x恒成立，求实数a的取值范围。

解析1：利用分类讨论中的构造法，整合出一个新的函数，再进行求导。新函数为F（x）=f（x）-（a-2）x，由此就可将上述问题转换成“对任意x∈［1，e］，F（x）≥0恒成立”进一步进行转化，就可得到F（x）min≥0，围绕F（x）min这一核心问题，通过分类讨论就可得到参数a的取值范围。

解析2：可将函数中的参数a单独剥离，这样就可得到分离之后函数的最值，一般情况下处理恒成立的主要方式就是通过分类讨论的方式得到最值，然后再解答不等式得到答案，再通过分离参数函数的具体情况进行讨论。

以上的两种解题思路都与分类讨论密切相关，解析1 应用了构造法，通过对构造函数F（x）min的参数a进行分类讨论，得到最终结果。在此处进行分类讨论的主要原因就是当F′（x）=0 时的其中一个根-是否在定义域内，是否要大于另一个根。而解析2 中主要是对变量进行分类讨论，主要是当参数为a，不能确定函数系数x2-x的值是正、负，还是零。由此可见，以上两种方法均需要应用分类讨论法的主要原因，就是结果存在不确定性，对于数值的大小、正负均无法确定。

四、数形结合直观反映

从导数、函数的实际教学情况来看，很多高中生面对此类题目，时常不知所措，心存畏惧。而教师也与学生有一样的感觉，在教学中也深感无所适从，不知从何角度能帮助学生更好地理解导数问题。导数之所以难教、难学，我认为有两方面原因：一方面是导数对学生来讲属于一个新词，有一种陌生感；同时，教师并未过多地讲解过导数，猛然间提及导数，学生就会感到一脸茫然，不知所措。另一方面在于导数是“数”与“形”之间的相互融合，与以往单一形式的“数”的教学与“形”的教学有一定差异，由此产生对导数教学的两种错误认识。首先，部分教师仅将导数作为一门独立学科对待，仅重视代数教学而忽视图形教学；其次，教师也认为导数、函数分析的重点是图形，仅关注图形而忽视代数教学。从常识角度来看，不管是导数，还是函数，都是“图形”与“代数”相结合的桥梁，且存在于数学教学的整个过程中。因此，数形结合法是分类讨论的有效手段之一，可以让学生对知识有更清楚的认识，并且在图形的支持下，数量之间的关系也更加明朗。函数教学之前，教师应确保学生对函数有正确的理解，并能够对函数本质有清晰认识，即函数是一种对应关系，主要体现在量与量之间。

案例四：已知函数（fx）=+alnx，a∈R，此函数需过点（0，2），那么过此点的函数可以作几条与函数y=f（x）相切的直线，为什么？

解析：本题目的答案为a≤0 时，有一条切线，a＞0 时有两条切线，理由如下：

假设将切点坐标设为［x0，f（x0）］，根据题意就可得到即可得到对算式进行化简就可以得到假设可以得到函数F（x）在（0，+∞）区间上的零点数量，也就是相切曲线的数量。而结合F（x）的性质可以得到图象有以下几种情况：

对图1 中的图象进行观察，只要分类讨论x=1时是否穿过了x轴，就可对交点情况进行逐一验证。

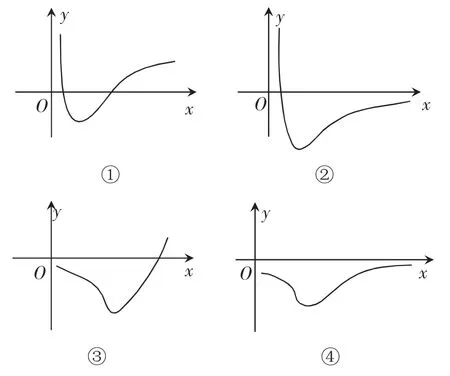
图1

五、精准定位问题特征

在分类讨论时，教师应引导学生找到分类讨论的正确依据，明确分类讨论的原因、引起分类讨论的因素、采取分类讨论的合理方法。学生是否将问题简化，且解出正确答案，取决于其在分类讨论的过程中能否做到合理、准确的推理与判断。因此，教师应引导学生分析基于各种条件下数学研究对象呈现出来的异同点，并进行精准划分，再分别求解，以得出正确的结论。

案例五：已知a∈R，函数f（x）=x2|x-a|，求函数y=f（x）在区间［1，2］上的最小值。

解析：通常在解题时可以先将函数f（x）化为分段函数，再运用导数对比函数在区间［1，2］上的单调性，以解出最小值。在此过程中能够明确无法与字母的取值分开，因此可以确定字母是引起分类讨论的因素。此时学生会对先整体还是先局部以及分类的标准产生疑问，对此，教师应引导学生对解题时的“分歧点”展开分析，也就是在函数f（x）图象上，区间［1，2］所处的位置。教师可以先让学生从整体出发，观察函数f（x）图象，发现无法确定函数f（x）的零点等于0 或x=a的大小，进而应对三种情况展开讨论：a＜0，a=0，a＞0。在求出函数f（x）的导数后，可以对区间［1，2］与的关系展开分析，当［1，2］时，应明确f（1）与f（2）的大小关系后才能求出最小值。此题需要分三层展开分类讨论，若想化解去绝对值和分段函数的问题，可以根据函数f（x）=x2|x-a|的结构特征与函数的定义域［1，2］对a和x的大小关系进行分析，然后再分别对a≤1，1＜a≤2，a＞2 进行讨论即可。