一题多解，多解同道——以2022年全国高中数学联赛四川预赛第6题为例

张 君 李武学

四川省温江中学

1 预赛试题

2022年全国高中数学联赛四川预赛第6题如下：

若△ABC的三边a，b，c满足a2+b2+3c2=7，则△ABC面积的最大值为.

这是只有一个条件的求三角形面积的最值问题，属于中档题.注意到已知等式中a，b，c均带平方，且a与b是对称的，所以在选择面积的表示方法时，要充分考虑到这些因素，为下一步求最大值做好铺垫.

2 解法探究

设△ABC面积为S.

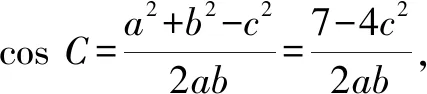
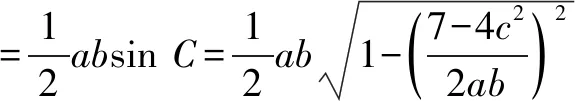
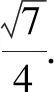
解法2：

解法3：设AB边上的高为h，则

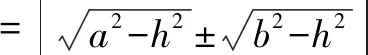
所以c2≤14-6c2-4h2,即7c2+4h2≤14.

解法4：设AB边的中点为D，则

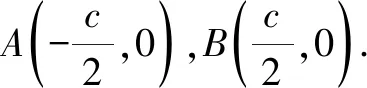
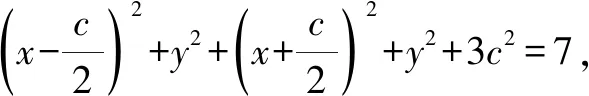
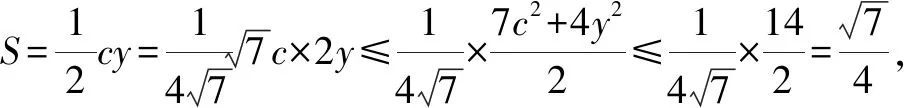
3 题后反思，探求多种解法中的一般规律

这五种解法都包含面积的表示方法和求最大值的方法两个主要方面.

(1)面积的表示方法.因为三角形的面积公式比较多，而且用同一个公式也有不同的切入点，这就导致了这类题的解法多样，这五种方法就是这样产生的.不同的表示方法也基本决定了后面解题过程的走向和难易程度，所以选一个好的面积表示方法很重要.

(2)求最大值的方法.这五种方法求最大值的过程看起来都不一样，但基本方法其实有共同之处：都对式子进行放缩，直到得出定值，只要掌握了选择放缩对象的方法，基本就等于掌握了解这类题的钥匙.因为成功的放缩必须保证等号能成立，而基本不等式一般有两大特点：式子具有对称性，等号成立的条件多数是变量相等.注意到条件a2+b2+3c2=7中a和b是对称的，所以，五种解法都把由a和b组成的对称式作为放缩的对象，这样能保证等号成立.

从以上分析可知，选择一种好的表示方法(在构造出对称式有对称变量的情况下)作为放缩对象就是解这类问题的钥匙.

4 变式推广，由会解一道题到会解一类题

因为四边形是由两个三角形构成的，因此，容易想到与本题条件相似的四边形面积的最值问题，也能用类似的方法解决.

原创题设平面凸四边形ABCD的四边长分别为AB=a,BC=b,CD=c,DA=d.

(1)若a+b+c+d=8，求四边形ABCD面积的最大值；

(2)若a2+b2+2c2+2d2=8，求四边形ABCD面积的最大值；

(3)若3a2+3b2+3c2+d2=6，求四边形ABCD面积的最大值.

解：设四边形ABCD的面积为S.

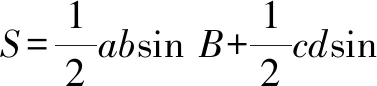
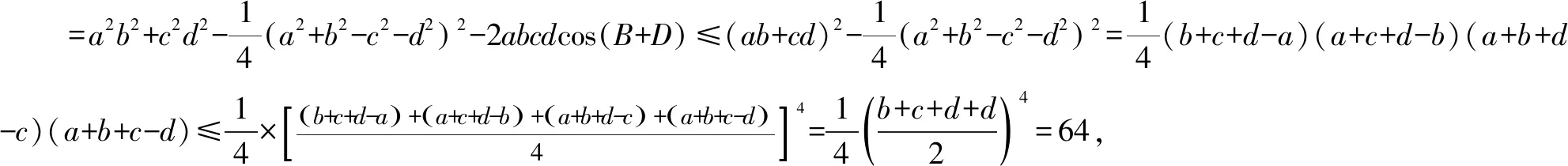
当且仅当∠B+∠D=π且a=b=c=d=2，即ABCD为正方形时,S=4.

所以四边形ABCD面积的最大值等于4.

(2)由(1)知

(3)由(1)知

16S2≤(b+c+d-a)(a+c+d-b)(a+b+d-c)·(a+b+c-d)

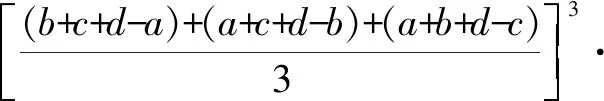
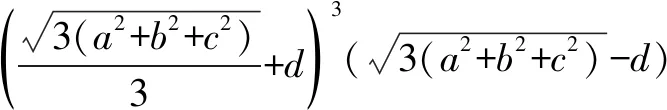
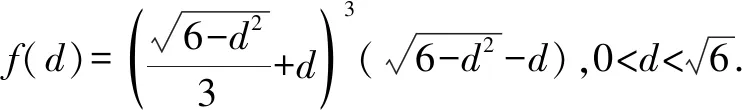
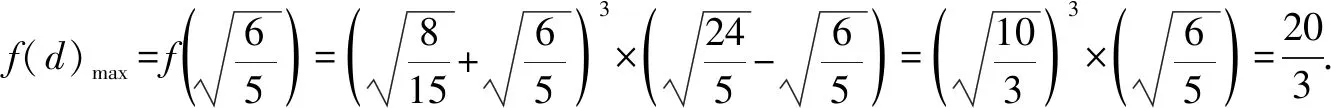
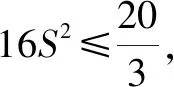
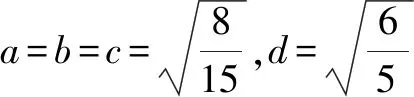
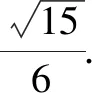
我们经常说要跳出题海，提高效率.怎么才能做到这一点呢？这种解题后进行反思归纳，提炼出解题的一般规律，进而掌握一类问题解法的做法，可以收到事半功倍的效果，对提高学习效率大有好处.Z