多思维策略，妙方法破解——对2021年数学新高考Ⅰ卷第6题的探究

崔德全

山东省菏泽市定陶区第一中学

三角函数式的化简与求值一直是历年高考数学试卷中的一个基本考点，或单独设置问题考查，或交汇融合其他知识辅助考查，或作为基本过程合理过渡，常考常新，变化多端，形式各样；而且由于三角函数中公式众多，切入点多维，破解方法多样，对逻辑推理与代数运算的能力与素养要求比较高，是考查考生综合能力和核心素养的良好载体.

1 真题呈现

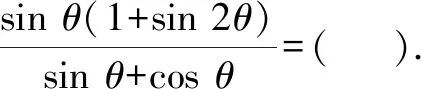
2 真题剖析

该题条件简单，短小精悍，难度适中，以三角函数中单角的正切值为条件，通过单角、倍角的三角函数式的求值来巧妙设置，综合考查三角恒等变换、同角三角函数基本关系式等相关基础知识.

正确进行三角函数求值的关键就是化同角，巧变换，妙求值.具体破解时，可以通过三角关系式的齐次化策略、统一化策略、各个击破策略以及定义化策略等思维方式来处理，结合不同的思维方法来处理与求值，很好地考查学生对三角函数综合知识的理解与掌握程度，进一步强化思维的灵活性、多样性、拓展性等.

3 真题破解

方法1：齐次化策略

解析：由tanθ=-2，得

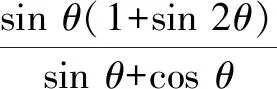
故选择答案：C.

点评：由题意利用二倍角公式化简所给的三角函数式，然后利用齐次式的特征进行除“1”的齐次化处理，利用分式的分子分母同除相应的余弦二次式，转化为含有正切的关系式，代入即可求得三角函数式的值.齐次化处理，两次化“1”处理，以及同除变形，是破解此类问题最常用的技巧方法.

方法2：统一化策略.

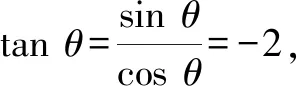
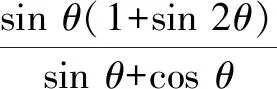
故选择答案：C.

点评：利用题目条件中的正切值转化为正弦与余弦之间的关系，代入平方关系得到余弦的平方值，结合所求的三角关系式统一转化为余弦表达式，代入余弦的平方值即可求得三角函数式的值.借助条件与平方关系确定余弦的平方值，统一转化，化同名变形，巧妙代换处理，简捷有效.

方法3：分类讨论策略.

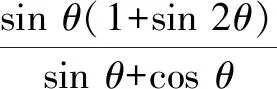
=sinθ(sinθ+cosθ).

①

由tanθ=-2<0，可得θ的终边在第二象限或第四象限.

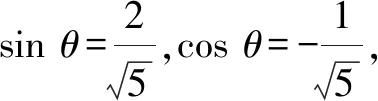
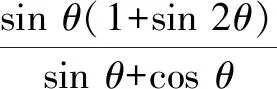
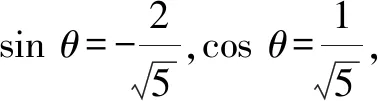
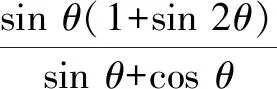
点评：利用题目条件中的正切值为负，确定角θ所在的象限，通过分类讨论，分别确定对应角在相应象限内的正弦值与余弦值;代入分别求值，进而求得三角函数式的值.根据题目条件确定对应角的三角函数值，是破解三角函数求值中问题最常见的思维方式，必须借助角的不同象限进行分类讨论.

方法4：整体化策略.

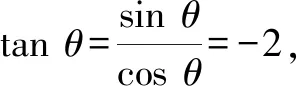
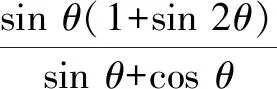
故选择答案：C.

点评：不分别计算正弦与余弦值，而是把正弦的平方以及正弦与余弦的乘积分别作为一个整体求值.整体化求值避免了分类讨论，更加有效快捷.

方法5：定义化策略.

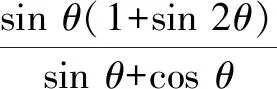
故选择答案：C.

点评：结合三角函数的定义，利用题目条件中的正切值转化为参数y与x的关系式，进而确定正弦值及余弦值与r的关系式；由题意利用二倍角公式化简所给的三角函数式，结合三角函数定义代入，并对参数进行变形与化简，即可求得三角函数式的值.定义化破解三角函数问题，回归问题本质，也是破解三角函数求值问题中比较常见的一类技巧策略.

4 变式拓展

探究角度：改变问题的给出方式，变原来“tanθ=-2”为“角θ的终边落在直线y=-2x上”，间接处理，可以进一步融合相关数学知识，强化数学知识的理解与掌握以及数学能力的提升.

5 教学启示

(1)在掌握常规破解方法的基础上适度拓展

涉及三角函数式的化简或求值问题，相关公式众多，关系错综复杂，有利有弊.有利的一面是可以多角度多层面选择三角函数的相应公式加以应用；有弊的一面是容易陷入三角函数的相应公式无从选择的困境.因此，在这部分的教学与学习过程中，除了要熟练掌握破解此类问题的常规方法外，还要有针对性地适度拓展对其他一些思维方法的理解与掌握，以防不时之需.

(2)回归课本，挖掘潜能

充分回归课本，挖掘课本的基本知识，有效拉近课本与高考之间的距离，架起两者之间的桥梁，是平时数学与学习的一个关键所在.特别要有意识地针对一些典型高考真题，就某一层面的知识体系加以“一题多解”“一题多变”“多题一解”等方面的剖析，结合课本基本知识与基本方法，从多个视角切入，到多个思维方法破解，真正达到“横看成岭侧成峰，远近高低各不同”的境界.Z