多方法破解，多规律总结，多变式拓展——对2021年数学新高考Ⅰ卷第5题的探究

邓 杰

江苏省海门中学

1 真题呈现

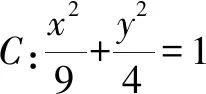
A.13 B.12 C.9 D.6

该题题目简洁明了，通过椭圆标准方程的给出，进而确定椭圆两焦半径积的最大值.题目难度不大，破解思维方式多样.破解最直接有效的办法就是应用基本不等式；而采用两点间距离公式或焦半径公式也是不错的方法，结合函数思维来确定最值；针对选择题的特点，可直接利用极端思维来确定两焦半径积的两个极端取值，进而得以合理判断.不同的破解方法，展示不同的思维方式.

2 真题破解

方法1：基本不等式法.

解析：由于F1，F2是椭圆C的两个焦点，则a=3，而点M在C上，利用椭圆的定义可得|MF1|+|MF2|=2a=6.

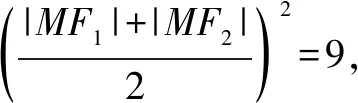
故选择答案：C.

点评：根据椭圆的标准方程确定相应参数的值，利用椭圆的定义得到两线段的长度之和，结合基本不等式即可确定两线段长度积的最大值.结合椭圆的定义，借助基本不等式来确定关系式的最值，是破解此类问题中最常见的一种基本方法，思维直接，简单快捷.

方法2：距离公式法.

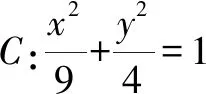
又|MF1|·|MF2|

当且仅当x=0时等号成立.

故选择答案：C.

点评：根据椭圆的标准方程确定相应参数的值，设出动点M的坐标，利用两点间的距离公式确定两线段长度积的关系式，通过消参、等价变换，得到相应的二次函数，利用二次函数的图象与性质来确定对应的最大值即可.通过距离公式来转化线段的长度问题进而转化为函数问题，利用函数的图象与性质来确定最值,是破解此类平面解析几何相关问题的常用方法.

方法3：焦半径公式法.

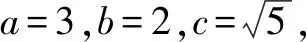
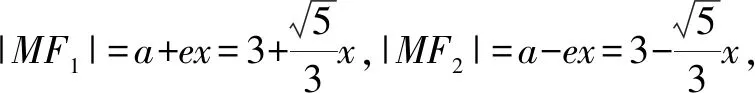
故选:C.

点评：根据椭圆的标准方程确定相应参数的值，并求得椭圆的离心率，设出动点M的坐标，结合椭圆的焦半径公式分别确定|MF1|与|MF2|的表达式，进而确定两线段长度的积关系式，得到相应的二次函数，利用二次函数的图象与性质来确定对应的最大值即可.焦半径公式是圆锥曲线中的拓展与提升，是破解与焦半径有关问题的基本方法.

方法4：极端思维法.

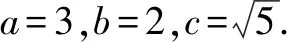
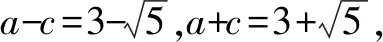
当动点M与短轴的顶点重合时，|MF1|,|MF2|的值均为a=3，此时|MF1|·|MF2|=9.

所以|MF1|·|MF2|的最大值为9.故选C.

点评：根据椭圆的标准方程确定相应参数的值，结合椭圆图形的对称性，借助极端思维，利用动点M与椭圆长轴的顶点、短轴的顶点重合时，对应的线段长度以及两线段长度的积，通过比较来判断相应的最大值问题.极端思维在解决平面解析几何中的相关问题时，以极端的特殊思维来解决，极具可行性.

3 规律总结

根据以上高考真题及其对应的破解过程，特别是方法2～4，除了确定相应的最大值外，还可以确定相应的最小值问题.参照以上破解方法，总结规律，可以得到以下几个相应的一般性结论.

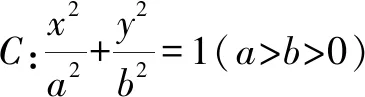
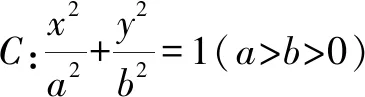
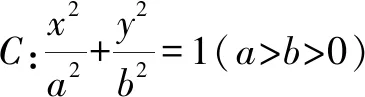
结论的证明，可以直接参照以上高考真题的破解方法2～4中的过程，具体加以实际分析即可，这里不多加赘述.

4 变式拓展

保留题目条件，改变所要求解的关系式，变原来“两焦半径的积”为“两焦半径的平方和”，可以得到以下两个对应的变式.

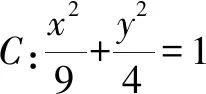
A.28 B.24 C.18 D.12

解析：由于F1，F2是椭圆C的两个焦点，则a=3.而点M在C上，利用椭圆的定义可得|MF1|+|MF2|=2a=6.

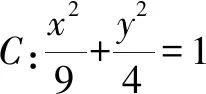
A.28 B.24 C.18 D.12

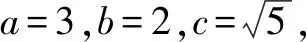
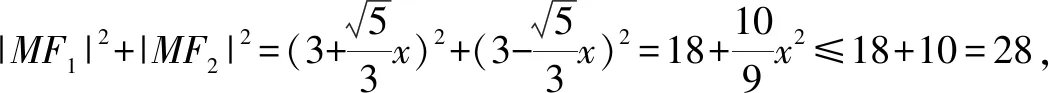
当然，融合变式1与变式2的结论，又可以进一步得到确定椭圆的两焦半径的平方和的取值范围问题，这里就不另展示.

5 教学启示

(1)研究高考典型真题不能只以难题为标准

历年高考过后，都会有很多的教师去研究一些高考典型真题，基本上选择一些选择题、填空题或解答题的压轴题之类的难题来研究，这样固然可以挖掘问题本质，突破问题的难点.但对大部分学生而言，基本题与基本方法才是根本，因而一些简单题也是研究的一大方向，不能掉以轻心.

(2)研究一题必有所得

深入研究一些基本的高考典型真题，从问题的类型、出题的落脚点、问题的知识点、切入的突破点等方面，都可以得到很好的体会，进而不断发展解题思维，展示解题方法，总结解题规律，探究变式拓展，引领并指导学生跳出题海，提升数学品质，提高数学能力，培养数学核心素养.Z