2021年高考数学全国乙卷(理)第4题的探究

朵天举

甘肃省民乐县第一中学

抽象函数是以中学阶段所学的基本初等函数为背景抽象而得到的一类更具一般性的函数，此类函数简单、抽象，更加灵活多变，是历年高考中的一类常见考点，倍受关注.破解此类涉及抽象函数的数学问题，从研究抽象函数的背景入手，通过直接代入、类比，猜想出它们可能为某种类型的基本初等函数，通常可找到解题的切入点，进而加以解决.

1 真题呈现

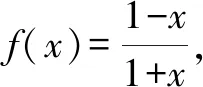
A.f(x-1)-1 B.f(x-1)+1

C.f(x+1)-1 D.f(x+1)+1

2 真题分析

该题以一次分式函数为问题背景，结合函数图象的平移变换来确定抽象函数的奇偶性.题目条件明了，难度中等及偏下.直接利用函数图象的性质、奇函数的定义、函数图象的平移变换规律等来破解，简单易懂；也可以利用特殊点来加以巧妙验证，或利用函数性质来处理，都可以达到解题目的.

在实际破解过程中，在一个43人的高一新生班中，已经学习过函数知识(高一下学期)，结果五分钟内做错该题的人数达到一半以上.当然，由于学校层次、学生层次不一样，可能这不代表所有学生的实际情况，但还是能说明此题看似简单，学生在实际解答时还是有一定的困难，有必要对其加以认真剖析，归纳解答方法，总结解题规律，探究拓展提升.

3 真题破解

方法1：平移变换法.

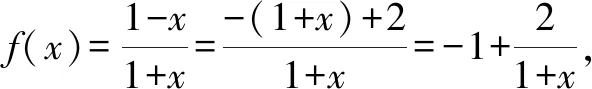
点评：先根据对函数f(x)解析式的变形处理，得到f(x)的对称中心，然后通过函数图象的平移变换，使得变换后的函数图象的对称中心为(0，0)，从而得到答案.平移变换法处理此类图象变换问题时，要注意平移的方向与符号的关系，关键是注意对称中心或对称轴的确定.

方法2：逐一代入分析法.

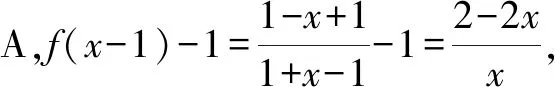
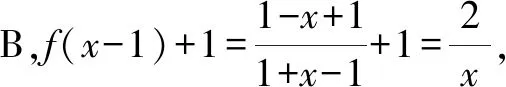
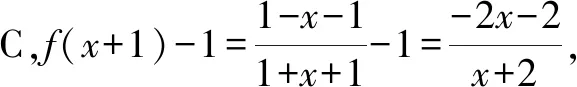
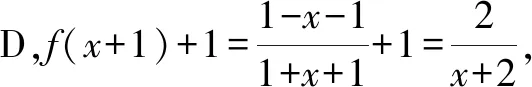
综上分析，故选择答案：B.

点评：根据题目条件中的函数解析式，通过各选项中的抽象函数关系式进行逐一代入处理，结合代入后所确定的函数解析式来判断相应函数的奇偶性.逐一代入分析法，方法直接“粗暴”，分析与处理过程相比较更为复杂一点，但更直观、更具体，判断起来更加简单快捷.

方法3：奇函数定义法.

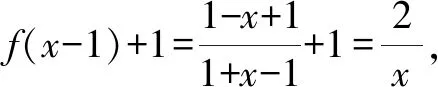
点评：抓住奇函数的定义，函数定义域关于坐标原点对称时，满足f(-x)=-f(x)即可判断其是奇函数.根据各选项中的抽象函数解析式，通过代入函数解析式进行合理验证，结合相应的定义加以正确判断.奇函数定义法是抓住定义本质，通过建立相应的函数关系式来合理运算，巧妙判断.

方法4：特殊值验证法.

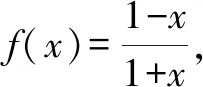
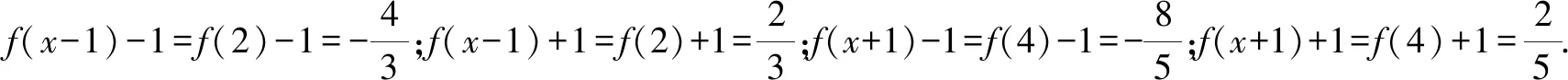
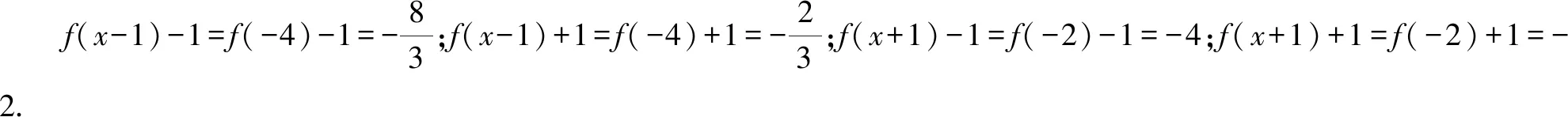
对比相应的函数值，则函数图象关于坐标原点(0，0)成中心对称的只有函数f(x-1)+1，即函数y=f(x-1)+1为奇函数.故选：B.

点评：根据特殊点，分别取互为相反数的自变量(这里取3与-3，不能取使得分母没有意义的自变量)，若所对应的函数值互为相反数，则对应的函数的图象就是关于坐标原点(0，0)成中心对称.通过特殊点的选取与函数值的运算来验证，虽然过程比较繁杂，但也是一种不错的破解方法，特别是在没有任何思路的情况下.

方法5：函数性质法.

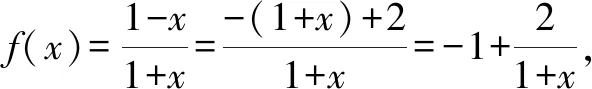
点评：根据题目条件，通过确定函数图象的中心对称点，根据函数的基本性质来直接应用加以解决问题函数图象的平移变形处理.掌握函数的基本性质是破解此类问题的关键，而此类结论在教材中没有具体要求，作为课外拓展与提升的知识，为进一步的探究与变式提供条件.

4 变式拓展

探究：根据以上高考真题及其对应的破解过程，进一步将函数加以提升与抽象，化具体的函数为抽象函数，给出抽象函数的中心对称点，进而判断对应抽象函数的奇偶性，从而得到更具一般性的变式问题.

变式设函数f(x)的图象关于点(-1，-1)成中心对称，则下列函数中为奇函数的是( ).

A.f(x-1)-1 B.f(x-1)+1

C.f(x+1)-1 D.f(x+1)+1

解析：根据以上问题的破解过程，当函数f(x)的图象关于点(-1，-1)成中心对称，则有函数y-1=f(x-1)的图象关于坐标原点(0，0)成中心对称，即y=f(x-1)+1为奇函数.故选：B.

结论：若函数y=f(x)的图象关于点(m，n)(m，n∈R)成中心对称，可知函数y+n=f(x+m)的图象关于坐标原点成中心对称，即函数y=f(x+m)-n为奇函数.

5 教学启示

(1)熟悉掌握函数图象平移变换的方向与符号之间的关系

在具体的函数图象的平移变换过程中，掌握“左+右-”的基本规律，即函数的图象向左(或向右)平移1个单位，利用“x+1”(或“x-1”)来代替原来函数解析式中的“x”即可达到目的.

(2)注意函数图象平移变换时的相对运动

在实际解决问题中，要注意函数图象平移变换的运动规律，确定运动前后所对应的函数解析式，特别注意在一些问题中的正向思维与逆向思维的应用.

(3)掌握具有奇偶性、周期性函数图象的基本特征

奇函数的图象关于坐标原点(0，0)成中心对称；偶函数的图象关于y轴成轴对称；周期函数的图象关于最小正周期重复出现.在实际破解问题时，要注意抓住此类特殊性质函数图象的基本特征与对应定义之间的关系，合理构建函数图象的变化特征与对应关系式之间的联系.Z