开展深度学习 提高学习效率

张隆传

浙江省宁波市姜山中学

在素质教育的影响下，高中数学课堂的教学模式、教学手段、教学评价都发生了重大变革，并取得较好效果.但还存在一些问题，“题海战术”依然是高三数学复习的主旋律.不可否认，“题海战术”也能让学生获得一些收益，在一定程度上可以提升解题速度和解题信心，但题海无边，如果不进行反思和总结，每天只是埋头苦干，不仅学得苦，而且收获甚微.对于教师亦是如此，课上讲，课下批，将大多数的时间和精力都用于评讲上，占用了对学生进行个体化分析的时间，为此“因材施教”的教学方针将难以有效实施.可见，这是一种“高耗能”的学习模式，不利于高三复习效率的提高.

那么如何变“高耗能”为“高收益”呢？笔者认为在高中数学教学中，尤其在高三复习阶段，要引导学生进行深度学习.所谓深度学习就是打破“就题论题”式的表面化学习状态，深入问题的本质进行分析，从本质和思想上深层建构，使学生在解决一个问题的基础上可以理解并掌握解决一类题的思想和方法，进而提升学习效率.为了开展深度学习，教师要从学生的认知出发，精挑细选一些具有代表性和挑战性的学习主题，让学生积极参与，并全身心地投入到整个学习过程中.在此过程中通过思考、交流、合作等有意义的学习活动，掌握核心知识，提炼出重要的思想方法，从而在获得成功体验的同时，归纳总结出有价值的东西来，以此激发学生的内在学习动机，使学习更具方向性和目的性，让学生在提升“四基”的基础上，形成积极的态度和正确的价值观，进而在提升学习效率的基础上，培养学生的合作意识和创新精神，让学习变得既高效又有意义.

那么在高三复习阶段应该如何开展深度学习呢？笔者结合教学经验，下面谈几点培养深度学习的策略，仅供参考！

1 重基础，通概念

数学概念是数学学习的核心，是对数学对象本质属性的直接表述，是开展深度学习的基础.在开展深度学习时必须重视对概念、定理等基础知识的梳理，这是达成理解的必要条件.但是在高三复习阶段，部分教师常忽视基础知识的再学习和再梳理，将教学的重心放在难题和新题上，片面认为学生只要难题会了，简单的问题自然就通了.然而学生没有扎实的基础，导致难以理解题目的本质，在解题时常生搬硬套，不仅没有提升解题能力，而且影响了解题信心，得不偿失.同时，也有部分教师为了完成教学任务，追求课堂容量，教师主导课堂，学生的主体作用难以发挥，为了追赶教师的节奏，学生忙于解题，对基础知识的再学习时间很少，为此也不利于“四基”的巩固，不利于学生认知体系的完善.要知道，一道真正有意义的题目并不是因为它有多难、多新，而是通过这道题可以让学生认清问题的本质，掌握解决问题的通法；同时，通过挖掘问题的各个方面引导学生建构完善的认知体系，从而通过一道题辐射到一类题，进而达到会一题通一类的效果.这样可以帮助学生脱离“题海”，避免重复性练习所带来的思维定式和思维疲劳，让学生有时间和精力投入到更有意义的学习中去.

例1已知定义在R上的奇函数y=f(x)满足f(2+x)=f(2-x)，当-2≤x<0时，f(x)=2x，则f(2 013)=.

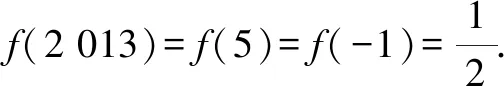
题目讲解后，教师发现很多学生仍然露出疑惑的表情，为此决定“小题大做”，对问题进行深入剖析.

师：这是一道典型的考查函数对称性和周期性的问题，现在一起复习一下与之相关的概念.(在教师的带领下，学生复习了轴对称和中心对称的相关概念，又结合图象重温了函数周期性的相关应用.)

师：对于以上求解过程，你们认为哪一步是难点呢？

生1：函数的周期.

师：对于例1，你是如何判断它的周期的呢？

生2：我是用图象法.(教师让学生在黑板上展示了画图过程.)

生3：图象法是很直观，但是画图需要的时间较长，可以直接应用函数的性质进行判定.

师：说说你的想法.

生3：因为y=f(x)为奇函数，所以f(2+x)=f(2-x)=-f(x-2)，由此可得f(x+4)=-f(x)，所以f(x+8)=-f(x+4)=-[-f(x)]=f(x)，由此可知f(x)的周期为8.

师：很好！借助“数”和“形”两种方法得到了函数的周期，解决了这一难点后，问题也就迎刃而解了.

虽然带领学生回顾基础知识占用了较长的时间，但是通过细致的分析和回顾，学生不仅将本题学懂吃透了，而且对函数周期等问题又有了更深层的理解，其影响是深远的.本题虽然难度不大，但若学生对相关基础知识掌握不牢，要想顺利求解也是较为困难的.所以在高三复习阶段不能好高骛远，要放低起点，通过缓坡让学生思维螺旋上升，这样既有助于夯实基础，又能让每个学生都有所收获，让他们的理解能力梯度上升.

2 重训练，讲方法

学习数学自然离不开解题，尤其学生运算能力的提升更是与平时的训练息息相关.高考非常重视对学生运算能力的考查，运算能力的强弱很大程度上将直接影响高考的分数.那么运算能力应该如何提升呢？其实，运算能力并不是简单的计算，其中还涉及观察能力，总结归纳等综合能力.为此，培养学生的运算能力时要重视基础知识的积累，只有准确理解才不会因为理解偏差而出现错解；同时要善于优化解题方法，进而有效避免复杂的运算过程，降低错解的风险；另外要重视数学思想方法的科学指导，根据已知寻求更加快捷有效的解题途径，以此来提升运算效率，提高解题准确率.

图1

本题是一个综合性较强的典型的动点问题，解题方案并不唯一.解题方案不同，其运算过程势必也会不同.教师带领学生从不同角度进行观察和分析，寻找不同的解决方案，通过对运算过程及运算繁简进行深度剖析，最终找到了最优解题方法.

在数学教学中不要急于求成，对于一些典型性问题要重点分析，引导学生通过多角度观察和多维度探究来丰富解题经验，同时将不同解题方案进行对比，寻求解决问题的通法和最优解决方案，以此来提升学生解决此类问题的运算能力.

3 重过程，促发展

在日常教学中为了追求效率，常出现“重结论、轻过程”的现象，忽视了对学生思维能力和自主学习能力的培养，使学生的解题思路过于保守和单一.其实，无论在新知授课，还是在例习题的讲解中都要重视过程的分析，要充分暴露学生的思维过程，进而对暴露的问题进行引导和矫正，带领学生走出思维的误区.同时，只有经历过程才能发现思维的“闪光点”，进而在鼓励和引导下，培养学生的独创力.

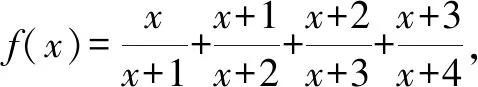
本题虽然有一定难度，但并不是完全不能求解.为此，教学过程中教师坚持“以生为主”，通过合作交流展示学生的思维过程，从而在过程中发现不足，在交流中共同提升.

师：很好，踏实的计算也是优秀的品质，平淡却不平凡.你们还有其他的解决办法吗？

生2：已知条件中的函数表达式是有一定特点的，所求的值也是有规律的，求解时不应该急于代入，应该先找到内在联系，挖掘内在规律，只是还没有发现.

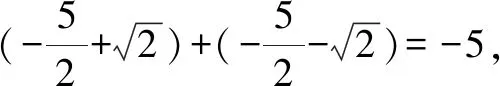
通过过程分析不仅准确地求得了答案，而且通过对特殊的挖掘揭示了问题的真面目，让学生充分享受数学分析推理的乐趣，学生的分析能力.推理能力、运算能力也得到较大提升.

总之，若要提高高三复习效率，教师在教学中就需要对教学内容进行“深加工”，引导学生回归问题的本质，通过对重要思想方法的提炼和总结，促进解题能力、思维能力全面提升.Z