回归函数本质，提升数学能力

陶虹萍

广西防城港市高级中学

函数是高中数学的重要基础知识，贯穿于整个高中数学体系，是历年高考数学的一个重要考点.在高考数学试卷中，涉及函数的知识往往以“2+1”(两个小题，一个大题)的形式考查，一般占分为20分及以上，“函(数)”概重点知识，“导(数)”向高考的命题趋势与考查热点.破解涉及函数的高考试题，一定要正确回归函数本质，让学生学会从最基本的函数概念出发去理解数学问题，根据函数性质与数学运算去推理、演算、论证，结合数学思维去思考与分析问题，借助相应的技巧方法去解决函数问题，利用相关的数学知识来综合与应用.

1 关注函数概念，回归数学本源

函数概念是函数的本质属性，涉及函数概念的问题也是高考中比较常见的一类题型，其破解的实质就是回归数学本源，通过相关函数概念建立联系，构建方程、不等式等来合理解决.

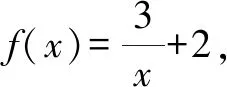
分析：结合题目条件，要求解反函数中的函数值问题，利用反函数的概念，即求解原函数中对应的函数值即可.

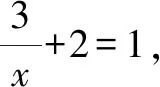
故填答案：-3.

点评：在破解一些函数的相关问题中，经常要合理关注函数的基本概念，切实回归数学基础，从根源上切入数学问题的实质，回归数学本源，合理建立相应的联立，构建对应的方程、关系式等，进而得以合理解决.

2 关注函数求值，回归数学基础

函数求值问题往往以形式多样的题型在高考试卷中出现，或分段函数，或实际应用，或融合交汇.剖析函数问题的本质，结合函数求值，回归数学基础，合理构建联系，巧妙破解涉及函数求值的数学问题.

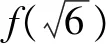
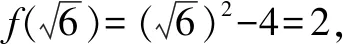
故填答案：2.

点评：对于分段函数的求值与应用问题，解题的关键就是回归数学基础，根据自变量的值所对应的解析式加以“对号入座”或分类讨论，建立相应的联系以及对应的关系式，合理构建，巧妙转化.

3 关注函数性质，回归数学内涵

函数性质是历年高考数学试卷中最常见、最基本的考点，通过函数的单调性、奇偶性、周期性等基本性质，或显性表现，或隐性包含，充分挖掘与应用函数的基本性质，回归数学内涵，巧妙破解数学问题.

例3(2021年高考数学新高考Ⅰ卷第13题)已知函数f(x)=x3(a·2x-2-x)是偶函数，则a=______.

分析：通过函数基本性质的应用，借助函数奇偶性的相互转化，把偶函数转化为奇函数，利用奇函数的性质代入应用，进而确定对应的参数值.

解析：由于函数f(x)=x3(a·2x-2-x)是偶函数，而y=x3为R上的奇函数，利用函数的基本性质，可知y=a·2x-2-x也为R上的奇函数.

借助奇函数的性质，可得a·20-20=a-1=0，解得a=1.

故填答案：1.

点评：熟练利用函数的基本性质，巧妙将条件中涉及函数解析式的问题进行拆分或组合，合理转化并应用函数的基本性质，从而达到巧妙解决函数问题的目的.

4 关注数学运算，回归数学规则

数学运算是函数问题中最基本的数学规则，借助幂指数运算、对数运算等运算法则与应用，合理“串联”起函数的相关基本知识，或直接利用函数应用，或交汇融合其他知识，得以合理应用，巧妙破解.

A.-1 B.lg 7

C.1 D.log710

分析：通过剖析题目条件，将给出的指数式进行对数化处理，然后合理分离参数，巧妙代入所求的代数式，结合对数运算与合理变形来进行有效地化简与求解.

解析：由条件2a=5b=10，两边同时取常用对数，可得alg 2=lg 10=1，blg 5=lg 10=1.

故选择答案：C.

点评：在函数问题中，幂指数、对数等基本运算是最常见的一些基本数学运算，破解此类运算问题，巧妙同底化处理，指(数)对(数)互化，幂运算与对数运算法则等都是必须熟练掌握的基本数学规则.

5 关注技巧方法，回归数学应用

技巧方法是破解函数问题比较特殊的一类策略，借助一些函数问题中的基本技巧方法，可以更加简单快捷地处理涉及函数的相关问题.比如,利用特殊值确定函数的大致图象，借助特殊函数的构建来确定函数的基本性质，等等.

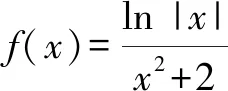
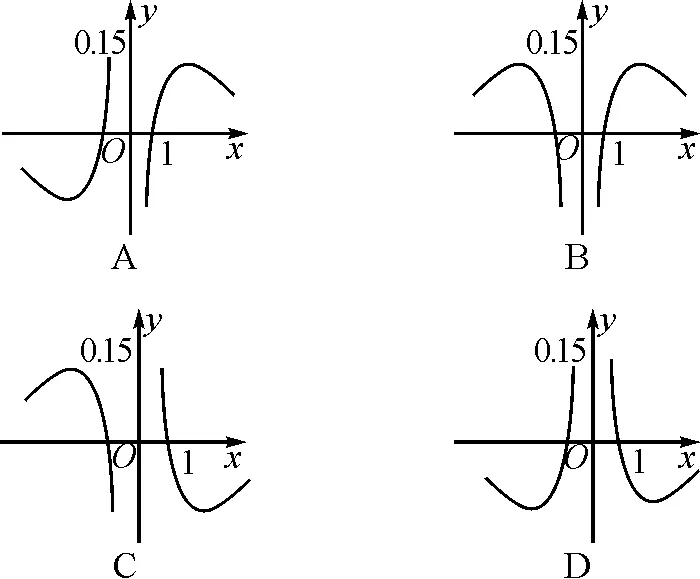
图1

分析：结合条件中给出的函数解析式，先通过确定其定义域，结合奇偶性的定义判断函数图象的对称性，再结合自变量的取值情况加以分类讨论确定其函数值的正负情况，从而得以确定函数图象的大致情况.

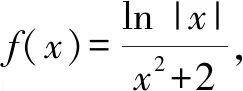
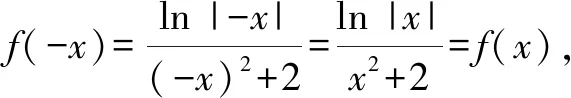
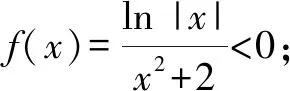
故选择答案：B.

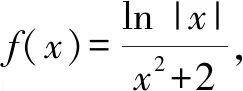
故选择答案：B.

点评：借助常规方法，结合函数解析式，从定义域、函数性质、函数值等角度切入，对比分析，合理排除，正确破解.而借助特殊值代入，通过特殊值所对应的函数值的正负情况，直接加以排除，从而得以巧妙判断，更快更简捷.

回归函数本质，从函数概念、函数性质、数学运算、技巧方法等思维视角切入，有效培养、形成、发展和拓展解题思维与方法，形成正确分析问题与解决问题的能力，从而简捷快速解题，提高解题效率，提升数学能力，培养数学核心素养.Z