活用数学教材 挖掘习题特质——以一道课本习题探究一类指数型分式函数的对称中心

唐新阳

湖南省宁乡市第一高级中学

1 问题的提出

人教版各版教材的复习参考题中都有一道以下习题：

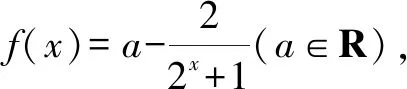
该习题在2019版的人教版教科书必修第一册第161页依然编入，可以看出历任编者对该道习题的情有独钟.结合新教材第87页关于函数对称中心问题的研究，本文中以该习题为例探究一类指数型分式函数的对称中心.

2 问题的初探

关于奇偶性的讨论，注意到函数定义域为R，可以有较多方式探究.此处仅以奇偶性定义求解.

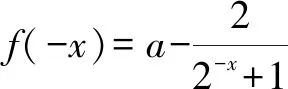
3 问题的引申与探究

3.1 直接求解

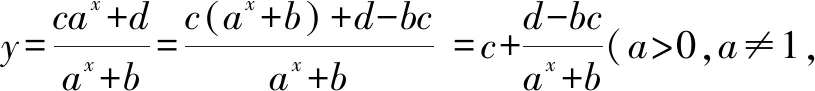
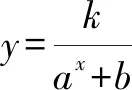
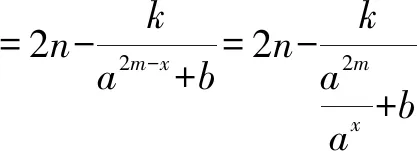
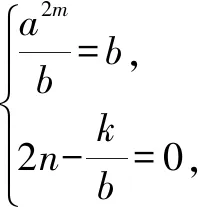
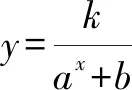
3.2 利用奇偶性的引申结论

人教版教材必修一第87页有如下结论：函数y=f(x)的图象关于坐标原点成中心对称图形的充要条件是函数y=f(x)为奇函数，可以将其推广为:函数y=f(x)的图象关于点P(a,b)成中心对称图形的充要条件是函数y=f(x+a)-b为奇函数.

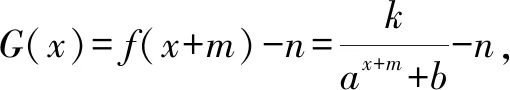
G(-x)=f(-x+m)-n

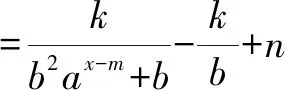
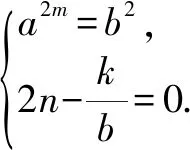
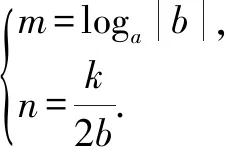
反之亦成立.

3.3 指数型分式函数的图象特点

(1)b>0

若b>0，则函数y=f(x)的定义域为R，且ax+b>b.

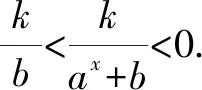
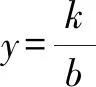
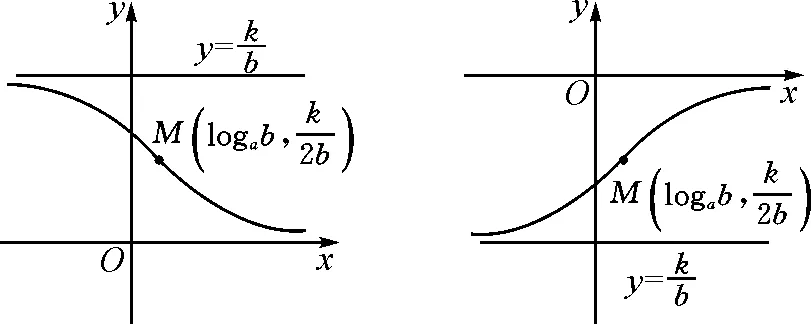
图1

(2)b<0

若b<0，则函数y=f(x)的定义域为{x|x≠loga|b|}，且ax+b≠0.

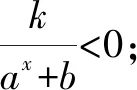
如图2，f(x)的图象类似于反比例函数的图象.

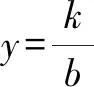
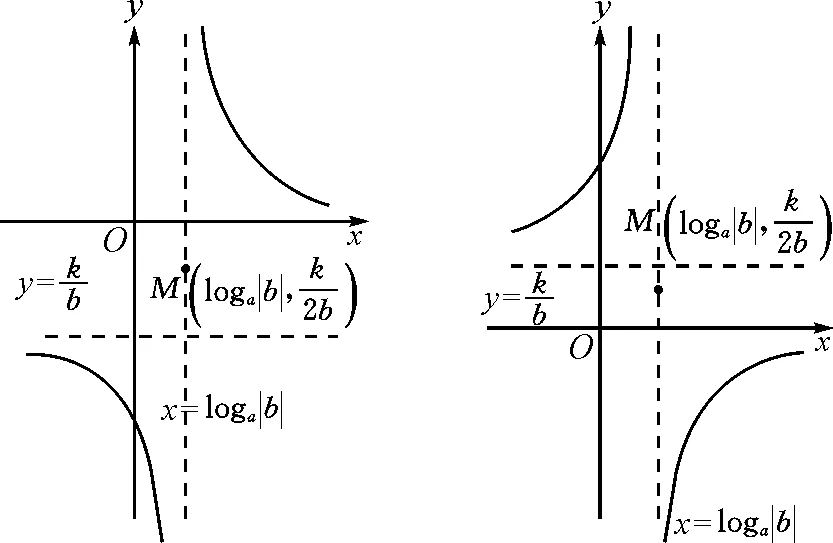
图2

(3)函数值之间的关系

4 问题的应用

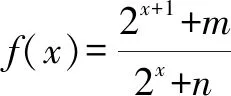
解析：f(x)是奇函数，则图象关于原点中心对称.如前所述，log2n=0，得n=1.又f(0)=0，则m=-2.

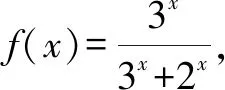
A.(-∞,1) B. (1,+∞)

C.(-∞,1)∪(1,+∞) D.(0，1)

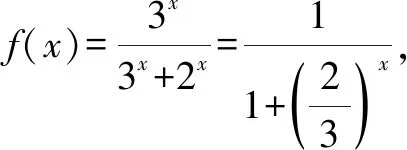
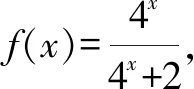
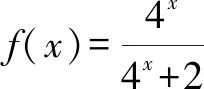
倒序得

两式相加，得2S=2 020.故S=1 010.

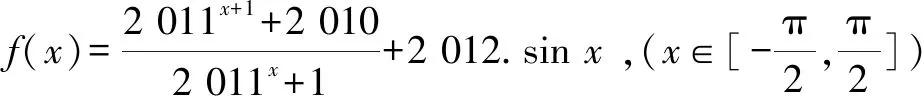
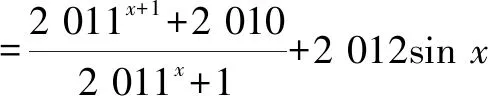
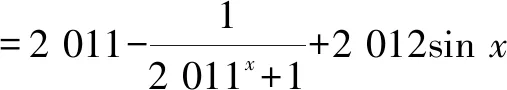
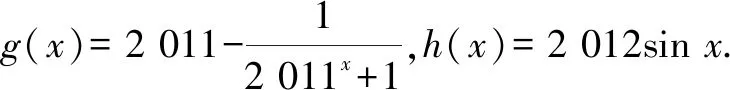
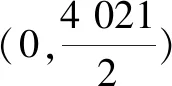
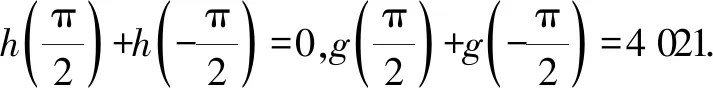
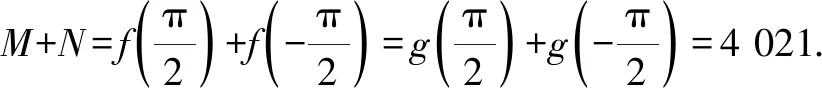
总之，以上内容最大限度地挖掘了教材中函数奇偶性在研究函数图象对称性上的应用，并对指数型分式函数模型的图象特点作了深入全面的研究，挖掘了教材内涵.Z