创新解题方法 培养创新能力
——以一道比较大小的选择压轴题为例
2023-02-11操厚亮
操厚亮
湖北随州二中
《普通高中数学课程标准(2017年版)》提出“四能”,即发现问题、提出问题、分析问题、解决问题的能力的总目标.数学中的创新往往始于问题,发现问题是创新的基础.数学家们常说:发现问题往往比结论更重要.因此,教师应适时、适度引导学生发现、提出一些数学问题,进而分析和解决问题,培养学生的数学学科核心素养和创新能力.
1 试题呈现
A.a C.a 观察四个数,不难发现0.1这个数高频出现,可以尝试构造函数,自变量x在包含0.1的一个区间内,如果这些函数在该区间内大小关系确定,那么在x=0.1处的函数值大小关系也确定.这体现了数学中的一种共性与个性的关系,一般与特殊的数学思想方法. 解法一:构造函数+放缩法. 故d(0.1)-b(0.1)>d(0)-b(0)=0,即d>b. f′(x)=ex(cos2x-sin 2x) =ex(-sin2x-sin 2x+1). 设g(x)=x-sinx,则g′(x)=1-cosx≥0,从而g(x)=x-sinx为增函数. 所以x∈[0,0.1]时,g(x)≥g(0)=0,即x≥sinx. 故f′(x)≥ex(-x2-2x+1)=ex[-(x+1)2+2],当x∈[0,0.1]时f′(x)>0,f(x)=excos2x-1为增函数,有f(x)≥excos20-1=0,从而当x∈[0,0.1]时,y=b(x)-c(x)为增函数. 故b(0.1)-c(0.1)>b(0)-c(0)=0,即b>c. 综上,d>b>c>a. 由解法一不难发现,上述构造的这些函数是常见的函数,借助图象,观察图象的上下关系进而比较数值间的大小关系,优化解法一则得下面的解法二. 解法二:图象+构造函数+放缩法. 图1 设f(x)=sinx-(ex-1)cosx,则 f(0)=0,f′(x)=(ex-1)(sinx-cosx). 于是tanx 故a 由解法二不难发现,这些构造的函数图象比较相似,接近幂函数在区间(0,1)上的图象,由此联想泰勒展公式的功能,可以借助泰勒展开式来估算. 推荐理由:本书辑录了著名经济学家厉以宁从中国改革开放至今的40篇代表性论文,篇目由厉以宁先生亲自审定。内容主要涉及中国经济体制改革,中国在经济发展过程中的探索与创新,中国经济的机遇与挑战,中国的农业、工业改革,以及与经济发展密切相关的教育、管理等方面的见解。这些文章都是厉以宁对中国经济发展时期的精辟论断,是他对中国经济自改革开放以来40年的不间断思考与研究精华,对中国今后的经济改革与发展具有重要的启示意义。 评:本题还可以用[2,2]阶帕德逼近来比较大小,但帕德逼近相对泰勒展开式来讲是一种精度更高的分式函数逼近,此处略去.有兴趣的读者可自行研究. 继续观察构造的这些函数的图象,不难发现,这些函数在0处的函数值均相同,不同的是其增长速度快慢有别.那么通过增长速度的快慢比较大小是一种创新的解法,到此完美突破难点. 解法四:研究函数在x=0处的增长速度,通过增长速度快慢比大小. 设g(x)=ex-1,则b=g(0.1). 设h(x)=tanx,则c=h(0.1). 又f(0)=g(0)=h(0)=k(0), 所以d最大. 又f″(0)≤h″(0)≤g″(0),所以a 综上可知,d>b>c>a. A.a C.c A.a C.c C.x>yD.2ex>y 答案:(1)C; (2)B; (3)D. 众所周知,比较大小的试题每年高考都有出现,尤其是近两年,精度越来越高,难度越来越大,方法越来越灵活多样.作差、作商、插值,以及简单的构造函数利用单调性比较已经不能解决变化着的新问题.如何快速突破此类问题刻不容缓,必备基本功除了不等式的性质、基本不等式,还需要熟悉常见的不等式,如,糖水不等式、对数糖水不等式、泰勒展开式(函数不等式:切线放缩、曲线放缩等),了解帕德逼近等知识.对本道题而言,容易想到的方法是构造函数作差求最值比较大小,体现了一般到特殊的思想方法,对用导数的方法研究最值和计算求解能力要求较高,而用泰勒展开式和帕德逼近来估算的话,思维降维了,但站位较高,这些都是高等数学里的知识.但通过函数在某点处的增长速度来比较大小确实是一种创新解法,学生易接受. 在函数与导数教学与学习的过程中,对一些难题,应微专题分析,引导学生观察发现问题,不断创新解题方法,进而培养学生的探究与创新精神.Z2 观察发现问题,不断创新解法,培养创新能力
2.1 观察发现1
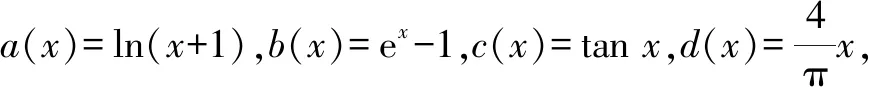
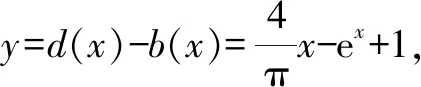


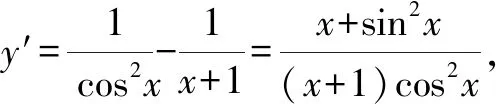
2.2 观察发现2
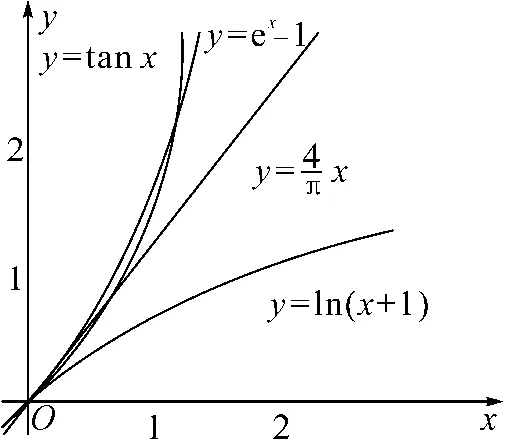
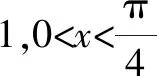
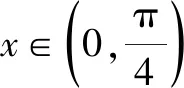
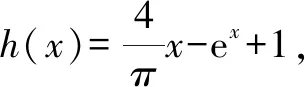
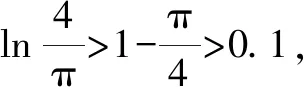
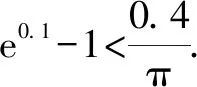
2.3 观察发现3
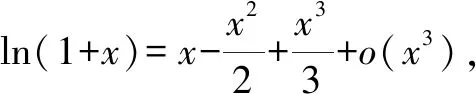
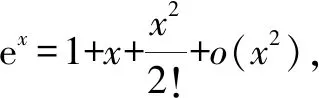
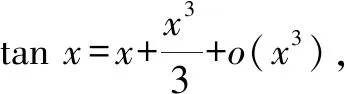
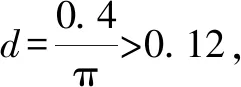
2.4 观察发现4
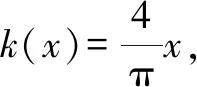
3 巩固提高
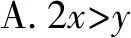
4 结束语
