路面不平度统计特性的改进
2023-02-11高雄GAOXiong
高雄 GAO Xiong
(福建华威钜全精工科技有限公司,福州 350001)
0 引言
国际和国内均采用幂指数作为描述路面不平度统计特性的标准形式,并给出了具体表示形式和相应参数[1-3]。
关于应用路面不平度统计特性标准形式的问题,目前国内外已经开展了大量的研究[1-4]。文献[1]基于汽车固有振动频率和行驶速度对路面不平度值进行了研究,采用C级路面不平度的功率谱,在时域内分析了与设定的功率谱密度吻合性问题。文献[2]在时域内建立了一个能反响路面激励与转向输入的联合模型,研究了在路面激励与转向耦合条件下的车辆侧倾状态问题。文献[3]阐述了时域内,从数学上描述路面激励的重构方法,推导了该方法的实现过程。
综上所述,在频域内国内外一致采用路面不平度统计特性开展相应的研究工作,在时域内国内外并没有采用与路面不平度统计特性对应的积分白噪声方法。因此,有必要在理论上对其进一步的研究和完善。本文针对路面不平度统计特性标准形式存在的不足进行研究,提出对路面不平度统计特性描述的完善思路。
1 路面不平度的统计特性
1.1 路面不平度空间功率谱密度描述
为便于研究,本文基于平稳随机过程,对路面不平度空间功率谱密度的构建以幂指数形式来描述,具体公式为[1]:
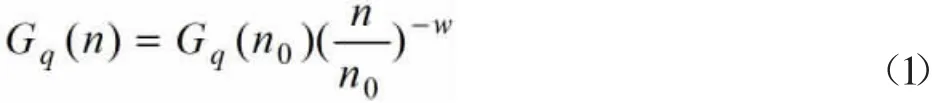
式中,Gq(n)——路面不平度功率谱密度;
n——空间频率,单位为m-1;
n0——参考空间频率,n0=0.1m-1;
Gq(n0)——参考空间频率n0下的路面不平度功率谱密度值,单位为m3;
W——频率指数。
1.2 路面不平度的均方根值
由随机振动理论可知,根据变量x的功率谱密度可得变量x的均方根值σx,即[1-2]

式中,Gx(n)——变量x功率谱密度。
由式(2),路面不平度均方根值为

式中,nl——空间频率的下限;
nu——空间频率的上限。
将式(1)代入式(3),并令W=2,得
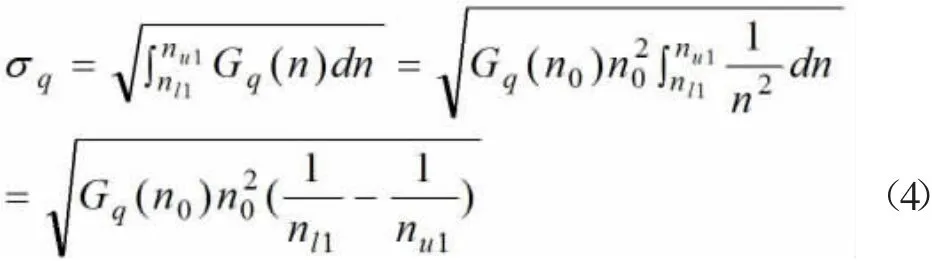
当空间频率取为标准给定的(0.011,2.83)时,由式(4)计算可得到与表1给定相同的路面不平度均方根值。
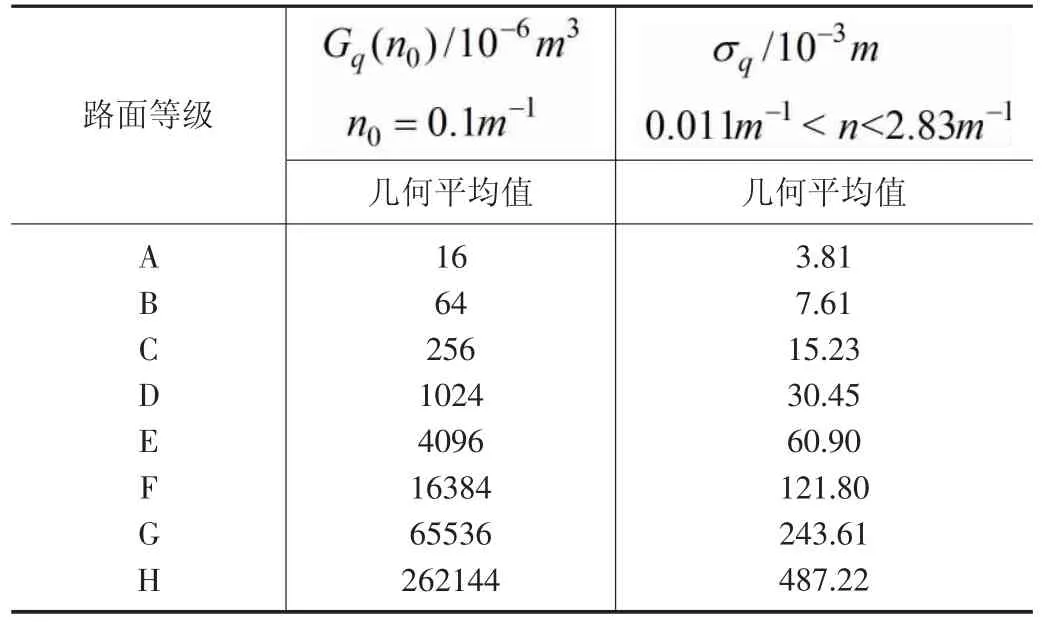
表1 路面不平度8级分类标准
2 路面不平度统计特性的改进
2.1 路面不平度空间功率谱密度描述的改进
式(1)中,当n趋于0时,Gq(n)在理论上是可以趋于无穷大,实际上并非如此。为解决这一问题,可以引入空间下截止频率的nq,将式(1)改进为

2.2 改进形式的均方根值
由式(5),取空间频率范围为(nl2,nu2),可得对应改进形式的路面不平度均方根值,即

3 空间下截止频率的构建
3.1 构建空间下截止频率的方程
假定式(4)与式(6)相等,有
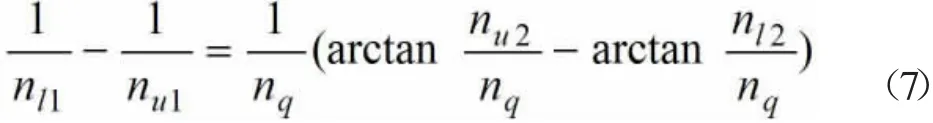
如果令nl1=nl2,nu1=nu2,则式(7)变为
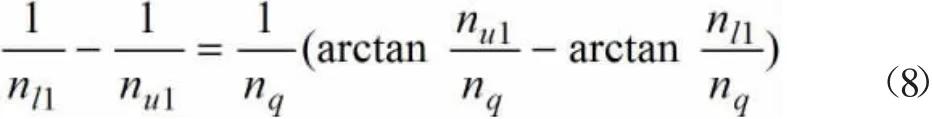
假定标准和改进两种形式的空间频率范围相同,并当式给定的空间频率范围为(0.011,2.83)时,式(8)变为

由式(9),可确定空间下截止频率nq。
3.2 空间下截止频率的数值求解
为了确定nq的最大值,将式(9)变为

nq值取0.01,0.001,0.0001,代入式(10)计算,将结果与0相比,具体如表2所示。

表2 nq不同取值时方程的误差
令空间频率范围为(0.011,2.83)且nq值取0,0.01,0.001,0.0001,通过式(4)和式(6),计算所得结果如表3所示。
由表3及图1可知,取nq=0.0001时,路面功率谱密度改进、标准的均方根值和功率谱密度吻合很好。因此,关于空间下截止频率nq可值确定为0.0001是正确的。
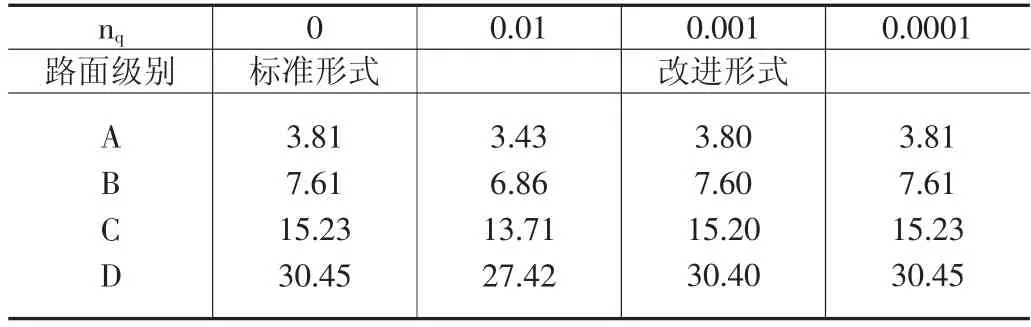
表3 nq不同取值时路面不平度的均方根值10-3m
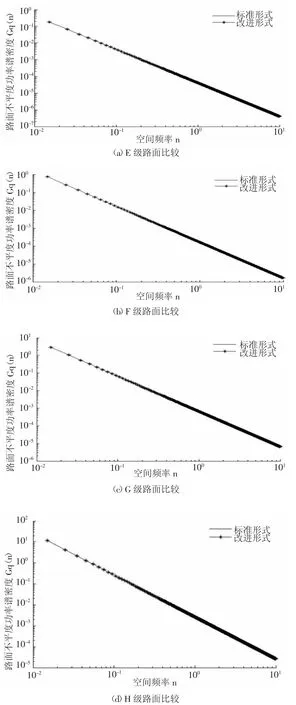
图1 nq=0.0001时改进与标准形式的对比
4 路面不平度统计特性改进的应用
4.1 汽车1/4两自由度系统
如图2所示的1/4汽车两自由度系统模型,其力学运动方程为
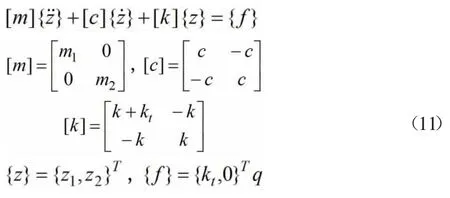

图2 1/4汽车两自由度模型
4.2 系统的频率响应特性
由式(11)可得各质量垂直位移对于路面随机激励函数的系统频率响应特性(矩阵)

4.3 振动响应量的频率响应特性
根据傅里叶变换的性质,振动响应量对于路面激励的频率响应特性为
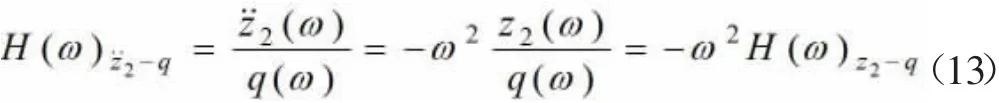

4.4 应用实例
为说明路面不平度统计特性改进形式对汽车振动响应的有效性,以某轿车为研究对象,其参数为,m2=878.8,m1=106kg,k=184082N/m,c=3292.8998Ns/m,kt=762900N/m。路面设定B级路面,以10km/h为增量,从10至60km/h的车速匀速行驶,分别取nq=0,0.01,0.001,0.0001进行仿真,仿真结果如表4所示。
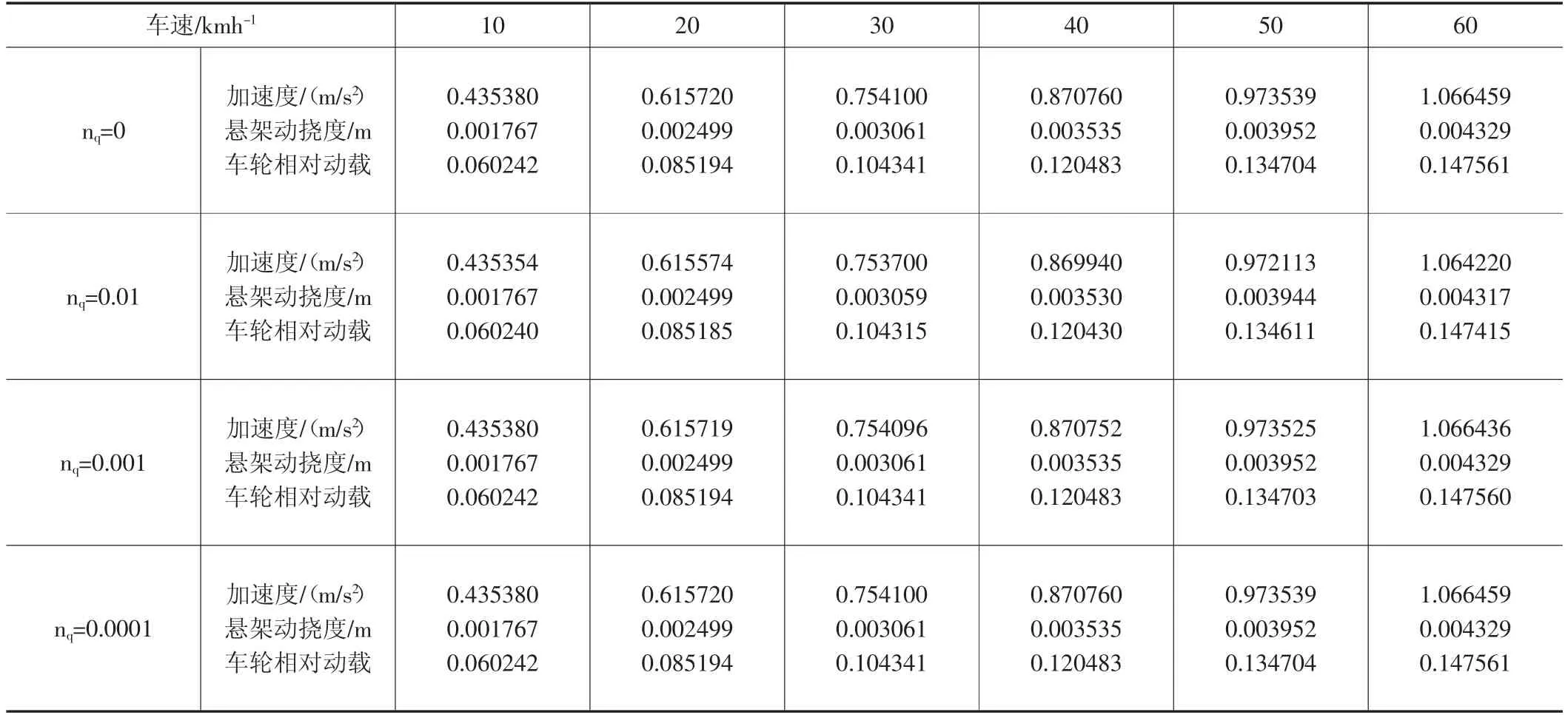
表4 人体座椅垂直加速度均方根值频域与时域仿真比较
由表4可以看出,在nq=0和0.0001时,各个车速下的身垂直加速度、悬架动挠度和车轮相对动载完全相同,说明nq=0.0001时,路面不平度统计特性的标准形式和改进形式的结果完全相同。
5 结论
①路面不平度的统计特性标准形式,在理论上存在不完备性问题,引入空间下截止频率构造路面不平度的统计特性改进形式后可以解决这一问题。②两种形式的均方根值对比,验证了确定的空间下截止频率的正确性;通过空间下截止频率取不同值时1/4汽车两自由度系统振动响应量均方根值对比,验证了确定的空间下截止频率的有效性。
