基于LS-DYNA的砂岩动静组合SHPB数值模拟
2023-02-09王军祥赵硕龙马宝龙
王军祥,赵硕龙,孙 港,黄 磊,马宝龙
(沈阳工业大学 建筑与土木工程学院,沈阳 110870)
21世纪以来,国家基础建设发展迅速,工程数量剧增,近年来国家也提出了向地球深部进军的发展方向,深部工程迎来了前所未有的建设发展高潮.深部工程中,岩石在受到爆破、冲击、卸荷等扰动作用之前,已经承受了高地应力,这种地应力对岩石变形破坏影响巨大,是不可忽略的.由于受力状态的不同,单一静、动载作用下岩石的变形破坏特性、强度准则已经不适用于深部岩石,无法解释深部工程灾害发生机理.
SHPB是岩石动力学试验最常用的方法之一,能够很好地还原部分深部岩石的受力状态,且静、动荷载的取值范围能够满足绝大多数工程要求.基于深部岩石受力状态,李夕兵等[1-2]首次提出了动静组合加载理论,并通过多年的研究,研制出一系列SHPB动静组合加载装置,为SHPB动静组合加载理论与试验装置的发展做出了突出贡献.但SHPB冲击试验过程极短,存在着重复性低、数据难以获取等问题,而数值模拟则可以很好地解决这些问题.高科[3]比较全面地介绍了常规SHPB数值模型的构建、分析全过程,总结了模型基本参数的经验取值.江松等[4]考虑了接触类型对模拟结果的影响,针对特定类型岩石,对接触类型的选择进行了经验总结.张明涛等[5]建立了一维动静组合SHPB数值模型,采用微裂纹密度法定义了损伤变量,此外杨英明等[6]、闻磊等[7]也考虑了损伤因素.周红套等[8]利用FLAC3D软件进行三维动静组合SHPB数值模拟,分析了围压对于红砂岩破坏模式的影响.Tan等[9]利用颗粒流方法对带有层理面的煤进行动静组合SHPB数值模拟.但由于动静组合加载理论还处于发展阶段,多维SHPB试验数据较少,数值模拟方面大多数也仅限于常规SHPB加载,缺少多维动静组合模拟与实际多维动静组合试验相呼应.因此,本文利用显式动力学LS-DYNA软件进行动静组合SHPB模拟,以轴压和围压为变量,研究其对砂岩力学特性、破坏形态及能量演化规律的影响,以期为动静组合SHPB数值模拟研究提供参考.
1 数值模型的建立与验证
1.1 SHPB基本原理
SHPB是研究材料动态力学特性最常用的方法之一,SHPB试验装置由冲击发射装置、入射杆、透射杆、试样、吸能装置组成.为了实现动静组合加载,研究人员在常规SHPB装置基础上添加了轴压、围压加载系统,典型的SHPB动静组合加载装置[10]如图1所示.
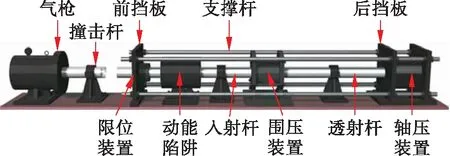
图1 典型SHPB系统装置示意图
SHPB常用数据处理方法为三波法,其计算公式为
(1)
(2)
(3)
式中:σs(t)和εs(t)分别为岩石试件的应力和应变;σI(t)、σR(t)、σT(t)分别为入射杆、反射杆、透射杆应力;ρ0、C0分别为弹性杆的密度和应力波在弹性杆中传播的速度;t为冲击应力波持续时间;Ls为试件长度.
能量是岩石发生变形破坏的本质.SHPB系统能量计算公式为
(4)
(5)
(6)
式中:A为弹性杆横截面面积;E为装置杆件的弹性模量;下标I、R、T分别代表入射、反射、透射信号.
1.2 数值模型建立
本次模拟中,入射杆长2 m,透射杆长1.8 m,试样直径、长度均为50 mm.图2为模型总体图,其中,弹性杆轴向网格尺寸为10 mm,沿圆周划分16格;砂岩沿轴向划分70格,沿圆周划分120格.
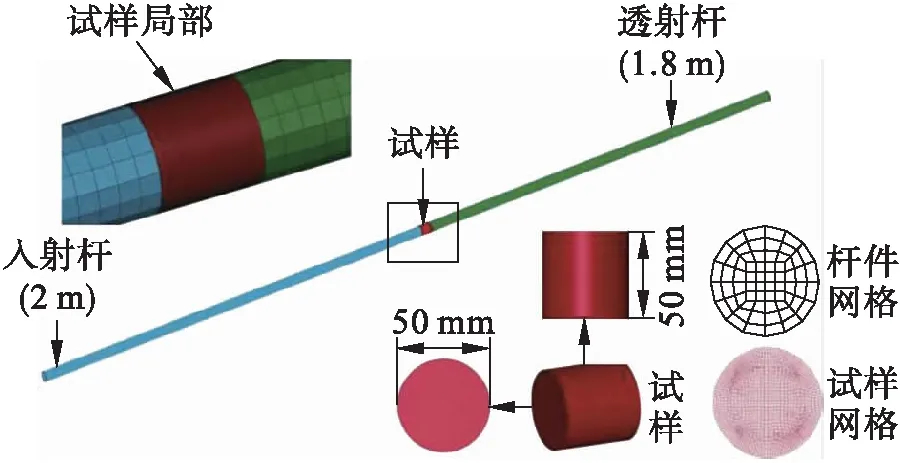
图2 模型总体图
单元类型选择单点积分常应力六面体单元,沙漏控制参数保持默认;接触类型选择面面侵蚀接触,接触罚函数刚度因子取2.0.表1、2分别为砂岩、弹性杆基本力学参数.砂岩本构关系选择HJC模型[11].为了产生单元失效,取砂岩最大主应变为0.006,模拟时间为1 ms,输出间隔取2×10-5s.

表1 砂岩静态力学参数
本次模拟中,结合砂岩的物理力学性质[12],动态荷载峰值取190、200、225、250、275、300 MPa,轴压取0、20、40 MPa,围压取0、2、4、6、8 MPa.

表2 弹性杆力学参数
1.3 数值模型正确性验证
本次模拟中输入应力波采用半正弦波,李夕兵等[1-2]通过试验验证半正弦波是SHPB试验的理想加载应力波形,可以极大消除波形弥散效应.高科[3]通过模拟研究发现,相比于矩形、钟形应力波,半正弦形应力波可以更好地实现试样早期应力应变均匀化.
本次模拟中压杆应力波及砂岩试样应变率曲线如图3、4所示,入射波为半正弦波,反射、透射波曲线形态良好.反射波存在近似平台段,且应变率在一定区间内保持恒定,由此可以确定本文所建立数值模型可以实现恒应变率加载.
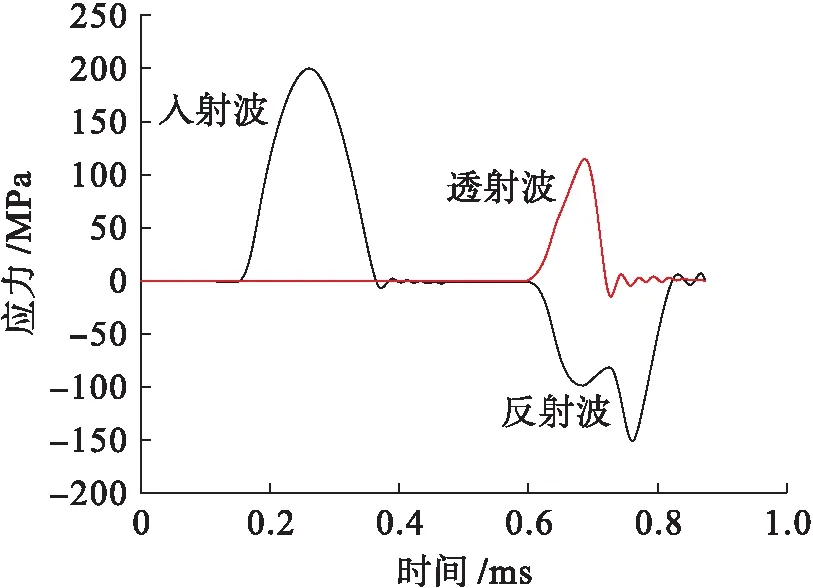
图3 典型应力波曲线
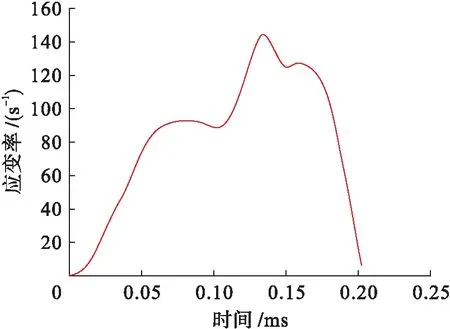
图4 恒应变率加载曲线
图5、6为同一截面单元和不同截面单元对应的应力波曲线.由图5、6可知,同一截面不同位置及不同截面的应力波曲线几乎没有差别,说明本文所建立数值模型弥散效应可忽略,满足一维应力假定,具有一定的正确性.
图5 同一截面单元及应力波曲线
图6 不同截面单元及应力波曲线
2 不同应力状态下SHPB数值模拟
2.1 常规动态SHPB模拟
2.1.1 应变率对砂岩力学性能的影响Ⅰ
常规动态SHPB模拟中,随着应变率的增加,砂岩动态抗压强度不断增加,说明砂岩强度具有率效应,近似呈线性规律,如图7所示.最大应变不断增加,应变率为77.5 s-1时,砂岩发生应变回弹.这是因为应变率较小时,砂岩发生局部掉块而非整体破坏,仍具有较强的承载能力,外界所做功一部分以弹性能的形式储存在砂岩中,砂岩破坏后,当应力卸载至低于砂岩内部弹性力时,发生应变回弹.
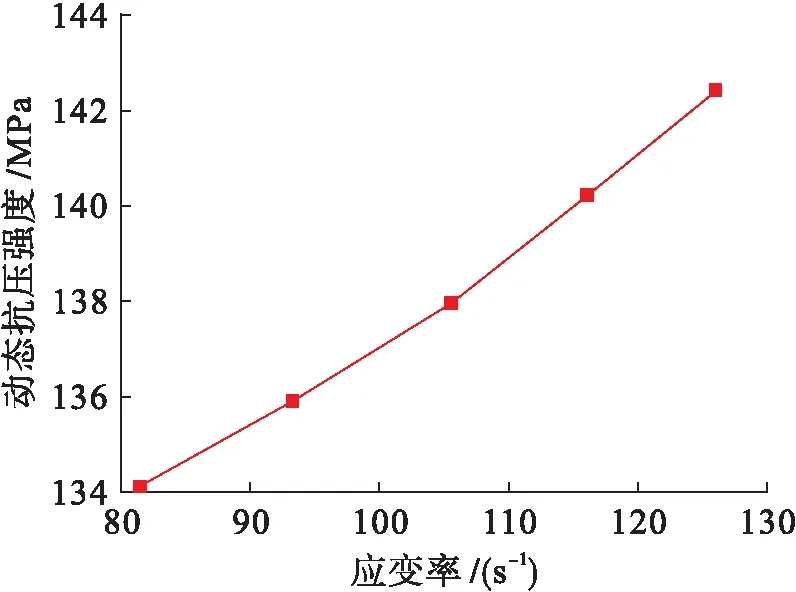
图7 动态抗压强度应变率曲线
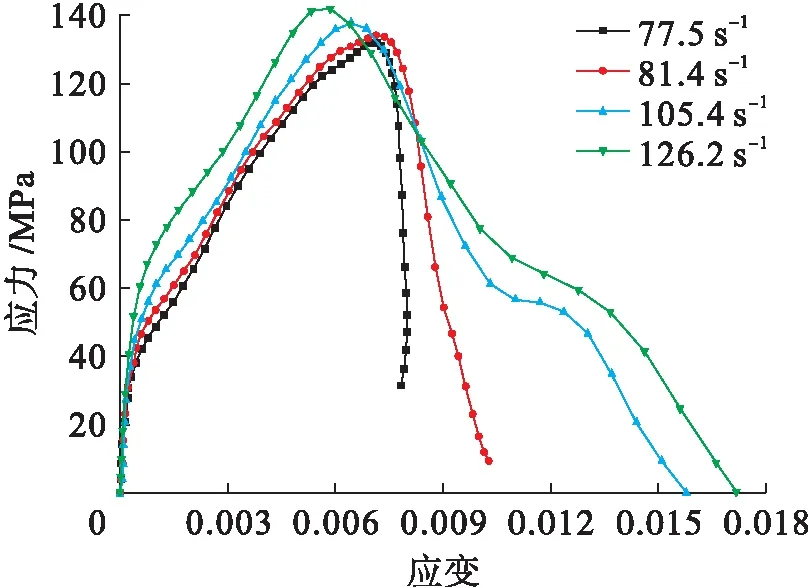
图8 不同应变率下应力应变曲线
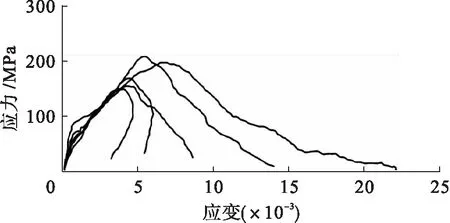
图9 实际试验数据曲线
2.1.2 应变率对砂岩能量演化特性的影响Ⅰ
随着加载应变率的增加,系统入射能、反射能均不断增加,近似呈线性关系;透射能不断减小,近似呈指数关系;耗散能不断增加.这是因为应力波传播到裂缝处时发生反射,应变率越大,裂缝数量越多,砂岩破坏程度越大,导致反射作用增强,透射作用减弱,同时更多的能量用于裂缝扩展和损伤累积.图10为系统能量随应变率变化曲线.
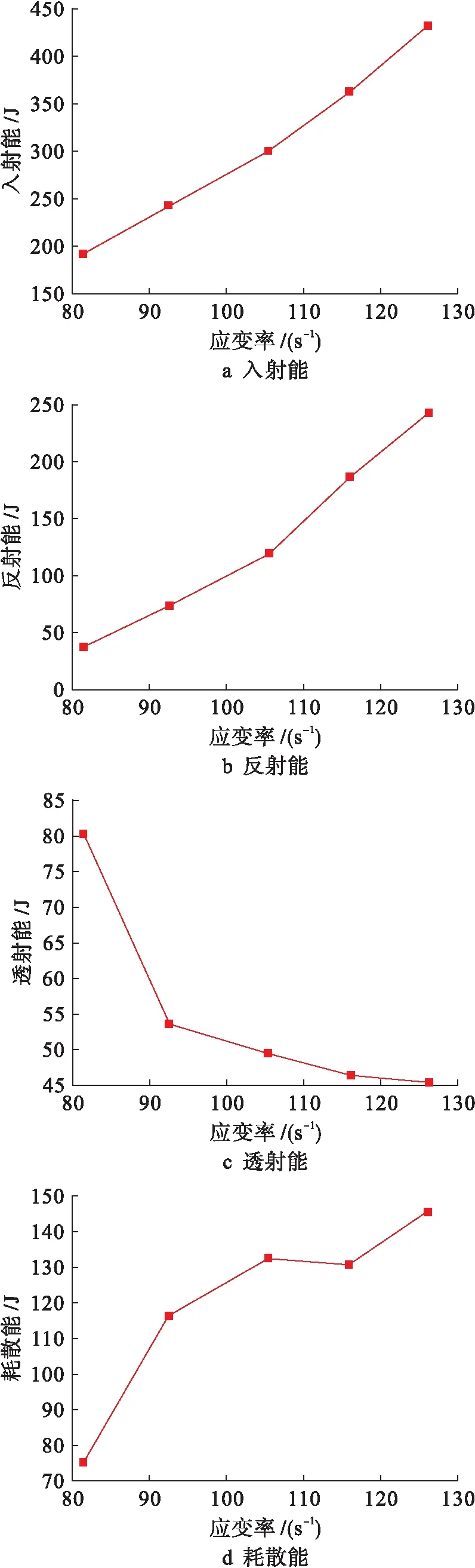
图10 系统能量变化曲线Ⅰ
耗散能与入射能的比值也可以视作岩石破坏过程中的能量利用率.从破岩的角度分析,同一能量基数时,能量利用率越大说明更大比重的能量用于岩石的损伤破坏,岩石破坏程度自然越大.图11为砂岩能量利用率随应变率变化曲线.随着应变率的增加,能量利用率先增加后减小,应变率为92.5 s-1时,达到峰值47.7%.
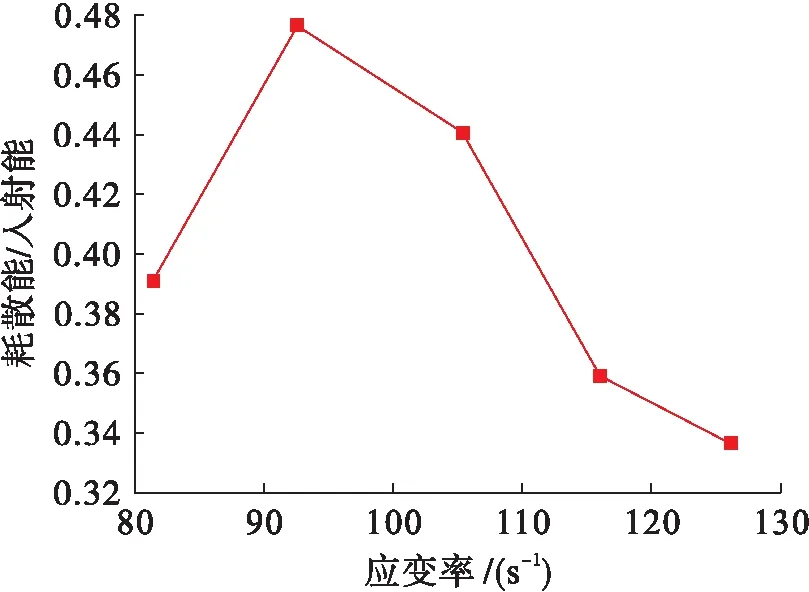
图11 能量利用率应变率曲线Ⅰ
2.1.3 应变率对砂岩破坏形态的影响Ⅰ
应变率为77.5 s-1时,系统能量基数较小,用于裂隙扩展、损伤累积的能量更少,所以砂岩发生局部掉块破坏,非整体破坏.应变率为92.5 s-1时,能量基数变大,但大多数耗散能用于轴向主裂纹的扩展,其他裂纹较不发育,砂岩发生轴向劈裂拉伸破坏.应变率为105.4 s-1时,试样端面冲击压力较大,单元正应力已超过某一限值,使得砂岩中的剪应力大于剪切强度,发生压剪破坏.应变率为126.2 s-1时,耗散能较大,裂纹扩展数量较多,砂岩损伤程度加剧,破坏程度较大,破坏形态为压碎破坏.图12为不同应变率下砂岩最终破坏形态图.随着应变率的增加,试样的破坏模式经历了局部掉块破坏、轴向劈裂拉伸破坏、压剪破坏和压碎破坏4个阶段.

图12 砂岩破坏形态
2.2 一维动静组合SHPB模拟
2.2.1 应变率对砂岩力学性能的影响Ⅱ

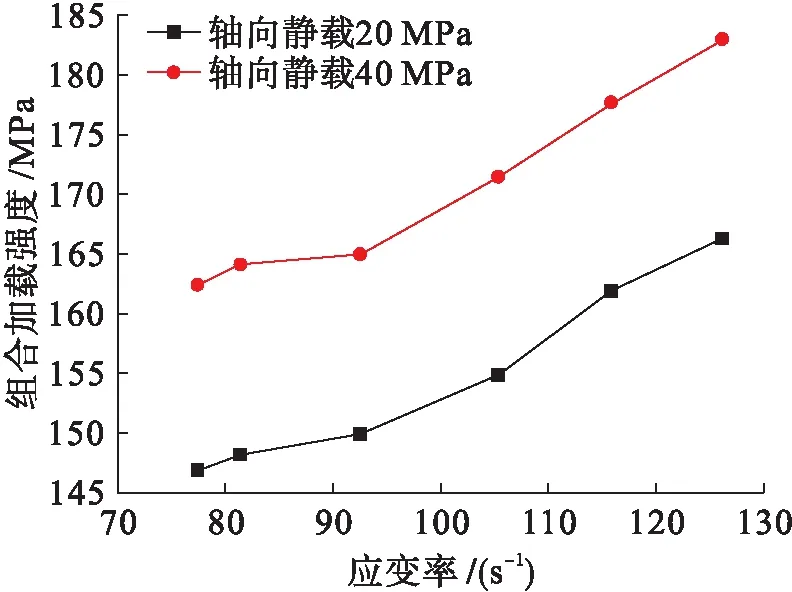
图13 组合加载强度应变率曲线Ⅰ
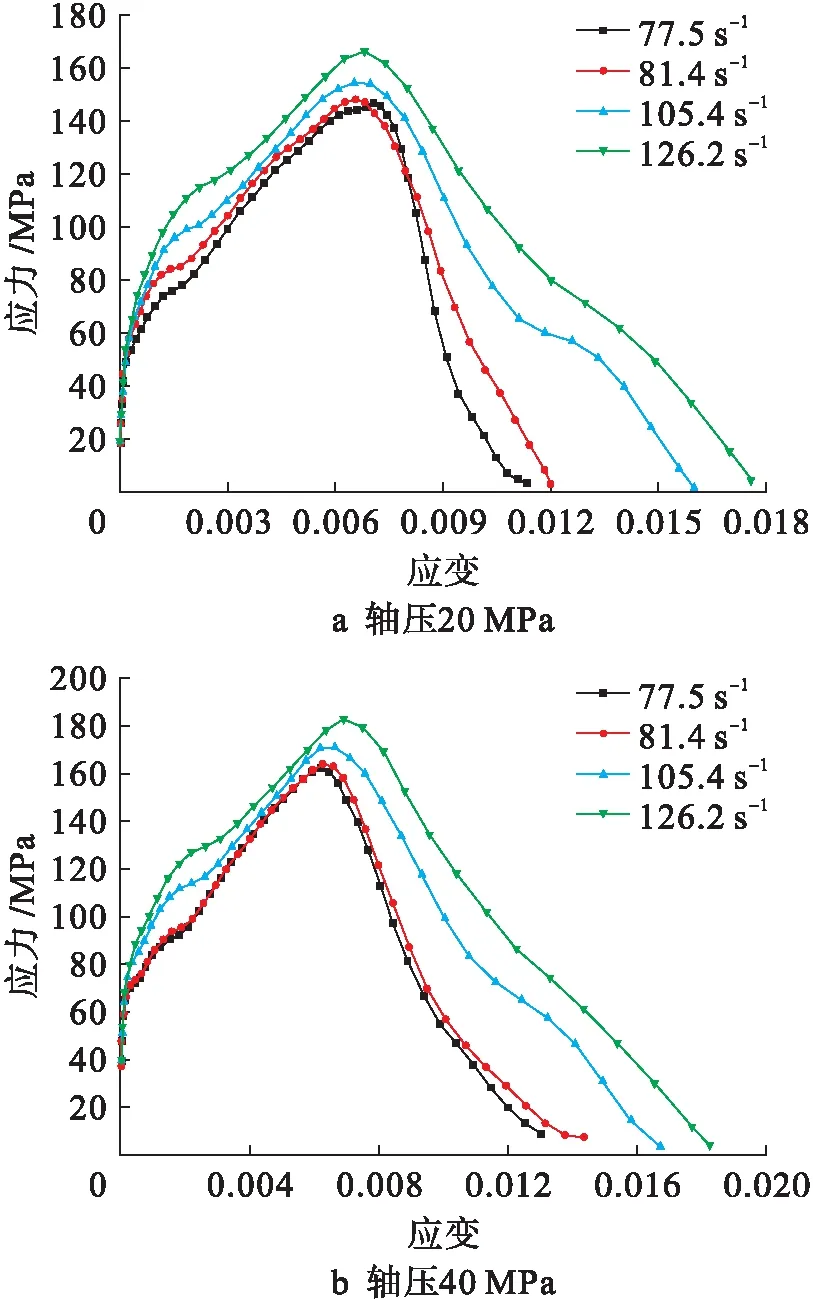
图14 不同轴压应力应变曲线
2.2.2 应变率对砂岩能量演化特性的影响Ⅱ
系统各能量变化趋势均同常规动态SHPB模拟.但同一应变率下,随着轴压的增加,入射能、反射能、耗散能均有提升;透射能不断降低,如图15所示.这说明轴压的存在能够提高砂岩的破坏程度,相比于单一静、动载,组合加载能够提高破岩效果.
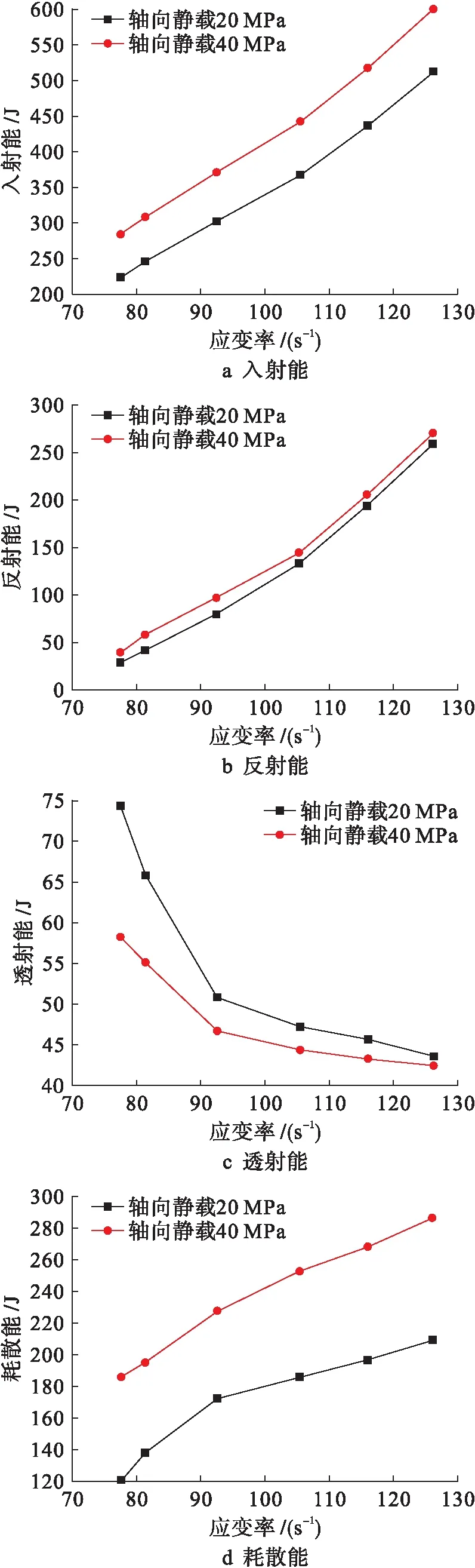
图15 系统能量变化曲线Ⅱ
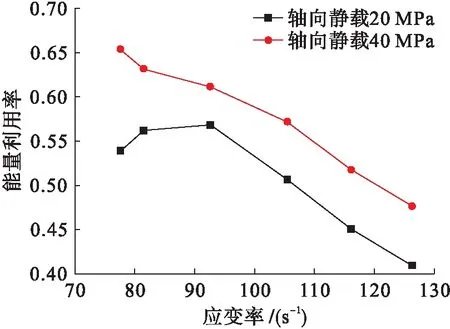
图16 能量利用率应变率曲线Ⅱ
2.2.3 应变率对砂岩破坏形态的影响Ⅱ
图17、18为砂岩破坏形态图.轴压为20 MPa时,随着应变率的增加,砂岩的破坏模式由初始的局部劈裂破坏发展为轴向劈裂拉伸破坏,最终演变为压碎破坏.轴压为40 MPa时,破坏模式由初期的压剪破坏发展为压碎破坏.轴压的增加意味着砂岩单元正应力增加,剪应力也随之增加,当砂岩内部剪应力达到其抗剪强度时,发生剪切破坏.而轴压较小时,由于泊松效应的存在,受压时岩石发生侧向膨胀,由于没有侧向约束,且岩石本身抗拉强度较低,故易发生沿轴向拉破坏.
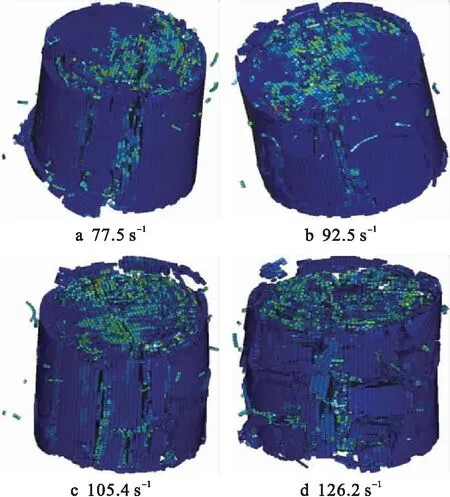
图17 轴压20 MPa砂岩破坏形态

图18 轴压40 MPa砂岩破坏形态
2.3 三维动静组合SHPB模拟
2.3.1 应变率对砂岩力学性能的影响Ⅲ
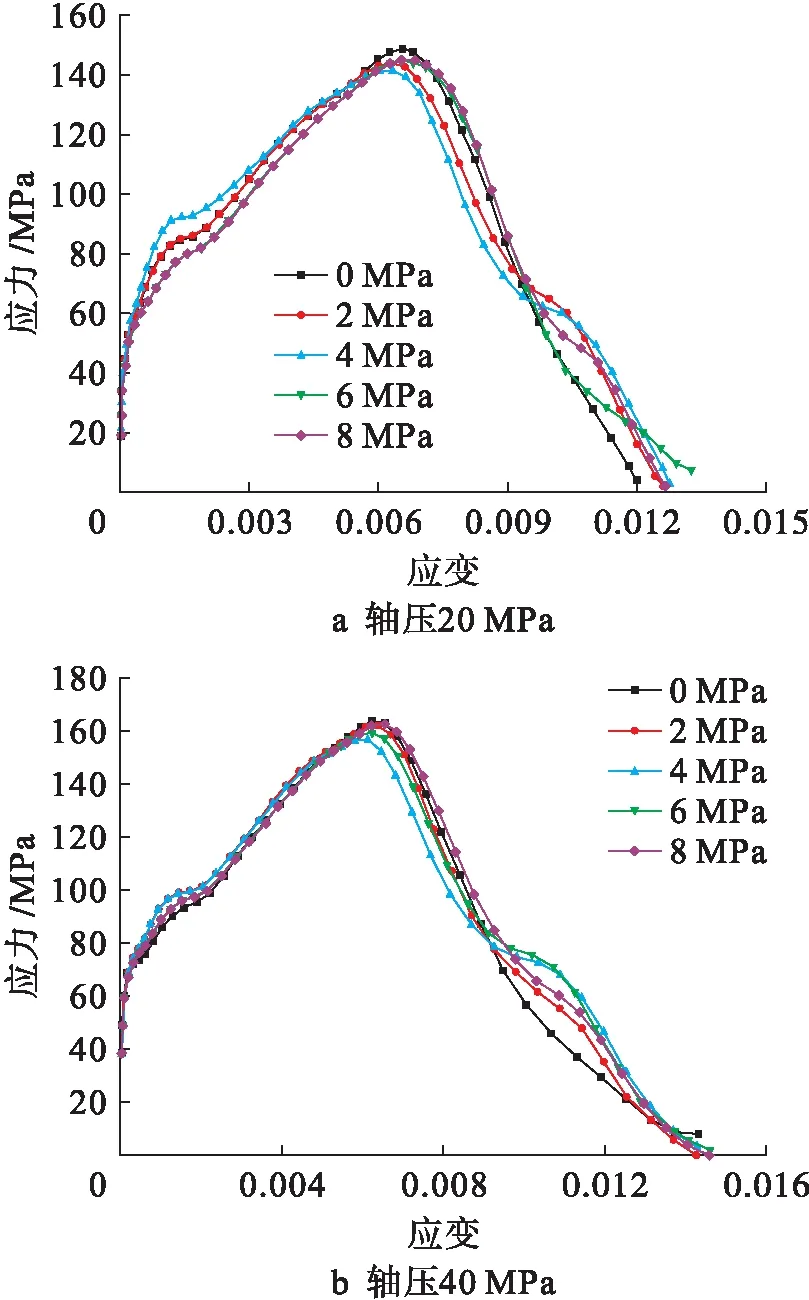
图19 不同围压对应的应力应变曲线

图20 组合加载强度应变率曲线Ⅱ
2.3.2 应变率对砂岩能量演化特性的影响Ⅲ
三维动静组合模拟中,系统各能量变化趋势均同常规动态SHPB模拟.在同一应变率下,随着围压的增加,入射能不发生变化,反射能不断减小,透射能先减小后增大,耗散能不断增大.这也表明围压较低时,围压更多起到促进微小裂隙扩展作用,而当围压增大到6 MPa时,围压对砂岩变形约束作用更大.图21为三维动静组合模拟中系统各能量与应变率关系图.
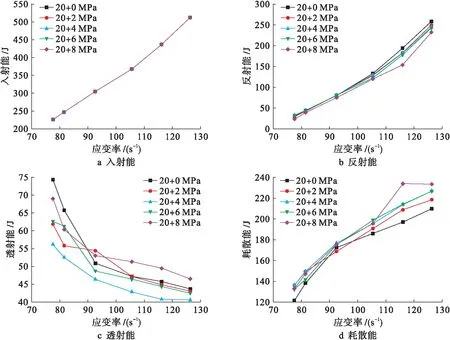
图21 系统能量变化曲线Ⅲ

图22 能量利用率应变率曲线Ⅲ
2.3.3 应变率对砂岩破坏形态的影响Ⅲ
无围压时,砂岩发生轴向劈裂拉伸破坏,随着围压的增加,砂岩侧向约束作用增强,伴随轴向裂纹生成的同时,垂直于砂岩轴向的裂纹也不断发展,当围压增大到6 MPa时,试样已经发生了明显的上下错动破坏,并且随着围压的不断增大,错动位移越来越大,直到试样发生整体断裂.
图23为不同围压作用下砂岩破坏形态.随着围压的不断增加,砂岩分别出现轴向劈裂拉伸破坏、层间错动破坏和压碎破坏3种破坏模式.

图23 不同围压下砂岩破坏形态
3 结 论
本文针对深部工程岩石动静组合受力状态,开展砂岩动静组合加载数值模拟,以轴压和围压为变量,分析了不同应力状态下砂岩变形破坏、能量演化特性,得出以下结论:
1)轴压比小于0.4时,无论处于何种受力状态,砂岩强度均表现出线性率效应,系统各能量变化趋势不发生变化.
2)轴、围压对于能量利用率影响规律较为复杂,轴压较低时,能量利用率存在峰值,轴压较高时持续下降.围压使得能量利用率出现一定波动,但总体上呈下降趋势.
3)轴压和围压对砂岩发生压剪破坏和层间错动破坏有一定促进作用,且荷载水平越大、数量越多,砂岩破坏表现出的延性越强.
