基于改进非线性自回归网络的洪水预测算法
2023-02-09崔雅博罗清元刘丽娜
崔雅博,罗清元,刘丽娜
(1.开封大学 信息工程学院,河南 开封 475004;2.河南省水文水资源局 站网监测处,郑州 450003;3.郑州大学 河南省超算中心,郑州 450001)
近年来,在我国频繁出现的反常降雨天气经常导致流域内发生各种自然灾害,其中洪灾的破坏力非常巨大,已经成为防灾减灾领域中关注的焦点.水文监测和预报预警是防御洪水灾害工作的重要环节.及时监测到流域内雨情变化信息并准确预测预报洪水,对有效运用防洪工程措施、制定正确的防御决策和减少灾害损失具有重要的指导意义[1-3].由于影响洪灾的因素有很多,简单的模型不能进行准确预测,为了最大限度降低突发洪水给人们造成的财产损失和生命威胁,专家们对洪水预测模型和方法的研究逐渐增多[4-5].刘志飞[6]采用最小二乘支持向量机的方法建立了洪水预测和预报框架,通过流域内水位的变化趋势对洪水灾害的发生进行预测,取得了不错的效果;段生月等[7]将正则化GRU神经网络融合到洪水预测框架中,从而解决了传统神经网络对洪水预测准确度不高的问题;王占明[8]运用灰色系统模型对海城未来可能发生大于或等于1 000 m3/s和2 000 m3/s的洪水进行预测分析,能够满足降雨产生地表径流的灰色特性,且预测精度较高;冯钧等[9]采用被研究流域内的大量历史水文数据建立了洪水灾害预测模型,并处理洪水流量水文时间序列,利用建立的模型对洪灾的发展态势进行快速预报.
由于时间序列具有随时间变化的特点,时间序列的完整建模一直面临着巨大的挑战.为了更好地表示时间序列数据,常将时间序列数据进行重置和筛选以便于模拟.Danandeh等[10]提出对原始时间序列数据进行平方根计算和归一化处理,来去除序列中的非平稳特征,但此方法在方便模拟时间序列数据的同时,也抑制了原数据的差异,从而降低了最终的预测性能;李文等[11]提出了一个处理时间序列数据的框架,对数据进行预处理,该方法虽然取得了较高预测性能,但人为手动计算过多,步骤较为繁琐;方方等[12]采用将小波变换与基因表达相结合的形式完善了时间序列数据的预测,提高了最终的检测精度.为了对洪水灾害进行更准确地预测,本文建立了一个具有外部输入的非线性自回归网络(nonlinear auto-regressive model with exogenous inputs,NARX),并将其与基于小波变换的数据预处理模块进行耦合,对时域和频域进行分析,利用多基因编程(multi-gene genetic programming,MGGP)进行特征选择,以获得信息丰富和无噪声的输入数据.利用栾川水文站近15年的水文数据对改进的NARX进行验证和测试,并与MLPNN算法、MGGP算法和原始NARX模型进行了比较,结果表明,本文提出的改进方法能稳定且准确地对洪水进行预测.
1 改进NARX的洪水预测算法
本文的改进思路是将小波变换(wavelet transform,WT)和MGGP集成到NARX中建立混合动态网络,从而实现对流域内洪水灾害的预测.
1.1 多层感知器神经网络
针对非线性问题,人工神经网络是一种常用的智能解决方法[13-14],其中多层感知器神经网络(multi-layer perceptron neural networks,MLPNN)是水文应用中最为流行的一种神经网络.图1为MLPNN典型的结构框图,大量的神经元在各个层之间相互连接.在输入层,一个神经元相当于一个预测器;在输出层,一个神经元可以代表一个响应.在隐藏层,神经元的数量取决于问题的复杂性.这些神经元中的信息传递都是不带任何一个循环的前向传播.
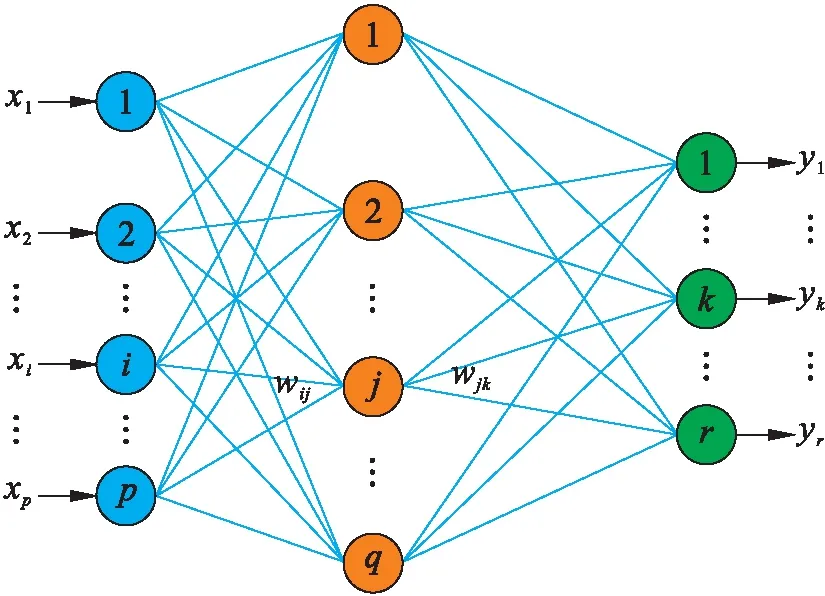
图1 MLPNN结构
1.2 多基因遗传编程
MGGP模型[15-16]是一种有监督的进化学习算法,其采用了适者生存的概念,线性结合了低深度基因编程(GP),并创建了一个简化适应度的解决方案.GP基因是一种树状结构的计算机程序,具有连接分支、根、内部和终端节点.图2为低深度基因编程.三级基因由1个根节点、3个内节点和4个终端节点组成,它们通过分支连接符(数学运算符)连接.
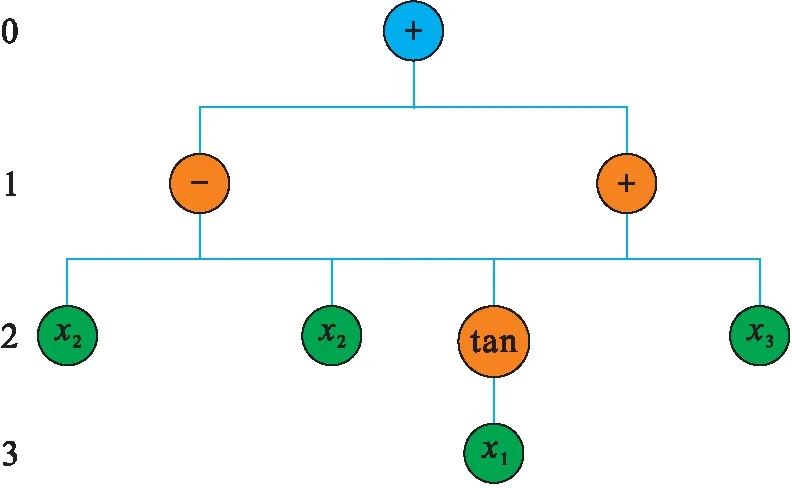
图2 低深度基因编程
MGGP方法的进化从染色体的产生开始,之后用染色体作为父母产生后代.这一过程涉及3种遗传操作:繁殖、交叉和突变.在繁殖过程中,父母仅仅通过复制自己来繁殖后代,因此不会产生额外的基因信息.在交叉过程中,两个新基因通过亲本之间交换材料产生.在突变过程中,用预定义的操作参数控制随机子树结构,从而产生一个新的基因.
MGGP模型中的主要开发过程包括:首先定义初始参数(函数集、种群大小、生成数、遗传操作率和最大基因数);然后生成一个基因种群,并创建一个解,再基于目标函数来检验模型的效率,使用遗传操作产生新的基因,如果不满足停止条件,重复最后一步;最后用低深度的GP基因构建出MGGP算法,其表达式为
(1)
式中:C为常数;ci为第i个基因Gi的权重;ng为存活的基因数;C和ci均由最小二乘法确定.
德国人把目光投向了一个数量庞大的人群,那就是全职妈妈。这些妈妈经过一定的培训,就成为了身兼母亲和护理员两职的可用人才。有关数据显示,目前德国1.1万多家养老机构的62万从业人员中,超过60%都是非全职的。在1.2万居家护理企业的27万从业人员中,非全职的比例甚至超过了70%,绝大部分都是全职妈妈。
1.3 小波变换
时间数据的基本信息通常隐藏在频域内,而在时域内并不容易获得[17].为了揭示时间序列的关键特征,通常会执行数据转换.傅里叶变换是最早使用的频率内容提取方法之一.但如果从时间域转换到频域,时间信息就会丢失.WT作为一种改进方法,可以同时捕获时间和频率信息.
WT产生了一个非平稳的时间尺度表示数据及其关系,从而揭示了数据的趋势、分解点和不连续性.具体来说,是将原始信号分解为低频和高频元素,并在时频域进行分析,这种处理技术允许检查原始数据中看不见的细节,从而提高数据挖掘模型的计算精度.WT被分为连续WT(continuous WT,CWT)和离散WT(discrete WT,DWT),主要区别是尺度参数的离散化方式.时间序列f(t)的连续小波变换WA,B(t)表达式为
(2)
式中:t为时间;Ψ*为小波函数或母小波Ψ的复共轭;A为膨胀(尺度)参数;B为平移(位置)参数.
在每个A和B上计算CWT系数会得到大量的数据.作为一种替代方法,DWT采用了缩放(低通滤波器)和小波(高通滤波器)函数,尺度和位置的值由两个参数所占权重决定,其计算过程为:通过低通和高通滤波器将时间序列数据分解为近似分量和细节分量,前者代表低频、高尺度分量,后者代表高频、低尺度分量,然后分别用低通和高通滤波器分析低频和高频内容.通过上述方式,将时间数据分为背景信息和有价值的琐碎属性信息.
1.4 改进的非线性自回归网络
改进的NARX是一个基于循环网络的模型,具体思路是将该模型与数据预处理模块相结合,并将预处理模块的输出作为外源输入,流程图如图3所示.
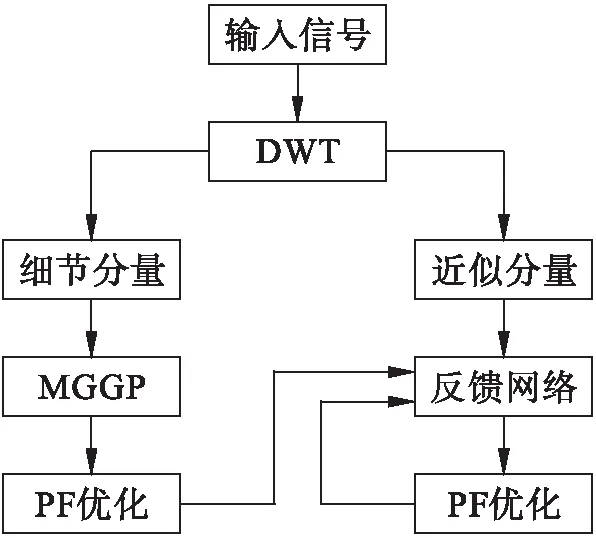
图3 改进的NARX流程图
该模型具体由3个阶段组成:
阶段一.由于DWT具有高计算效率和易于实现的特点,将输入的时间序列数据经过DWT,时间序列数据被分解成近似分量和细节分量,但并不是所有分解后获得的子信号都提供相同的信息.
阶段二.细节分量的子信号输入到MGGP,以消除可能干扰模型性能的冗余信息.MGGP生成一个显式表达式,表示对目标的贡献,MGGP此时被用作扩展细节的选择工具[18].由于其将GP树线性结合,仅提高基于目标函数的适应度,往往会产生复杂的进化解,这可能会导致出现水平膨胀和过拟合的情况.为了解决这一问题,采用了帕累托前沿(PF)方法来优化模型的精度和复杂性.具体流程为:首先限制最大的基因数量,以降低模型的复杂性和过拟合的风险,然后计算所有进化解的复杂度,并比较模型整体的复杂度和拟合度,最后平衡模型的准确性和复杂度,进而选择最佳模型中缩放后的细节分量.
阶段三.将近似分量和缩放细节分量作为非线性自回归网络的外部输入,这个动态网络由三层(类似于MLPNN)组成,该网络具有反馈功能,通过连接前面的输出形成反馈循环,使其具有多步预测特性,具体计算过程为
y(t-1),…,y(t-Δt2))
(3)
式中:y、a和ds分别为输出、近似分量和缩放细节分量;Δt1为输入延迟;Δt2为反馈延迟;F为函数符号.

2 实验结果与分析
本文实验均在同一个硬件平台上完成,平台设备为i5-9300HF处理器(主频2.40 GHz)和GTX1660Ti(显存6 GB)显卡.
2.1 评价指标
纳什效率系数(Ens)是评估观测值和预测值之间拟合程度的指标,可以用来验证预测模型是否达到最优.当Ens接近1时,表示当前的模型达到一个最优的预测状态,此时预测的估计值为一个理想的状态,可信度高;当Ens接近0时,表示估计的结果接近观测值的平均值水平,表示整体的结果较为可信;当Ens小于0时,则表示此时的模型是不可信的.通常将Ens大于0.75视为可信状态区间.Ens的计算公式为
(4)
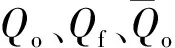
平均绝对误差(MAE)用来描述预测值与观测值之间绝对误差的平均值.均方根误差(RMSE)则用来描述模型值与观测值之间的差异,为所有绝对误差平方和的均方根.
2.2 实验设置
MLPNN是一个有监督的学习网络.预测值作为输入,当前观测值作为目标,本文采用LM算法对网络进行训练,然后将仿真误差反向传播,以调整网络的权值和偏差.该网络具有S型隐含神经元和线性输出神经元,通过试错过程获得最优的隐含神经元数量.本文将MAE设为适应度函数,如果训练达到最大值10 000个epoch或MAE低于阈值0.01时,则终止计算.其中,1个epoch指将所有训练数据全部训练一次,激活函数采用linear激活函数.
在MGGP模型中,基因的数量被限制为5个,每个基因的最大深度设置为4.初始种群规模为300代,最大代数为150代,适应度函数为RMSE.经过一系列实验,繁殖率、交叉率和突变率分别调整为0.3、0.86和0.15.
本文提出的改进NARX模型,其外部输入为水文时间序列数据的小波分解分量,因此需要选择适当的小波,本文采用了常用的Hear小波[20]作为外部输入的小波函数.与MLPNN类似,原始NARX网络和改进NARX网络均使用LM算法与MAE适应度函数进行训练;如果计算达到最大值10 000个epoch或MAE低于阈值0.01,则终止计算.
2.3 结果与分析
本文实验数据为栾川水文站近15年所测水文数据,其中按每天收集到的系列数据累计共3 425个,按8∶2的比例分为训练集和测试集.经过统计,低水位设定为2.8,高水位设定为6.9.对MLPNN、MGGP、NARX和改进NARX模型进行了评估和比较.针对MLPNN和MGGP两种模型,采用短期记忆结构来提高学习性能.针对改进NARX模型,则在原始NARX网络的基础上利用小波分解和对MGGP的尺度分析,并通过将前馈神经网络与非线性自回归模型相结合,为洪水预测提供了更稳定的预测模型.表1为不同模型的洪水预测结果.
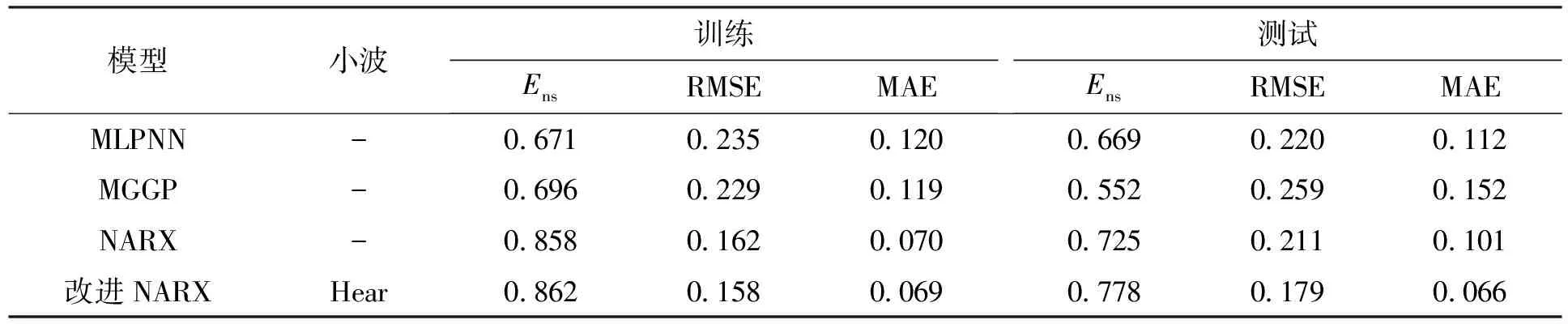
表1 不同模型的洪水预测结果
通过表1的对比结果可以看出,在训练时的Ens值方面,改进NARX的Ens值在3个模型中最高,达到了0.862,比可信区间的阈值0.75多了0.112,比其余三个模型MLPNN、MGGP、NARX分别高出了0.191、0.166、0.004,其中MLPNN的Ens值最低为0.671,小于可信区间的阈值0.75;同时改进NARX的RMSE和MAE值也小于其他3种算法,分别为0.158和0.069.上述结果说明在训练过程中改进NARX的拟合性能最好,误差最小.在测试的预测结果对比中,改进NARX同样达到了最好的性能,其中Ens值最高为0.778,远高于Ens值最低的MGGP模型,此外MGGP的测试Ens值要相对其他算法下降的幅度最大,说明MGGP的泛化能力相对较低.在误差方面,改进NARX的RMSE和MAE值在与其他3种算法的对比中仍然是最小的,分别为0.179和0.066,验证了改进NARX在洪水预测方面的有效性.
为了进一步直观地评估改进NARX的预测性能,本文使用了栾川水文站的流量水位数据进行了性能检测,以水位每日时间序列的形式对比了不同模型观测值与预测值,得到不同算法下的预测结果,如图4所示.
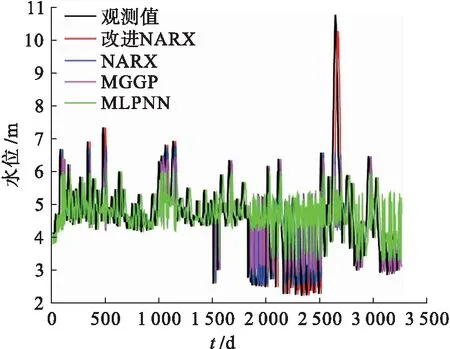
图4 不同算法对比结果
通过图4的对比结果可以看出:MLPNN、MGGP、NARX和改进NARX这4种模型都能够很好地捕捉水位值在4~6之间的时间变化.然而,在水位值接近7以及大于7时,或者在水位值低于3接近2的情况下,传统的3种模型都不能获得理想的预测值,且都在一定程度上低估了水位值.而本文方法引入了外部输入的改进NARX模型,能准确地预测水位值,即使在水位突变的情况下也能进行准确地预测,从而验证了改进NARX具有更强的洪水预测能力.
3 结 论
为了获得更加准确的洪水预测结果,本文建立了混合动态神经网络,该网络结合数据预处理模块,构建了一个具有外源性输入的非线性自回归网络.通过对水文数据进行小波变换,将其分解为一个低频的近似分量和一个高频的细节分量,利用MGGP模型处理高频分量消除了冗余信息,最后将两种分量输入NARX,从而得到更加准确的预测结果.利用栾川水文站收集的近15年期间的水文数据,对所提模型进行了评估,并与几种传统的机器学习方法进行了比较,实验结果表明,本文提出的改进混合动态神经网络能够对洪水灾害给出更加准确的预测结果.
