基于动态规划的多波束测线布设模型

王 楠，俞治丞，王景贤

（南京信息工程大学 大气物理学院， 南京 210044）

声波波束测深法是利用声波传播原理进行海水测深的常用方法，其原理为测量船换能器垂直向海底发射声波信号，并接收反射声波信号，利用发射波与反射波时间差实现海水测深。为了获得某一海域较为全面的深度数据，通常使用多波束测深法进行测量。多波束测深法一次发射数十乃至上百个波束，能测得以测量船测线为轴线且具有一定宽度的全覆盖水深条带。为保证测量便利性和数据完整性，相邻条带间应有10 %～20 %的重叠率。由于真实海底地形起伏变化大，若测线间隔布设不合理，易出现漏测，或因重叠率过高导致数据冗余量增大，影响测量质量和效率。本文针对2023 年高教社杯全国大学生数学建模竞赛（CUMCM）B 题给出的四个问题[1]，基于几何原理，建立了海底坡面多波束测深平面模型、变化测线方向的多波束三维覆盖模型、单目标规划模型和微元测线规划模型，探究不同海域情况下的多波束测线布设优化方案。

1 问题一模型的建立与求解

问题一设定与测线方向垂直的平面（以下简称为测线垂面）和海底坡面的交线构成一条斜线，其与海平面的夹角为α，要求建立多波束测深的覆盖宽度与相邻条带重叠率的数学模型，并求解特定位置覆盖宽度、重叠率等指标。

1.1 海底坡面条带覆盖研究

如图1 所示，由于海底具有一定坡面，可观察到的覆盖条宽度应为坡面覆盖长度在水平面上的投影。设可观察到的覆盖宽度为w，

其中，W 为坡面覆盖长度。若测线1 处海水深度为D1，测线2 处海水深度为D2，测线间距为d，则满足，

若线段AC 与BD 的长度分别为W11，W22，换能器夹角为θ，可通过解三角形得到测线1 覆盖区域与测线2 覆盖区域的重叠率为

根据三角关系，测线1 覆盖宽度为[2]

测线2 覆盖宽度的求解方法同测线1。

1.2 特定海底坡面条带覆盖求解

已知某特定海底坡面，其中心深度为D0=70 m，则根据1.1 模型，第i 条（i=-4，-3，…，4）测线的对应海水深度Di、覆盖宽度wi分别为

第i 条测线与第i+1 条测线（i=-4，-3，…，3）覆盖区域重叠率为

已知测线间距Δd=200 m，且ΔD=Δdtan α，代入已知数据即可求解得到该海域多条测线处海水深度、覆盖宽度与覆盖区域重叠率，计算结果见表1。

由表1 可以看出：测线间距为200 m 时，仅有0 m 与200 m 海域覆盖区域的重叠率满足10%～20 %的测量便利性与数据完整性条件；重叠率为负值表示存在漏侧。因此，在200 m 与400 m 海域间可适当减小测线间距d，使得其覆盖区域重叠率增大；在-800 m 与-200 m 海域间可增大测线间距d，使得其覆盖区域重叠率减小。

2 问题二模型的建立与求解

问题二中，测线方向与海底坡面法向在水平面上投影的夹角为β，要求给出特定β 取值下多波束测深的覆盖宽度。为便于研究，需要将问题一的平面模型扩展为三维立体模型。建立海底坡面的三维坐标系，如图2 所示。

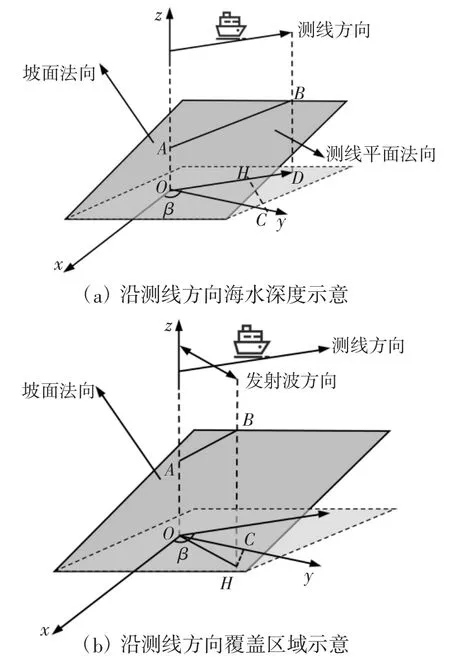
图2 海底坡面三维坐标系示意

2.1 沿测线海水深度变化研究

当测量船沿测线方向前进l 时，该路程中海水深度的变化量为

式中，γ1为测线垂面与坡面交线（图2 中线段AB）与海平面的夹角，可以通过解析测线垂面与海底坡面的法向量求得。若测线垂面法向量为海底坡面法向量为，那么γ1满足

2.2 测线覆盖区域分析

在三维坐标系下研究测线的覆盖区域时，需要作垂直于测线方向的平面，该平面即为发射波所在的平面，其与海底坡面的交线即为测线覆盖区域。若该平面在海底坡面三维坐标系下的法向量为则其与海底坡面的交线与海平面的夹角γ2可以表示为

γ2的意义与问题一中角α 的意义相似，则可将问题二的三维问题转变为海水深度沿测线变化的二维平面问题。通过对三维平面的解析，得到变化测线方向的多波束测深情况下覆盖宽度wm的表达式，

其中，D（β，l）为夹角为β 的测线行进路程l 时的海水深度，其变化量由公式（8）确定。

2.3 特定位置覆盖宽度求解

问题二需要求解β 的8 个取值，测量船沿测线方向运动2.1 海里，每间隔0.3 海里测量一次海底情况。当β∈（π/2，3π/2）时，在测线方向上海水深度逐渐减小；当β∈（0，π/2）∪（3π/2，2π）时，在测线方向上海水深度逐渐增大。已知l=0时的海水深度，可以对海水深度进行离散化分段求解，表达式为

进而得到在（iπ/4，iΔl）情况下的覆盖宽度的表达式为

将赛题给定的换能器夹角等已知条件代入上述公式，即可求解得到不同测线方向、不同船体位置情况下的覆盖宽度。由于海底为固定坡面，在各个测量方向上，覆盖宽度呈线性变化，并具有对称性特征，如图3 所示。

图3 覆盖宽度与测线方向、船体位置关系

3 问题三模型的建立与求解

问题三限定了一片南北长2 海里、东西长4海里的矩形海域，海底依然具有一定坡度，且西深东浅，要求设计满足重叠率条件、可以完全覆盖该海域的多条测线，并尽可能使测线长度最短。为便于测量海底情况和计算重叠率，尽可能确保不漏测，测线应均为直线[3]，且测区内的各主测线应为平行关系。

3.1 南北方向平行测线设计

为使得测线尽可能分布稀疏，直接考虑相邻两侧线之间重叠10 %的情况。先确定第一条南北向测线，使得测线条带覆盖区域左边界与矩形海域西边界完全重合。再以重叠率为10 %确定下一条测线。以此类推，从西到东设计出可以覆盖矩形海域、重叠率固定为10 %的多条测线（如图4 所示）。最后计算测线总长度。

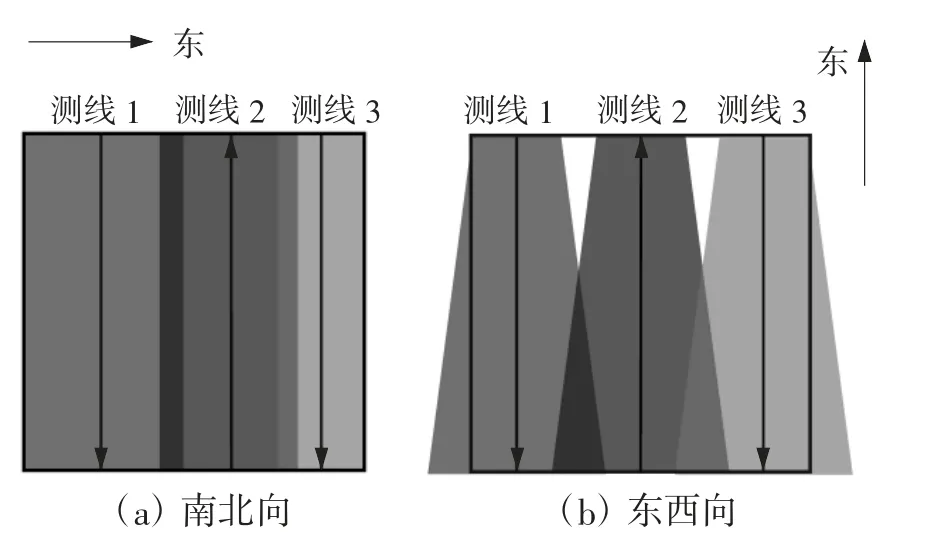
图4 测线条带覆盖示意

第一条测线对应坐标x0应与测线左覆盖区域长度一致，x0的表达式为

由于设定两条测线的覆盖区域重叠率为10%，根据重叠关系求解得到第一条测线的右侧坡面覆盖长度为

第二条测线的位置坐标为

同理，对于第i 条测线的坐标，可以得到迭代公式。再根据初值条件Dleft=110+2×1 852tanα，通过迭代可以得到第1 条到第n 条测线的坐标。

综上，动态规划求解模型为

根据上述计算，当两两测线的重叠率固定为10 %时，求解得到在南北方向上共需要设计34条测线，测线总长度为125 936 m。南北向平行设计测线时，覆盖率与测线条数呈线性关系，覆盖率越大，测线条数越多。因此，10 %重叠率情况下测线总长度最小。

3.2 东西方向平行测线设计

当船自西向东移动时，船体所在海域的深度越来越浅，覆盖宽度也越来越小，沿测线方向覆盖区域形状为梯形。在较深处，可能会重叠率过大，而在较浅处，则可能会漏测。当深度变化不大时，梯形趋近于一个矩形，深处与浅处的重叠率相近，在合理设计下可完全覆盖海域，且重叠率为10 %～20 %。

经计算，矩形海域西边界最深处海水的深度为Dleft=206.94 m，东边界最浅处海水深度为Dleft=13.06 m。借助问题二模型进行简单计算，可以发现在最深处只需设计6 条测线，而在最浅处则需设计高达上百条测线。测线数差别过大，必定会产生漏测与重叠率过高的情况。因此，所有测线呈东西走向是不合理的。与此类似，所有斜向平行测线设计也无法解决类似问题。

综上，该矩形海域最优布设策略为：南北向平行设计34 条测线，测线总长为125 936 m，测线具体布设如图5 所示。

图5 南北方向测线布设设计

4 问题四模型的建立与求解

问题四要求针对一个海底凹凸不平的实际海域进行测线布设设计。现已给出该海域（南北长5 海里、东西宽5 海里）的历史单波束测深情况。以此数据为基础，对该海域重新进行更为精确的多波束测深设计，并尝试求解测线布设的最优方案。

4.1 海域信息分析

若多条等深线近似平行，且相邻两条等深线的距离近似相等，则可认为这些等深线代表一个固定坡度的坡面。为简化问题，将近似相互平行且距离相近的多条相邻等深线归为一组，其对应的海域可近似为具有固定坡度的坡面。

依据所给单波束测深数据，绘制等深线图，并将该海域分成三个区域进行分析，如图6 所示。

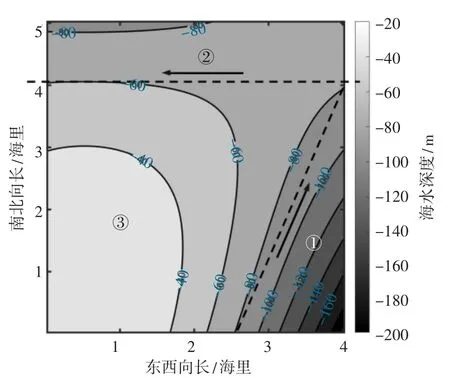
图6 按等深线分区示意

4.2 固定坡面区域①、②测线设计

区域①与区域②的等深线基本相互平行且两两相距较近，故可将这两个分区拟合成一个固定坡面。如图6，区域①可近似为一个直角三角形，即拟合出了一个上界为-80 m，下界为-197.20 m的坡面。根据问题三设计方案，沿等深线布设测线是最优方案。选取合适坐标点求解得到该拟合坡面坡度α1=0.046 2 rad。利用动态规划的求解思想，结合问题三模型与区域边界条件，可求解得到三角区域覆盖宽度的表达式。

区域①为三角形海域，按照上述算法会出现漏测区域。根据三角关系，求得漏测区域面积的表达式为

其中，ϕ 为测线与海平面的夹角。在区域①中，重叠率固定为10 %，存在一定的漏测率。通过上述分析，使用动态规划求解得到区域①测线总长度为32 098 m。

同理，将区域②拟合为北深南浅的固定坡面。区域②最优解为测线方向为正东正西、覆盖率恒定为10 %。由于区域②为矩形海域，则可直接利用问题三的模型进行求解，得到区域②测线总长度为66 672 m，且不会出现漏测区域。

4.3 基于微元法的区域③测线设计

由图6 可知，区域③的等深线具有一定折角，因此，不可使用固定坡度拟合方法简化处理。若要使得区域③测线设计尽可能优化，仍需使测线尽可能沿等深线分布。

区域③的右边界处等深线近似平行且间距较近，在该范围内进行固定坡面拟合，从所给数据中取点计算，可估算其大致坡度为0.054 rad。以-80 m与-60 m 之间的某等深线D0为起始位置，固定覆盖率为10 %，自东向西设计测线。

以等深线-D0在所给数据中筛选对应深度，得到等深线附近散点的集合，其中散点Pi的坐标为（xi，yi，zi）。由于散点间距极小，为方便后续计算，令各散点上测线方向均为正南正北向。在坡面固定为=0.054 rad 时，可求得Pi处覆盖宽度为

结合公式（19）、（20），可根据前一测线的估计坡度与大量散点坐标，确定下一测线的估计坡度与散点坐标，据此迭代直至结束。

初始位置的选择在该迭代过程中至关重要，使用遗传算法求解以下规划模型：

其中，j=0，1，…，n-1。

采用遗传算法[4]求解得最小测线下的最优D0为-75 m，该初始测线矩形覆盖区域的右边界恰好与-80 m 深度线重合，且未浪费覆盖空间。

图7 为区域③具体测线的走向。由图7 可看出，海水深度在东南方向较深，在西南方向较浅，符合等深线的走向。

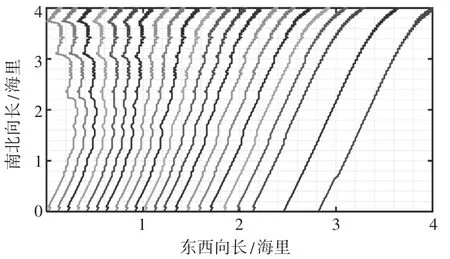
图7 区域③测线设计示意

在所得测线布设下，利用动态规划和基于遗传算法的微元法即可得最短测线总长为308 800 m。因为区域②为矩形且深度分布较为均匀，所以区域②为满覆盖情况，而区域③是微元法求解，误差很小，因此只需要计算区域①的漏测面积，即可得到漏测百分比，为0.211 9 %。由于区域②在区域下边缘处布设的测线覆盖宽度超出原有区域，与区域③重叠较多，而区域②测线为正东西走向，长度为4 海里。此外，区域①和③临界处覆盖率小于20 %，因此重叠率超过20 %部分的总长度即为区域②测线长度，为7 408 m。

综上，经计算得到测线总长度为308 800 m，漏测区域占总待测海域面积的0.219 9 %。表明在上述测线布设下近似满足全覆盖要求，重叠率超过20 %部分的总长度为7 408 m，仍有部分区域数据冗余，模型存在改进空间。