（3+1）维Korteweg-de-Vries方程的复合函数混合解

冀敏杰，套格图桑

（1.内蒙古师范大学 数学科学学院，内蒙古 呼和浩特 010022；2.内蒙古自治区应用数学中心，内蒙古 呼和浩特 010022）

孤立子是一类非线性发展方程的解，反映的是一类非常稳定的物理现象。1834年J.S.罗素在一篇报告中提到他观察到一种奇特的自然现象。1895年D.J.柯脱维格和G.德维雷斯研究浅水波时建立一个非线性波动方程（称为KdV方程）得出类似的解［1］。近年来，学者们利用贝尔多项式法［2］、广田双线性法［3］、有理函数变换法［4］、齐次平衡法［5］、Bäcklund变换法［6］等多种方法求解非线性发展方程，并获得了许多新的研究成果。

文献［7］应用试探函数法得到了（2+1）维广义KdV方程的周期孤波解，文献［8］基于贝尔多项式理论，通过符号计算得到类9阶KdV方程的有理解，文献［9］通过给定的符号计算法得到了一类（3+1）维KdV方程的有理解，文献［10］通过扩展的有理函数方法得到了（3+1）维变系数KP方程的lump解。

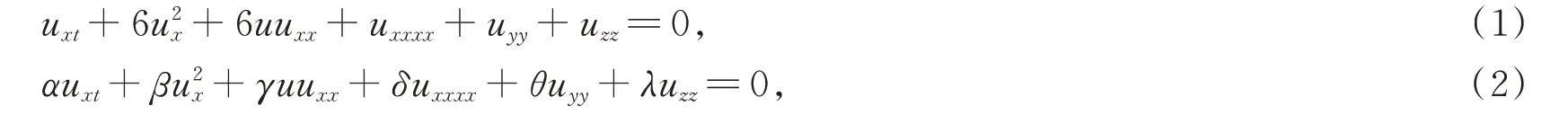
其中u是关于x，y，z，t的函数，x，y，z，t是独立变量，α，β，γ，δ，θ，λ均为常数。当取α=1，β=6，γ=6，θ=1，δ=1，λ=1时，方程（2）转化为方程（1）。

本文利用Hirota双线性法，把方程（2）化为双线性形式，通过运用试探函数法和符号计算系统Mathematica给出了包含方程（1）和（2）的（3+1）维KdV方程的lump新解以及三角函数、指数函数、分式函数、对数函数和双曲函数通过几种形式组合的复合函数新解。

1 （3+1）维KdV方程的exp-cos-cosh-sinh-sin型解

方程（2）在约束条件β=6α，γ=6α，δ=α下，通过变换

可转化为

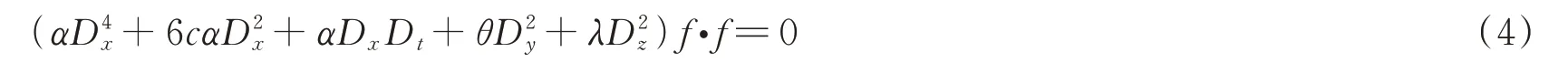
的双线性方程。其中f是关于x，y，z，t的待定函数。满足D-算子。D-算子的定义为

引入试探函数

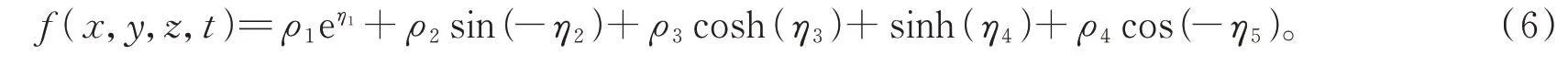
其中ηi=aix+biy+ciz+dit(i=1，2，3，4，5)，ai，bi，ci，di，ρi(i=1，2，3，4)为待定常数。

将 式（6）代 入 方 程（4）中，并 令eη1，sin(η2)，cos(η2)，cosh(ηi)，sinh(ηi)(i=3，4)，sin(η5)，cos2(η2)的系数为零，即可得到一组非线性代数方程组，利用符号计算系统Mathematica，求出该方程组的如下几种解：

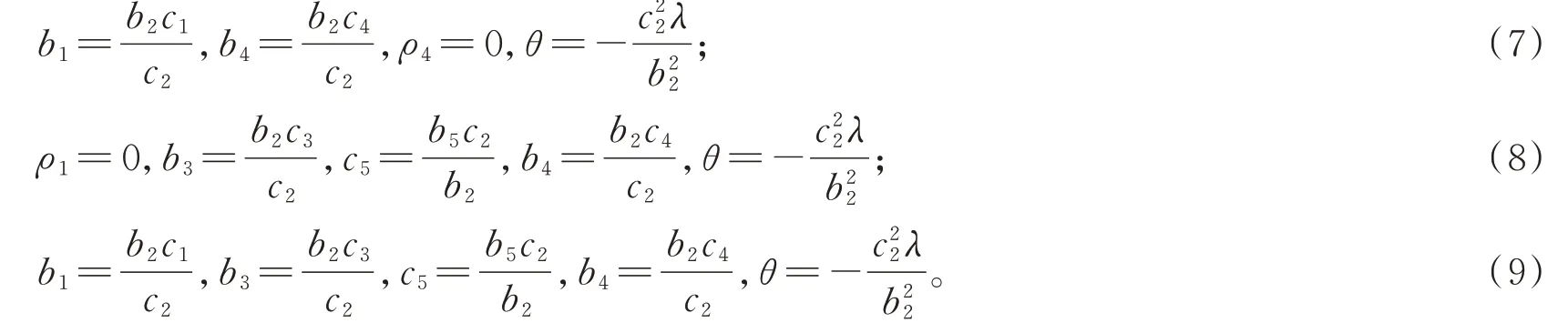
将式（9）代入式（6）得

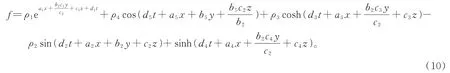
将式（10）代入式（3）得方程（2）的解为

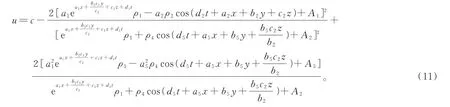
其中

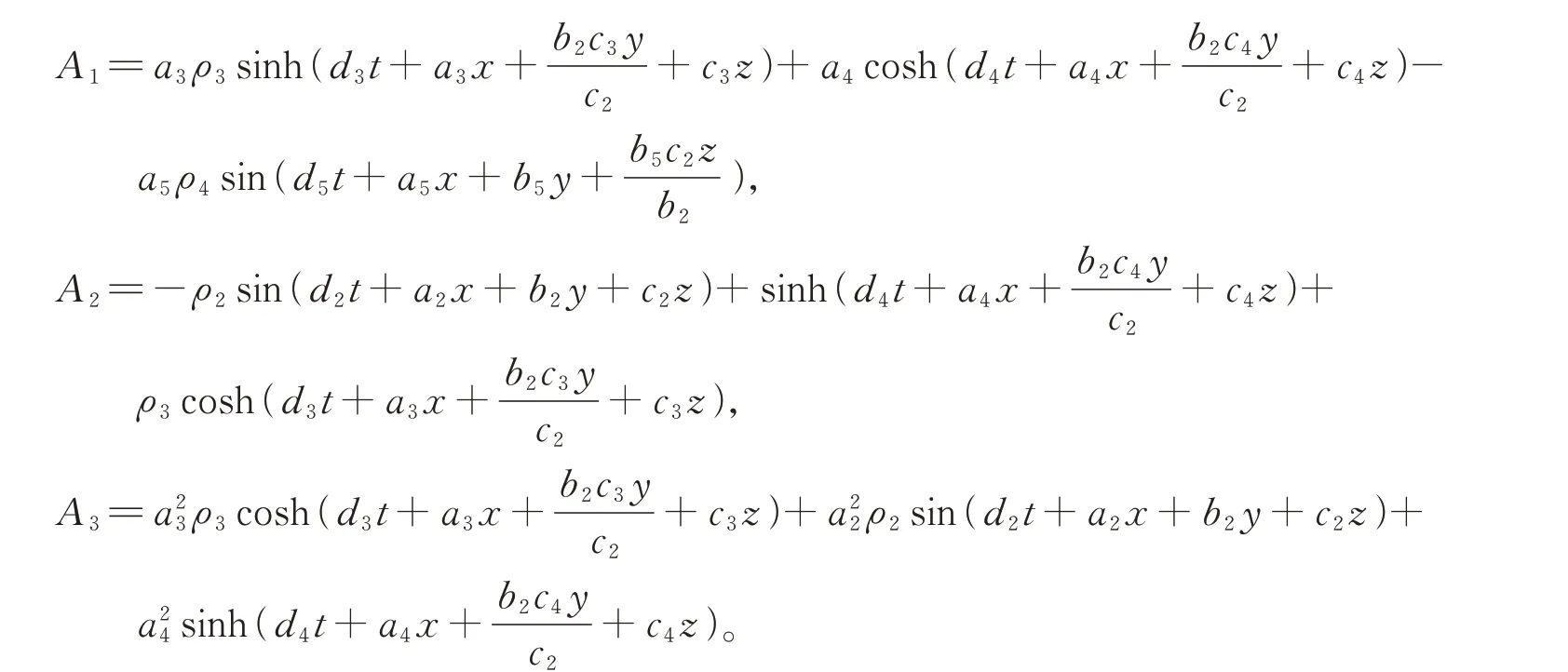
选 取 适 当 参 数c=6，a1=-2，c1=-3，d1=3，c2=1，ρ1=-4，ρ2=-4，ρ3=-3，ρ4=1，d2=-3，b2=7，a2=4，a4=-3，a5=-4，d4=1，c4=2，d5=-3，b5=3，a3=8，c3=1，d3=2，x=0，y=0并代入解（11），得到方程的如下解：

解（12）的特征图如图1所示。

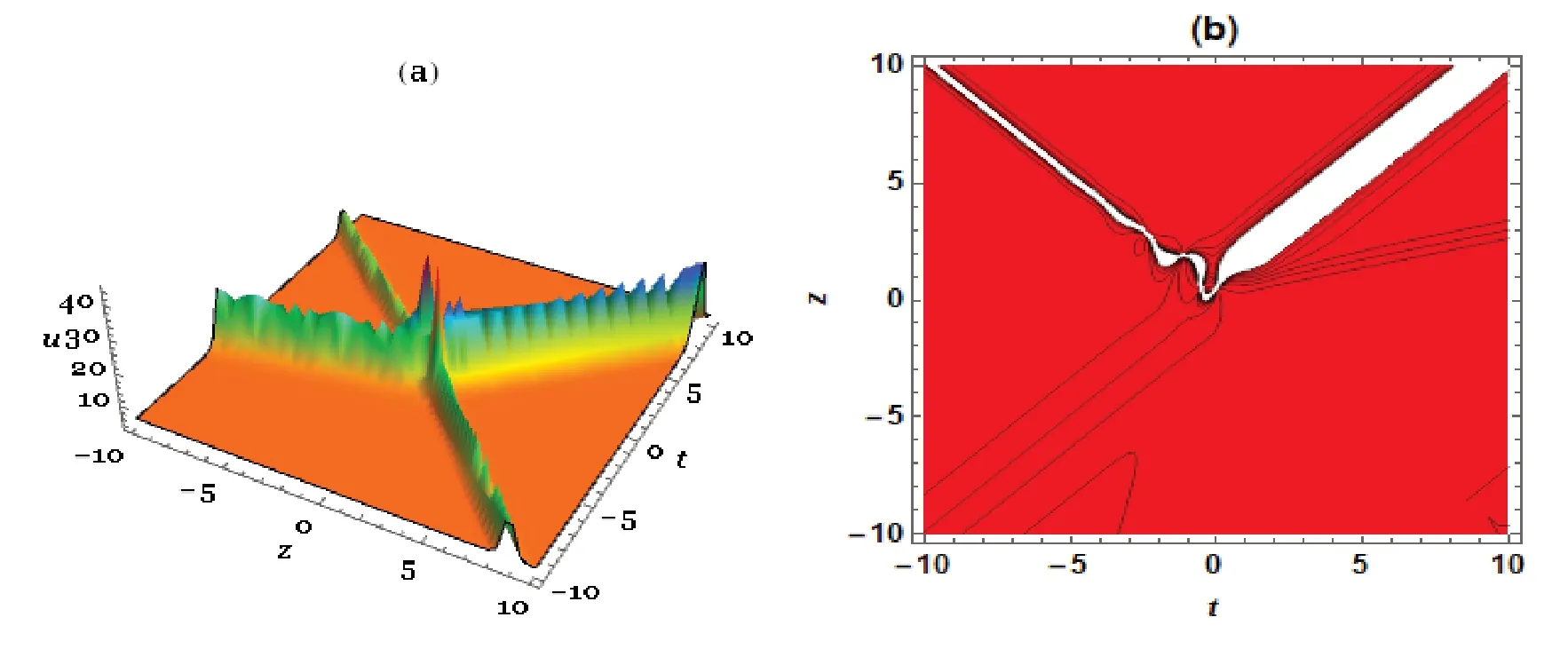
图1 当y=x=0时，u(x，y，z，t)关于z，t的图像Fig.1 When y=x=0，3D plot and contour plot related to z and t corresponding to formula

2 （3+1）维KdV方程的lump新解

引入试探函数

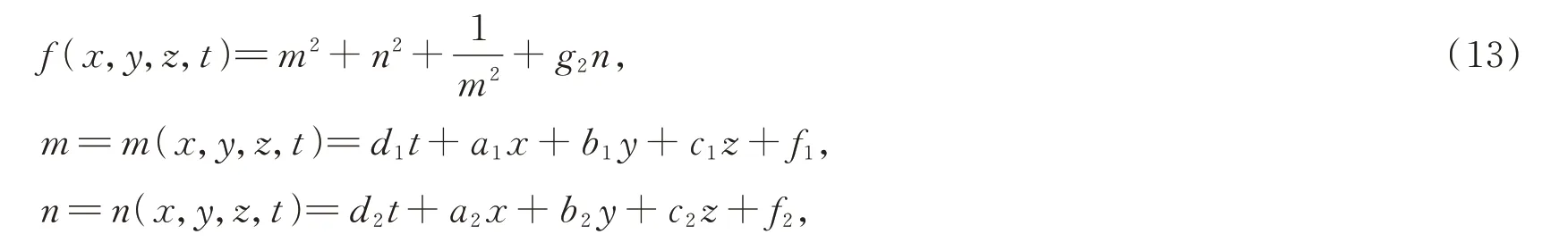
其中ai，bi，ci，di，fi(i=1，2)是待定常数。

将式（13）代入方程（4）中，并令t2，tx，ty，tz，xy，xz，yz，x2，y2，z2，的系数为零，得到一组非线性微分方程组，利用符号计算系统Mathematica得到该方程组的如下几组解：

将式（14）代入式（13）后，并将得到的结果代入式（3）得到方程（2）的解

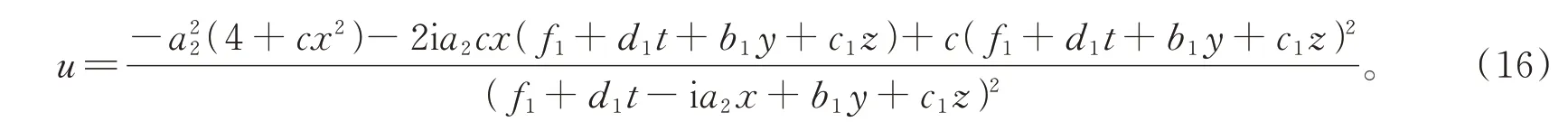
选取适当参数c=1，a2=1，g2=1，f1=1，f2=1，d1=1，c1=2，d2=1，b1=1，x=0，y=0，α=1，β=6，γ=6，θ=1，δ=1，λ=1并代入式（17）化简得到方程（2）的解

解（17）的特征图如图2所示。

图2 当c=1，a2=1，g2=1，y=x=0时，u(x，y，z，t)关于z，t的图像Fig.2 When c=1，a2=1，g2=1，y=x=0，3D plot and contour plot related to z and t corresponding to formula

3 （3+1）维KdV方程的exp-ln-分式新解

引入试探函数

其中φi=aix+biy+ciz+dit，ai，bi，ci，di(i=1，2，3)为待定常数。

将式（18）代入方程（4），令eφ1，的系数为零得到一组非线性方程组，利用符号计算系统Mathematica得到该方程组的解

将式（19）代入式（18）得

将式（21）代入式（3）得到方程（2）的解

其中

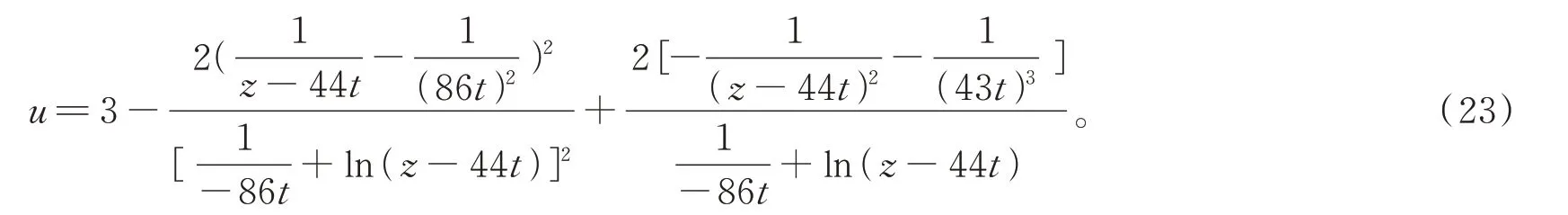
解（23）的特征图如图3所示。

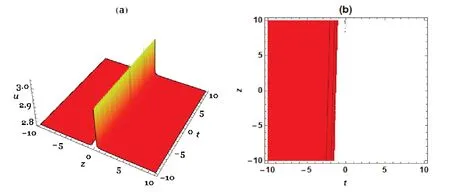
图3 当y=x=0时，u(x，y，z，t)关于z，t的图像Fig.3 When y=x=0，3D plot and contour plot related to z and t corresponding to formula

4 （3+1）维KdV方程的新分式解

引入试探函数

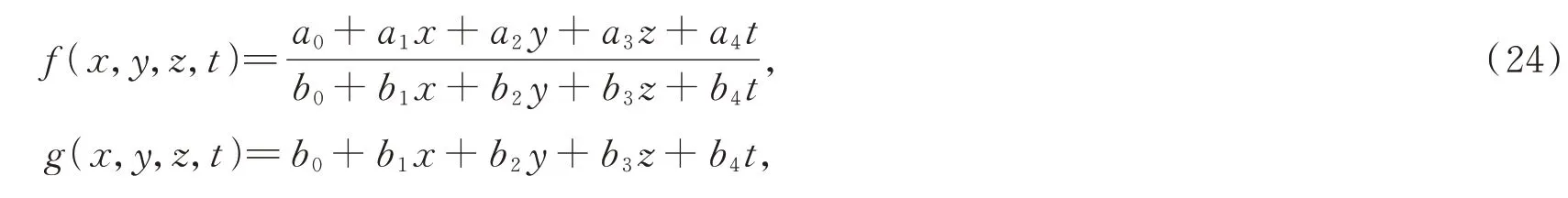
其中ai，bi(i=0，1，2，3，4)是待定常数。

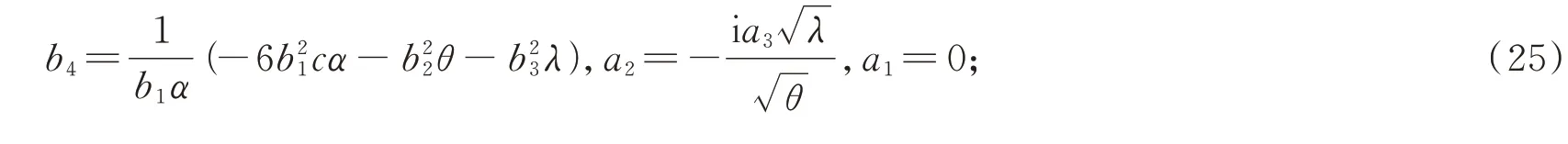
将（27）代入式（24）后，代入式（3）得到方程（2）的解为

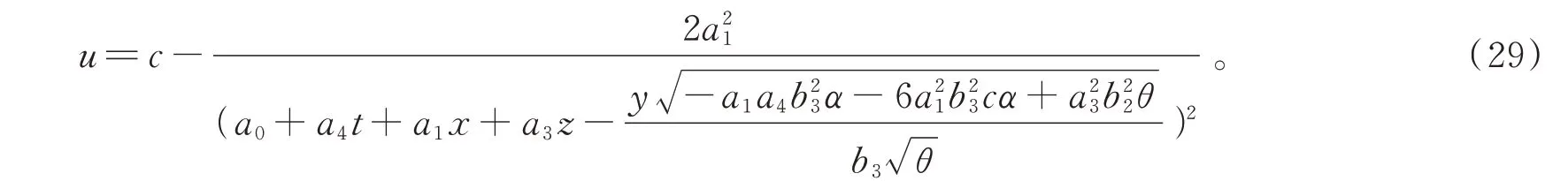
选 取 适 当 参 数a0=1，a1=1，a3=2，a4=1，x=0，y=0，c=1，b3=2，α=1，β=6，γ=6，θ=1，δ=1，λ=1并代入式（31）得到方程解

解（30）的特征图如图4所示。

图4 当a0=1，a1=1，a3=2，y=x=0时，u(x，y，z，t)关于z，t的图像Fig.4 when a0=1，a1=1，a3=2，y=x=0，3D plot and contour plot related to z and t corresponding to formula

5 （3+1）维KdV方程的exp-tanh新解

引入试探函数

其中φi=aix+biy+ciz+dit(i=1，2)，ai，bi，ci，di，ξi(i=1，2，3)为待定常数。

将式（31）代入方程（4）中，令eφ1sech2(φ2)，e-φ1sech2(φ2)，eφ1tanh(φ2)，e-φ1tanh(φ2)，的系数为零得到一组非线性方程组，通过符号计算系统Mathematica得到该方程组的以下几组解：

将式（33）代入式（31）得

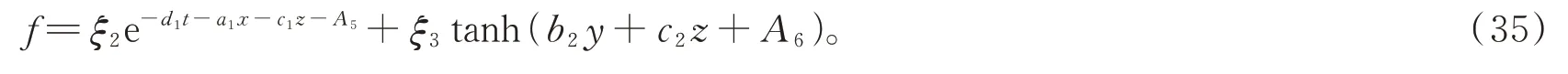
将式（35）代入式（3）得到方程（2）的如下解：

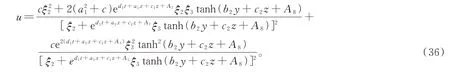
选 取 适 当 参 数c=-1，ξ2=1，ξ3=1，a1=1，b2=1，c1=1，c2=1，d1=2，α=1，β=6，γ=6，θ=1，δ=1，λ=1并代入（36）式得到方程如下解：

解（37）的特征图如图5所示。

图5 当c=-1，ξ2=1，ξ3=1，y=x=0时，u(x，y，z，t)关于z，t的图像Fig.5 When c=-1，ξ2=1，ξ3=1，y=x=0，3D plot and contour plot related to z and t corresponding to formula

6 （3+1）维KdV方程的有理新解

引入试探函数

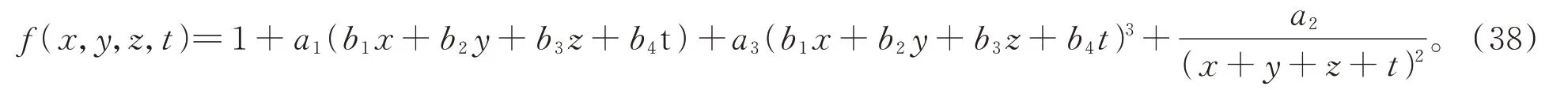
其中ai，bj(i=1，2，3；j=1，2，3，4)是待定常数。

将式（38）代入方程（4）中，令xi，yi，ti，zi(i=2，3，4)的系数为零得到一组非线性方程组，通过符号计算系统Mathematica算出方程的如下几组解：

将式（40）代入式（38）得

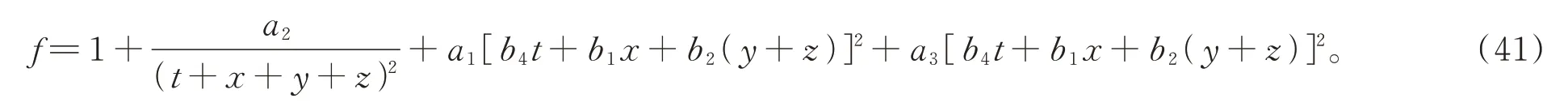
将式（41）代入式（3）中，得到方程（2）的解

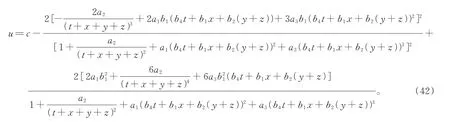
选取适当参数c=-10，a1=-10，a2=1，b2=2，a3=-3，b1=10，b3=1，b4=2，x=0，y=0并代入（42）式得到方程如下解：

解（43）的特征图如图6所示。

7 结论

本文在广田双线性法的基础上，利用试探函数法以及符号计算系统Mathematica，得到了（3+1）维KdV方程新的lump解，以及三角函数、双曲函数、指数函数、对数函数、分式函数基本函数的复合函数新解。

文献［6］中对于广义（2+1）维KdV方程利用变换u=2(lnf)x+c0把方程变为双线性方程，并利用测试函数f(x，y，z，t)=a1cosξ1+a2sinξ2+exp(-ξ3)+a3expξ3，其中ξi=kix+hiy+wit(i=1，2，3)，得到了方程的周期孤波解。本文在其基础上得到了（3+1）维KdV方程的包含正余弦函数、双曲正余弦以及指数函数的周期解。

文献［7］通过Hirota变换把类9阶KdV方程化为双线性形式，引入多项式试探函数，得到5族有理解。文献［8］通过Hirota变换将（3+1）维KdV方程化为双线性方程，并定义了一种符号函数，代入方程得到实值型怪波解。本文在上述两篇文献基础上加以改进，得到了（3+1）维KdV方程新的有理解。

图6 当c=-10，a1=-10，a2=1，y=x=0时，u(x，y，z，t)关于z，t的图像Fig.6 When c=-10，a1=-10，a2=1，y=x=0，3D plot and contour plot related to z and t corresponding to formula