非连续Kummer边值问题解的相似构造法

卫林芳，王桂霞，2，陈德财

（1.内蒙古师范大学 数学科学学院，内蒙古 呼和浩特 010022；2.内蒙古自治区应用数学中心，内蒙古 呼和浩特 010022）

Hermite多项式和Laguerre多项式是量子物理学中两个非常重要的特殊函数，在量子力学和量子光学中有实质的应用［1-8］。例如Hermite多项式可以描述量子谐振子本征态的波函数，也是分数阶Fourier变换的本征函数。Laguerre多项式与氢原子、类氢原子和碱金属原子体系的能级和径向波函数有关，氢原子薛定谔方程解的径向部分是Laguerre多项式。而Hermite多项式Hn及Laguerre多项式Ln都可以用Kummer函数F(α，γ，x)表示，即

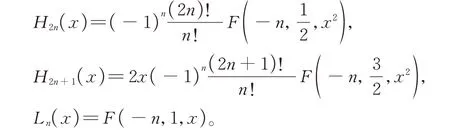
上述Kummer函数是Kummer方程的解。因此，对Kummer方程求解方法的研究具有一定的理论意义和应用价值。

2006年，李顺初研究了Bessel方程边值问题

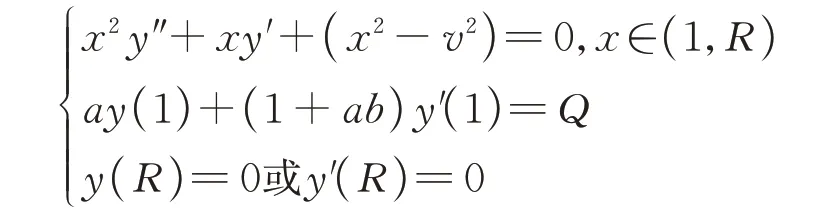
的解式，其中a，b，v，Q，R均为实常数且R＞1。证明了其解具有与连分式相对应的相似性［9］，将数、形、式三者有机结合。其后，该方法被应用到Thomson方程、第一种 Weber方程、一类Airy方程的边值问题、Euler微分方程、Kummer方程等超几何微分方程边值问题及一些油气藏工程中的渗流方程边值问题解式的研究中［10-14］。

由于非连续常微分方程边值问题在力学、地球物理及工程问题中的广泛应用，2015年，文献［15］研究了复合型合流超比方程边值问题的解式

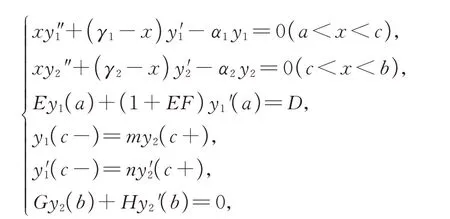
在此基础上，本文研究了带一般转移条件的非连续Kummer方程边值问题

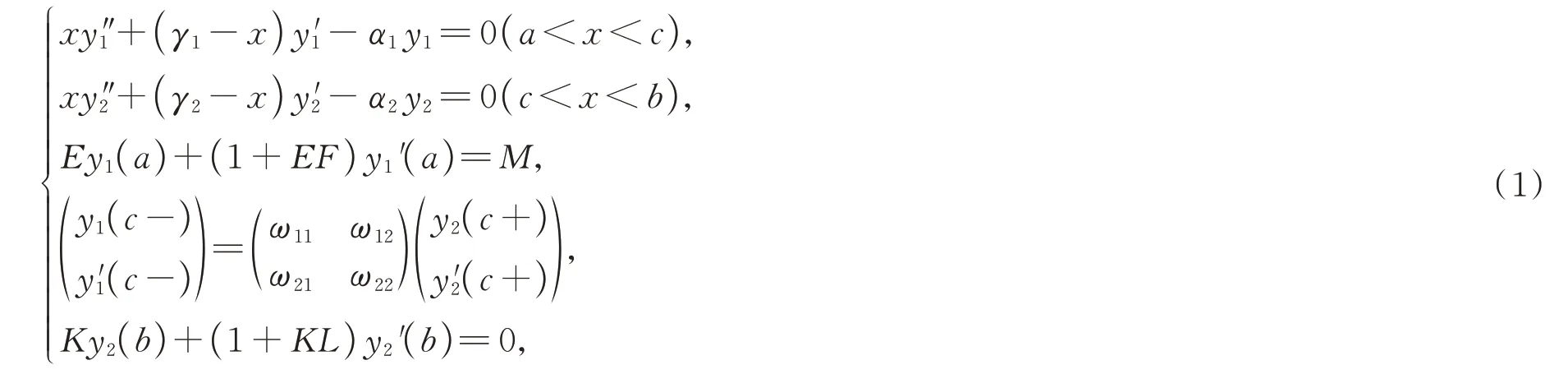
其中K，L，E，F，a，b，c，ω11，ω12，ω21，ω22为已知的实常数，α1，α2，γ1，γ2为谱参数且0＜a＜c＜b，M≠0。该问题可以退化为文献［15］中的边值问题，研究工作更具一般性。

1 预备知识

引理1［16］标准的Kummer方程

的通解可以为

其中A，B为任意常数，γ≠整数，

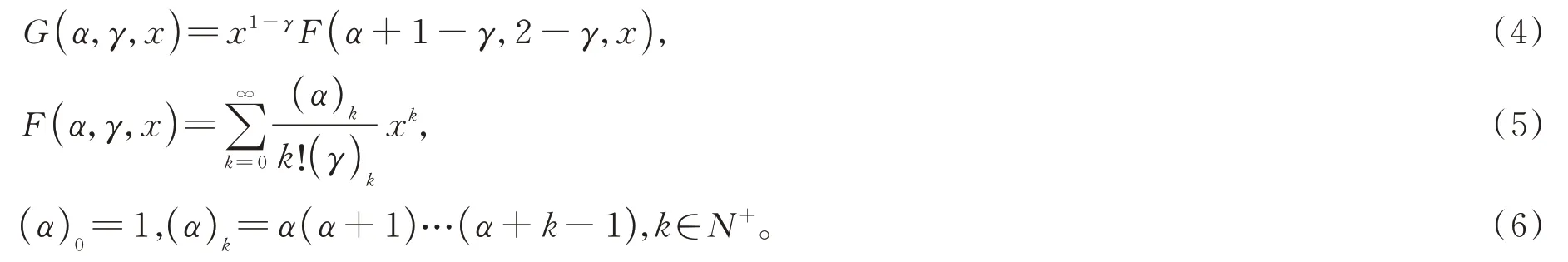
注形如式（5）的Kummer函数F(α，γ，x)为第一类Kummer函数。

引理2［16］若F(α，γ，x)是第一类Kummer函数，则

证明 由式（7）可得

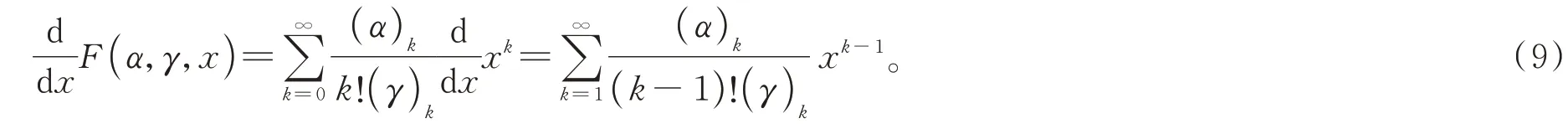
令m=k-1，则式（9）可改写为

由式（10）和式（4）可得式（8）。

引理3若构造二元函数

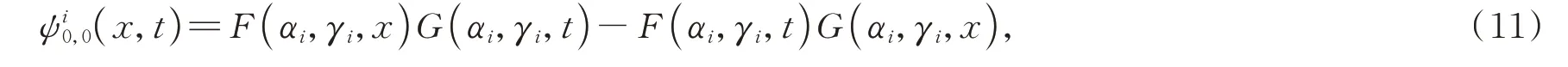
则

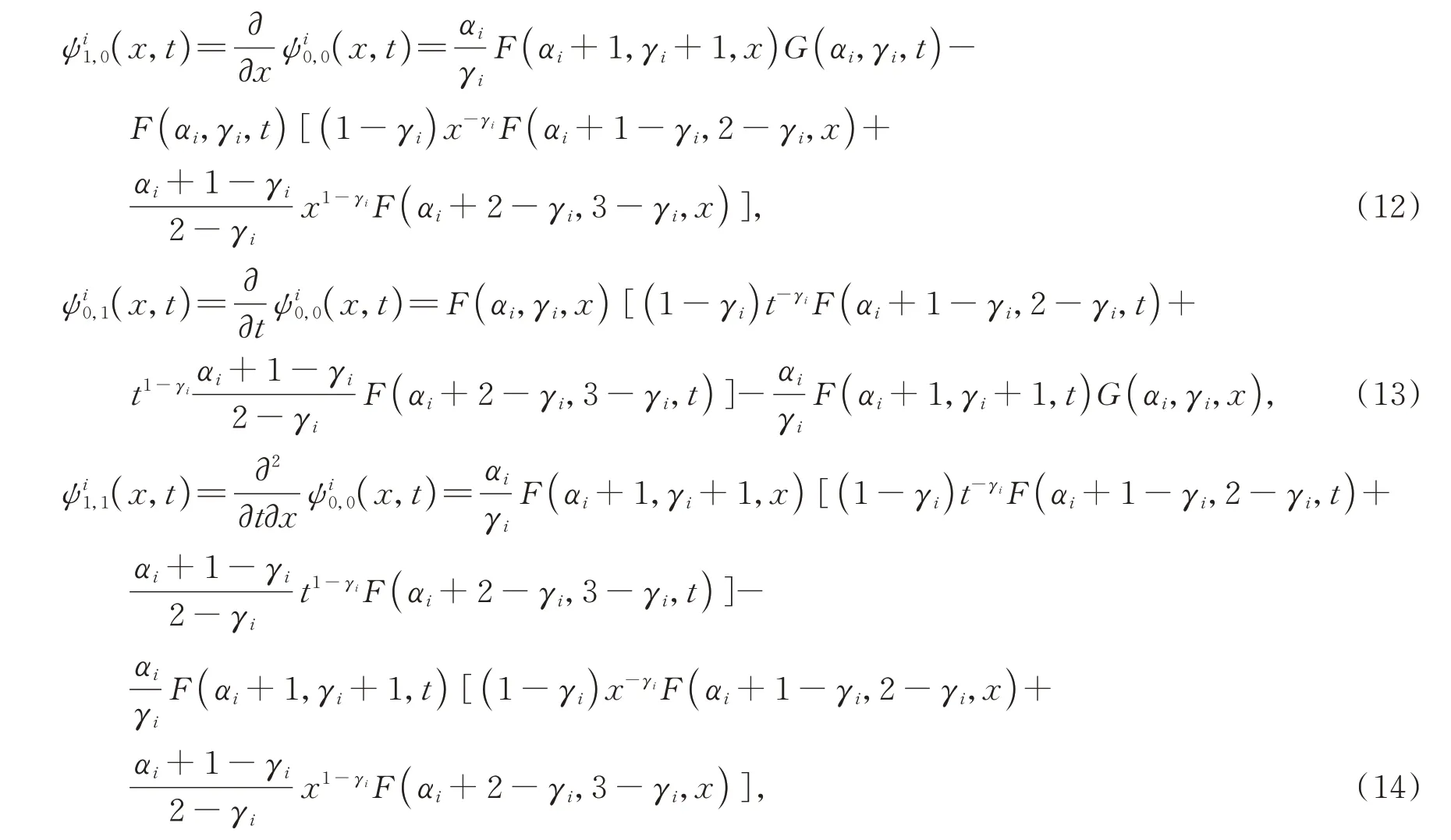
其中：i=1代表左区间a＜x＜c；i=2代表右区间c＜x＜b。

证明结合引理2，经简单计算可得。

2 定理及其证明

定理1若边值问题（1）有解，则其解为

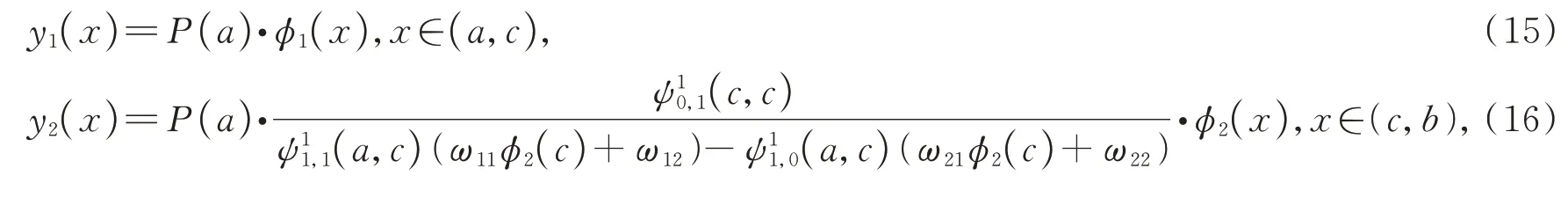
其中

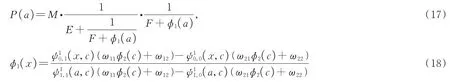
称为边值问题（1）在区间(a，c)的相似核函数，

称为边值问题（1）在区间(c，b)的相似核函数。

证明由引理1知，若定解方程的通解格式

则

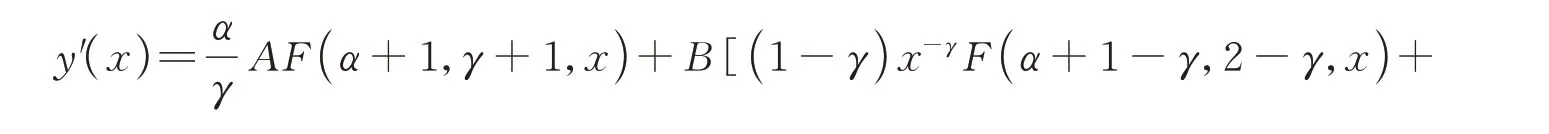
结合式（20）和边值问题（1）中的边界条件得

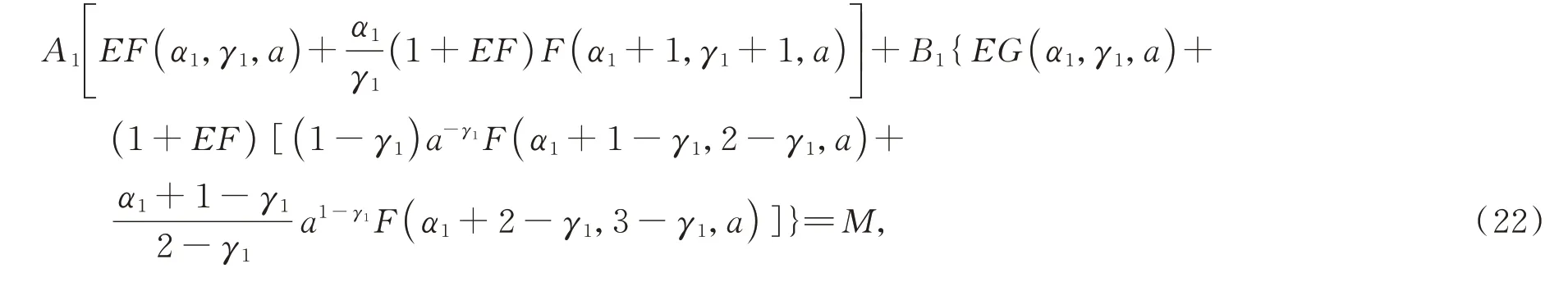
式（20）结合边值问题（1）中的转移条件得

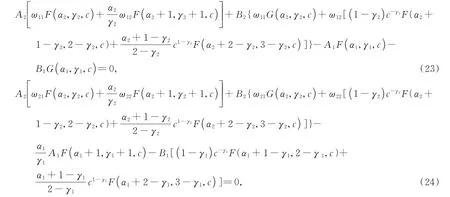
式（20）结合边值问题（1）中的右边界条件得

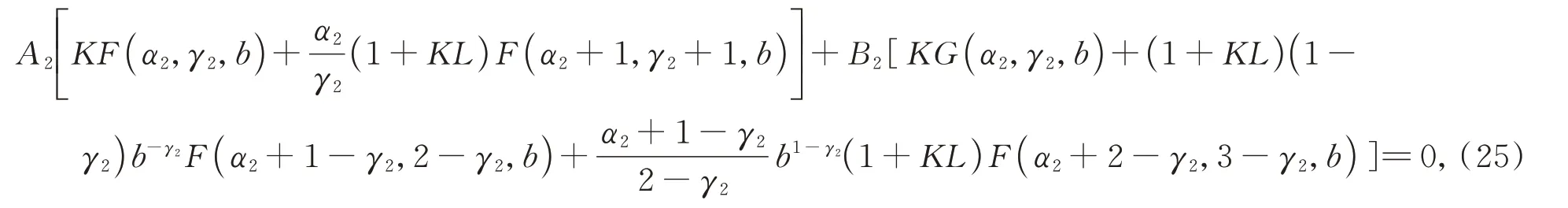
由式（22）-（25）求得

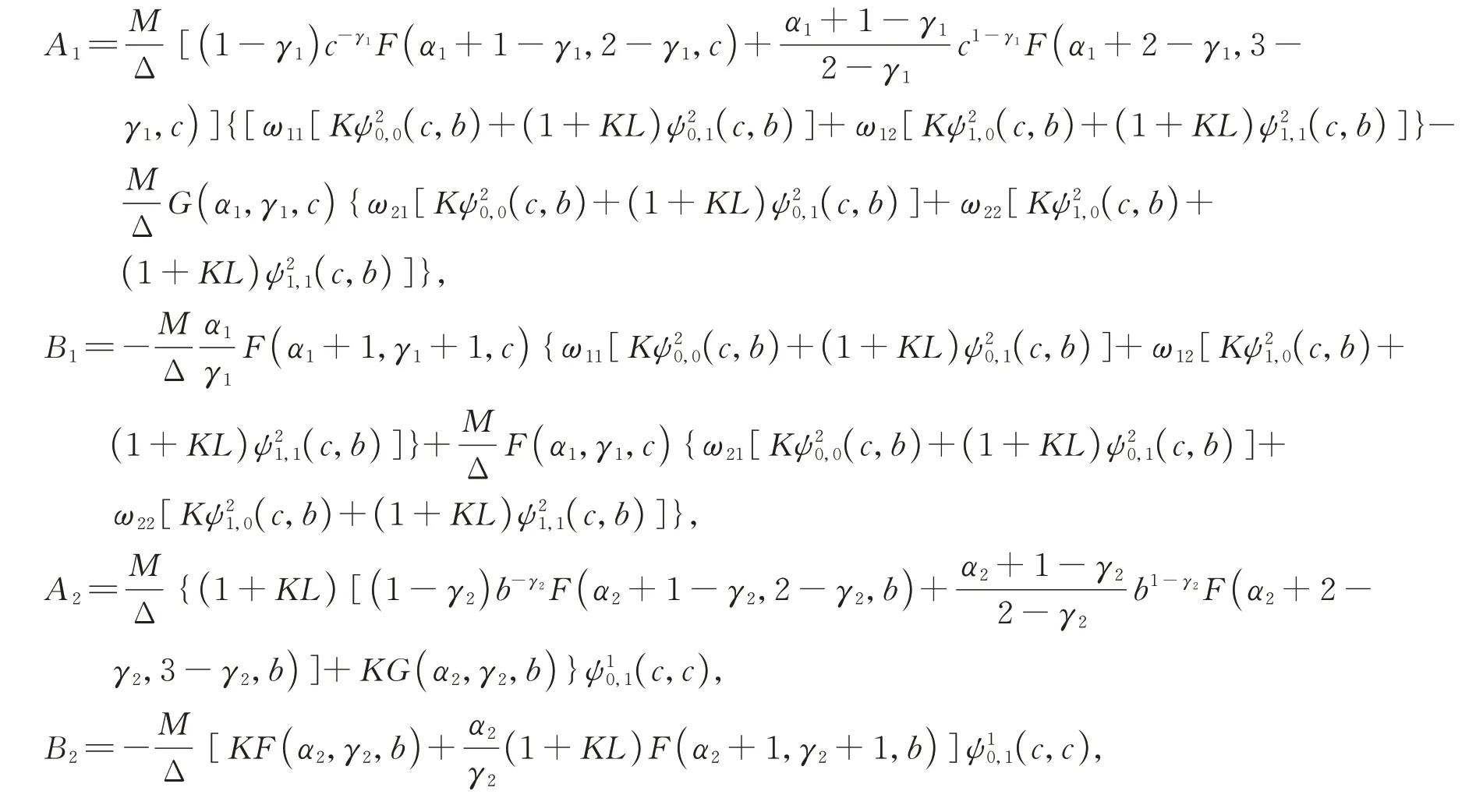
其中

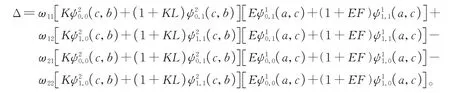
由此可得到边值问题（1）在区间(a，c)的解

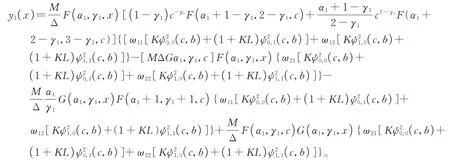
简记

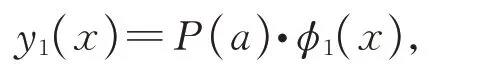
其中

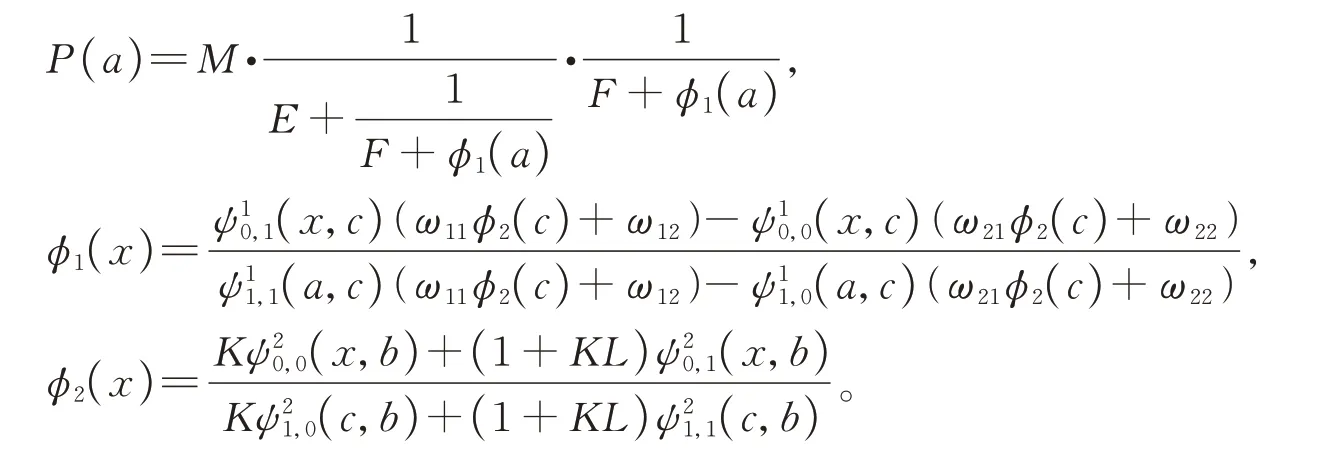
同理

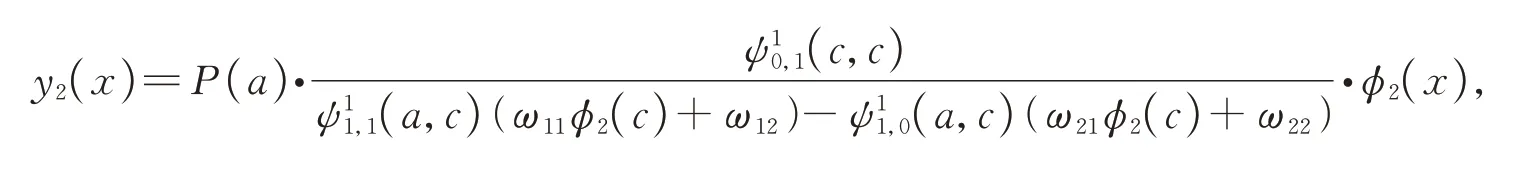
其中

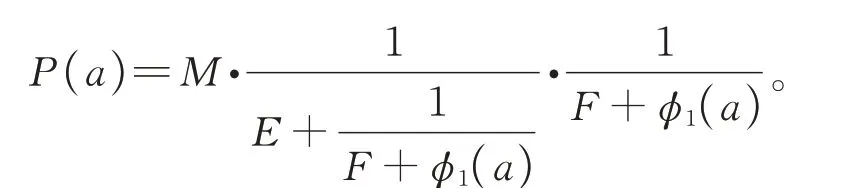
3 实例

给定非连续Kummer方程边值问题

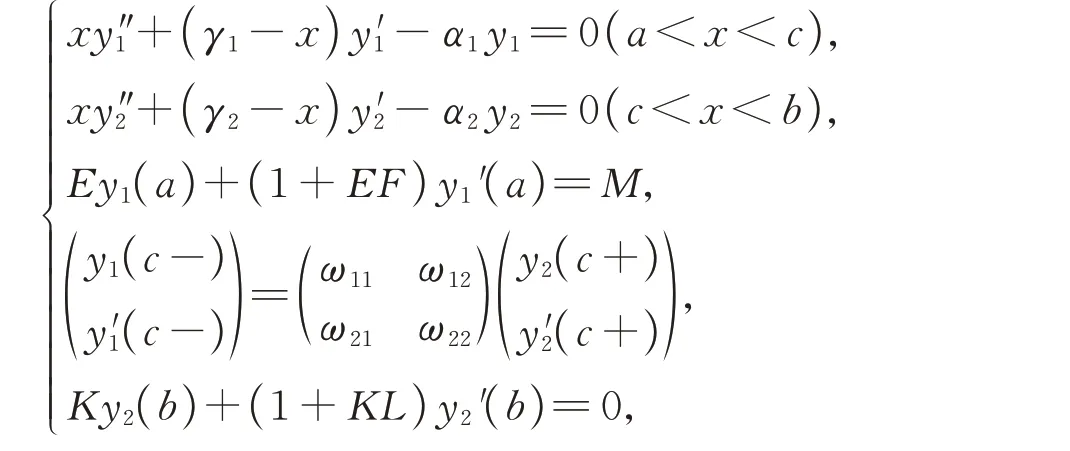
取a=1，b=3，c=2，α1=α2=1，γ1=0.5，γ2=-0.5，K=E=M=1，F=L=0，ω11=ω22=1，ω12=ω21=2。

由式（15）和式（16）所得问题的解如图1所示。经验证，该结果与解析解的结果一致。图2展示了解对边界条件的依赖性。

由图2（a）和（b）可知，若其他参数不变，对于固定的自变量x，当边界条件中的非齐次项M增加时，函数值与导数值均增加。由图2（c）和（d）可知，若其他参数不变，对于固定的自变量x，当边界条件中的系数E增加时，函数值与导数值均减小。

4 小结

图1 解y1与y2Fig.1 The solution of y1 and y2

本文通过Kummer方程的两个线性无关解构造了相似核函数，并根据边值问题解的相似构造理论，研究了带一般转移条件的非连续Kummer方程边值问题的解式，数值实例验证了该方法的有效性，结果图展示了解对边界条件的依赖性。相似构造法得到的解式适用于一类问题，该方法避免了同类问题的重复求解，提高了求解效率，有一定的实际意义，同时，通过解式可以直接观察解与边界条件和转移条件的关系。

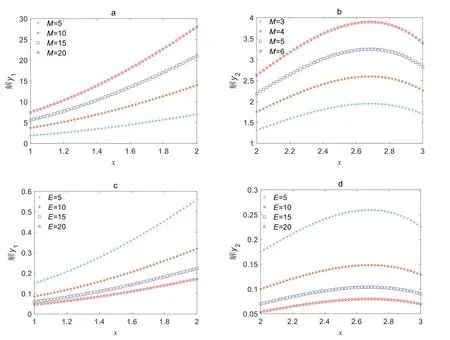
图2 y1及y2对M和E的依赖性Fig.2 Dependence of y1 and y2 on M and E