修正Boussinesq方程的N-次Darboux变换与精确解

乌日乐，套格图桑，2，扎其劳，2

（1.内蒙古师范大学 数学科学学院，内蒙古 呼和浩特 010022；2.内蒙古自治区应用数学中心，内蒙古 呼和浩特 010022）

1872年，法国力学家，理论物理学家，M.J.Boussinesq在浅水波的研究中导出一个含有孤立子解的非线性方程，后来人们称之为Boussinesq方程［1］。该方程和KdV方程都是描述浅水波运动的基础模型，且它包含双向传播的孤立子。

众所周知，Miura变换将KdV方程与修正KdV方程联系起来。类似，Boussinesq方程也存在其修正模型，即修正Boussinesq方程［2］

它具有Hamilton结构［2］

著名Boussinesq方程

可写成

文献［2］中给出Boussinesq 方程（3）与修正Boussinesq方程（1）之间进行如下Miura变换

修正Boussinesq方程（1）具有3×3矩阵Lax对

其中Ri(i=1，2，3，…，8)是李代数sl(3，R)的一组基［2］

利用相容性条件Φxt=Φtx可得方程（1）。

在文献［3］中，基于显式约束和高阶约束下给出方程（1）的两种分解。相应的Lax方程组被非线性化，且得到有限维可积Hamilton系统。在文献［4］中，建立方程（1）的具有多参数的Darboux变换，且变换中需要满足两组约束条件。文献［5］给出修正Boussinessq方程（1）的一种简单的没有约束条件的 Darboux 变换和该方程的无穷多守恒律。

本文首先给出修正Boussinessq方程（1）的N-次Darboux变换及其证明，然后分别利用Darboux变换和Miuta变换（6）-（7）获得修正Boussinessq方程（1）和著名Boussinesq方程（3）的一些精确解。

1 Darboux变换

把Lax对（8）-（9）改写成

其中

如果线性变换

称为修正Boussinessq方程（1）的Darboux变换，则非退化的矩阵T把Lax对（10）-（11）变成为新Lax对

命题1如果y和x是方程（1）的解，则式（12）中的T是（8）式的Darboux矩阵， 它将(y，z)和分别变为同一个方程（1）的解。

即

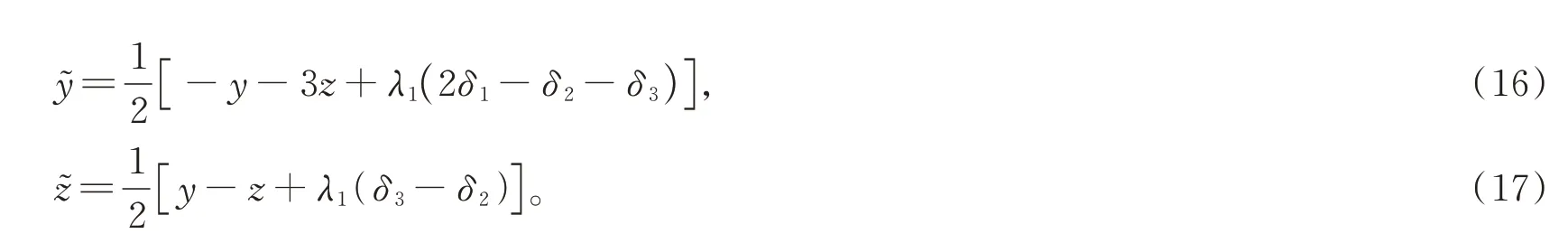
证明将式（15）和代入式（13）的第二个表达式， 得

收集式（18）中λ各次幂的系数，并令其为零得

式（19）自然满足。由式（16）-（17），已知式（20）成立。由式（21），得

此时，命题1得证。

命题2如果y和z是方程（1）的解，则在式（16）-（17）和式（22）-（24）条件下，式（12）中的T是式（9）的Darboux矩阵。

证明把（15）和代入式（14）的第二表达式，得

收集式（25）中λ各次幂的系数，并令其为零得

式（26）显然成立。由式（16）-（17），得式（27）成立。又由式（16）-（17）和式（22）-（24），得式（28）成立。再由式（16）-（17）和式（22）-（24），化简式（29）得

此时，命题2得证。

取 方 程（1）的 种 子 解 为(y0，z0)，当λ=λk(k=1，2，…，N)时，计 算 出Lax对（10）-（11）的 为依据命题1-2，通过重复使用Darboux变换可迭N-次Darboux 变换。

一次Darboux变换

二次Darboux变换

其中

这里δ1，δ2，δ3在式（33）中给出。

N-次Darboux变换

其中

2 精确解及其分析

根据命题1与命题2，取y=z=0为方程（1）的种子解， 将种子解代入Lax对（10）-（11），可计算出Lax对的一组基本解：

当k=1时，将式（44）-（46）中的(f1(1)，f2(1)，f3(1))T和种子解y0=0，z0=0代入一次Darboux变换（31）-（32），得修正 Boussinesq方程（1）的一个精确解

其 中(f1(1)，f2(1)，f3(1))T在 式（44）-（46）(k=1)中 给 出。当 参 数 取时，得修正Boussinesq方程（1）的精确解。 图1 展示了该解的性质。

图1 修正 Boussinesq 方程（1）的精确解Fig.1 The exact solution of modified Boussinesq equation （1）

把式（47）-（48）代入Miura变换（6），得著名Boussinesq方程（3）的一个精确解

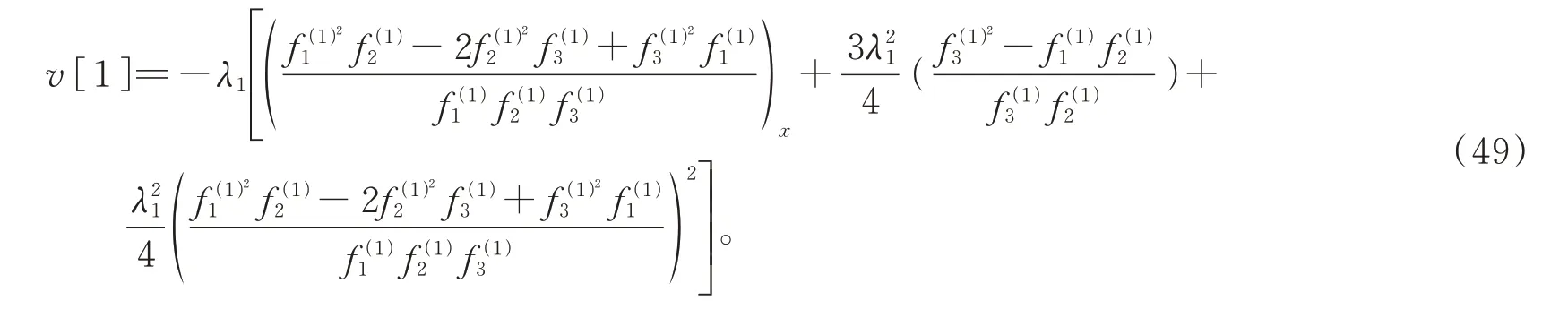
当k=1，2时，将式（44）-（46）中的(f1(k)，f2(k)，f3(k))T和种子解y[1]和z[1]代入二次Darboux变换（34）-（35），得修正Boussinesq方程（1）的另一个精确解。重复上述过程，利用N-次Darboux变换，可得修正Boussinesq方程的更多精确解。还可以利用Miura变换（6）， 得著名Boussinesq方程（3）的更多精确解。

3 结论

文献［4］给出方程（1）的 Darboux变换，其中含有两个关系式作为附加条件，而本文给出的N-次Darboux变换形式简单，无附加条件。此外，本文利用Boussinesq方程和修正Boussinesq方程之间的Miura变换，获得Boussinesq方程的孤子解。Darboux变换是求解孤子方程的一种有效方法［7］。该方法被广泛地应用于孤立子与可积系统理论中。本文中的Darboux变换是使用普适的，纯代数的算法构作而成。通过Darboux变换的迭代，可以获得修正Boussinesq方程（1）和Boussinesq方程（3）的一系列精确解。

图2 著名 Boussinesq 方程（3）的孤立子解Fig.2 The soliton solution of modified Boussinesq equation （3）