谢洪赉译著《最新中学教科书代数学》初探

徐世宜，郭金海

（1.中国科学院 自然科学史研究所，北京 100190；2.中国科学院大学，北京 100049）

清朝最后的十余年，中国出现编译教科书的热潮，涌现出大量中学数学教科书。这些中学数学教科书多译自日本，但也有一些译自欧美，清末翻译家谢洪赉翻译的《最新中学教科书代数学》［1］属于后者。该书译自美国米尔恩（William James Milne，1842—1914）编写的《中学代数学》（High School Algebra），1905年由商务印书馆出版。它是“癸卯学制”颁行后国人编译的中学代数教科书中较早的一部。系统研究该书的底本、翻译情况、流传和影响，可以了解美国中学教科书在晚清的传播情况以及谢洪赉的贡献，并揭示中学数学教科书编译过渡时期的特征。

关于《最新中学教科书代数学》，魏庚人［2］和代钦［3］等学者做过习题、编排和数学符号等方面的探讨，但学界对该书的底本、翻译背景和翻译情况、流传与影响还未有系统的研究。对于晚清后期的数学教科书，学界多关注译自日本的教科书，对译自美国的教科书关注较少。鉴于此，本文考察该书的底本，论述谢洪赉的翻译背景，探究该书的翻译情况、流传与影响。

1 《最新中学教科书代数学》的底本及其作者

1.1 底本作者米尔恩

米尔恩①谢洪赉将他译作宓尔，现按照《世界人名翻译大辞典》，译为米尔恩。出生于苏格兰，1852年移民美国，1868年毕业于罗切斯特大学（University of Rochester），获文学学士学位，1871和1877年被该校授予文学硕士和哲学博士学位，1878年又被德堡大学（DePauw University）授予法学博士学位，具有良好的知识素养［4］。

米尔恩一生从事教育工作。1863年，他在布罗克波特学院（Brockport Collegiate Institution）开始执教生涯，担任数学和古典学助教［5］，之后先后在罗切斯特学院（Rochester Collegiate Institute）和布罗克波特师范学校（Brockport State Normal School）教授古代语言。1871年，米尔恩担任杰纳西奥师范与培训学校（Geneseo Normal and Training School）首任校长②关于米尔恩担任奥尔巴尼师范学校校长前的经历，见于纽约州教育理事会第104次年度报告。104th Annual Report of the Regents ［R］.Albany： James B.Lyon， 1892： 1543.。1889-1914年，米尔恩担任奥尔巴尼师范学校（State Normal School at Albany）校长，这期间，该校从培养初等学校教师的师范学校升格成培养中等学校教师的师范学院。这是美国第一所升格而成的师范学院，是美国师范教育史上的一个里程碑，米尔恩作为校长，功不可没［6］。米尔恩在教育领域的耕耘为他赢得了良好的声誉，甚至在他年轻时，就被誉为“一位生活毫无污点、具有伟大的人格力量、专注于职业的绅士，全州最成功的教育者之一”［7］。

米尔恩是一位高产的数学教科书作者，一生编写了25卷数学教科书，科目包括算术、代数和几何。这些教科书在美国具有较大的影响。他编写的第一本代数教科书《归纳法代数》（The Inductive Algebra）出版当年就有19所纽约州的学校选用，他的算术教科书也被多所学校选用①数据来源于1893年纽约州大学对各文实学校所使用的教科书的统计，详见纽约州教育理事会第106次年度报告。106th Annual Report of the Regents［R］.Albany： James B.Lyon， State Printer， 1893： 1241.。良好的知识素养、丰富的教育和编书经历以及教科书优秀的反馈，为其教科书的质量提供了保障。

1.2 底本《中学代数学》的内容和特点

《最新中学教科书代数学》的底本是米尔恩于1892年出版的《中学代数学》［8］。该书由《归纳法代数》修订而来，共22章，包括代数基本概念、代数式的加法、减法、乘法、除法、因式分解、公因数、公倍数、分数、一次方程、一次方程组、乘方、开方、无理数的运算、无理方程、二次方程、比率、比例、数列、虚数、对数和二项式定理。此外，该书还介绍了不等式和不定方程的求解、排列组合、级数和方程论等知识，内容比较丰富。

《中学代数学》的突出特点是使用归纳法编写，此外还有内容贴合考试大纲、习题量大等。

1.2.1 使用归纳法编写 归纳法（inductive method）是一种教学方法。美国教育家麦克维卡（Malcolm MacVicar，1829—1904）认为，归纳法包括观察、比较与分类、推论、验证四个步骤［9］。归纳法在美国数学教科书编写中的应用始于19世纪20年代，是美国裴斯泰洛齐运动的产物［10］。用归纳法编写的教科书，一般先给出例题让学生观察、比较与分类，再由例子总结出法则，最后用练习来验证和应用，即引入、总结、应用三个环节。

与归纳法相对的是演绎法。用演绎法编写的教科书一般直接给出法则，再用例题加以解释，最后练习巩固。两者相比，归纳法更注重学生的理解过程，贴合学生的学习心理。如米尔恩所说：“通过自然且适当递进的练习，引导学生彻底理解学科的原理。”［8］3这一时期的美国中学代数教科书多用演绎法编写，因而用归纳法编写的《中学代数学》颇具特色。

1.2.2 内容遵循考试大纲 1880年，纽约州教育理事会（Board of Regents）出台了该州首部高等考试（Advanced Examination）大纲，随后又多次修订。米尔恩注重教科书内容与考试大纲的一致，在其1908年出版的《标准代数》（Standard Algebra）的前言中，他明确提到该书的内容范围与“纽约州教育理事会对初等与中等代数课程的要求”相一致［11］。在编写《中学代数学》时，他应参考了1891年版大纲。对比1891年大纲与《中学代数学》，发现两者涉及的知识点基本吻合［12］。1905年，大纲增加了知识点“方程的图象解释”和“虚数和与差的图象表示”［13］，而在次年再版的《中学代数学》中，米尔恩增加了一章“图解代数”（graphic algebra），介绍方程的图解法和虚数的几何表示［14］。其更新之及时，反映了他对大纲的遵循。

1.2.3 习题量大 《中学代数学》包含超过4 000道习题，仅代数式乘法章就有近300道，远超其他教科书。米尔恩不仅在每个知识点后设置习题，还额外设置复习题，以巩固此前所学知识。事实上，习题量大且注重复习，是米尔恩的代数教科书共有的特点。他认为大量的习题有益于学生快速且牢固地掌握知识［8］3，但这也可能使学生陷入重复劳动，从而造成负面影响。

由于《中学代数学》附录的答案没有求解步骤，米尔恩另出了一本答案册，给出了他认为有一定难度的习题的求解步骤［15］。答案册实际上标明了练习的重点，有利于学生自学。

《中学代数学》也有不足。该书部分章节的名称与内容不够匹配，如虚数章包含了不等式和不定方程的知识。此外，该书在论及级数等知识时，表述不严谨［8］336。但瑕不掩瑜，该书仍是一部质量过关、特点突出的教科书，且使用广泛，直至1915年仍有学校选用②北卡罗莱纳州格林斯博罗（Greensboro）的沐恩中学（Immanuel Lutheran College）在1915-1916学年选用《中学代数学》作为教科书。见于该校1915-1916学年的情况一览（Catalogue of Immanuel Lutheran College）。。

2 谢洪赉的译书背景

1895年甲午战败后，以译书促教育得到了清朝朝野上下的广泛认同。光绪皇帝要求“由官设书局编译中外要籍”，以作为中小学的教材［16］；罗振玉也提出“时时取东西各国新出之书，随时译出，逐渐将旧本改良，以资应用”［17］。这一时期，商务印书馆等民间翻译机构兴起，他们的一项重要业务即编译出版外国教科书。

1904年1月“癸卯学制”颁行。这是中国第一个正式颁布并在全国施行的学制，首次将学校教育制度化、系统化，对学校课程做出了较为具体的要求，如中学堂每星期应有4个钟点的数学课，其中第2、3、4年学习代数［18］167-168，170。“癸卯学制”颁行后，学校急需符合学制要求的教科书，但官编教科书难以及时满足需求。因此，在官编教科书出版前，清政府允许民间自编教科书［18］187。于是，民间各出版机构在教科书领域展开了激烈竞争，而商务印书馆为其中的佼佼者。

商务印书馆创办于1897年，于1902年设立编译所专门编写教科书，由蔡元培任所长，不久由张元济接任［19］。编译所自1903年起开始编写系列教科书《最新教科书》，于1904年开始出版。该系列教科书质量很高，在当时众多教科书中脱颖而出，行销甚广。谢洪赉翻译的《最新中学教科书代数学》即为该系列教科书中的一部。

谢洪赉（1873—1916）毕业于苏州博习书院，先后任教于苏州博习书院、上海中西书院。他与商务印书馆关系密切。其妹夫鲍咸恩是商务印书馆的一位创始人，其弟也在商务印书馆工作［20］。谢洪赉“以书籍为教育之利器，著述为开化社会之先驱”［21］21，乐于协助商务印书馆的工作，且翻译经验丰富，曾协助潘慎文（Alvin Pierson Parker，1850-1924）翻译《代形合参》《八线备旨》等书，商务印书馆出版最早的教科书《华英初阶》亦其译作。谢洪赉重视数学的学习。他认为学习数学有三项益处：一是有益于学问，因为数学是其它学科的基础；二是有益于日用，因为数学有广泛的应用；三是有益于心，通过学算可以“祛其浮气、练其精心、资其定法、发其巧思”［22-23］。所以，谢洪赉编译了包括《最新中学教科书代数学》在内的多部商务版数学教科书，并非意外。

3 《最新中学教科书代数学》的翻译情况

《中学代数学》最早被美国传教士带到中国，曾被厦门同文书院选为教科书［24］。1904年，谢洪赉着手翻译《中学代数学》，于1905年1月在商务印书馆出版，定名为《最新中学教科书代数学》。

3.1 内容忠实底本

谢洪赉在翻译《中学代数学》时没有做大的改动，基本忠实于原著。他仅微调了结构和内容，并采用了一些编译策略。

（1）章节的合并与拆分

谢洪赉仅合并和拆分了个别章节，没有打乱原有的知识次序。这些调整包括：将底本公因数章和公倍数章合并为一章，取名为“生倍”，即“公生”与“公倍”的合称；将数列章中的总复习题单独列为一章“总习问”；将二项式定理章分为三章“二项例”“方程之理”和“总习问”，使与二项式定理无关的方程论部分单独成章。总的来看，谢洪赉对章节的合并和拆分是比较合理的。

（2）内容的微调

谢洪赉自称“参酌我国情形，略为修饰，以合中学程度”，但实际没有删改任何一个知识点。目前仅发现两处与底本不同之处，见表1。

知识点445中，因为四次以上方程没有公式解，所以底本使用了“不可能”（impossible），而译本使用了“最难”。“最难”不是“不能”，此处的翻译也不准确。

表1 《中学代数学》与《最新中学教科书代数学》不同之处Tab.1 Difference between English version and Chinese version of High School Algebra

（3）编译策略的采用

为增加教科书的可读性，谢洪赉采取了一些编译策略。首先是人名和度量衡的本土化，如将“John”改为“小子”，“bushel”改为“斗”。他在译例中称“以哩代英里”，但正文中并未使用“哩”，而是直接改为“里”。

对于读者可能存在疑惑之处，谢洪赉在正文旁添加一行小字，以解释说明。如底本在给出“商”的定义之前，例题中就有“商”字。为避免读者有疑惑，谢洪赉在该例题旁插入提示语：“商者，尤数学之得数也”，使读者对“商”有一个简单的认识［1］上册93。提示语在书中出现的次数不多，但反映出谢洪赉编译工作的细致，体现出他对该书的用心。

谢洪赉在书末附上“代数学中西名目表”，共四页，按英文字母顺序列出了书中数学名词的中、英文名。由于该书中出现的一些名词术语并不多见，中英对照表对于学生辨识名词概念是有帮助的。

3.2 译例的内容

谢洪赉在《最新中学教科书代数学》开篇处写有一篇译例，介绍该书的特点和优点，共六小节。

第一节说明了该书的底本和底本作者“是书以美国纽约师范学校校长宓尔君所著归纳法代数学为原本”［1］译例。谢洪赉所说的“归纳法代数学”不是《归纳法代数》，只是说明底本是用归纳法编写的。对比《归纳法代数》和《最新中学教科书代数学》的内容，发现两者差异较大。谢洪赉还提到：“宓君著算学教科书甚富，即代数教科书亦三种，此为中学所用。”这说明他知道米尔恩还有为初等学校编写的代数教科书。米尔恩的初等学校代数教科书也用归纳法编写，且内容与《代数备旨》相近，并不浅易，但谢洪赉仍选择难度较大的《中学代数学》为底本，可见他对学生的高要求。

第二节介绍了归纳法，谢洪赉首先指出归纳法和演绎法的区别：

授科学之法，有二大别：曰演绎法，先定名目、立界说，而后剖解其理由；曰归纳法，先以浅近之理，罕譬曲引，使学者有所领会，而后定名立说。［1］译例

这段话指出了两种教学方法的形式特点：演绎法直接给出定义，再作解释；归纳法有引入环节，先熟悉知识，再给出定义。谢洪赉用“罕譬曲引”来描写归纳法的引入环节。“罕譬”指教学语言简洁明了，少用难懂的比喻，“曲引”则强调避免直接将知识告诉学生。他对归纳法的形式特点和对引入环节的认识基本正确。

谢洪赉认为，用归纳法编写代数教科书，既能衔接算术和代数的学习，也能让各章之间相互衔接，使学生的学习循序渐进。他还提到，“西国学校算学教科书近年改良颇多，此特其一种，今亟译之以资之学界”［1］译例，指出其翻译目的是向国内介绍用归纳法编写的教科书。这反映了他对改良数学教科书的支持。

第三节介绍了米尔恩对底本优点的自述，包括章节安排循序渐进，言语简洁、定义明晰，推理过程清楚得当，能使学生对知识记忆深刻。该节内容来源于《中学代数学》的前言，谢洪赉只略作修饰。

第四节介绍了谢洪赉学习代数和使用该书的感受。谢洪赉称其初学代数时使用的教科书是《代数备旨》，但在接触应用题之前，他不明白代数之用，并因此心生厌倦。他指出《最新中学教科书代数学》一开始就有应用题，使他学习兴趣盎然，且他的同学也都有同样的感受。可见他认识了到该书贴合学生学习心理、注重学生学习兴趣的特点。

第五、六节比较简短，前者介绍对人名和度量衡的本土化，后者介绍该书的翻译经历。谢洪赉称他在教学之余仅用不到100天就完成了该书的翻译，因此难免存在错误，并希望读者指出错误，以便再版更正。

《最新中学教科书代数学》的译例类似现代数学教科书的前言。谢洪赉通过引用米尔恩的介绍与记述自己的感悟，指出该书的归纳法特点和诸多优点。他对归纳法的介绍，以及对改良数学教科书的期待，反映出他进步的一面。

3.3 编排、符号和术语的选用

在《最新中学教科书代数学》出版前，国内已有采用横排、用英文字母指代未知数的代数教科书，如武昌中东书社出版的《最新代数教科书》。但谢洪赉仍将底本中的英文字母改为天干地支等汉字，并采用自右向左、竖排的编排。他之后翻译的几本数学教科书也采用了类似的符号和编排，反映了他保守的一面。

在名词术语的选用上，谢洪赉秉持从旧的原则，除非必须，不然不创设新名词。他在翻译《最新中学教科书几何学》时，提及了其译名选取原则：

本书名目，大率袭用《几何原本》《形学备旨》之旧，以是二书，吾国学界沿用已久也。间有一二改定者，则有不得不改之故，其本未有定名者，不得已始创立一二。［25］

谢洪赉编译《最新中学教科书代数学》时，沿用的应是狄考文编译《代数备旨》中的译名，同时自创了个别译名以补《代数备旨》之缺。《代数备旨》《最新中学教科书代数学》中部分名词术语的译名与英文名、今译名的对比情况见表2。

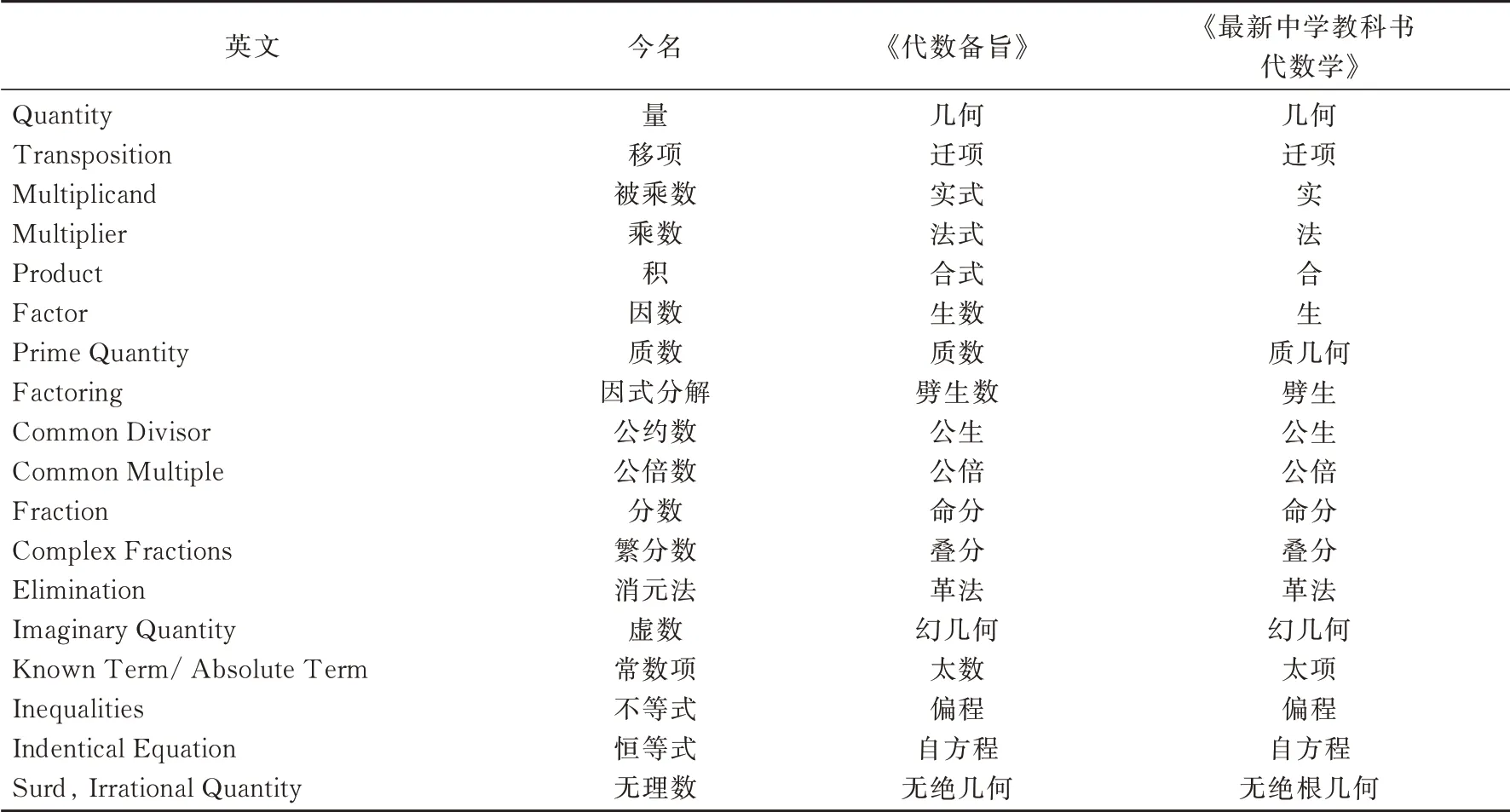
表2 《代数备旨》《最新中学教科书代数学》部分名词术语与今译名、英译名对照表Tab.2 Comparison of Daishubeizhi， High School Algebra′s Chinese version and English and modern Chinese in terminology

狄考文常常借用中国传统数学中的名词作为代数术语，如用“实”“法”“和”指代被乘数、乘数、积。他还将《代数术》所使用的“无理数”改为“无绝几何”，“消元”改为“革法”，“虚数”改为“幻几何”，“常数”改为“太数”等等［26］。虽然谢洪赉在译例中批评《代数备旨》不够完善，但他仍沿用了这些具有狄式风格的译名。这可能与《代数备旨》在当时比较流行有关，但也反映出他保守的一面。

谢洪赉学习过日文，称“凡从事译著者，不可不粗识日本文之意义及变化”［21］16，且他在编译1904年出版的《最新中学教科书物理学》时的确参考了日译名［27］。但他在编译《最新中学教科书代数学》时并没有参考日译名。

谢洪赉自创了一些译名，如在介绍笛卡尔符号法则（Descartes′ rule of signs）时出现的名词“号变”（variation of sign）和“号承”（permanence of sign）。“号变”指“相继二项之号相反”，“号承”指“相继二项之号相同”［1］下册271-272。但这两个概念比较生僻，没有得到广泛流传。

总的来看，谢洪赉翻译该书的缘起与目的体现出他求新的一面；但其翻译风格又显示出他保守的一面。这种矛盾使得《最新中学教科书代数学》兼有新旧两种元素，体现出他作为时代节点上的人物的纠结。

4 《最新中学教科书代数学》的流传与影响

《最新中学教科书代数学》装订成上下两册，被商务印书馆定为中学堂一至三年级的教材［28］，出版后风行一时。目前已知的出版情况见表3。

该书各版本的内容没有差异。第七版开始采用横排，但仍使用天干地支指代未知数。该书出版仅十个月即出至第三版，可见其一时之畅销。该书还见于《成都通览》所记录的书店销售书目，可见该书被商务印书馆在全国范围销售，对内地也有一定影响［29］。《申报》对该书评价道：

代数一术在算学中最为捷经，惜旧有译本非缺而不全、即繁而寡要，习畴人术者憾焉。是书系山阴谢君洪赉取美国最新教科本译成，由浅入深，步步引人入胜，学者苟能于各题悉心研究，于学算之术思过半矣。［30］

谢洪赉还翻译了《最新中学教科书几何学》（平面部、立体部）、《最新中学教科书三角学》《最新中学教科书微积学》。商务印书馆在宣传时称：

代数、几何、三角、微积自数学层累而上，如接替然。往时亦有各种译本，但阅时已久，其法未免陈旧，且成书非出一人，彼此体例各殊，不相联络，于学者拾级而登之兴味，亦未能充满。右四书……皆由谢洪赉君一手译成，不啻自成首尾，诚算学界不可多得之书。［31］

表3 《最新中学教科书代数学》各版出版日期Tab.3 Publication dates of High School Algebra′s Chinese version

作为当时少有的成套数学教科书，该宣传并不夸张。但《最新中学教科书代数学》在呈递学部审定时并不顺利。1909年12月3日，《学部官报》刊登对该书的审定意见为：“译笔虽甚晓畅，然其中名义有欠妥处，另纸批出，俟修改后再呈审定”［32］，该书并未直接通过审定。1910年8月，《图书汇报》将该书列入学部审定书目［33］，该书可能在此期间再次递审并通过。

进入民国后，《最新中学教科书代数学》逐渐无人问津。这与民国建立后晚清教科书大多停用或改版有关，但该书知识内容的设置、谢洪赉的翻译与该书的再版方式、谢洪赉对归纳法介绍的不足，也导致了它的淘汰。

首先，该书的知识内容不合国内学情。该书底本来自美国，而中美之间的差距使该书并不适用于晚清的中学堂。类似的，同样译自美国的《最新中学教科书物理学》《最新中学教科书几何学》也没有被中学堂采用，而是被浙江高等学堂的高等预备科采用［34］593。但对于高等学堂的代数课而言，《最新中学教科书代数学》的内容又偏少，如四川高等学堂的大代数课一开始就教行列式［34］616，而该书没有介绍行列式。此外，商务印书馆将该书作为中学堂一至三年级的教科书，而“癸卯学制”规定代数是二至四年级的课程，两者也有不合之处。

其次，谢洪赉在翻译时选用的编排、数学符号和名词术语，沿袭了1890年出版的《代数备旨》，相比译自日本的教科书，略显落后，商务印书馆在再版时也没有及时更新。在底本更新内容并再版后，商务印书馆和谢洪赉始终没有对译本进行修订。事实上，底本第二版增设“图解代数”章，反映了欧美数学教育强调几何与代数相结合等新思潮。谢洪赉和商务印书馆对其的忽视，实际上是错过了这一次革新，折损了该书自身的价值。此外，该书没有附教授法，这甚至不符合现代教科书的要求［35］。

最后，谢洪赉没有充分说明该书的归纳法特点，只提到归纳法能使学习循序渐进。读者可能无法充分理解该书的价值，如魏庚人就称，“独本书用归纳法进行教学，看不到它的优点”［2］61。而在晚清，新式教育初立，大部分教师仍是科举时代的童生、秀才、举人，缺乏受过师范教育的教师［36］，教育思想比较陈旧，对归纳法的接受可能更为困难。

在“癸卯学制”颁行初期、新式教育刚开始推行的节点上，《最新中学教科书代数学》旧的一面越发明显，而新的一面得不到广泛接受。对于它所处的时代和地点而言，该书有些不合时宜。因而该书虽然一时热潮，但没有产生深远的影响，以至于今天几乎找不到使用它的记录。

5 结语

1895年甲午战争后，中国兴起编译教科书的热潮，1904年“癸卯学制”的颁行则将这股热潮推向高潮。谢洪赉具有丰富的翻译经验，与商务印书馆关系密切，对数学也很重视。《最新中学教科书代数学》的问世是这一社会背景与谢洪赉个人情况综合作用的结果。该书底本为美国米尔恩编写的《中学代数学》。米尔恩具有良好的知识基础和丰富的教学经验，其《中学代数学》使用归纳法编写，内容设置比较规范，为《最新中学教科书代数学》的质量提供了基本保障。

谢洪赉在译例中介绍了《最新中学教科书代数学》的归纳法特点和诸多优点，说明了其翻译目的是为了向国内介绍用归纳法编写的教科书，以促进教科书改良。其翻译忠实底本，没有改动底本的结构内容，只将符号和编排改为旧式的，并采用一些编译策略以提高可读性。该书沿用了《代数备旨》中的名词术语，并自创了个别名词。总的来看，谢洪赉对该书的编译颇为用心。

《最新中学教科书代数学》应是国内出版的第一部用归纳法编写的中学代数教科书，对归纳法在中国的早期传播和改良中国中学数学教育起到积极作用。这是谢洪赉对中国近代中学数学教科书建设和中学数学教育发展做出的重要贡献。

客观而言，《最新中学教科书代数学》存在知识内容不合国内学情、翻译守旧且滞后、特点介绍不充分等问题。这反映了以谢洪赉为代表的一批教科书编译者的局限，即对知识内容的选取不统一，对现代数学的接受不彻底，对教科书编写思想的理解不充分。这种情况出现的原因，一是“癸卯学制”对课程的要求不具体，编译者无章可循；二是编译者深受旧式风格影响，自身思想没有彻底转变；三是西方教育学刚刚开始传入国内，国人对教育学的认识不足。随着新思想的传入和新教科书的涌现，《最新中学教科书代数学》遭到淘汰是必然的。该书出版之际，中国正处于中学数学教科书的由传统向现代的过渡时期，该书的选材、翻译方式和遭遇，可视为该过渡时期的一个典型。

作为一部略显不合时宜的教科书，《最新中学教科书代数学》没有产生深远影响，其强调的归纳法在晚清也没有立刻引起反响。到19世纪20年代，在欧美教育思想广泛传入，有了一定思想基础后，归纳法逐渐得到重视。1923年的《小学算术课程纲要》、1929年的《初级中学算学暂行课程标准》等都强调归纳法的使用［37］，并出现了国人自编的使用归纳法编写的数学教科书。这说明，一部合适的教科书，不仅要在知识内容上合格，其编写思想和方法也要符合当时的社会、教育状况。而外国教科书多少有与国情不符之处，因此，翻译和编译教科书只是过渡，最终还是要“国化教科书”［38］。