十字型微谐振梁多场耦合非线性振动分析

2023-02-01许立忠

振动与冲击 2023年1期

韩光，许立忠

(1.燕山大学机械工程学院，河北秦皇岛 066004;2.河北建材职业技术学院机电工程系，河北秦皇岛 066004)

微机电系统(micro electro-mechanical system，MEMS)具有集成化、微型化、智能化、易批量生产以及精度高、功耗小等特点。现已广泛应用于智能制造、物联网、工业电子、机器人、生物医疗以及消费电子等领域，是当今科技研究的热门方向之一[1-3]。在MEMS领域，微谐振传感器的市场和发展潜力最大[4-6]，微谐振传感器已广泛应用于航空航天、无人驾驶等领域[7-9]。

在微谐振传感器的设计中，为了提高传感器的精度、灵敏度及稳定性，谐振梁的合理设计尤为关键。Thomas等[10]通过对谐振梁进行合理优化，采用谐振微悬臂梁阵列传感器测量生理条件下蛋白受体的相互作用，并测定了细菌病毒T5在亚柱浓度下的结合量。对研究跨膜蛋白受体及其配体之间的相互作用具有重要医学意义。Zhao等[11]提出了一种同时修改谐振梁的表面轮廓和横截面类型以优化其刚度和质量分布的方案，以提高传感器的灵敏度。许高斌等[12]通过对谐振梁的两边增加了侧梁,提高了传感器的稳定性,并且进一步优化传感器检测灵敏度。在仿真平台下其传感器基础谐振频率为29.834 kHz，在0～120 kPa范围内灵敏度可达29.6 Hz/kPa。Rajanna等[13]利用溅射沉积方式在氧化铝阳极表面形成谐振膜，并将谐振膜作为压力传感器应变片，通过该工艺得到的谐振薄膜式压力传感器可以检测0～10 bar范围内的压力值。

谐振梁是微谐振传感器关键部分，但工作时广泛存在着非线性因素，因此谐振梁的多场耦合非线性振动研究对谐振传感器设计与应用具有重要的指导价值。刘敏等[14]提出了基于独立变分模态分解与多尺度非线性动力学参数的特征提取方法，极大地提高了机械故障诊断准确率。刘燕等[15]考虑到谐振梁的非线性效应，运用林滋泰德-庞加莱法，计算求解动力响应。Javadi等[16]在欧拉-伯努利梁理论的基础上，利用Hamilton原理推导了具有非线弹性基础和拉伸引起的Von Karman非线性的控制方程，采用伽辽金投影法将这些非线性偏微分方程简化为非线性常微分方程，这为传感器设计与应用提供了理论基础。

综上所述，基于对微谐振传感器方面做出的大量研究工作，动态特性是保证谐振传感器工作性能的关键。在微谐振传感器中，电容检测法与电阻检测法相比，降低了检测电路的制造难度。因此得到了广泛的应用。然而，现有微谐振传感器中的谐振梁与下极板之间的电容非常小，那么谐振时电容变化信号很小，增加了后续放大电路的制作难度。

为此，本文提出了一种十字型微谐振梁，可应用于压力传感器。压力传感器依靠感知谐振梁内部轴向力的变化来测量外部压力。由于十字型谐振梁增加了极板的面积。通过增加微谐振梁与下极板之间的电容，增加了信号的强度。降低了后续放大电路的设计难度。因此较两端固支等截面梁更有优势。使用Owen交流电桥进行检测。同时创新性的采用隔离带将激振端和拾振端分开，以便输出的电压信号中不会掺杂激励信号，结果更加真实准确。对于具有十字型谐振梁的微型谐振传感器，谐振梁的动态特性仍然是决定其性能的关键。因此，本文建立了十字型微谐振梁的多场耦合动力学方程，并求出了十字型微谐振梁非线性振动固有频率表达式。研究了十字型微谐振梁固有频率随激励电压变化规律，分析了分子力对十字型微谐振梁固有频率的影响。并且研究了十字型微谐振梁不同参数对其位移响应的影响。最后利用实验测试结果与理论分析值对比，证实了非线性振动理论研究的正确性。

1 动力学方程

根据谐振梁的工作原理，谐振梁单元多场耦合物理模型如图1所示。模型分为谐振梁与下极板两部分，两原件均为单晶硅制成。谐振梁长度为2l，宽度为b，厚度为h，弹性模量为E，材料密度为ρ。本模型为细长梁，属于欧拉—伯努利梁，因此可忽略梁横截面的剪切变形和转动惯量。谐振梁只产生在Y向的位移y(x,t)。

根据振动理论[17-18]，谐振梁多场耦合动态振动方程为

(1)

式中：F为谐振梁上的轴向力(N)；g为作用在单位长度谐振梁上的全部载荷(N/m)；I(x)为横截面对中心轴的惯性矩；S(x)为谐振梁横截面积。

为便于分析谐振梁的振动特性，将Y向的位移y(x,t)分为静态位移与动态位移两部分，即梁上任意一点某时刻的位移为

y=y0+Δy

(2)

式中：y0为谐振梁的静态位移(N/m)；Δy为谐振梁的动态位移(N/m)。

载荷g包括电场力和卡西米尔力两部分，即

g=fe+fc

(3)

式中：fe为单位长度上的电场力(N)；fc为单位长度上的卡西米尔力(N)。

单位长度上的卡西米尔力为

(4)

式中：hc=hp/2π；hp为普朗克常数(Plank constant)；cc为光速(m/s)；d0为极板间隙(m)。

考虑卡西米尔力非线性因素，将卡西米尔力在y=y0处进行泰勒级数展开，得到

(5)

泰勒展开式的第一项为作为静态卡西米尔力项。省略三阶以上高阶项，其泰勒展开式的余项作为动态卡西米尔力项。

静态卡西米尔力的表达式为

(6)

动态卡西米尔力的表达式为

(7)

其中：

设式中非线性分析小参数为

(8)

单位长度上的电场力为

(9)

式中：U为施加在谐振梁与下极板间激励电压(V)；εo为真空电容率(F/m)；εr为相对电容率。

在y=y0处，对电场力的表达式泰勒展开，有

(10)

同理可得

静态静电力的表达式

(11)

动态静电力的表达式

(12)

其中：

将式(12)、式(7)代入式(3)可得动载荷为

Δg=εξ1Δy+εξ2Δy2+εξ3Δy3

(13)

2 系统非线性自由振动

在振动中，将产生动态位移Δy，即产生动态的静电力与卡西米尔力。线性项与非线性项都包含动态位移，因此其对线性与非线性的固有频率都有影响。

将动态位移Δy及式(13)代入式(1)可得谐振梁多场耦合非线性振动方程为

εξ1Δy+εξ2Δy2+εξ3Δy3

(14)

令Δy=φ(x)q(t)并代入式(14)可得

(15)

式中：q为广义坐标；q″为广义加速度；φ为模态函数；

(16)

其中：

式(15)右边为

(17)

由式(17)化简为常系数微分方程

(18)

式(18)的特征方程为

s4-α2s2-β4=0

(19)

式(19)的四个特征根为

其中：

则式(18)的通解为

(20)

将谐振梁简化后的力学模型如图2所示。将梁的中部结构简化为质量块m，梁的总长度为2l。分别以微梁的左右两端点O1、O2为原点设立两个局部坐标系。梁左侧坐标系x轴方向以右为正方向，梁右侧坐标系x轴方向以左为正方向。y轴方向与原坐标系方向相同。设局部坐标系下左梁的模态函数为φ1(x)，右梁的模态函数为φ2(x)。在x1=x2=l处φ1(x)与φ2(x)呈奇函数或偶函数对称。根据文献[19]所述此类型模态函数如式(22)、(24)所列。

图2 简化的谐振梁结构动力学模型Fig.2 Simplified resonant beam dynamics model

左梁φ1(x)和右梁φ2(x)呈奇函数对称时，频率方程为

(21)

模态函数为

(22)

其中：

左梁φ1(x)和右梁φ2(x)呈偶函数对称时，频率方程为

(23)

模态函数为

(24)

其中：

将式(16)的解展成ε的幂级数

q=q0+εq1+ε2q2+…

(25)

将系统非线性自由振动频率ω展成ε的幂级数

(26)

引入新的自变量τ=ωt得

(27)

将式(27)代入式(16)得

(28)

将式(25)、式(26)代入式(28)，令ε的同次幂的每一项系数为零，可得

(29)

(30)

(31)

初始条件如下

(32)

式中,k0为初始广义位移(m)。

由式(29)与式(32)解出

q0=k0cosτ

(33)

将式(33)代入式(30)得

(34)

为避免式(34)的解中出现久期项，令方程右边cosτ项的系数等于零，导出

(35)

将式(32)、式(35)代入式(34)解得

(36)

将式(33)、式(35)代入式(31)解得

(37)

为避免式(37)的解中出现久期项，令方程右边cosτ项的系数等于零，导出

(38)

将式(32)、式(35)、式(38)代入式(37)解得

(39)

将式(33)、式(36)、式(39)代入式(25)解得

(40)

将式(35)、式(38)代入式(26)，解得非线性系统自由振动幅频相应关系为

(41)

3 实例计算与分析

3.1 频率特性分析

谐振微梁的主要参数如表1所示。联立式(18)、(19)、(21)、(23)可求解谐振微梁各阶线性固有(角)频率ω0。将ω0代入式(41)中，可求得相应的谐振微梁非线性各阶固有(角)频率值ω。表2为谐振微梁静态位移改变时，其线性与非线性各阶固有频率值。其中fa为线性固有频率值，fb为非线性固有频率值。其中η为两者的相对误差。表3为谐振微梁非线性振动随偏置电压的变化规律，其中η为两者的相对误差。考虑与忽略卡西米尔力情况下各阶非线性固有频率如表4所示，其中f1为忽略卡西米尔力各阶非线性固有频率数值，f2为考虑卡西米尔力的各阶非线性固有频率数值。其中η为两者的相对误差。在考虑卡西米尔力的影响下，线性与非线性各阶固有频率情况如表5所示，其中f3为考虑卡西米尔力的各阶线性固有频率数值，其低阶模态如图3所示。由表2～5及图3可见：

(1) 随着静态位移的逐渐增大，系统线性固有频率降低。

(2) 随着静态位移的逐渐增大，系统的非线性固有频率也降低。且静态位移对非线性固有频率的影响更为明显。

(3) 当偏置电压增大时，谐振微梁的固有频率下降，且低阶的固有频率下降的更为明显。

(4) 当考虑非线性对谐振梁的影响时，固有频率值低于线性频率值，从低阶到高阶非线性与线性的频率差值逐阶减小，其中第一阶非线性与线性的频率差值约为第三阶的8倍。

(5) 偶数阶比奇数阶非线性与线性的频率差值更大，其中偶数第一阶约为奇数阶的1.4倍，之后随着阶数的增加奇数阶与偶数阶的频率差值逐渐相近。

(6) 当考虑卡西米尔力对谐振梁的影响时，其固有频率值低于不考虑时的频率值，这是因为在振动过程中卡西米尔力可以等效为软弹簧系统，从而导致了固有频率的降低。且卡西米尔力对低阶固有频率的影响明显高于高阶。其中奇数第一阶考虑与忽略卡西米尔力的频率差值约为第三阶的5倍。

(7) 在考虑卡西米尔力时偶数阶比奇数阶的频率差值更大，随着阶数的增加奇数阶与偶数阶的频率差值逐渐相近。

(8) 在模态函数为奇函数时，其形式呈反对称型。当在模态函数为偶函数时，形式为对称型。谐振梁的位移峰数随着阶数的增加而增加。对于相同阶数，反对称模态的固有频率要大于对称模态的固有频率。

(9) 当模态函数为反对称型时，谐振梁中心的振动位移始终为零。对于对称型模态，其中心的振动位移不为零。一阶对称模态，谐振梁中心处的振动位移最大。

表1 系统参数Tab.1 System parameters

表2 不同静态位移，各阶自由振动线性与非线性固有频率比较Tab.2 Comparison of linear and nonlinear inherent frequencies of free vibration for changing static displacement

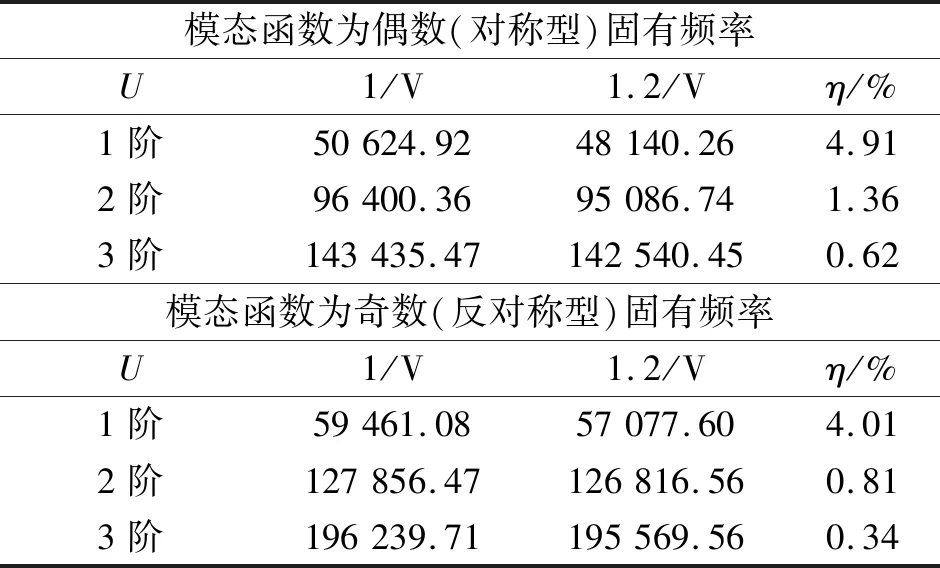
表3 随偏置电压改变的非线性频率变化规律Tab.3 Changes of nonlinear frequencies with voltages

表4 分别考虑和忽略卡西米尔力时，各阶自由振动非线性固有频率比较Tab.4 Comparison of inherent frequencies of free vibration for considering and ignoring Casimir force respectively

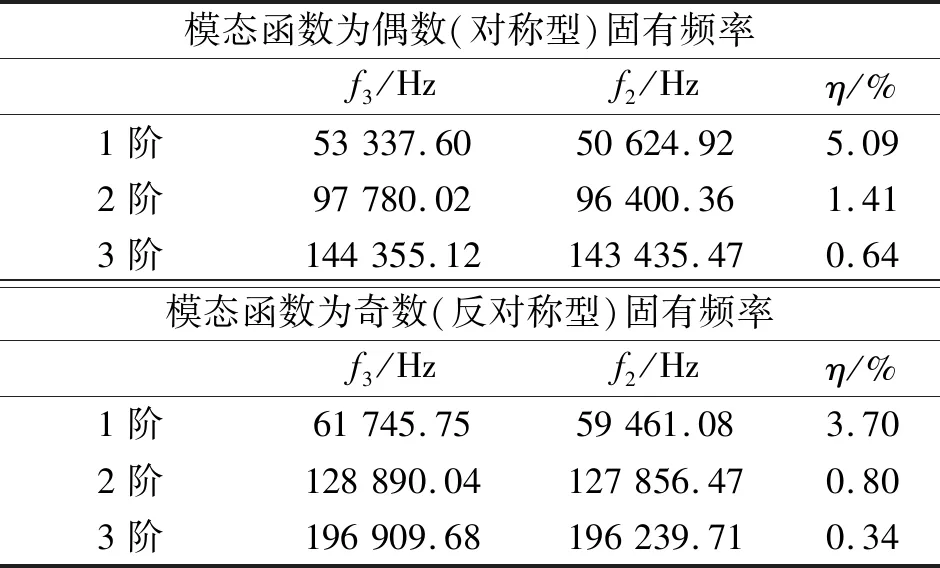
表5 考虑卡西米尔力时，各阶自由振动线性与非线性固有频率比较Tab.5 Comparison of linear and nonlinear inherent frequencies of free vibration for considering Casimir force

(a) 对称型一阶模态

3.2 时域分析

为了研究不同参数对谐振梁时域动态响应的影响，改变谐振梁长度、宽度、厚度、极板间距和质量块的质量等参数，观察谐振梁中点位移一阶时域响应随时间的变化规律，结果如图4所示。由图4可知：

(1) 改变谐振梁的长度，其他参数不变时。随着谐振梁长度的增加，谐振梁的振幅增大，振动周期增大。这是因为谐振梁的刚度减小，谐振梁有了更大的初始位移。

(2) 当改变谐振梁的宽度时，随着谐振梁宽度的增加，谐振梁的振幅减小，振动周期增大。

(3) 当改变谐振梁的厚度，其他参数不变时。随着谐振梁厚度的增大，谐振梁的振幅减小，振动周期减小。

(4) 只改变极板间距，当增大两极板间距时，谐振梁的振幅增大，振动周期减小。

(5) 随着质量块的质量增大，谐振梁的振幅增大，振动周期也增大，这是由于质量增加引起惯性力的增大。

(a) L变化

3.3 实验分析

在传感器设计中谐振梁的振动频率为核心参数之一，它对传感器的性能有着决定性影响。为了验证上述关于谐振梁振动频率理论分析的正确性，采用微机械加工技术制作十字型微谐振梁样件并测试。

微谐振梁加工工艺流程如图5所示。基材选用直径2英寸单晶硅片，使用超声波去离子水对硅片进行清洗。使用匀胶机将正性光刻胶均匀涂于硅片上下表面，光刻胶层厚度为10 μm。采用紫外线光刻技术将掩膜版上的目标图案转移到光刻胶层上。经紫外线曝光过的光刻胶会发生化学性质的改变，溶于相应显影液中。将有胶层的硅片浸入质量分数为0.26 N浓度TMAH显影液中，直至曝光图案完全呈现。此时剩余的光刻胶层会对部分二氧化硅进行覆盖保护，使用氢氟酸对未覆盖光刻胶层的二氧化硅进行腐蚀。

腐蚀结束后，光刻胶的目标图案转移到二氧化硅层上，此刻的二氧化硅层起到了对硅的选择性保护的作用。选用高浓度TMAH腐蚀溶液对硅基材进行腐蚀加工，待腐蚀到所需深度后，腐蚀加工结束。最终得到目标形状的三维结构。为增强谐振梁的导电能力，需在谐振梁表面镀厚度为400 nm的金导电层。谐振梁结构如图6所示。下极板加工流程与上极板类似，依次采用光刻、腐蚀、镀导电层的加工工艺。

图5 谐振梁加工工艺Fig.5 Fabrication process of resonator

采用电子束光刻胶连接上下极板，并通过控制涂胶转速与时间可以精确获得100 nm的胶层，可获得300 nm的极板间隙。选取立方体铝材为支撑底座，使用UV胶将下极板固定在底座上。利用导电岩浆在极板上进行引线，引线材料为直径25 μm的高纯铜线，铜线的一端采用导电岩浆固定在极板上，另一端焊接在电路板接线柱上便于进行测试。

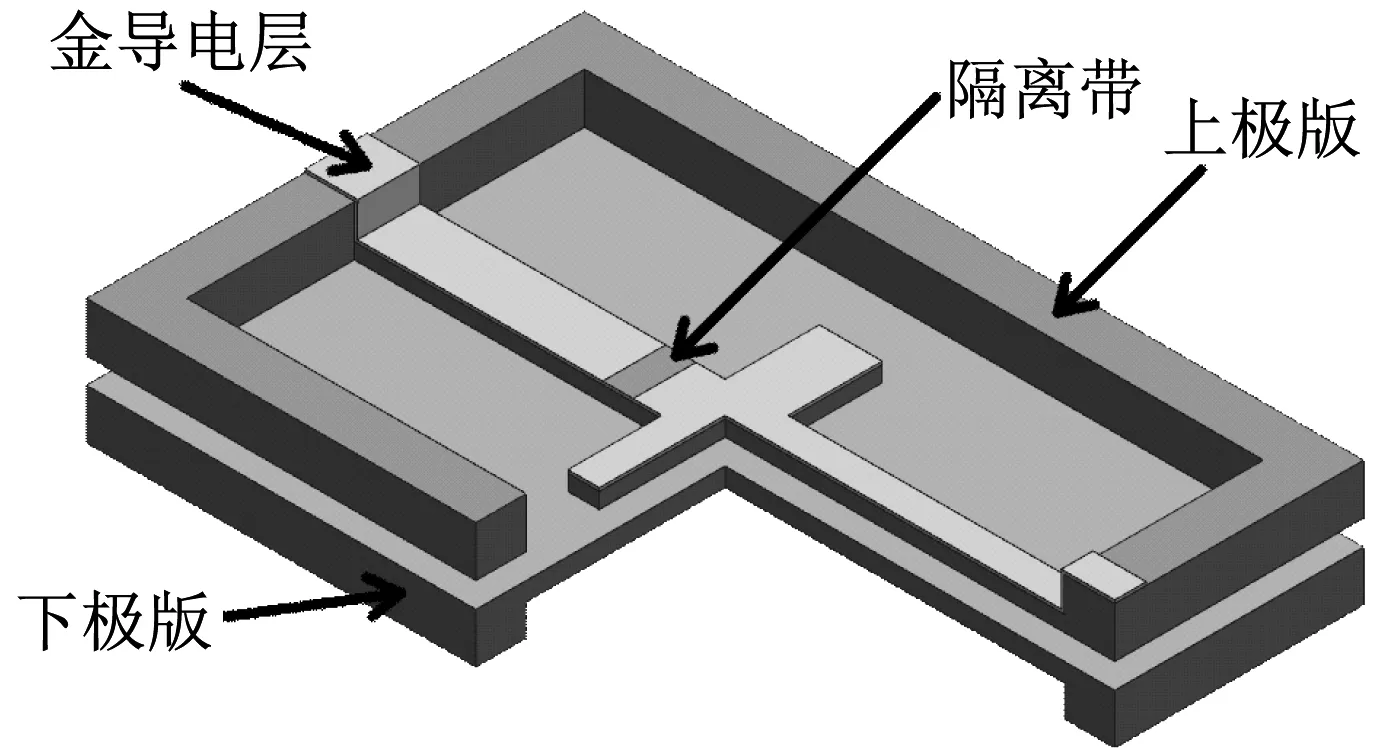
图6 谐振梁结构示意图Fig.6 Structures of resonator

自制十字梁与一字梁谐振器如图7、图8所示，其尺寸如表6所示。

图7 十字梁及谐振器Fig.7 Cross beam and resonator

图8 一字梁及谐振器Fig.8 Straight beam and resonator

表6 谐振梁系统参数Tab.6 Resonant beam system parameters

采用自主设计的测试系统进行了以下测试。本实验采用静电激励—电容检测的方法进行振动频率的测量检测，其原理图如图9所示。谐振器可以等效为平板电容器。采用lift-off工艺制隔离带将激振端与拾振端分开，且拾振端分配面积更大，便于获取检测信号。对开环系统施加静电压激励信号，通过调节可调电阻Rref和可调电容Cref，使电桥达到平衡。此时a、b端的电压差为零，系统无信号输出。当施加交流激励电压时，极板间的静电场力产生周期性变化，进而传感器的等效电容值发生周期性变化，谐振梁受静电场力的作用相对下极板发生周期性位移。此时电桥平衡状态被打破，a、b端产生周期性电压差，传感器的位移信号转化为电信号，通过owen交流电桥将电信号传入100倍的微弱信号差分放大器输出到频谱仪上。当谐振梁固有频率接近激励频率时产生共振现象，此时输出的电压信号最强且位移响应为最大值。

图9 开环测量系统Fig.9 Open loop measurement system

实验现场照片如图10所示。由信号源施加激励信号在激振端，以驱动谐振梁产生振动。在拾振端拾取此谐振梁的振动信息，并把这个振动信息转化为电压信号，由频谱仪检测此电压信号来获取梁的振动信息。

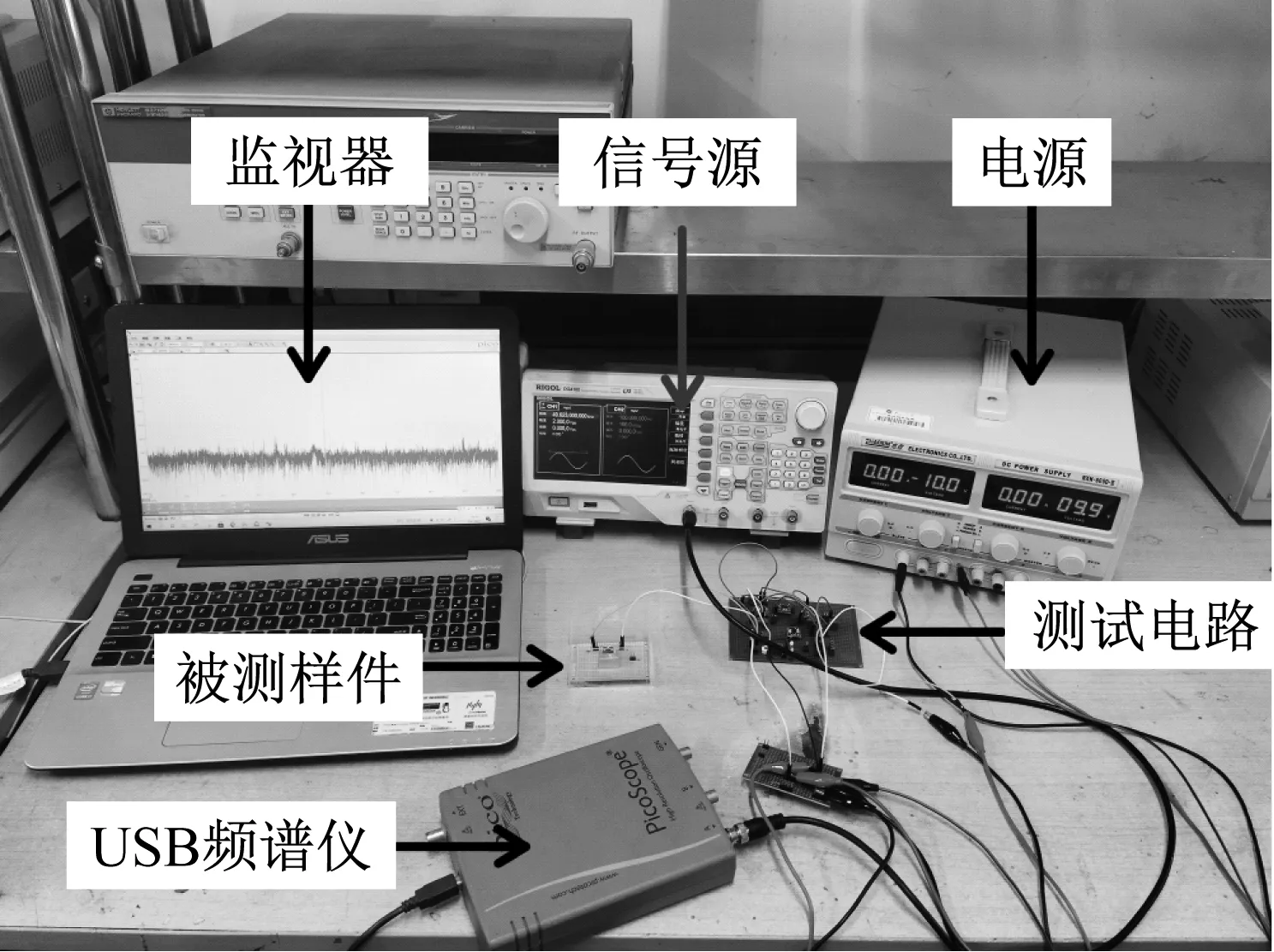
图10 实验现场图Fig.10 Experimental site map

(42)

求得十字梁的品质因子Q为105.8，满足传感器的实际应用[20]。在相同实验条件求得一字梁品质因子为63.6。结果表明十字型谐振梁的品质因子明显高于一字型梁的品质因子。

图11 开环扫频幅频特性曲线Fig.11 Amplitude-frequency curve for open loop scanning

采用频率为49 627.38 Hz的激励源对十字梁进行激振，十字梁输出信号的频谱图如图12所示，在谐振频率附近的信号强度较为明显，其信号强度为-46 dbu。同理测得一字梁的信号强度为-61 dbu。其信号强度优于传统一字梁[21]信号，其原因为十字型谐振梁的面积更大，使其基础电容增大，信号更强。且由于中部质量的增加，提高了振幅，从而进一步增强了信号。因此其更有利于应用到微纳传感器当中。