高层建筑围护结构风压系数的概率特征及其极值POT估计

李寿科，毛 丹，刘 敏，郭 凡，孙洪鑫，陈元坤，邓声祥

(1.湖南科技大学 土木工程学院，湖南 湘潭 411201；2.中南建筑设计院股份有限公司，武汉 430071；3.江西省建筑设计研究总院集团有限公司，南昌 330046)

相对于主体结构而言，建筑的围护结构更易受到风致破坏，其围护结构设计风荷载计算是风工程研究的重点和热点[1]。围护结构设计风荷载计算中的重要步骤是估计结构表面风压系数极值。风压系数极值估计基于经典极值理论进行，认为极值样本通常收敛于常用的三种经典极值分布，可统一为广义极值分布。当母体服从高斯分布时，Davenport的研究表明其极值计算方法可采用具有解析表达式，可实现短样本长度的极值估计。然而，风压信号并不完全符合高斯分布[2-4]。Yuan等[5]对建筑表面风压进行研究时也发现表面风压并不是完全服从高斯分布。当风压分布为非高斯时，Sadek等[6-7]的研究发现表面风压的母体概率分布拟合可以基于Gamma分布进行，其极值估计基于考虑母体分布的转换过程法进行。基于Hermite矩方法也可认为是一类基于母体分布的转换过程方法，在工程中有较好应用[8-10]。

经典极值理论进行极值估计无需考虑样本的母体分布，只需拟合其极值分布，以渐进极值理论为基础。Gumbel分布是极值求取中使用最为广泛的一种极值分布，然而，Holmes的研究表明采用GEV(general extreme value)分布可以更好的描述表面风压的极值分布[11]。Liang等[12]研究表明部分测点的围护结构表面风压概率密度函数宜描述为正态分布与GEV分布函数加权组成的双峰概率密度函数。在考虑风压极值样本概率特征的基础上，学者对经典风压系数极值估计方法做了很多改进。全涌等[13]提出了改进Gumbel法，其能使用单个标准长度风压时程计算极值。李寿科等[14]仿真单次风压时程得到多段风压时程，用以计算峰值因子。Simiu等[15]提出一种峰值超越阈值(peak over threshold,POT)方法来解决区组数浪费的问题，用于极值风速估计。李正农等[16]检验广义Pareto分布的可靠性，得到广义Pareto分布无论在高斯以及非高斯样本情况下均能得到可靠极值的结论。Ding等[17]衡量基于短时距样本的极值计算方法，POT方法、平均条件穿越率法，转化法等的准确性，指出极值估计方法的不确定性主要由样本量决定。然而，POT极值估计方法在水文领域已有广泛的应用。对于当前POT极值估计方法，一直存在阈值选取困难的问题，致使该方法在风工程领域并未得到广泛应用。

本文首先对CAARC标准高层建筑进行刚性模型测压风洞试验，研究其表面风压系数的概率特征；然后提出一种改进的POT极值估计方法，进而与其他估计方法进行对比研究，证明当前改进POT方法的有效性和优越性；最后基于改进POT方法对CAARC标准高层建筑表面风压系数进行极值估计，给出其表面风压系数极值的分布规律。本文以CAARC模型展开研究，本文方法也可适用于其它实际工程的不同形状的建筑。

1 风洞试验概况及数据处理

试验于湖南科技大学风工程试验中心内完成，该试验中心风洞为开口直流吸入式矩形截面风洞，试验段长×宽×高为21 m×4 m×3 m，如图1所示。模拟了GB 50009—2012《建筑结构荷载规范》[18]规定D类地貌，风剖面指数α为0.30。风场缩尺比采用1∶400，参考高度45 cm，参考风速为10.2 m/s。高层建筑标准模型(CAARC)足尺尺寸长×宽×高为45.72 m×30.48 m×182.88 m，选用模型缩尺比为1∶400，模型尺寸为114 mm×76 mm×457 mm。高层建筑标准模型上总共布置有308个测压点。将高层建筑标准模型立面定义为E、N、W、S四个面，具体立面、试验风向角定义以及模型测点布置，如图1所示。在0°、45°两个典型风向角下，对高层建筑模型，独立重复采样200次，单次采样时间为30 s，采样频率为330 Hz，每个测点单次采样数为10 000个。

测压点的风压系数Cp,ij

(1)

平均风压系数Cpmean为

(2)

式中：Cp,ij为测点i在j时刻的风压系数；N为测点i的数据总数。

极值风压系数Cpmin、Cpmax为

(3)

(4)

式中，Pmin、Pmax为单个区组中最小、最大的风压。

2 表面风压系数概率特征

2.1 风压系数的高阶矩分布

风压系数极值估计常基于经典极值理论进行。当风压系数服从高斯分布，其概率分布可采用前二阶矩描述，其极值可以采用Davenport提出的峰值因子法进行极值估计。然而，高层建筑表面风压系数受到来流湍流、特征湍流等因素的影响，并不完全服从高斯分布，即其风压系数的高阶矩峰度不等于3、偏度不为0。

图2中给出典型风向角下，风压系数偏度分布图。0°风向角下，在迎风面N立面，风压系数偏度均大于0，右偏，极值风压系数在右边有较长的尾部，更易出现较大的极大值风压系数；建筑侧面、背风面风压系数偏度均小于0，为左偏，左侧有较长的尾部，极小值风压系数较小值出现概率较大。在45°风向角下，在迎风面积较小的W面靠近交接处会出现负值的偏度，即可能出现绝对值较大的极小值风压系数，其他立面分布规律与0°风向角时较一致。可以看出，尾流的旋涡脱落区易形成高偏度风压系数。

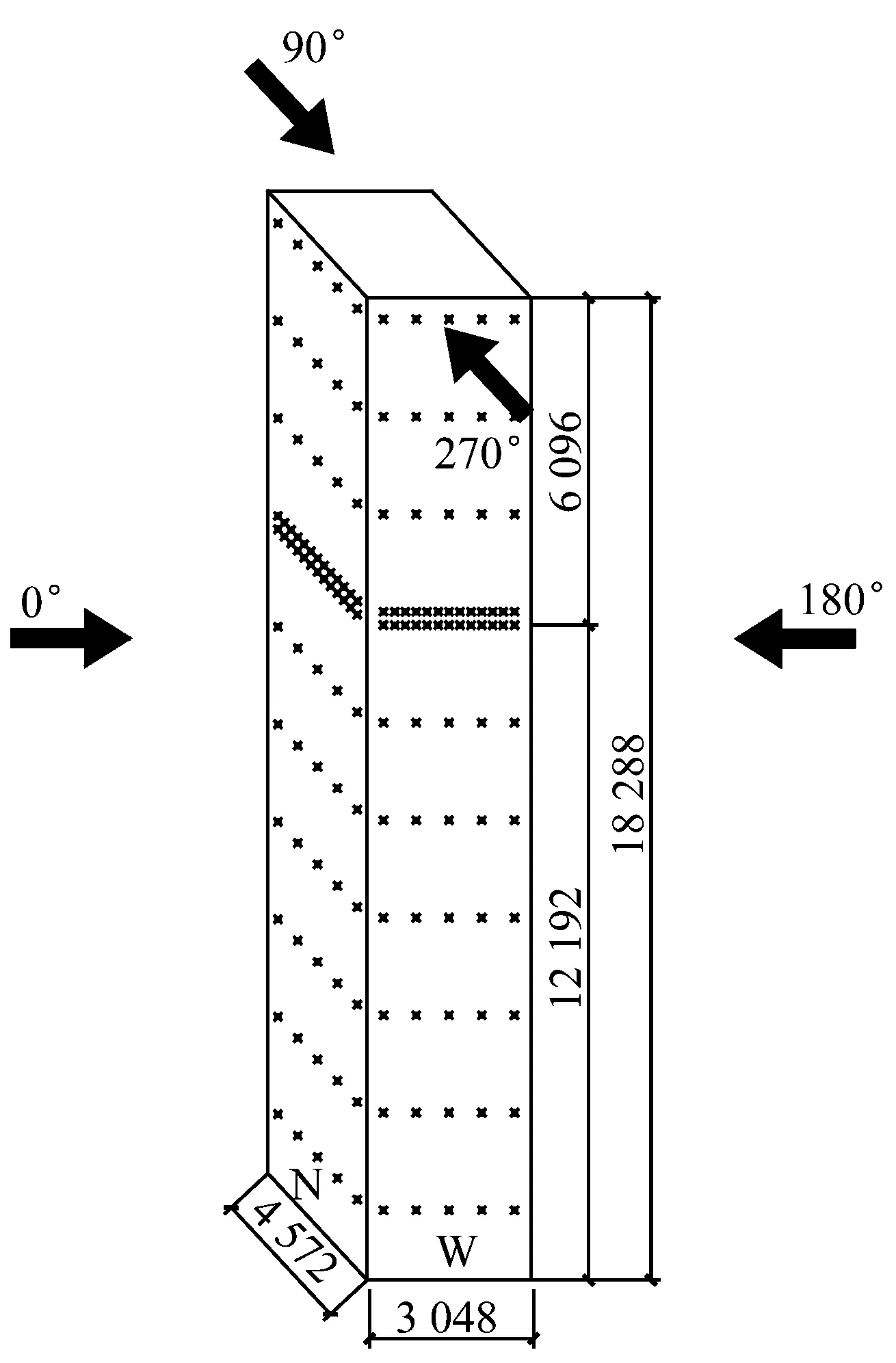
(a) 风向角定义图

(a) 0°风向角

图3给出了不同建筑立面的风压系数峰度。由图3可以看出，在0°风向角和45°风向角下，迎风面或迎风位置的峰度接近3，而其余位置则较明显的偏离高斯分布，0°风向的侧面其峰度明显大于3，45°风向尾流角部区位置的风压系数峰度也明显大于3，总结其规律可以看出尾流的旋涡脱落区易形成高峰度风压系数。

图4给出了两个典型风向下的偏度和峰度的散点图。由图4可以明显看出，对于0°和45°风向，基于文献[4]的非高斯测点分区方法，大部分测点都属于中度非高斯测点，少部分为强非高斯和弱非高斯测点。

2.2 风压系数的概率分布拟合

2.2.1 单次采样风压系数的概率分布拟合特征

图5给出了0°风向角下，两个典型测点单次采样风压系数的概率密度曲线拟合结果。由图5可以看出，测点11、测点29的概率密度曲线拟合与几种常用的概率分布中的Gamma分布拟合较好；不服从正态分布，这与前面的峰度和偏度分析结果一致；与对数正态分布也有一定的偏差，由于其具有较高的峰度，与GEV分布相差较大。

(a) 0°风向角

(a) 0°风向角

(a) 测点11

2.2.2 多次采样极值风压系数的概率分布拟合特征

图6和图7分别给出了0°风向角下，两个典型测点200次采样风压系数极值的概率密度曲线拟合结果。由图6可以看出，测点11风压系数极大值的概率密度曲线拟合与几种常用的概率分布中的Normal分布拟合较好；与Gamma、Lognormal、GEV分布的拟合偏差较明显。测点29风压系数极大值的概率密度曲线拟合与几种常用的概率分布中的GEV分布拟合较好；与Normal、Gamma、Lognormal分布的拟合偏差较明显。

对于风压系数极小值，总体来说，测点11和测点29风压系数极小值的概率密度曲线拟合与几种常用的概率分布中的GEV分布拟合较好；与Normal、Gamma、Lognormal分布的拟合偏差较明显。

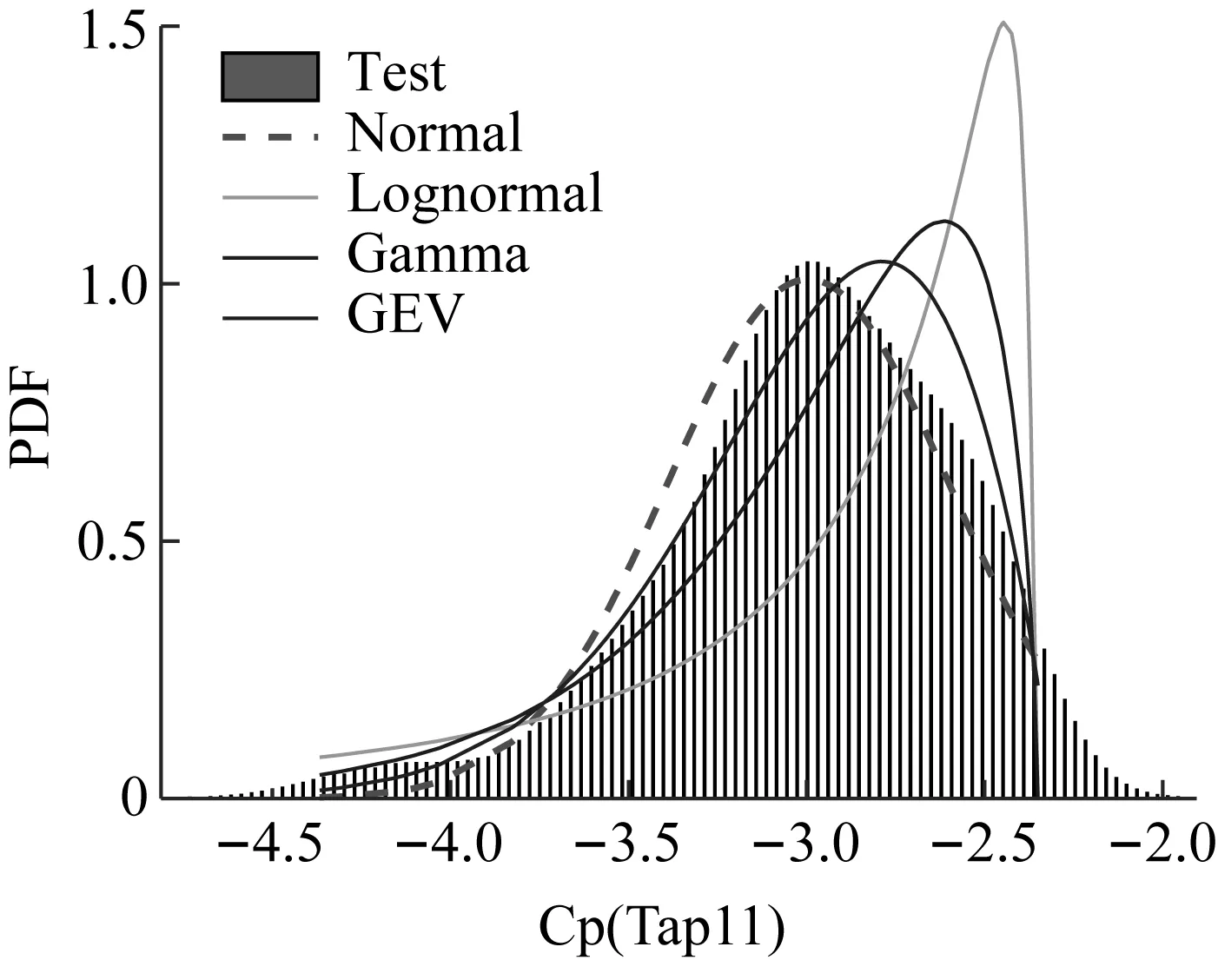
(a) 测点11

(a) 测点11

3 表面风压系数极值估计

3.1 改进POT极值估计方法

3.1.1 概率模型

服从独立同分布的数据，Pickands[19]研究表明超过阈值u的数据样本，也称为超阈值，其概率分布将向广义Pareto分布收敛。即随机变量X的分布函数为

(5)

则称X服从广义Pareto分布，其中μ表示位置参数，ξ表示形状参数，σ表示尺度参数。GPD分布尾部分位数xp-GPD及重现期由式(6)和式(7)给出，即

(6)

(7)

式中：xp-GPD为GPD分布尾部分位数；n为独立数据总数；Nu为超阈值数目总数；λ为单位时间独立同分布数据数目。

3.1.2 参数估计

广义pareto分布的参数，可以用概率加权矩估计方法得到[20]，式(8)～式(12)给出两参数概率加权矩估计计算方法，位置参数μ使用阈值替代

(8)

(9)

(10)

式中，Wr代表总体矩的样本估计量，对于有限的样本大小，一致的矩估计(Wr)可以计算为

(11)

总体矩估计可以用Landwehr等[21]提出样本估计量Wr来替代

(12)

式中：Xi,n为超阈值的数据样本；n为样本数量。

3.1.3 阈值选取

基于POT极值估计对于GPD概率模型形状参数的稳定性需求，结合数学中的变点理论，对传统阈值选取方法进行改进，实现不受研究人员主观影响的自动阈值选取。具体步骤如下：

① 确定阈值范围的起始点。原始阈值范围需要尽可能包含所有风压系数，也要符合GPD的适用范围，因此起点选择风压系数的最小值，终点选择保证样本数据量高于5的阈值。

② 选取候选阈值的间隔。为了运算简便，将阈值间隔定为0.02，且保证每次有数据剔除，即保证超阈值样本有变化。

③ 衡量相邻阈值对应的形状参数变化情况。最佳阈值一般存在于形状参数趋于稳定区间内，因此在差值比的判断标准上，是能围绕0值波动，并且绝对值越小越好，这样的区间会有高概率存在最佳阈值。

④ 基于变点理论确定最佳阈值。在得到有高概率含有最佳阈值的合适阈值范围后，结合变点理论—局部比较法选择变点(阈值)，此方法根据潜在变点附近局部小区段的统计量在各个局部内的变化作为判断标准，并取变化最显著的点作为变点。选择局部小区段形状参数的二阶中心距(方差)作为统计量，判断变点(阈值)的位置，变点位置对应的阈值即为最佳阈值。

3.1.4 POT方法流程

改进POT极值估计方法具体使用流程如下：

步骤1负压区数据取反号(如有必要)；

步骤2基于均值超越方法提取峰值样本，保证样本独立同分布；

步骤3选择最佳阈值存在的合适阈值范围；

步骤4基于变点理论的局部比较法选取最佳阈值；

步骤5基于最佳阈值确定超越阈值样本，进行GPD分布拟合优度检验，进而确定POT极值。

3.2 典型测点的风压系数极值估计

本节中将使用200组样本极值拟合至GEV分布所得78%极值分位数作为标准极值，与其他极值估计方法与之对应保证率的分位数，衡量估计偏差、均方误差(均方误差=偏差2+方差)，通过偏差以及均方误差判断极值估计方法的准确性与稳定性。

图8给出了典型测点在不同样本大小下基于POT极值估计方法的结果与标准极值的偏差。由图8可以看出，对于这几个非高斯和高斯概率特征的典型测点，随着样本的增加其估计偏差快速下降，最终稳定在5%以内。图9给出了典型测点在样本量为5时，不同估计方法与标准极值的偏差。由图9可以看出，改进POT方法准确性较好，独立风暴法和改进Gumbel方法的估计偏差在10%左右，而假定样本为高斯分布的峰值因子法的偏差较大(会高达50%)。

图8 典型测点POT方法下不同样本大小时的极值偏差Fig.8 Bias of extreme estimation by POT method for different sample size

图9 典型测点不同方法下的极值估计偏差Fig.9 Bias of extreme estimation by different method for same sample size

基于模型的所有测点(308个)，采用不同样本大小(1～10组)的风压系数时程，利用不同方法估计风压系数极值。图10中给出所有测点不同极值估计方法的估计结果与标准极值的平均偏差，以及平均均方误差。

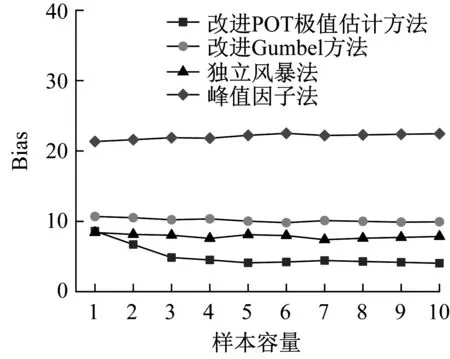
由图10(a)可以看出，改进POT极值估计方法的偏差均在10%以下，且随样本容量增加而快速减小，在样本容量为5组(甚至3组)及更多样本时，误差稳定在5%以下；而改进Gumbel法与独立风暴法误差非常接近，均在10%左右，且随样本容量变化较小；而基于高斯假定的峰值因子法偏差较大，约20%。

图10(b)给出不同极值估计方法的平均均方误差，在样本容量3以上时改进POT极值估计方法相较于其他方法平均均方误差小，说明改进POT方法估计总体上较为稳定；改进Gumbel法与独立风暴法均方误差较大，峰值因子法的均方误差最大。

综上所述，改进POT方法可用于风压系数极值估计，其样本量为5个30 s的时程，即可实现与标准极值小于5%的偏差，且稳定性好。

3.3 表面风压系数POT极值分布

图11给出0°、45°典型风向角下，基于POT方法的极小值风压系数等值线分布图。在0°风向角下，高层建筑迎风面N立面极小值风压系数较小，接近于0，范围为[-0.56，-0.09]；处于气流分离区建筑侧面E、W立面极小值风压系数较大，范围为[-4.59，-1.79]；背风面S立面风压系数极小值较小，且分布较均匀，范围为[-1.07，-2.23]。

(a)

(a) 0°风向角

在45°风向角下，建筑N、W立面的角部迎风，迎风面面积较大的N立面易出现来流再附，致使N里面极小值风压系数较小，极小值风压系数范围为[-2.06，-0.36]；而W立面则由于展向较短在边缘处迎风后，来流立即分离，使得W立面尾流区的极小值风压系数大于迎风区。处于背风面尾流区的E和S立面的极小值风压系数总体上较小，范围为 [-1.70，-2.04]。

4 结 论

对CAARC高层建筑刚性缩尺模型进行了测压风洞试验，研究了该高层建筑表面风荷载的概率特征，对其表面风压系数的母体分布和极值分布进行概率分布拟合，提出一种改进POT极值估计方法，与几种常用极值估计方法进行对比研究。结论如下：

(1) 在0°风向角和45°风向角下，迎风面或迎风位置测点风压偏度大于0，峰度接近3，风压分布接近正态分布，而其余位置则较明显的偏离高斯分布，0°风向的侧面其峰度明显大于3，45°风向尾流角部区位置的风压系数峰度也明显大于3，尾流的旋涡脱落区易形成高峰度风压系数。

(2) 典型测点风压系数母体不服从正态分布，其概率密度曲线拟合与几种常用的概率分布中的Gamma分布拟合较好；典型测点的极小值风压系数概率分布拟合采用GEV分布拟合较好。

(3) 改进POT方法可用于风压系数极值估计，其样本量为5个30 s的时程，即可实现与标准极值小于5%的偏差，且稳定性好。

(4) 0°、45°典型风向角下，受旋涡脱落和绕流的影响，CAARC高层建筑迎风区的极值风吸力接近0，在气流分离区的侧风面极值风吸力最大，背风面的极值风吸力分布均匀且较小。