基于惯容系统位置的调谐质量阻尼器的振动控制研究
2023-02-01刘欣鹏杨映雯晏致涛
刘欣鹏,杨映雯,孙 毅,晏致涛
(1.重庆科技学院 建筑工程学院,重庆 401331;2.能源工程力学与防灾减灾重庆市重点实验室,重庆 401331)
1909年Frahm提出[1]一种广泛用于结构振动控制的装置——调谐质量阻尼器(tuned mass damper,TMD),该装置由质量块、弹簧元件组成。为了扩大减振频带有效范围,Den Hartog等[2]在Frahm系统设计中增加黏性阻尼器。随着研究的深入,学者们发现应用于机械工程领域的惯容系统有着放大质量效应的优点。随后,Smith提出通过惯容系统连接TMD形成一种新型阻尼器——惯质调谐质量阻尼器(tuned mass damper-inerter,TMDI)[3],该装置能够改善TMD减振效率低、鲁棒性差的特性。
近年来,TMDI在建筑抗震、抗风及减振优化等领域受到了广泛的关注。在建筑抗震方面,Wang等[4-5]将惯容系统引入结构基础,以降低建筑悬架结构的振动响应;De Domenico等[6-7]利用TMDI特性,改善基础结构的抗震性能;Pietrosanti等[8]系统分析了TMDI在地震激励下的减震效率;Palacios-Quionero等[9]通过改进TMDI形式,提出MTMDI减震概念,并将其安装于两栋楼间,研究MTMDI对连体建筑的减震效率问题。
在结构抗风方面,Giaralis等[10]通过数值模拟74层建筑结构,研究TMDI对高层建筑风致振动的控制作用;Giaralis等[11]基于气动力经验功率谱,研究风激励作用下TMDI对于高层建筑风致响应的控制作用;王钦华等[12-13]通过开展刚性模型的风洞试验,研究TMDI及MTMDI对连体超高层建筑风振响应的控制效果。
在减振优化方面,Marian等[14]基于最小化位移方差方法,对白噪声激励下的无阻尼单自由度TMDI结构系统进行数值优化;Pietrosanti等[15]针对多自由度-TMDI结构系统,通过频率分析,研究了在高斯零均值白噪声随机激励下结构体系模态参数优化问题;李超等[16]基于遗传算法,对加速度激励下的调谐黏滞质量阻尼器TVMD进行了参数优化研究。
此外,定点理论作为阻尼器参数优化的另一重要方法,由Den Hartog于1985年首次提出[17]。该方法基于主结构频响曲线特性,通过韦达定理得到阻尼器在简谐激励下的最优参数解析解表达式。董飞等[18]采用修订的定点理论研究夹层阻尼悬臂式TMD相互耦合时动力参数之间的变化规律,提出解耦的两阶段设计方法;李亚峰等[19]提出一种新型减振装置即惯质调谐质量阻尼器VTMDI,并采用定点理论对其减振性能进行系统研究;Ikago等[20]基于惯容系统提出调谐黏滞质量阻尼器(TVMD),并采用定点理论优化其参数;罗浩等[21]采用定点理论研究串联黏性质量阻尼器SVMD的优化参数,得出SVMD的结构响应传递函数。
输电导线微风振动是一种涡激振动。当微风吹过导线时,在其截面上下侧依次形成涡旋,这种规律性涡旋会在截面上下侧交替产生垂直于来流方向的横风向作用力,由此形成振动响应。为了抑制此类振动,本文基于定点理论,研究了谐波荷载作用下TMDI振动控制机理,旨在为输电导线微风振动防治措施研究提供理论基础。
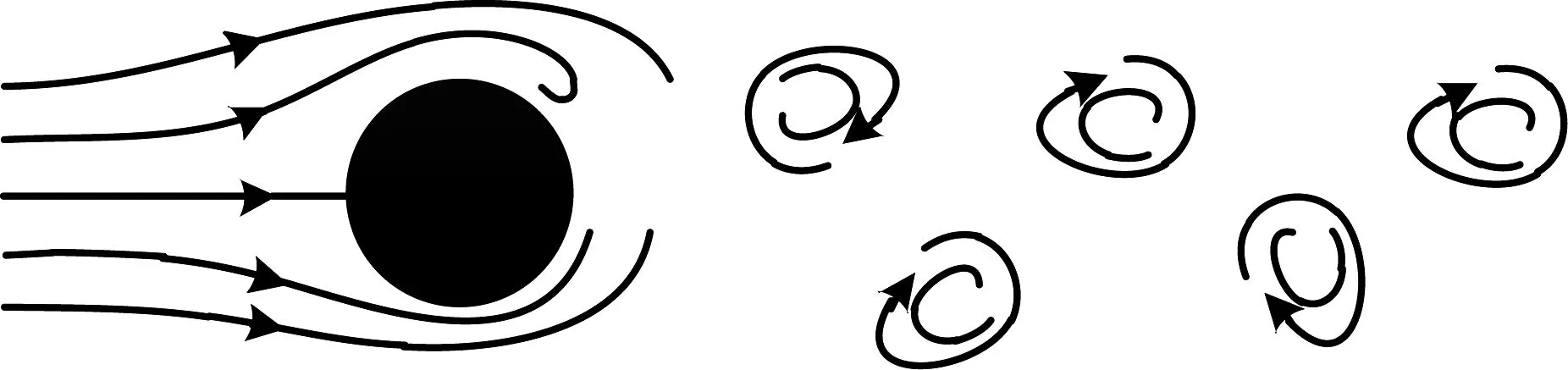
图1 旋涡脱落引起的微风振动Fig.1 The vibration of a breeze caused by vortex shedding
1 惯质调谐质量阻尼器振动控制机理研究
1.1 理想系统模型
早在21世纪初Smith提出惯容系统[22],由于其特殊的结构形式,最初主要用于高性能车辆悬架系统的振动控制[23-25]。随着研究的深入,TMDI现已被广泛用于建筑[26-28]、桥梁[29]、风力涡轮机[30-31]的抑振耗能中。
理想惯容系统是一种具有独立自由度的线性装置,节点间产生与其相对加速度成正比的反作用力,见式(1)[32]
(1)
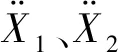
常见的惯容系统形式主要有齿轮齿条、滚珠丝杠[34]以及液压式[35-36],各种形式的惯容器,如图2所示。
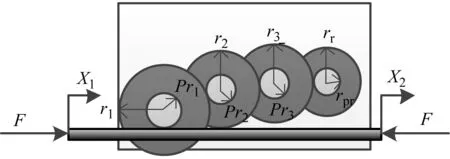
(a) 齿轮齿条式
齿轮齿条型惯容系统通过齿轮齿条将平动动能转换为转动动能,以改善传统TMD减振性能。这类惯容系统的振动控制效率与齿轮数量及传动比有关,其中表观质量b计算公式[37]如式(2)所示
(2)
式中:mf为实心飞轮质量;rr、rpr为实心飞轮旋转半径及其对应小齿轮半径;rk、prk(k=1,2,3)为第k个大齿轮半径及其对应小齿轮的半径。
此外,惯容系统与TMD的连接方式对结构振动控制效率也有一定影响。通过惯容系统将TMD与主结构相连,称为非接地TMDI;惯容系统一端接地,另一端与TMD相连,称为接地TMDI;两种连接方式如图3所示。
1.2 单自由度结构体系运动方程及最优参数解析解
1.2.1 非接地惯质调谐质量阻尼器
对于非接地结构体系(图3(a)),动力学方程表达式如下
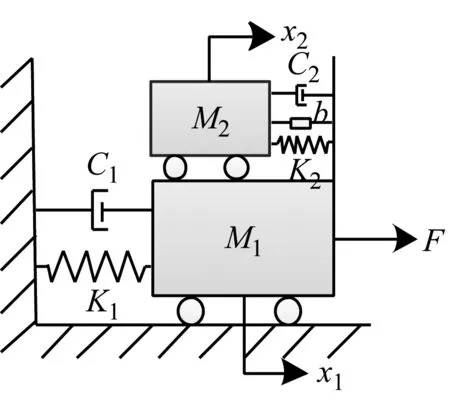
(a) 非接地TMDI
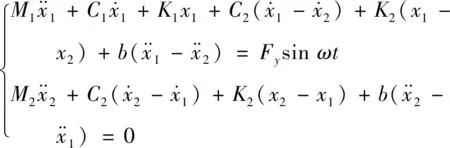
(3)
式中:M1、K1、C1为主结构的质量、刚度和阻尼;M2、K2、C2为TMDI的质量、刚度和阻尼;x1、x2为主结构、TMDI的横向位移。
对附加非接地TMDI的主结构,设施加的简谐激励力为
F=Fyeiωt
(4)
主结构与非接地TMDI的位移分别表示为
x1=X1eiωt,x2=X2eiωt
(5)
式中,X1、X2为x1、x2的复数振幅。
则主结构与非接地TMDI的速度与加速度分别表示为
(6)
将式(4)~式(6)代入式(3)可得主结构响应振幅
(7)
主结构受外界激励作用的幅值表示为Xst=Fy/K1,则结构体系振动的动位移与静位移之比即动力放大系数(DMF)表示为
(8)
其中
R1=K2-bω2-M2ω2
R2=C2ω
R3=K1K2-(C1C2+bK1+M1K2+M2K1+M2K2)ω2+(bM1+bM2+M1M2)ω4
R4=(C2K1+C1K2)ω-(bC1+C2M1+C1M2+
C2M2)ω3
(9)
根据定点理论,忽略主结构阻尼的系统频响曲线均经过固定点P、Q。当固定点高度相等且达到最大值时,减振效率最高,如图4所示。
Den Hartog对比研究了主结构阻尼对TMD系统的振动控制效率的影响,得到结论:定点理论可用于小阻尼结构(阻尼比5%以内)的振动优化研究[38]。因此本文采用定点理论,以主系统无阻尼附加非接地和接地TMDI系统为对象推导最优参数解析解。
定点理论中动力放大系数一般化表达式为
(10)

图4 定点理论Fig.4 The fixed point theory
为了明确参数A-G,引入如下规定
(11)
式中:ω1、ω2为主结构和TMDI的固有频率;ζ1、ζ2为主结构和TMDI的阻尼比;μ为TMDI质量与主结构质量之比;β为表观质量与TMDI质量之比;λ为外激励力与主结构的频率比;γ为TMDI与主结构的频率比。
将式(11)代入式(8),整理得到无阻尼主结构-非接地TMDI动力放大系数如下
(12)
观察式(10)、(12)可知
(13)
为了确定最优频率比,通过定点理论可知,ζ2的变化对固定点P、Q的取值均无影响,故整理式(10)如下
(14)
忽略ζ2对固定点P、Q的取值影响,故还需满足以下关系
(15)
考虑两者的极性相反,式(15)可简化为
(16)
整理得
(17)
设求解结果为λP、λQ,根据韦达定理可得
(18)
此时,忽略ζ2的动力放大系数为
(19)
根据定点理论,最优频率比条件下λP、λQ两点的动力放大系数相等,即
(20)
则
(21)
联立式(18)、(21),求解可得
2EAG=D(BF+D-EC)
(22)
将式(13)参数A~G代入式(22),最优频率比为
(23)
通过韦达定理,可得固定点P、Q横坐标λP、λQ
(24)
将参数A~F代入到式(24)中可得
(25)
固定点P、Q为频响曲线最高点时,减振效果最优。故对式(10)求极值,得到结构最优阻尼比表达式
(26)
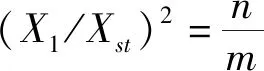
(27)
其解按照ζ2多项式进行整理可得
(28)
式中,参数I4、I2、I0为
I4=-2D2G2λ6+2DEG2λ4
I2=(3A2G2+C2D2)λ8-(4CD2+4ABG2)λ6+(B2G2+4CDE+3D2+2AG2-C2E2)λ4-(4DE)λ2+(E2-G2)
I0=(-2A2C2)λ10+(2ABC2+6A2C)λ8-(4A2+8ABC)λ6+(6AB+4AC+2B2C-2BC2)λ4-
(4A+2B2-2C2)λ2-(2B-2C)
(29)
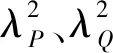
(30)
选择任一阻尼比值时,仅能满足P、Q其中一点为结构频率响应曲线极值,故取其平均值作为最优阻尼比,即
(31)
将参数A~F代入上式,可得最优阻尼比
(32)
此时,最大动力放大系数为
(33)
1.2.2 接地惯质调谐质量阻尼器
对于接地结构体系(图3b),其动力学方程表达式如下

(34)
可得主结构位移为
(35)
化简上式可得无阻尼主结构-接地TMDI的动力放大系数
(36)
观察式(10)、(34),可得各个参数
(37)
将各参数代入式(22),即可得
(38)
取其正值并化简,得其最优频率比
(39)
将参数A~G代入式(24)中可得固定点P、Q横坐标λP、λQ
(40)
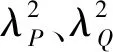
(41)
此时,最大动力放大系数为
(42)
2 结构振动响应分析
表1总结了两种连接方式TMDI及传统TMD的参数解析解。通过表1结果,图5~图8表示表观质量比为0~0.6时调谐参数随质量比变化的函数曲线,并讨论了调谐参数对主结构-TMDI振动特性的影响。

表1 减振系统的优化解析解Tab.1 Optimal analytical solution of vibration reduction system
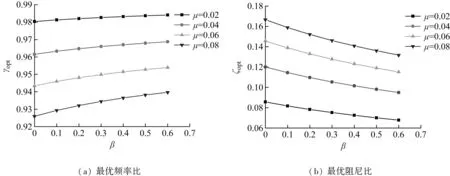
图5 非接地TMDI最优设计参数Fig.5 Optimal design parameters for unground TMDI
由图5可知,随着表观质量比β增加,最优频率比γopt线性增加,最优阻尼比ζ2opt线性减少。反之,随着质量比μ的增加,γopt线性减小、ζ2opt线性增大。
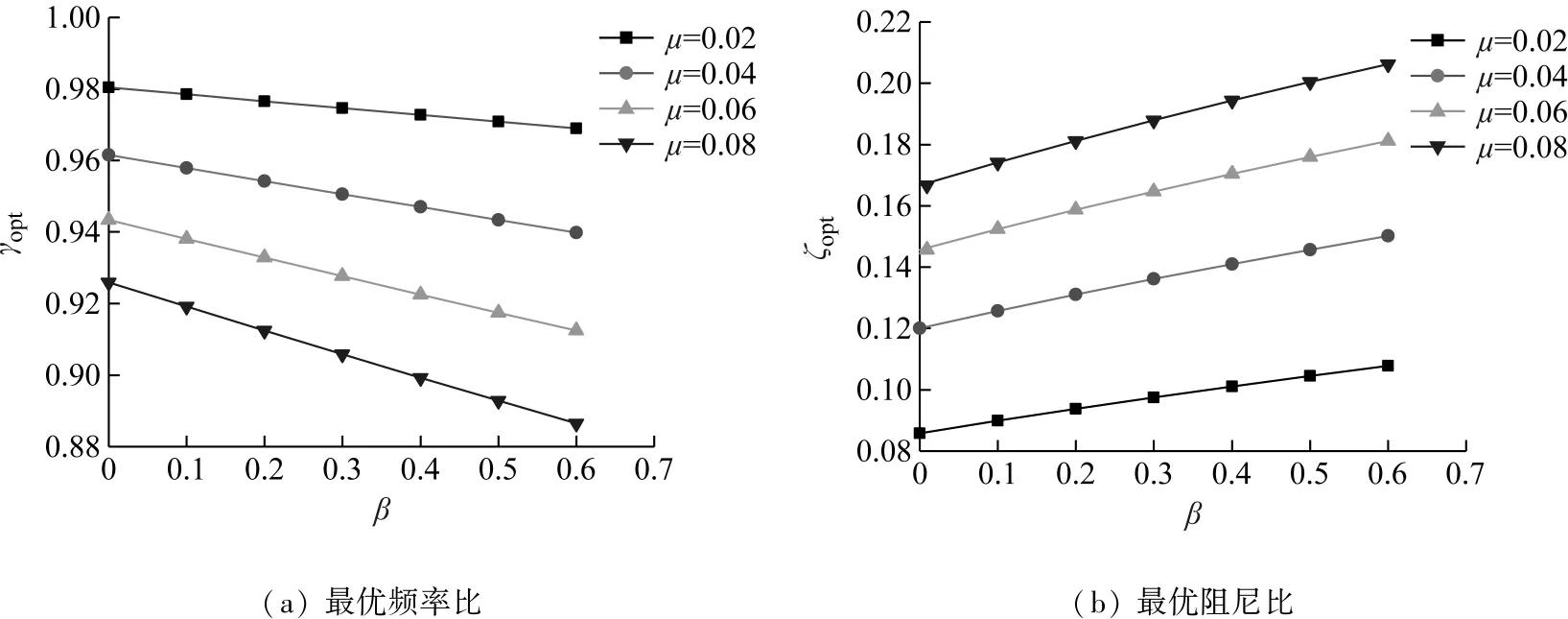
图6 接地TMDI最优设计参数Fig.6 Optimal design parameters for ground TMDI
由图6可知,随着表观质量比β的增加,γopt线性减小,ζ2opt线性增加。随着质量比μ的增加,γopt线性减小、ζ2opt线性增大。

图7 最优动力放大系数Fig.7 Optimal dynamic amplification factor
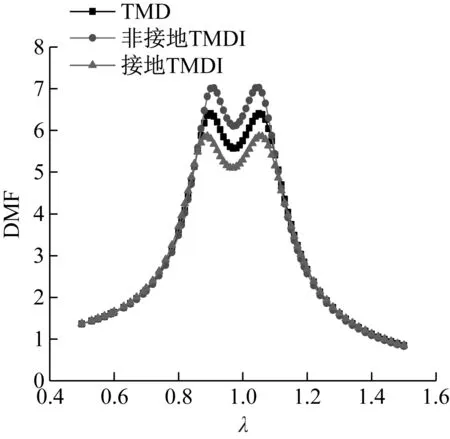
图8 主结构频率响应曲线比较Fig.8 Comparison of frequence response curves of the primary structure
由图7可知,非接地TMDI的动力放大系数随着表观质量比β的增大而增大。由表1可知,当β=0时,结构体系为TMD,此时结构动力放大系数小于非接地TMDI。结果表明非接地惯容系统降低了TMD的减震效率,在一定程度上隔断了能量传递,从而无法实现有效耗能。
对于接地TMDI,结构动力放大系数随表观质量比β增大而减小,表明该类连接形式有助于提高结构体系减振效果,改善TMD系统的耗能效率。
此外,无论采用何种连接形式,TMDI的动力放大系数均随着质量比μ的增加而减小。但为了减轻附加质量对结构承载能力的不利影响,故在结构振动控制过程中,通常限制质量比μ在0.2以下。
当μ=0.05,β=0.2时,根据表1得到最优频率比及最优阻尼比如下
TMD:γopt=0.952、ζ2opt=0.134;
非接地TMDI:γopt=0.956、ζ2opt=0.956;
接地TMDI:γopt=0.943、ζ2opt=0.146。
根据上述的最优参数得到激励频率λ与动力放大系数DMF的关系曲线,如图8所示。与传统TMD和非接地TMDI相比,接地TMDI的峰值动力放大系数下降约8.4%、16.5%。结果表明,接地TMDI能有效控制主结构振动,而非接地TMDI对结构振动控制不利。由此可见惯容系统连接位置对TMD吸振能力影响显著。
3 结构鲁棒性分析
为了研究阻尼器受主结构固有频率及自身阻尼摄动对振动控制效率的影响,本节从ω1和C2发生摄动分别进行研究。
3.1 主结构频率摄动
由于结构刚度与模态频率成比例,本节将通过结构刚度的等比变化,研究结构固有频率摄动对TMDI鲁棒性的影响。由图9可知,以最优刚度曲线为基准,随着刚度的减小,曲线峰值偏左。反之,曲线峰值偏右。此外,刚度的变化均会使得曲线由双峰向单峰转变,且单峰峰值大于双峰。

图9 主结构刚度变化后的响应曲线Fig.9 Response curve of main structure after stiffness change
图10所示为三种减振方式下,主结构动力放大系数随刚度摄动的变化规律。与其他两种振动控制方式相比,接地TMDI能够很好的维持控制效果。且由图8可得,接地TMDI调频宽度增大约6%、13%。
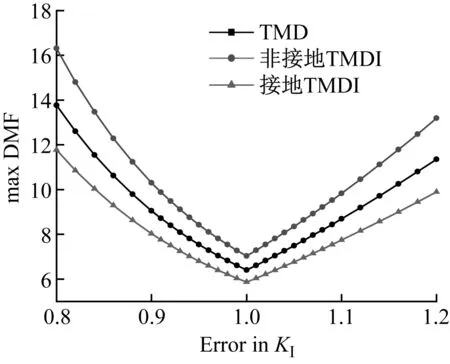
图10 主结构刚度等倍变化后三种阻尼器的比较Fig.10 Comparison of three kinds of shock absorbers after main structure stiffness change
3.2 阻尼器阻尼摄动
如图11所示,在0.2ζ2opt~2ζ2opt变化范围内,以1.0ζ2opt曲线为基准,主结构响应曲线峰值均有所上升。当摄动范围在0.2ζ2opt时,相对于接地TMDI,非接地TMDI系统响应峰值大幅增加,由此可得非接地TMDI受阻尼摄动影响较大。
如图12所示,在摄动范围内,主结构动力放大系数变化平缓,仅为最小动力放大系数的1.5倍。且与传统TMD和非接地TMDI相比,接地TMDI动力放大系数减少约0.6%、1.6%。结果表明:较其他两种减振装置,接地TMDI吸振能力受阻尼摄动影响最小总体而言,对于主结构频率和阻尼系数的摄动,接地TMDI的鲁棒性更为优秀。
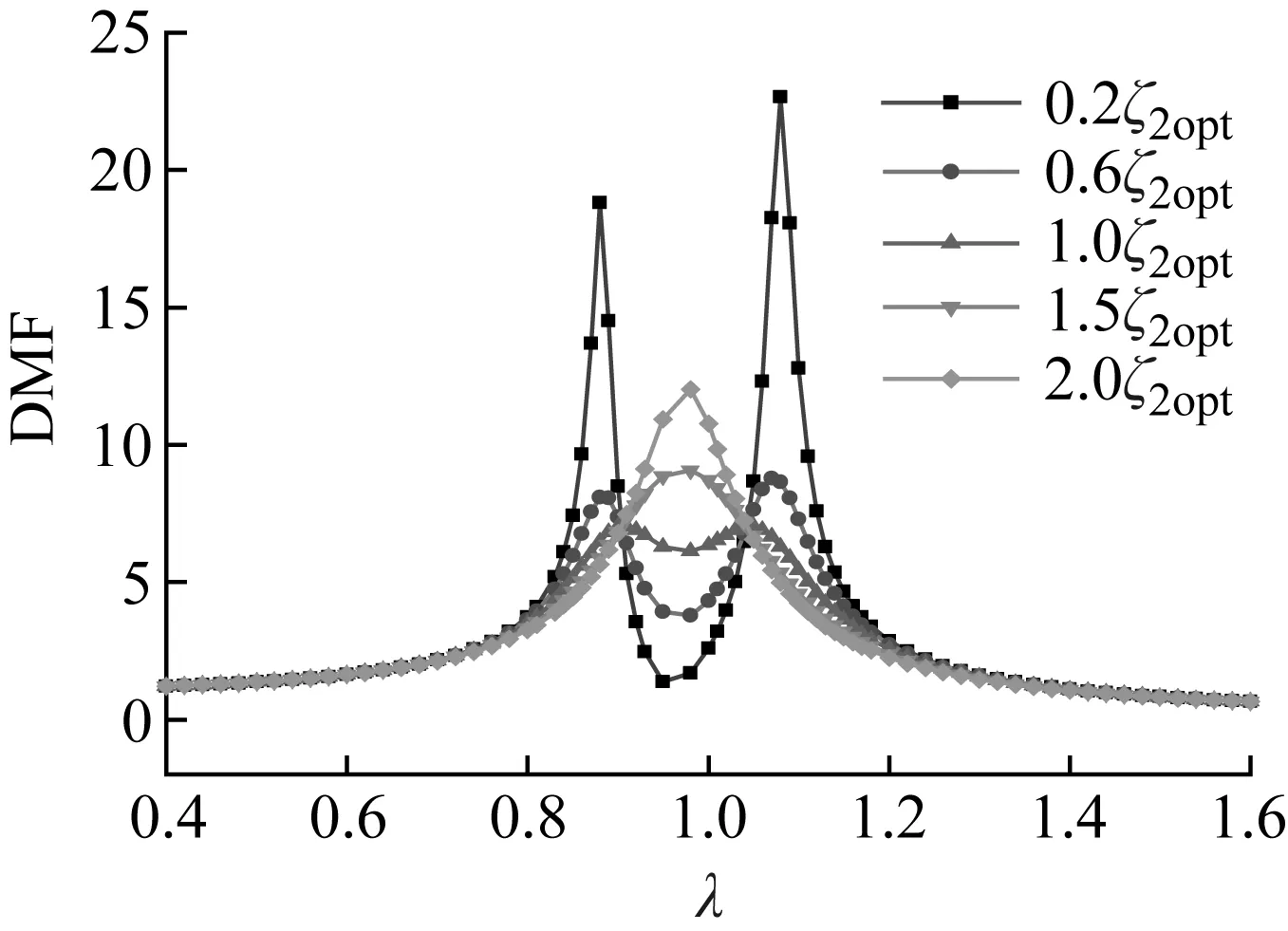
(a) 非接地TMDI
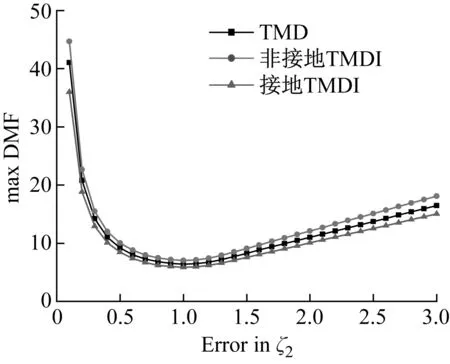
图12 阻尼比等倍变化后三种阻尼器的比较Fig.12 Comparison of three kinds of shock absorbers after damping coefficient change
4 结 论
本文通过单自由度主结构附加TMDI系统模型建立动力学方程,对结构参数进行了详细的研究,并分析对比TMD、非接地和接地TMDI在主结构受简谐激励力下的减振性能和鲁棒性,得出以下主要结论:
(1) 采用定点理论推导出激励力下TMDI的最优频率比和最优阻尼比的解析表达式。
(2) 相同条件下接地TMDI与传统TMD相比动力放大系数下降约8.4%,与非接地TMDI相比下动力放大系数下降约16.5%,接地形式的TMDI减振效果更显著。
(3) 当主结构刚度发生摄动时,接地TMDI调频宽度相比传统TMD提高约6%,与非接地TMDI相比提高约13%。在阻尼器的阻尼比摄动范围内,接地TMDI减振系统动力放大系数增幅仅约1.5倍,接地TMDI吸振能力受阻尼比摄动影响最小。故接地TMDI的鲁棒性明显优于TMD和非接地TMDI。
