结合标签集语义结构的多标签特征选择算法
2023-01-31潘敏澜孙占全王朝立曹高宇
潘敏澜,孙占全,王朝立,曹高宇
(上海理工大学 光电信息与计算机工程学院,上海 200093)
1 引 言
多标签学习作为机器学习的一个分支,应用广泛,例如在文本分类[1]、图像自动标注[2]、基因分析[3]等领域有着广泛的应用.
随着科学技术的迅速发展,数据维度变高,给多标签学习带来巨大的挑战,研究学者们称之为维度灾难[4].维度灾难主要表现为以下两个方面:首先,高维度数据会给多标签学习增加巨大的计算代价[5].其次,高维数据会带来大量无关或冗余信息,多标签分类器在训练中大量拟合无关和冗余信息,使得泛化性能和预测精度降低[5].
多标签特征选择作为一种降维技术,能有效解决上述的维度灾难问题.特征选择能筛选出和学习问题相关的信息,剔除无关和冗余信息,达到提升分类器性能和减少计算代价的目的.多标签特征选择算法分为3大类:袋装式、嵌入式、过滤式.袋装式算法筛选特征需要根据特定的分类器,每筛选一次特征都需要重新训练一次分类器,优点是能考虑到特征组合的多样性,缺点在于计算量非常大.由于实际上特征之间组合数非常浩大,故一般袋装式算法会结合启发式算法,如张敏灵等人提出的MLNB[6].嵌入式算法则和分类器融为一体,即它本身就是分类器.一般嵌入式算法结合凸优化、正则化等方法得到权重矩阵来判别各特征的重要性,如JFSC[7]、SFUS[8].过滤式算法独立于分类器,通常结合信息论指标如互信息[9,10]、模糊互信息[11]、交互信息[12]、近邻粒度[13]、统计学指标余弦相关性和皮尔逊相关系数[14]、多标签代价敏感策略[15],来评价特征的重要性.一般认为,过滤式算法计算简便,灵活高效.
本文将结合互信息衡量标签和标签的相关性,再通过标签集的聚类结合最大相关最小冗余框架筛选特征.
2 理论基础
2.1 信息熵
定义 1.熵(entropy)最早由香农提出[16],在信息学,热力学,社会科学等领域有着广泛的应用.信息熵是衡量一个变量所携带的信息.在给定随机变量X={x1,x2,…,xn},熵的定义如下:
(1)
其中p(xi)表示变量xi出现的概率.
定义 2.二维联合熵衡量两个随机变量一起包含的信息,给定随机变量X={x1x2,…,xn},Y={y1,y2,…,ym},二维联合熵的定义如下:
(2)
其中p(xi,yj)表示变量xi,yj的联合概率.
定义 3.类似的定义可以扩展到高维熵:
H(X1,X2,…,Xn)
(3)
其中p(xi1,xi2,…,xik)是联合概率.
定义 4.条件熵衡量在一个变量被观察到的情况下,另一个变量单独包含的信息.给定随机变量X={x1,x2,…,xn},Y={y1,y2,…,ym},它的定义为:
(4)
其中p(xi,yj)和p(xi|yj)分别表示变量xi,yj的联合概率.
性质 1.联合熵、条件熵、熵之间的关系:
H(X,Y)=H(Y)+H(X|Y)
(5)
2.2 互信息
定义 5.互信息衡量两个变量共同的信息.给定随机变量X={x1,x2,…,xn},Y={y1,y2,…,ym},互信息的定义如下:
(6)
性质 2.互信息、熵、联合熵之间的关系:
I(X,Y)=H(X)+H(Y)-H(X,Y)
(7)
定义 6.条件互信息衡量在给定一个随机变量,另外两个随机变量共同包含的信息,它的定义如下:
I(X;Y|Z)=H(X|Z)-H(X|Y,Z)
(8)
定义 7.交互信息衡量3个变量之间的信息协同和冗余程度.当交互信息为正时表明,3个变量的信息含有冗余,当交互信息为负时表明3个变量信息具有协同作用.给定随机变量X,Y,Z,交互信息定义如下:
I(X;Y;Z)=I(X;Y)-I(X;Y|Z)
(9)
性质 3.交互信息具有对称性:
I(X;Y;Z)=I(X;Z;Y)=I(Y;X;Z)
(10)
3 相关工作
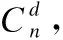
J(f+)=I(S,f+;L)-I(S;L)
(11)
其中f+∈F-S,S是已选择的特征集合,L是标签集.
根据公式(3)和公式(6),可知公式(11)涉及高维熵和高维概率的计算,计算量极大.因此这现年学者大多从高维互信息或高维熵的近似估计的角度入手.
2012年,Lee和Kim提出AMI[17](Approximating mutual information)算法.该算法规避无法精确计算高维联合互信息的问题,提出基于Shearer′s inequality[18]的高维互信息近似算法.该算法选择特征通过最小化如下指标:
(12)
从整体上该算法未能体现多标签的数据的特性,即未考虑标签与标签之间的相关性.2013年Lee和Kim提出了考虑成对标签相关性的特征选择算法PMU[19](Pairwise Multi-label Utility),该算法选择特征最大化如下指标:
(13)
该算法解决了标签相关性的问题,但涉及大量的交互信息计算,因此计算量极大.
2015年,Lee和Kim改进了PMU计算量大的问题,提出D2F[20]算法.和PMU算法相比D2F少了第3项,具体选择特征最大化如下指标:
(14)
同年,林耀进等人受单标签特征选择算法MRMR[21](Max-Relevance and Min-Redundancy)的启发,在多标签领域提出MDMR[22]算法,该算法选择特征最大化如下指标:
(15)
2017年,Lee和Kim在最大相关和最小冗余的框架下,提出基于两者可伸缩的系数特征选择算法SCLS[23].该算法有效解决因标签集过大而导致的评估误差问题,该算法选择特征最大化如下指标:
(16)
2019年,张萍等人提出基于标签冗余的算法LRFS[24].该算法,针对两种特定的标签类型,基于标签和标签之间的冗余来度量特征和标签的相关性.
在其他方向的多标签特征选择领域中,如2020年孙林等人基于ReliefF提出名为RFNMIFS[25]的多标签特征选择算法.同年Mohsen Paniri等人第一次在多标签特征选择应用蚁群算法(ACO)提出MLACO[14]算法,该算法结合皮尔逊相关性系数和余弦相关性系数构造信息素和启发因子筛选特征.
综上所述,以上基于互信息的算法缺乏考虑标签集的结构,如MDMR,LRFS,PMU,D2F都只考虑到二阶标签相关性,没有考虑标签集的高阶相关性和语义结构.本文基于互信息和标签集的聚类,提出同时兼顾标签集高阶相关性和语义结构的多标签特征选择算法.
4 所提方法
4.1 标签集聚类
标签集自身是带有语义结构的.例如假设一个自然景色的数据集有蓝鲸、骆驼、仙人掌、海浪、森林、猴子、海鸥这7个标签.显然自然风景中,蓝鲸和骆驼很难出现在一个样本里,这两个标签基本是互斥的.实际上,这7个标签很容易得到一个语义结构:蓝鲸、海鸥、海浪为一组,代表海洋风景,森林和猴子为一组,代表森林风景,仙人掌和骆驼为一组,代表沙漠风景.传统算法大多只考虑二阶标签相关性而忽略二阶以上的相关性,从而忽略标签集固有的语义结构.针对传统算法的不足,本文应用标签聚类获得标签集语义结构.即将蓝鲸、海鸥、海浪聚为一类,森林和猴子聚为一类,仙人掌和骆驼聚为一类.
我们先构造标签相关性矩阵.假设训练集的标签集为:L={l1,l2,…,lq}.我们依据标签两两之间的互信息给出标签的相关性矩阵:
定义 8.互信息矩阵T:
T=(tij)q×q
(17)
若li≠lj,则tij代表标签li和标签lj的互信息,若li=lj,则tij=0.也即:
(18)
显然T是对称阵,主对角线元素均为0,即标签自身和自身的相关性不计入统计.为了防止标签熵的差异导致互信息相差过大这里我们引入互信息与标签熵权重占比的相关性矩阵,为了下文叙述方便,我们将称之为互信息权重占比矩阵:
定义 9.互信息权重占比矩阵R:
R=(rij)q×q
(19)
其中
(20)
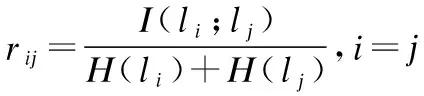
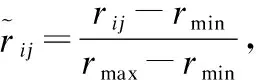
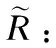
(21)
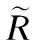
下面通过一个例子来说明标签的聚类.给定一个人工训练集数据标签集示例,具体如表1所示.
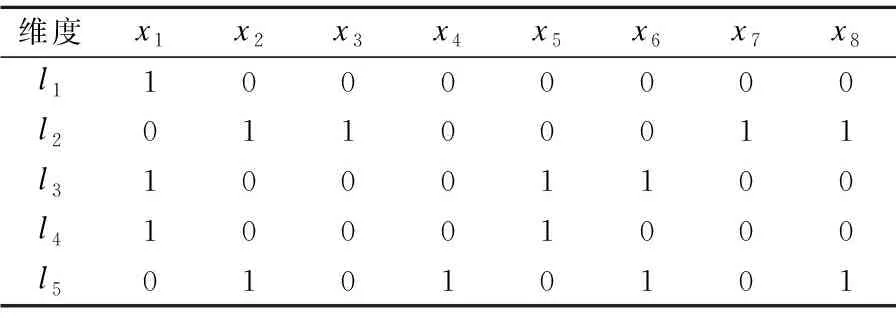
表1 人工训练集数据标签集示例Table 1 Artificial training data tag set example
第1步,基于上面的数据,根据(6)式计算出互信息矩阵T(式(6)中的对数我们以自然常数为底,取值保留4位小数,若为0则不计后4位小数):
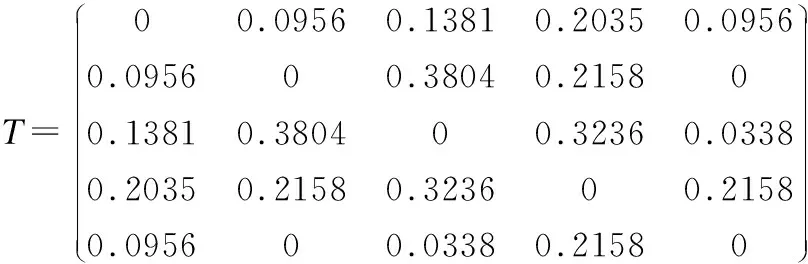
(22)
第2步,按照定义9计算矩阵R:

(23)
可以看到,R中的取值集中在0到0.3之间.
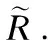

(24)
最终得到结果:聚类向量[0 0 0 1 0],即标签l1、l2、l3、l5为一类,l4为一类.
4.2 特征选择
应用AP算法得到了标签聚类簇记为C1,C2,…,Ck共k共个簇.其中,∀Ci⊆L,包含ji个标签,即Ci={li1,li2,…,liji}.
为了分析方便,考虑标签只有7个的情况,我们结合信息韦恩图来分析,原始标签集的信息韦恩图如图1所示.
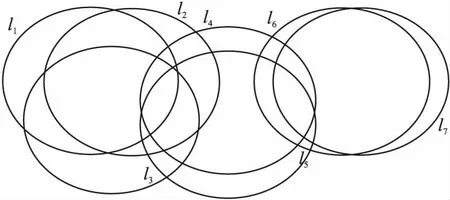
图1 7个标签的信息韦恩图Fig.1 Information Venn diagram of 7 labels
聚类后的示意图如图2所示.
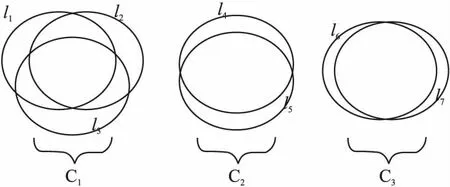
图2 聚类后的信息韦恩图Fig.2 Information Venn diagram after clustering
传统的方式衡量相关项大多对标签无差别对待,没有挖掘标签语义结构信息.通过聚类把强相关性的标签归为一簇,彼此弱相关的标签分离开.不同于标签传统的相关性衡量式(25),我们采用式(26)的近似方式.
Rel(f)=I(f;L)≈∑l∈LI(f;l)
(25)
Rel(f)=I(f;L)≈∑Ci⊆LI(f;Ci)
(26)
由于同簇中的标签相关性很强,以遍历的方式累加则会造成互信息重复计算.以簇3为例说明,假定特征f与簇3的信息韦恩图如图3所示.

图3 特征f与簇C3信息韦恩图Fig.3 Information Venn diagram of feature f and cluster C3
当出现如图3所示的情况时,特征与l6,l7正确的相关性度量即互信息为:I(f;C3)=b+c.而传统的遍历累加方式为I(f;C3)=b+c+c,因此单从簇C3上的相关性度量上看,传统的遍历累加方式会多计算一遍c区域,因此传统的方式会在相关性度量时造成巨大的误差,从而影响算法的性能.
针对以上传统方法的不足本文提出以下特征与簇相关性的近似估计方法.给定∀Ci⊆L,我们采用新的相关性估计,簇Ci与特征的相关性为:
(27)
应用式(27)验证图3中的情况,I(f;C3)=maxI(f;l6),I(f;l7)=I(f;l6)=b+c,和真实的值b+c相同.
扩展到整个标签集根据式(26),式(27),可得到特征和标签集的相关性:
(28)
应用最大相关最小冗余框架可得到筛选特征指标:
J(f)=Rel(f)-Red(f)
(29)
其中Rel(f)根据式(28)计算.Red(f)代表特征f和已选特征子集的冗余,Red(f)的计算如式(30)所示:
(30)
其中S是已选特征子集.
由于算法前向式搜索在筛选特征过程中,已选特征子集数量是逐渐增长的,因此需要乘上一个平衡项,防止冗余项和相关项因簇的个数和已选特征子集的个数不平衡导致其中某一项的误差被放大.结合式(29)得到最终的指标如式(31)所示:
(31)
其中k为AP聚类算法得到的聚类个数,|S|代表已选特征子集的个数.
本文所提算法的描述如算法1所示.
算法1.
输入:训练集标签原始特征F={f1,f2,…,fn},训练集标签集L={l1,l2,…,lq},需要选择的特征数d.
输出:特征子集S.
Begin:
3.初始化S→Ø;
4.选择第一个特征:使得∑l∈LI(f;l)最大的f;
与S:
5.更新F,F→F-f;
6.更新S,S→S+f;
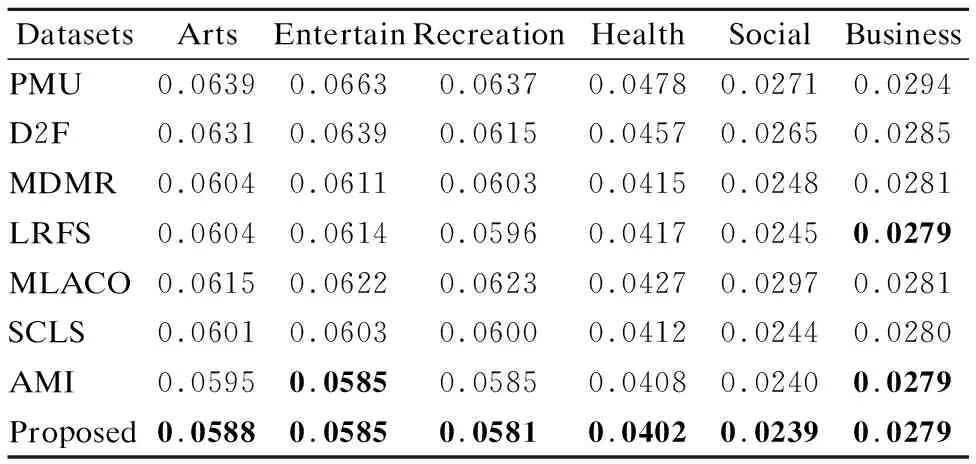
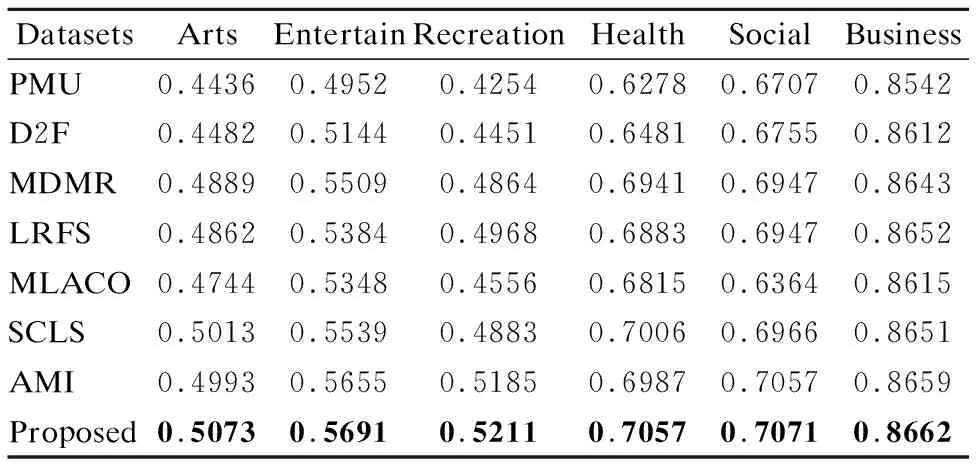
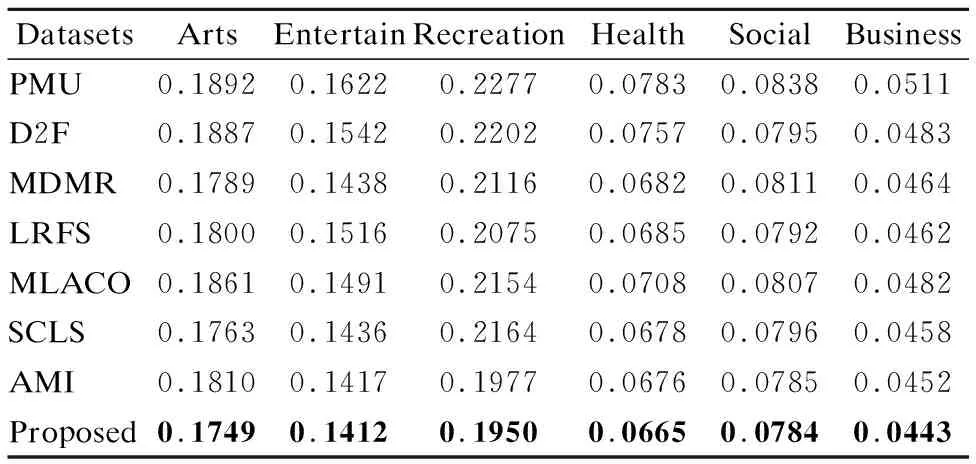
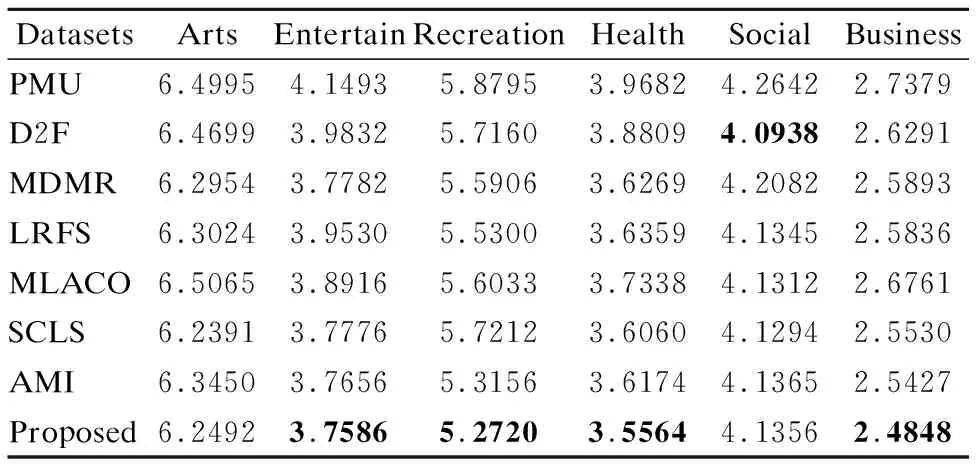
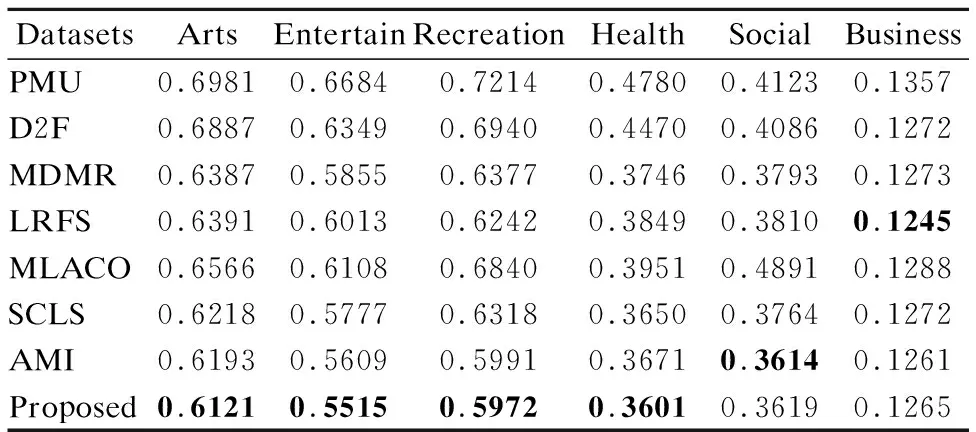
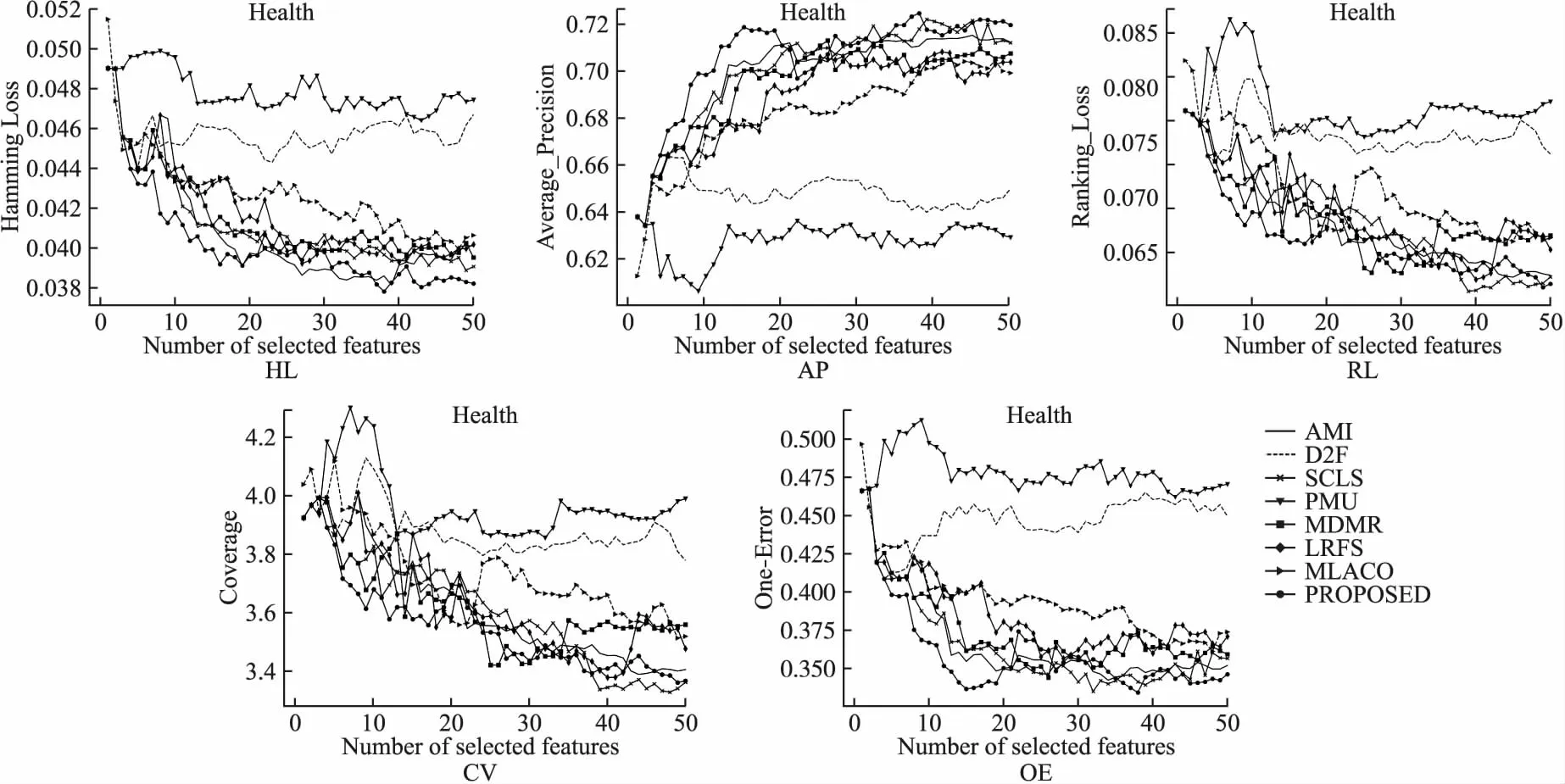
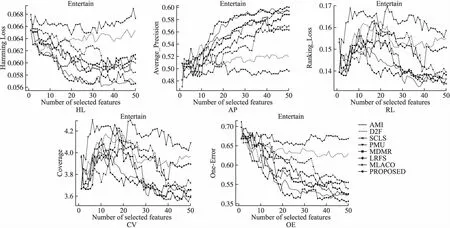
7. while |S| 8. For infiinF; 9. 根据式(31)计算J(fi); 10. 记录7)中使得J(·)最大的特征fj; 11. 更新F,F→F-fj; 12. 更新S,S→S+fj; 13. end while; 14.返回特征子集S End 假定数据集样本个数为m,特征个数为d,需要选择的特征个数为b,标签个数为q.本算法分为两部分.第1部分聚类算法时间复杂度为:O(mq2).第2部分计算指标的算法时间复杂度为:O(mdq)+O(mdb).故本文算法时间复杂度为:O(mq2+mdq+mdb). 本文实验数据为6个真实多标签数据集:Arts、Entertain、Recreation、Health、Social、Business.以上数据集均来源于Mulan Library[27].各数据集详细信息如表2所示. 表2 多标签数据集Table 2 Multi label datasets 为了对比算法的性能,本文采用了汉明损失(Hamming Loss),平均精度(Average Precision),排序损失(Ranking Loss),覆盖率(Coverage),0-1损失(One Error)5个评价指标[28],为了方便展示,5个评价指标分别记为HL(↓)、AP(↑)、RL(↓)、 CV(↓)、 OE(↓).其中有标↑记号的表示数值越大算法性能越好,标↓记号的表示数值越小算法性能越好. 本文选取近些年来著名的算法作为对比.分别为PMU[19]、D2F[20]、MDMR[22]、SCLS[23]、AMI[17]、LRFS[24]、MLACO[14].6个数据集均选择50个特征,步长为1,每选一个特征就将所选的特征加入已选特征子集作为分类器的输入.由于6个数据集特征数值是连续的,本文所提算法采取3等宽离散方式. 此外,分类器均用MLKNN[29]平滑系数设为1,近邻系数k设为10. 实验结果如表3-表7所示.其中每一个指标的数值,是50次结果的平均值,结果保留4位小数.表中黑体字代表同一个数据集上,该指标最优的结果.此外“Proposed”代表本文所提算法. 表3 所有算法在HL(↓)指标下的结果Table 3 Results of all algorithms under HL(↓)index are compared 从表3-表7的结果上,不难发现本文所提算法在6个数据上的结果是最优的. 在指标HL上,如表3所示.本文算法在6个数据集上均取得最好的结果.其中在Entertain数据集上,本文算法的性能和AMI算法并列排名第一,在Business数据集上,本文算法的性能和LRFS以及AMI算法并列排名第一. 在指标AP上,如表4所示.本文算法在6个数据集上均取得最好的结果. 在指标RL上,如表5所示.本文算法在6个数据集上均取得最好的结果. 表4 所有算法在AP(↑)指标下的结果Table 4 Results of all algorithms under AP(↑)index are compared 表5 各算法在RL(↓)指标下的结果Table 5 Results of all algorithms under RL(↓)index are compared 表6 所有算法在CV(↓)指标下的结果Table 6 Results of all algorithms under CV(↓)index are compared 在指标CV上,如表6所示.本文算法在Entertain,Recreation,Health,Business数据集上取得最好结果. 在指标OE上,如表7所示.本文算法在Arts、 Entertain、Recreation、Health数据集上取得最好结果. 表7 所有算法在OE(↓)指标下的结果Table 7 Results of all algorithms under OE(↓)index are compared 从整体上看,本文算法在HL、AP、RL、CV、OE指标上最优率分别为100%,100%,100%,66.7%,66.7%,平均最优率在86.7%,因此可以证明本文算法有很强的鲁棒性和有效性. 为了展示更多的细节,本文给出了Health和Entertain两个数据集上的各指标趋势图,如图4-图5所示.其中横坐标为选择特征的个数,纵坐标是个指标的数值. 以数据集Health中HL指标为例.图4中,从Health数据集上的HL指标趋势图上,可以看到本文算法的大部分情况都是最优的.此外,在选择特征数为1-20时,本文算法明显优于其余算法,因此在特征选择的简约性上也明显占优.其他四个指标上,本文算法同样是最优的. 图4 Health数据集上各指标的趋势图Fig.4 Trend chart of each indicator on the Health data set 传统的算法如PMU和D2F由于指标中含有交互信息,累加过程中项数过多,导致误差累积的越来越大,因此算法效果不佳.筛选特征指标中含有交互信息项的算法MDMR和LRFS同样存在类似的缺陷,因此在性能上都未能取得最优.MLACO的算法由于是基于余弦相关性和皮尔逊相关系数两种线性相关性构建筛选特征指标,因此对非线性相关性挖掘不够,因此性能上也未能达到最优.AMI和SCLS算法筛选特征是基于互信息的,忽略了标签和标签之间的相关信息,因此性能同样未达到最优. 图5 Entertain数据集上各指标的趋势图Fig.5 Trend chart of each indicator on the Entertain data set 本文基于互信息和相关性聚类思想,提出了基于标签语义结构的特征选择算法.克服了传统算法相关性度量通过累加形式导致忽略标签相关性或只考虑两两标签相关,以及引入交互信息增加计算量的缺点.本文算法和近几年的7种算法在6个数据集上进行对比实验.每个数据集上均用5个指标作为结果对比.实验结果表明本文算法具有明显优势.尽管在这6个数据集上有着较好的表现.但对于标签个数较少的数据集采用聚类方法可能导致效果不佳.因此在未来,我们着重探索其他相关性分析方法,挖掘标签集的语义结构,从而提出更加精准的特征选择指标.5 实验设计与分析
5.1 实验数据
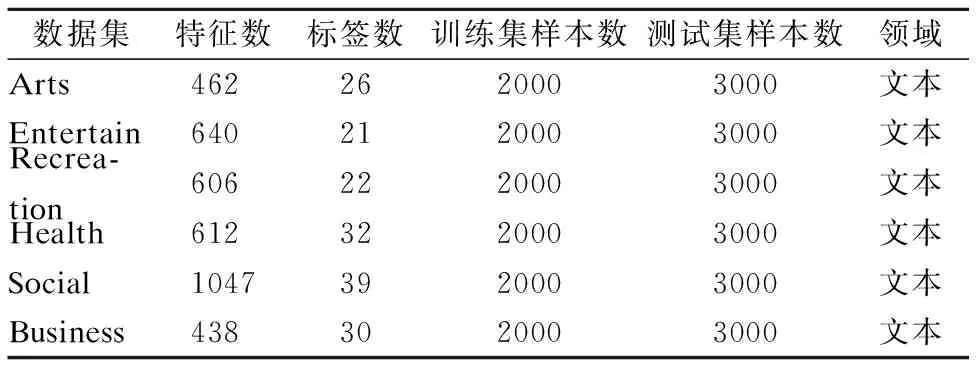
5.2 评价指标
5.3 实验设计及结果分析
6 结束语
