融合孤立森林和局部离群因子的离群点检测方法

凌 莉 程张玉 邹承明

1(武汉工程职业技术学院信息工程学院 湖北 武汉 431400) 2(武汉理工大学计算机科学与技术学院 湖北 武汉 430070) 3(交通物联网技术湖北省重点实验室 湖北 武汉 430070)

0 引 言

离群点检测作为数据挖掘技术下的一个重要子项，被广泛应用于欺诈检测和网络入侵检测[1]以及工业系统故障检测[2]等。随着信息检索和数据挖掘技术的迅速发展，离群点检测的相关的研究也在持续发展。近年来，提出了一系列离群点检测方法，其中，孤立森林算法是由Liu等[3]提出的无监督离群点检测集成方法，因其时间复杂度低、精度高而受到工业界和学术界的广泛关注。Staerman等[4]使用孤立森林来检测功能数据中的异常，通过对函数空间的随机划分，解决了函数空间具有不同拓扑结构、异常曲线具有不同模态特征的问题。徐东等[5]提出了SA-iForest算法，利用模拟退火算法去除相似度高的孤立树，选择精度高和差异性大的孤立树组成孤立森林然后用于检测，在准确率、效率和泛化能力方面都有所提高。

局部离群因子是基于密度的经典离群点检测算法，因其简单性和有效性被广泛应用于现实场景下的离群点检测，如多工况过程故障检测[6]。现有的研究在局部离群因子算法的基础上主要针对以下三个方面进行了改进：① 为了提升算法的检测效率，刘芳等[7]提出了快速的 Top-n 局部离群点检测算法(MTLOF)，设计了融合索引结构和多层LOF上界的多粒度剪枝方法来提高检测效率。② 为了提高LOF的精度，Tu等[8]提出了谱角和局部离群点(SALOF)算法，通过计算每个簇类中各数据点的k近邻，得到所有数据点的可达距离和局部可达密度，并依据事先设置好的分割阈值得到数据点的异常概率。③ 针对LOF的超参数选择问题，Xu等[9]提出了一种优化方法，即联合调整LOF超参数k进行离群点检测的启发式策略。

由于缺乏离群点的相关先验知识，依赖于数据全局分布及先验知识的传统离群点检测方法无法有效地检测出离群点。局部离群因子通过计算给定数据点的局部偏差来发现离群点，拥有检测局部离群点的优势并且不依赖于数据集的先验知识及全局分布。通常，离群点在数据集中所占比例相对较小，而现有研究中基于局部离群因子衍生出的多数方法在检测时需要计算所有数据点的lof值，算法效率受到了较大影响，使其无法适用于大规模多维数据集的离群点检测。孤立森林拥有线性时间复杂度且对于全局离群点的识别有着较高的精度，但在应用于大规模多维数据集的检测时，采用全局异常标准无法准确检测出局部离群点，常常出现精度差和效率低等问题。因此，本文提出了FSIF-HDLOF方法，即利用优化iForest剪枝方法最大限度地剪枝掉原始数据集的高密度空间数据点，输出规模较小的离群点候选集用于优化LOF的精确检测，从而提升检测的精度和效率。

1 相关工作

孤立森林算法是一种具有线性时间复杂度的无监督离群点检测方法。通过对原始数据集多次随机采样，再对每次采样后的数据对象随机选择特征进行划分构建等价于二叉搜索树的孤立树，最后形成孤立森林。

局部离群因子算法是一种基于数据密度的离群点检测算法，聚焦在数据点的邻域密度，将具有低密度的数据点视为离群点。LOF算法的一些主要概念如下：

定义1dist(di,dj)：表示数据点di到数据点dj的欧氏距离。

定义2k距离(k_dist(di))：将数据点di到其他数据点的距离从小到大排序，数据点di到第k个数据点的距离即为k距离。

定义3k距离邻域(Nk(di))：到数据点di距离小于k_dist(di)的数据点集合。

定义4可达距离(reach_distk(dr,di))：数据点dr到数据点di的可达距离为数据点dr的k距离和数据点di到数据c点dr间距中的最大值。

定义5局部可达密度(lrd(di))：数据点di的k距离邻域Nk(di)内的所有数据点到数据点di的平均可达距离的倒数。

定义6局部离群因子(lof(di))：数据点di的k距离邻域Nk(di)中所有点的局部可达密度与数据点di的局部可达密度之比的平均数，定义为：

(1)

2 整体框架

图1显示了融合孤立森林与局部离群因子的离群点检测方法的总体流程，主要包括以下两个阶段：

(1) 剪枝阶段：将原始数据集输入基于数据降维和阈值优化的剪枝方法算法，利用NMIFS选出特征子集，然后对特征子集对应的所有数据点进行采样构建孤立森林，再定义特征离群系数计算剪枝阈值得到离群点候选集。

(2) 检测阶段：利用基于信息熵加权的归一化欧氏距离计算得到离群点候选集的距离矩阵，再利用DPCA聚类，根据所得簇类信息计算簇类近邻数来设置LOF的超参数k近邻，计算每个数据点的lof值。最后，结合数据点在剪枝阶段所得的异常分数Score以及在精确检测阶段所得的lof值，通过加权融合的离群分数来确定最终离群点集。

图1 融合孤立森林与局部离群因子的离群点检测方法框架

3 FSIF剪枝方法

3.1 NMIFS数据降维优化策略

由于大规模多维数据集的高度稀疏及噪声较多等特殊性质，在使用孤立森林进行剪枝时，存在着两点不足：① 大量的特征信息未被使用，算法可靠性降低；② 可能存在的大量噪声或无关特征会影响孤立树的构建，算法精确度不高。因此本文考虑在剪枝前采用数据降维方法对原始数据进行降维处理，以降低多维特征对构建孤立树的影响并提升算法的效率。一般情况下，特征选择需要结合数据标签的使用，而进行离群点检测的大规模多维数据集常无对应的标签，因此需要从数据本身出发，理解数据特性及特征之间的关联性，针对性地选择适用的特征选择方法。综上，本文采用更适合现实应用场景的基于标准化互信息(Normalized Mutual Information，NMI)的无监督式特征选择算法[10]。

3.2 特征离群系数用于阈值优化

通常，在一个特定的数据集中不同特征具有不同的实际含义，特征的数值范围也会有差异，而离群点的存在则会影响每个特征的离散程度。因此，本文通过数据特征统计分析得到特征的离散程度，定义特征离群系数来度量数据集的离散度，并通过计算得到剪枝阈值。

定义特征fj的特征离群系数Disp_coe(fj)为：

(2)

通过特征离群系数向量即可计算得到剪枝阈值θD。式(4)中，DNorm-Top(s)是指采用Top()算法快速获取Df中特征离群系数较大的s个值，s为NMIFS对D降维后Fs中特征的数量，调节因子α为区间[0.45, 0.55]之间的随机数。通过孤立森林算法计算每个数据点的异常分数并降序排序，将前n×θD条具有较大异常分数的数据点归入离群候选集。

(3)

(4)

4 HDLOF检测方法

原始LOF存在一些明显的不足，如通过欧氏距离计算点距没有考虑数据集不同特征的重要程度，超参数k近邻的随机或者凭经验选取，都会影响数据点的lof值计算，从而影响LOF对离群点检测的准确性。因此，本节针对以上不足进行了改进，提出了基于邻域优化的局部离群因子算法(HDLOF)。改进后的算法使用更加精细的基于信息熵加权的归一化欧氏距离来计算数据点之间的距离，超参数k近邻的值采用基于DPCA聚类后簇类信息而计算所得的簇类近邻数来设置，离群点由最终加权融合的离群分数确定。

4.1 基于邻域优化的局部离群因子精确检测

4.1.1基于信息熵加权的归一化欧氏距离

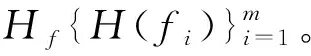
(5)

(6)

数据点di与数据点dj间的信息熵加权欧氏距离为H_dist(di,dj,wf)，计算式如式(7)所示。为消除特征之间的量纲影响，在信息熵加权的欧氏距离基础上，对距离进行归一化，最后数据点di与数据点dj间基于信息熵加权的归一化欧氏距离如式(8)所示。

(7)

(8)

4.1.2基于密度峰值的超参数优化策略

一般而言，数据集可以划分为几个簇类，而同一簇类的数据点相似度较高，每个簇类内数据点可设置相同的参数k，不同簇类的数据点可根据其所在簇类信息设置相应的参数k。Rodriguez等[11]2014年提出的快速密度峰值聚类算法(DPCA)能很好地识别任何形状的簇类，具有很强的泛化能力。因此，本文利用该聚类算法对上一阶段孤立森林剪枝方法输出的离群点候选集进行快速聚类，并根据簇类结果，为不同簇类的数据点设置不同的超参数k。

DPCA聚类结束得到c个簇类中心以及数据点所属簇类，统计可得各簇类数据点个数{s1,s2,…,sc}。本文提出了簇类近邻数(cluster_k)的概念，将其设置为某个簇类中所有数据点的超参数k近邻值，第i个簇类中数据点的簇类近邻数表示为cluster_ki，对应计算式为式(9)，其中，si为第i个簇类中数据点的个数。

(9)

4.2 HDLOF精确检测实现

本节结合剪枝阶段所得数据点d的异常分数Score(d)以及本节精确检测所得的lof(d)，根据式(10)计算得到数据点d最终的离群分数lof-Score(d)。其中，β为融合权重。在FSIF-HDLOF中，HDLOF用于精确检测，具有更高可信度，因此赋予lof值较大权重，β建议取值范围区间[0.7, 0.9]。

lof-Score(d)=(1-β)×Score(d)+β×lof(d)

(10)

HDLOF具体实现步骤如算法1所示。

算法1HDLOF检测实现

输入: 离群点候选集OC，数据点的平均异常分数Score(c)，异常数量m。

输出: 离群点集OutlierSet(O)。

①HNorm_dist(ci,cj,wf)；

/*根据式(8)计算离群点候选集

的距离矩阵*/

② cluster_ki；

/*根据式(9)计算数据点的簇类近邻数，即超

参数k值*/

③lof(c)； /*根据式(1)计算所有数据点的局部离群因子*/

④lof-Score(c)；

/*根据式(10)计算所有数据点最终离群分

数*/

⑤O； /*取lof-Score最大的Top(h)个数据点作为离群点*/

⑥ returnO

/*返回离群点集*/

5 实验与结果分析

5.1 实验数据与实验环境

为了全面地评估算法性能，本文所有实验均在以下介绍的五个不同规模数据集上进行。数据集Satellite、Mnist、Shuttle以及Smtp均来自于Outlier Detection DataSets (ODDS) 网站，其出现在很多文献[3,12-13]上被用于评估离群点检测算法的性能。五个数据集具体信息如表1所示。

表1 数据集的详细信息

实验环境：本文基于Python来处理数据集、实现剪枝和检测算法及性能验证，实验均在同一笔记本电脑上运行。设备硬件配置为：Intel i5-3337U CPU @ 1.80 GHz 双核四线程处理器，8 GB内存，Python版本为3.6.4。

5.2 评价指标

5.2.1剪枝精度评价指标

基于数据降维和阈值优化的孤立森林作为FSIF-HDLOF的剪枝方法，其目的是在保证离群点不被剪枝掉的情况下，剪枝掉尽可能多的正常数据以减少后续LOF的计算量，从而提升整体的算法效率。考虑到剪枝比例会在不同程度上影响LOF检测的准确度，因此本文将同时使用剪枝占比和剪枝准确率来衡量剪枝算法的高效性和准确性。

剪枝准确率(Pruning Precision，PP)，即离群点候选集中真实离群点的数量与离群点候选集数据点总数的比值，公式为ρPP=ρTP/(ρTP+ρFP)。一般PP值越高，表示在离群点候选集中，真正的离群点所占比例越大，剪枝后留下的正常数据越少，剪枝效果越好。剪枝占比(Pruning Number，PN)是指被修剪数据点的百分比，即被剪枝掉的数据点数量与数据集数据点总数的比值。通常，在PP较高的情况下，PN越大，说明算法剪枝效果越好。

5.2.2检测精度评价指标

大部分离群点检测算法为无监督形式，为了准确评估及对比不同算法的检测效果，本文实验所用数据集均为带标签数据集。因此，本文利用传统的常用评价指标Precision和F1-Measure来评估离群点检测算法的性能，其中F1-Measure是Precision和Recall加权调和平均，作为综合评价指标更具有代表性。

5.3 实验方法性能评估

为了验证本文所提的FSIF-HDLOF对大规模多维数据集离群点检测的有效性，将FSIF-HDLOF与离群点检测领域上常用算法，如原始Isolation Forest(IF)、原始LOF、KMeans-LOF(K-LOF)[14]和R1SVM[15]这五个方法在五个不同规模的数据集上进行对比实验。其中，FSIF和K-Means分别用于FSIF-HDLOF和K-LOF算法剪枝阶段。

5.3.1剪枝方法性能评估

剪枝方法FSIF和K-Means在数据集上的实验结果如表2中所示，FSIF的剪枝准确性及剪枝占比均高于K-Means算法。分析发现，K-Means用于剪枝的思想是：聚类之后，根据某种规则将数据点数量少的簇类整体或者簇类中的部分数据点归入离群点候选集。因此，这种剪枝方式极大容易受到聚类过程的影响，而K-Means的聚类结果往往具有很大的随机性，造成了其用于剪枝的恶劣结果。孤立森林则相比使用了聚类思想的剪枝方法而言要优胜许多。

表2 实验方法在数据集上的剪枝性能

5.3.2融合方法性能评估

1) 检测精度指标。图2为上述五个算法在数据集上检测结果的混淆矩阵，左纵坐标为数据集名称，下横坐标为五个算法，右纵坐标为检测的标签，上横坐标为真实标签，其中0代表离群点，1代表正常数据。每四个格子为一个算法对一个数据集的检测结果。从图2中可看出，五种算法均能检测出绝大部分正常点(即TN)，但都存在着部分误检。其中，FSIF-HDLOF表现相对优异，其所检测的TN和TP总数均高于其他算法。

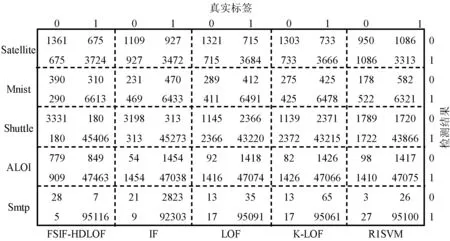
图2 实验方法在数据集上的混淆矩阵

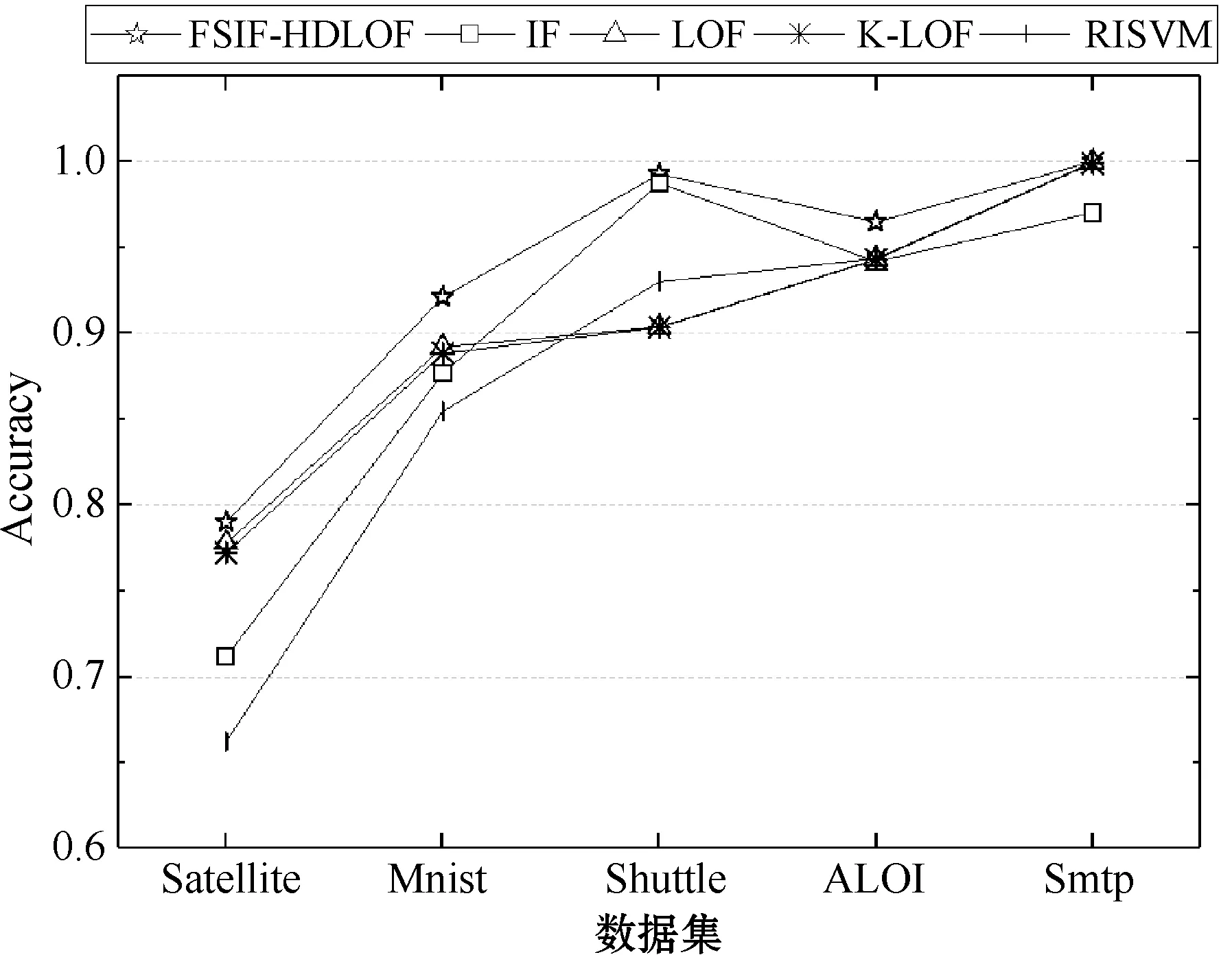
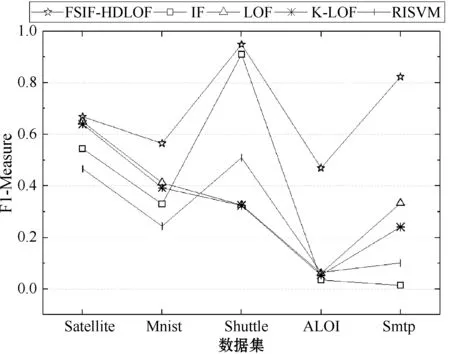
图3 实验方法在数据集上的Accuracy、F1-Measure

图3展示了五个对比算法在数据集上的Accuracy和F1-Measure结果，可以看到所提出的FSIF-HDLOF在不同数据集上都表现出了相比其他算法更好的性能和更加稳定的检测效果。特别地，对于大规模多维数据集ALOI和大规模数据集Smtp，其正常数据点与离群点的比例极其不平衡。分析可知，单一的离群点检测方法对所有数据采用同一种异常标准，无法综合考虑数据的全局和局部信息。当大规模多维数据集的正常点与离群点的比例极其不平衡时，采用统一标准的单一离群点检测方法无法准确检测出离群点。融合方法FSIF-HDLOF通过初步剪枝，使得离群点候选集的分布不再极端化，并结合数据的全局异常信息以及局部离群程度来综合确定离群点，大大提高了极不平衡数据的检测精度。

2) 运行时间成本。运行时间成本是指在标准软硬件系统上进行离群点检测所花费的时间，包括数据预处理时间和检测计算时间。FSIF-HDLOF和K-LOF算法的预处理时间为FSIF和K-Means的剪枝耗时，R1SVM算法的预处理时间为数据集随机化的耗时，而IF和LOF只有离群点检测计算时间，在数据集上运行时间如图4所示。 除Mnist数据集外，IF在剩余4个数据集上的运行速度最快，由此验证了利用其对原始数据集进行剪枝的合理性。FSIF-HDLOF由于使用了LOF进行精确检测，因此其效率不如IF，但因为结合IF的使用，其在大规模数据集Shuttle和ALOI上的检测速度远高于LOF。

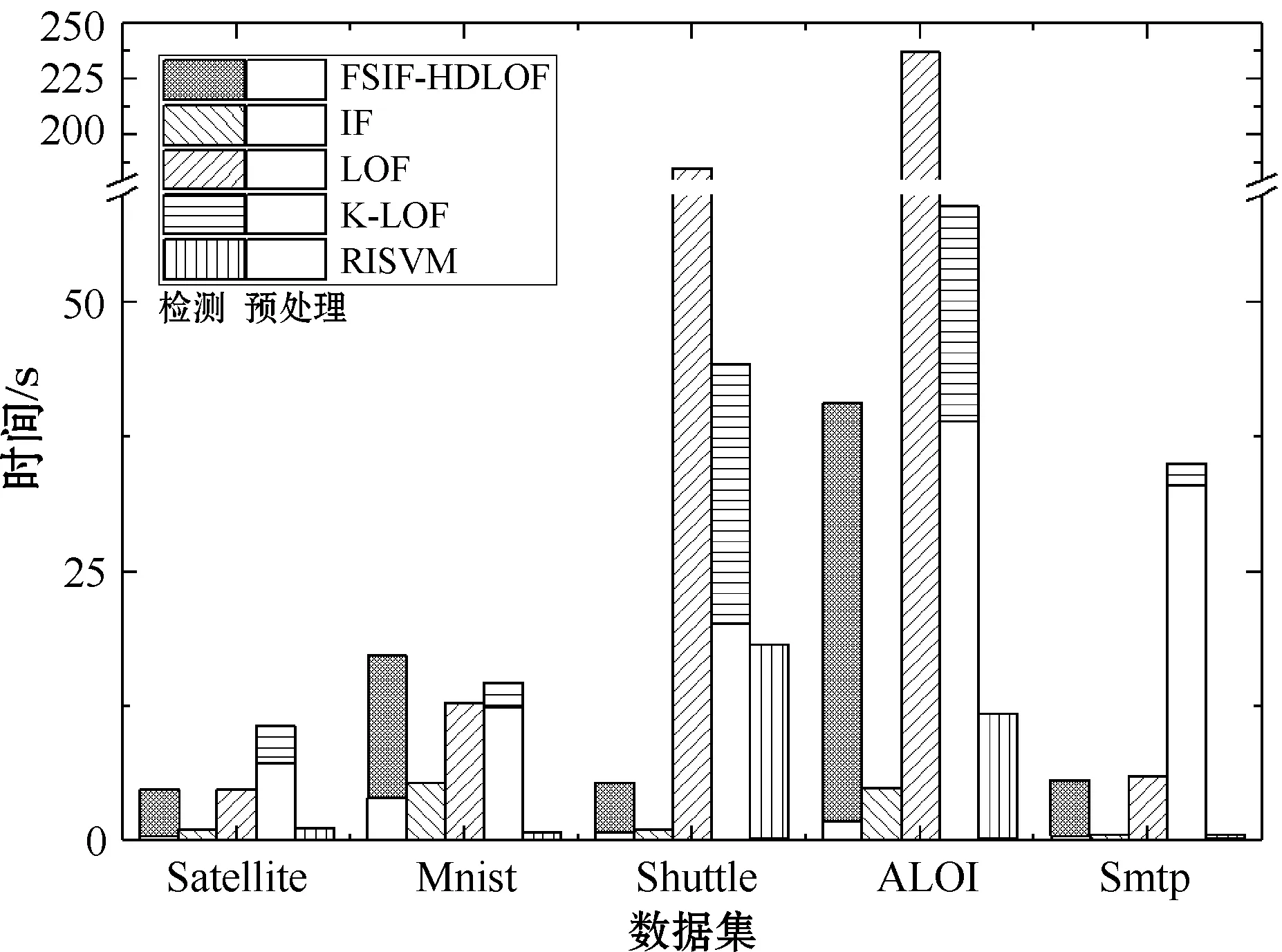
图4 实验方法在数据集上的运行时间

6 结 语

在大规模多维数据集中，为了更有效地检测离群点，本文提出一种新的融合方法。该方法融合iForest和LOF来检测离群点，并针对剪枝阶段iForest和检测阶段LOF的不足进行了相应改进。采用基于数据降维和阈值优化的iForest对原始数据集进行剪枝，得到较小规模、高质量的离群点候选集待进一步精确检测。基于离群点候选集，提出的阈值优化局部离群因子方法能有效地检测离群点。五个数据集用来评估本文算法的性能，与其他算法相比，本文算法检测精度明显优于其他算法，实现了检测精度与效率的良好平衡，在大数据量且低离群点比例的数据集ALOI和Stmp上优势更明显。