相关性和显著性结合的制导工具误差系数分离方法

魏宗康，高荣荣，赵 友

（北京航天控制仪器研究所，北京 100854）

惯性制导工具误差分离精度对于提升弹道导弹命中精度有着举足轻重的意义。在利用弹道导弹遥外测数据分离惯性测量系统误差系数时，可采用遥外测速度误差作为观测量，其优点是速度误差反映了加速度计组合和陀螺仪组合的测量误差，另外一个优点是建立速度环境函数矩阵后可直接通过解方程求解误差系数，过程中没有微分计算。

基于速度环境函数的遥外测误差分离时，首先要确定误差模型的结构。弹道导弹飞行轨迹的特点是惯性系统只工作于主动段，而不能全姿态任意方位都存在大过载或大机动，这就决定了选择的误差模型结构矩阵中部分系数之间具有相关性，而最小二乘法对于强相关结构矩阵有较低的适应能力，会导致分离的误差系数偏离真值较大。为此，如何在强相关条件的约束下，实现基于弹道导弹遥外测数据的惯性测量系统误差系数的精确分离是一个难题。为解决该问题，文献[1]采用灵敏度理论对制导工具误差进行分离，通过比较两个误差系数的灵敏度曲线变化趋势的一致性来判断两个误差系数的相关性，但是此方法的缺点是没有具体的量化指标。文献[2]和文献[3]分别提出了主成分估计、偏最小二乘估计、岭估计法、粒子群算法等不同的估计方法，这些方法的核心思想是在模型不降阶的前提下估计出系数的近似解，但这些方法带来的问题就是估计有偏差，没有从根本上解决惯性制导工具误差系数的精确分离问题。文献[4]采用显著性分析方法对石英加速度计的二次项误差系数进行分离，但是并没有考虑误差系数之间的相关性问题，分离方法缺乏严谨性。

针对该问题本文提出了一种把相关性检验和显著性检验分阶段结合起来的惯性制导工具误差分离方法，重点不是在于估计结构矩阵相关时的每个系数，而是估计不同相关系数之间组合后的值，采用该方法后分离的结果更准确，也较符合工程实际。

1 惯性测量系统高阶误差模型

加速度计组合的高阶误差模型分别为[5-6]：

式(1)中，k0x、k0y、k0z为x、y、z加速度计的零偏，单位为g；δkx、δky、δkz为x、y、z加速度计的线性度误差；δKax、δKay、δKaz为x、y、z加速度计的线性度不对称性误差；k yx、k zx、k xy、k zy、k xz、kyz为x、y、z加速度计的安装误差角，单位为rad；K2x、K2y、K2z为x、y、z加速度计的二次项误差系数，单位为g/g2；δK2x、δK2y、δK2z为x、y、z加速度计的奇二次项误差系数，单位为g/g2；K xxy、K xxz、K xyz、Kyxy、Kyxz、Kyyz、Kzxy、Kzxz、Kzyz为x、y、z加速度计的交叉耦合项误差系数，单位为g/g2；K3x、K3y、K3z分别为x、y、z加速度计的三次项误差系数，单位为g/g3。

陀螺仪组合的高阶误差模型为[7-8]

式(2)中，DFx、DFy、DFz为x、y、z陀螺仪的常值漂移，单位为°/h；D1x、D1yD1z、D2x、D2y、D2z、D3x、D3y、D3z为x、y、z陀螺仪的一次项漂移，单位为°/h/g；D4x、D4y、D4z、D5x、D5y、D5z、D6x、D6y、D6z为x、y、z陀螺仪的二次项漂移，单位为°/h/g2；D7x、D7y、D7z、D8x、D8y、D8z、D9x、D9y、D9z为x、y、z陀螺仪的交叉耦合二次项漂移，单位为°/h/g2。

2 遥外测速度误差

对于在弹道导弹主动段关机点就结束工作的惯性系统来说，由于时间较短，可在误差分析时忽略各反馈回路的影响，简化的导航误差传播流程见图1。

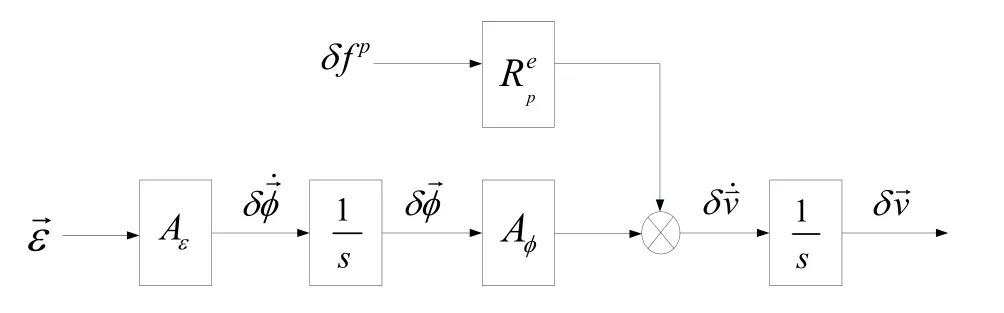
图1 基于地球坐标系的导航误差传播开环流程图Fig.1 Open-loop flow chart of navigation error transmission based on earth coordinate system

采用上述简化误差模型的优点是可直接对姿态微分方程、速度微分方程和位置微分方程进行积分，对应列写出各项惯性仪表误差系数的环境函数矩阵，采用最小二乘法直接求解误差系数，该求解方法相对简单[9]。图1 中，

Aε——由陀螺漂移引起姿态角速度误差时的变换矩阵；

Aφ——由姿态角误差引起速度误差变化量时的变化矩阵；

根据速度误差传播方程即可列写出把陀螺仪、加速度计各项误差系数对应的速度环境函数[10]。速度误差方程的模型结构为：

上式采用矩阵形式可写为：

其中，Y表示速度误差矩阵；C表示速度环境函数矩阵；X表示惯性器件的误差系数。

3 主成分估计的缺陷

当结构矩阵C不为维列满秩时，则不能用最小二乘法求解[11-12]。所谓主成分估计就是把信息矩阵Φ=CTC中较小的特征值近似简化为0，然后求解X的过程。

当C不为列满秩时，Φ的特征值λ1、λ2…λm中至少有一个为0。为分析方便，设λ1、λ2、…、λm为从小到大排序后的结果，则D=diag（λ1,λ2…λm）可写为：

其中，ΛB为对角线所有元素非零的对角阵。

根据矩阵D对应的正交变换矩阵表示为：

则有：

由于PA为信息矩阵Φ=CTC的特征值0 对应的特征向量，有

对上式可解出：

由此可知，当C不为列满秩时，求解方程Y=CX等价于求解方程：

一种求解X的应用较广但不准确的方法是，令：

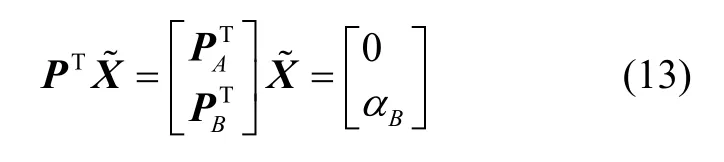
可得到：

因此，采用主成分估计时，仍然需要非相关处理。只有在对结构矩阵进行降维处理后，才可求得部分系数的解。主成分辨识法的另外一个缺点是特征值大并不意味着对应误差系数也显著，因此，主成分估计方法无法识别误差系数在实际使用中的最优估计问题[13]。

4 结合相关性和显著性的辨识方法

针对结构矩阵不为列满秩的情形，本节的研究思路则是对模型适当降阶以求出各系数不同组合的精确解[14]。

4.1 结构矩阵列向量相关时的系数计算

在结构矩阵不为列满秩时，则必然有相应的列向量相关。在求解系数时，可先找到结构矩阵中最相关的列后，去掉其中的一列来对该结构矩阵进行简化[15]。

下面给出相关性定义，设有向量Ci（i=1,2…m）为结构矩阵的列矩阵，当Ci全不为零时，若有某些非零标量αi（i=1,2…m）满足：

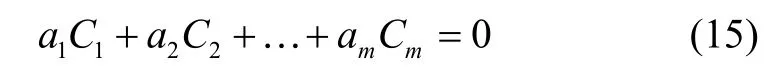
则称向量C1、C2···Cm线性相关。

若仅当：

时式(15)才成立，则称向量C1、C2···Cm线性独立，或不相关。

为分析方便，设向量C1、C2···Cj-1、Cj、Cj+1、···Cm线性相关，且αj非零，则必然存在某些非零标量rj,i（i=1,2…j-1，j+1…m）满足：

把Cj代入线性方程Y=CX中，有：

4.2 辨识具体步骤

显著性检验只是解决了因子与输出的关系，但不能解决因子之间的相关性问题；相关性检验只是解决了因子之间的相关性问题，而没有解决因子与输出的显著性问题。下面试图把显著性检验和相关性检验结合起来以辨识系统的系数。

在结构矩阵中存在相关的两个列时，采用离线最小二乘法时信息矩阵CTC的行列式将近似为0，此时分离的系数值将严重偏离真实值，甚至无法求解。虽然采用显著性检验可以简化模型的结构，但这种简化也存在一个缺点，就是在结构矩阵奇异或近似奇异时有可能把两个相关的变量都作为显著项而保留到模型结构[16]。

为解决奇异线性系统的离线系数辨识问题，在本节提出一种综合相关性和显著性的辨识方法。就是对一个考虑到各种因子的线性系统模型结构，先对该模型结构进行相关性检验并简化模型结构，直至结构矩阵的所有列之间互不相关；然后，对简化模型进行显著性检验并在此基础上进一步简化模型结构，直至最终的模型结构为列满秩，且对应的系数都显著。

具体步骤为：

(1) 求出结构矩阵的基向量，并以所有的基向量构成基矩阵；

(2) 对结构矩阵中除了基矩阵之外的列向量，求出用基矩阵表示的系数，这些系数用于构建基矩阵对应的新的待估计状态变量；在求解过程中采用显著性检验，把不显著的系数直接置为零；

(3) 根据基矩阵和观测向量，求解出新的状态变量的值；在求解过程中采用显著性检验，把不显著的状态变量直接置为零。

5 采用高阶误差模型的工具误差系数分离

遥外测速度误差如图2，可以看出，速度误差随着时间积累。

图2 遥外测速度误差的拟合结果Fig.2 Fitting result of remote measurement velocity error

先对高阶误差模型进行相关性检验[9-10]，在环境函数矩阵中选取46 个列作为基，这46 个列对应的误差系数分别为ΔT、k0x、δKax、kyx、Kxxy、Kxyz、K3x、k0y、δKay、kxy、kzy、δK2y、Kyxy、Kyyz、K3y、k0z、δkz、δKaz、kyz、Kzxy、Kzyz、DFx、DFy、DFz、D1x、D1y、D1z、D2x、D2y、D2z、D3y、D3z、D4x、D4z、D5x、D5y、D5z、D6x、D6z、D7x、D7y、D7z、D8x、D8y、D8z、D9z。由这46 个基构成基矩阵C′，另外18 个系数δkx、kzx、K2x、δK2x、Kxxz、δky、K2y、Kyxz、kxz、K2z、δK2z、Kzxz、K3z、D3x、D4y、D6y、D9x、D9y对应的列向量都可表示为基的线性组合，这些列向量构成矩阵C″。

C″中的每一列都可用C′中基的线性组合表示，设m=64、d=46，用矩阵方程描述为

式中，p1=3、p2=6、p3=7、p4=8、p5=10、p6=14、p7=18、p8=21、p9=27、p10=29、p11=30、p12=32、p13=34、p14=44、p15=48、p16=54、p17=62、p18=63；q1=1、q2=2、q3=4、q4=5、q5=9、q6=11、q7=12、q8=13、q9=15、q10=16、q11=17、q12=19、q13=20、q14=22、q15=23、q16=24、q17=25、q18=26、q19=28、q20=31、q21=33、q22=35、q23=36、q24=37、q25=38、q26=39、q27=40、q28=41、q29=42、q30=43、q31=45、q32=46、q33=47、q34=49、q35=50、q36=51、q37=52、q38=53、q39=55、q40=56、q41=57、q42=58、q43=59、q44=60、q45=61、q46=64。

矩阵R中各元素的值可通过采用最小二乘法求得，但需强调的是，经过显著性检验后有些元素值可置为零，从而简化方程。比如，

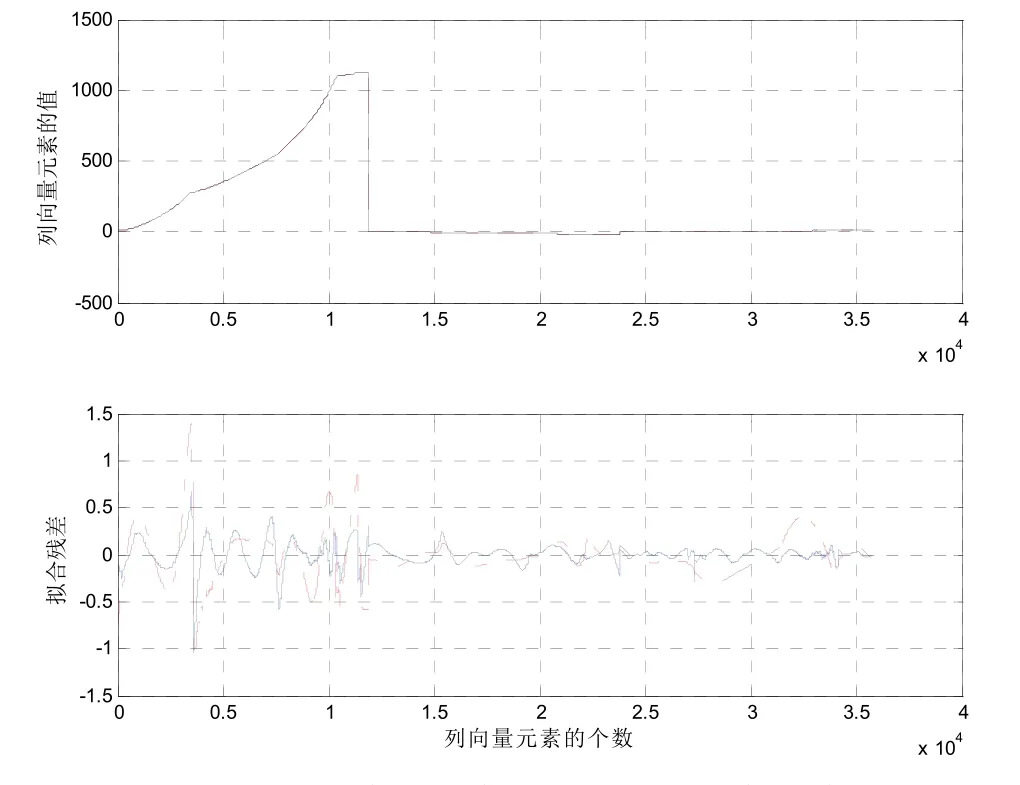
图3 δkx 对应的列向量元素及其拟合残差Fig.3 Contrast of δkxvalue and its’ fitting residual error in different conditions

图4 δky 对应的列向量元素及其拟合残差Fig.4 Contrast of δkyvalue and its’ fitting residual error in different conditions

在求解出矩阵R中的各元素后，考虑到相关性后的基于遥外测速度差的因果关系如图5 所示。

图5 结构矩阵列相关时的遥外测速度差因果关系图Fig.5 The causality diagram of remote measurement velocity error when the structure matrix columns are correlated

重新定义一组新的误差系数：

基于新的误差系数的遥外测速度差因果关系如图6 所示，其结构矩阵为列满秩，用线性函数进行描述见式(28)。

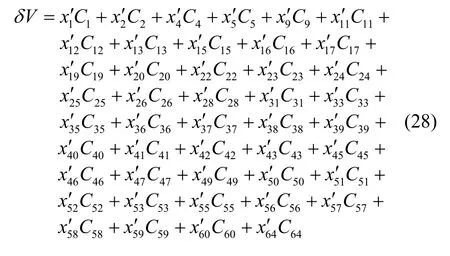
图6 结构矩阵列满秩时的遥外测速度差因果关系图Fig.6 The causality diagram of remote measurement velocity error based on new error coefficient

再采用最小二乘法并经显著性检验后，保留显著项后的遥外测速度差因果关系如图7 所示，表达式为：

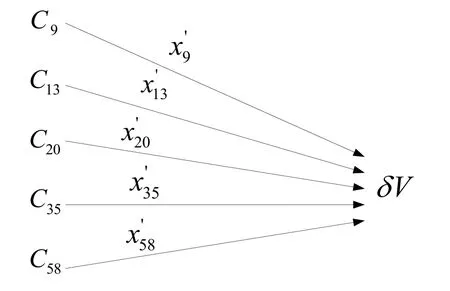
图7 保留显著项后的遥外测速度差因果关系图Fig.7 The causality diagram of remote velocity error retaining significance

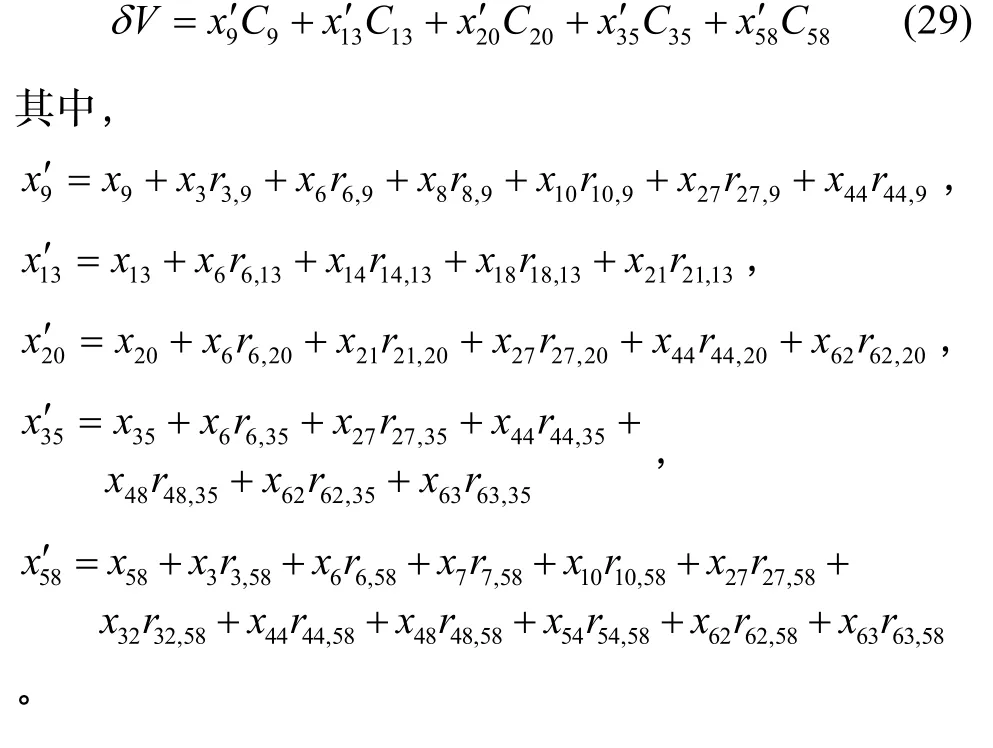
最终得到显著的惯性器件误差模型为：

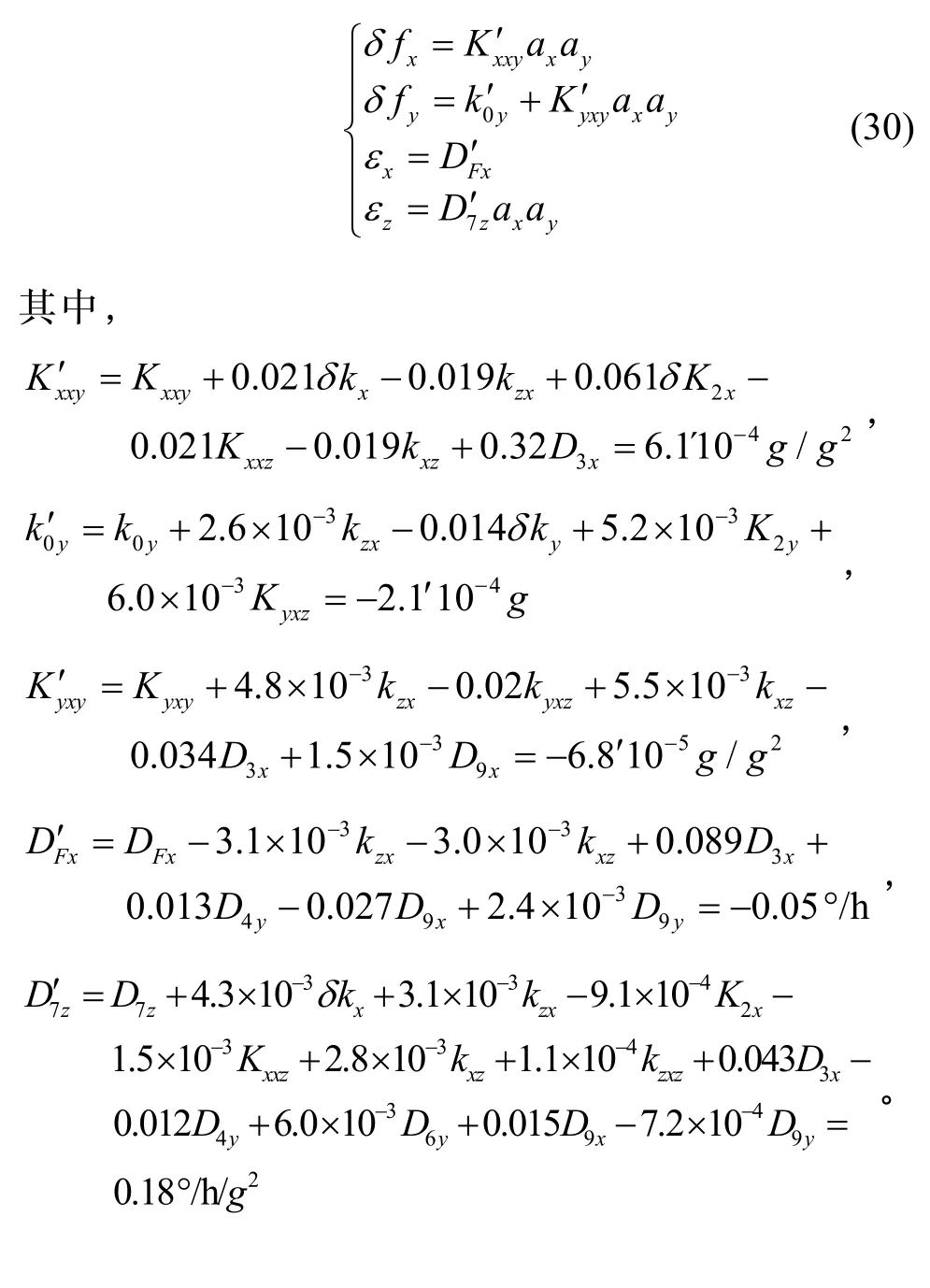
除上述系数显著外，其余各项误差系数都不显著。误差系数不显著的原因分为三种，第一种原因是在地面上零次项和一次项误差系数都已进行了补偿，第二种原因是有些高阶误差项在飞行条件下不能充分激励，第三种原因部分误差只是数学描述而并不存在明确的物理意义。

图8 遥外测速度误差补偿残差曲线Fig.8 Residual curve of remote velocity error compensation

6 结论

本文给出了一种结合相关性检验和显著性检验的提高惯性制导精度的方法，通过引进环境函数矩阵到相关检验中，把相互之间关联的制导工具误差系数进行整合，重构出新的遥外测速度误差模型。整合后的新系数对应的环境函数矩阵为列满秩，从而可精确求解误差系数，克服了主成分估计、岭估计等方法不能精确求解的缺点。把显著性检验引入制导工具误差系数分离过程中，有利于简化模型，也有利于分析各制导工具误差系数与测量值之间的本质特性，并且能够大幅降低模型的维数，克服了结构矩阵维数过多的问题，具有简单快捷、容易实现的优点。将采用本文提出的方法分离得到的误差系数代入遥外测速度误差模型，计算得到的拟合残差大部分在±0.2 m/s 之内，计算结果表明本文所提出的方法可以有效、准确地分离惯性制导工具误差系数，在惯性制导精度提升领域具有很好的应用价值。