指定性能指标的运载火箭姿控系统设计

张 亮，李丹钰，崔乃刚

（1.中山大学航空航天学院，深圳 518107；2.哈尔滨工业大学航天学院，哈尔滨 150001）

2021 年中国航天共实施了55 次发射任务，发射次数位居世界首位，其中包括火星探测、空间站、探月工程等国家重大工程任务。2 月，天问一号顺利进入环火轨道，成为中国第一颗人造火星卫星。4 月，长征五号B 运载火箭携带天和号核心舱于海南文昌发射场起飞，标志着中国空间站建造任务的全面开启。6月，长征二号F 遥十二火箭携带神州十二号成功发射，载着中国三位宇航员成功与天和核心舱完成对接。在国外，SpaceX 公司的猎鹰火箭重复使用，使得航天发射成本极大降低，有效促进了航天科技的发展。然而，在未来高密度火箭发射需求下，如何快速设计出性能更好的姿态控制系统尤为关键。

在运载火箭姿态控制系统设计中，传统的方法是采用三通道解耦的PID 控制，基于频域设计方法和校正网络来获得足够的幅值裕度和相位裕度等性能。然而，PID 控制存在一些不足，比如设计流程复杂、参数众多、设计周期长等，难以满足我国高密度发射需求。因此一些学者在PID 的基础上开展改进设计，如徐世昊[1]等针对典型串联构型的火箭模型，在传统PD+校正网络控制的基础上，设计了自适应增广控制模块，提高了复杂飞行条件下的控制性能，但也存在参数调节规律不明确的缺点。然而，无论如何改进PID控制，其姿态跟踪误差还是比较大，难以适应强耦合的捆绑火箭姿态控制[2]。为此，张亮等[3]改进了传统自抗扰控制器，利用两次非线性控制律得到加速度指令，并且采用非线性扩张状态观测器补偿了火箭状态空间模型中的不确定性。相较于PID 控制器，该控制器具有设计过程简单和控制精度更高的优点，但计算量较大，公式复杂。对于强非线性、参数时变的运载火箭模型，采用时不变模型设计的控制器会导致跟踪精度较低，为此刘飞等[4]设计了微分包含镇定控制器，解决了大范围参数不确定的问题，但该控制器有一定的保守性，适用范围受限。通过干扰观测器可以对建模不确定性和干扰进行补偿[5]，Ma 等[6]研究了基于反步法和有限时间状态观测器的控制技术。然而有限时间收敛控制器有高度依赖于初始条件的缺点，为此田野等[7]设计了一种新型的固定时间非奇异终端滑模控制方法，可有效解决该问题。但是，固定时间收敛控制器的实际收敛时间与多个控制参数有关，无法直观获得，且收敛时间是一个上界存在较大的不确定性。而指定时间收敛可以预先以参数的形式，确定系统的收敛时间，与系统的初值无关。王冠等[8]设计了一种指定时间收敛的自适应控制方法，保证系统状态变量在指定时间上趋于稳定值,但控制器的保守性较强。为了改善现有控制器性能依赖初值且无法实现指定时间收敛的问题，本文将通过反步法推导指定时间收敛的姿态跟踪控制律，它保证了姿态跟踪误差在指定时间上收敛的性能。该控制器的主要优点包括：1）通过设计参考模型可预先设定控制性能指标。2）控制器可以实现高精度姿态跟踪，且收敛时间是与初始状态无关的先验参数。

本文的文章结构如下：首先，在文献[3]的基础上，建立了运载火箭姿态动力学模型。然后，基于文献[9]-[11]作者研究成果和一些数学基础，设计指定时间收敛函数，通过反步法设计出指定时间收敛控制律，然后借助李雅普诺夫稳定性理论，证明了控制器的指定时间收敛性能。最后，通过仿真分析，验证了本文所提出的控制器性能。

1 运载火箭姿态动力学建模

1.1 状态方程的建立

考虑如图1 所示的捆绑运载火箭，在主动段飞行过程中，8 台规格一致的主发动机（单台发动机推力460 t）参与推力矢量控制。其中，每个发动机有两个喷管，助推发动机两个喷管均参与控制，摆角分别为δi（i=I,II,III,IV）,而芯级发动机只有远离火箭轴线的外部喷管参与控制，摆角分别定义为δi（i=1,2,3,4）。

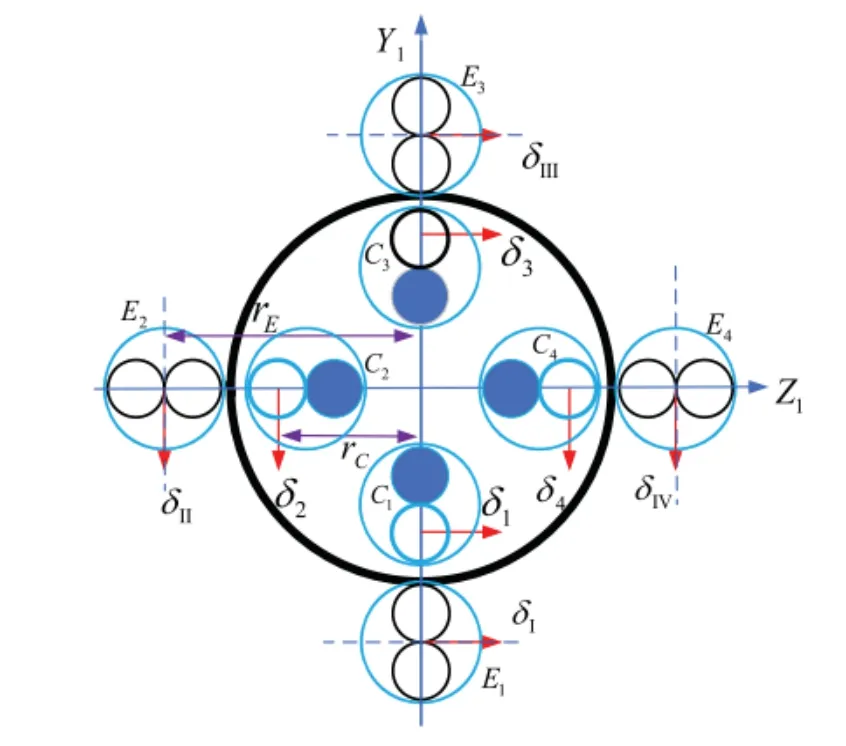
图1 运载火箭的摆动角度分布Fig.1 Swing angle distribution for launch vehicle

此外，r E和rC分别是助推发动机和芯级发动机距离箭体轴线的距离。假设发动机单机推力为P，则每个喷管的推力为P/2。则根据参考文献[3]，可建立如下所示的姿态动力学模型：

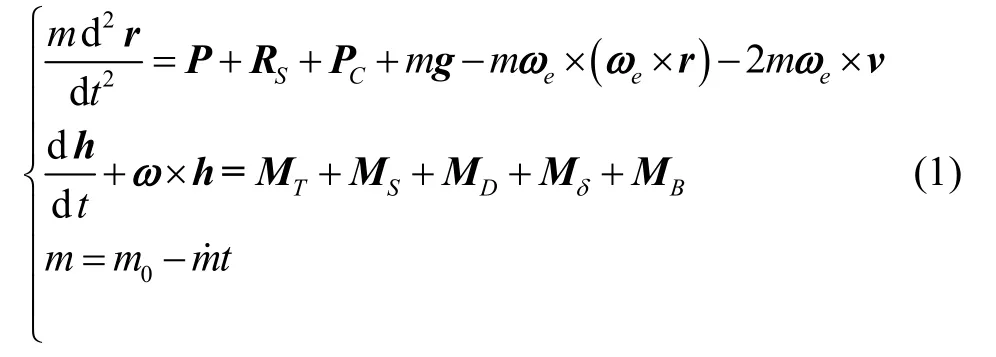
其中，m为火箭的质量，m0为火箭的初始质量值，m˙为8 台主发动机的总秒耗量，t为主发动机工作时间。r、P和RS分别为位置矢量、推力矢量和气动力矢量。PC、g、ωe和v分别代表发动机摆动惯性力、重力加速度、地球角速度和速度。MT、MS、MD、Mδ和MB分别是推力力矩、空气动力力矩、空气动力阻尼、发动机摆动惯性矩和结构扰动或外部扰动。此外，火箭的角速度定义为ω=[ωxωyωz]T，火箭的转动惯量矩阵定义为J=diag（[J xJyJz]），角动量为h=Jω。

另外，可定义状态变量为X1=[γψϑ]T，X2=[ωxωyωz]T和U=[δγδψδϑ]T。其中ϑ为俯仰角，γ为滚转角，ψ为偏航角。δγ、δψ和δϑ代表了控制系统设计的等效三通道独立发动机摆动角。U表示等效发动机摆角向量。则状态空间方程可建立为：其中，θ为弹道倾角，A为实际的风向角，Aw为风矢量角，Af为发射方位角，As为风场数据表中的方向角，Wp为平稳风的风速，Wq为切变风速。

1.2 参考模型设计

为了保证运载火箭在主动段具有良好的动态控制性能，可设计一个有预期超调量和响应时间的二阶系统。假设姿态控制系统的目标就是跟踪预先设计的程序角，则参考模型有如下所示：

2 姿态控制器设计

2.1 引理和定理

为了设计姿态控制器，本文首先引入一些定义和基本引理，考虑如下所示的系统：

简化式(13)就可以得到：

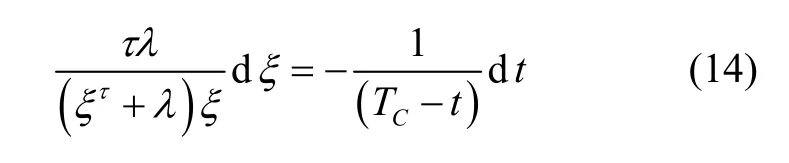
等式(14)两边同时积分可得：

则等式(15)的解为：

2.2 控制律设计

针对前述建立的跟踪误差姿态动力学模型，为了实现对外界干扰的良好跟踪与估计，可设计如下形式的扰动观测器[11]：

其中，Z1、Z2是对式(18)中X1和D的估计值。k1、k2、L1和L2是观测器的增益，0＜p＜1,q＞ 1为幂次系数。

定理 2：针对姿态误差动力学模型式(18)，基于定理1 和扰动观测器式(24)，设计控制器式(21)，则可认为本文设计的控制器是指定时间收敛的。下面给出详细证明过程。

证.定义李雅普诺夫函数为：

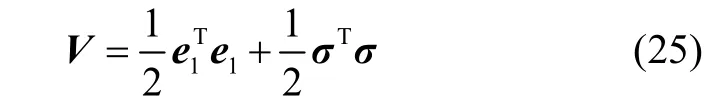
对李雅普诺夫函数求导有：

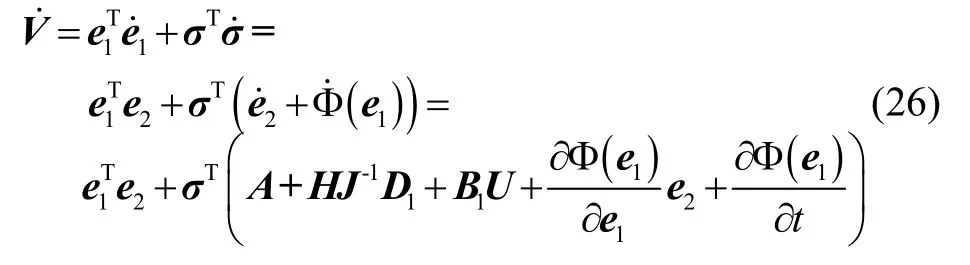
第一步：当t≤TC时，将控制器式(21)代入式(26)，可得：

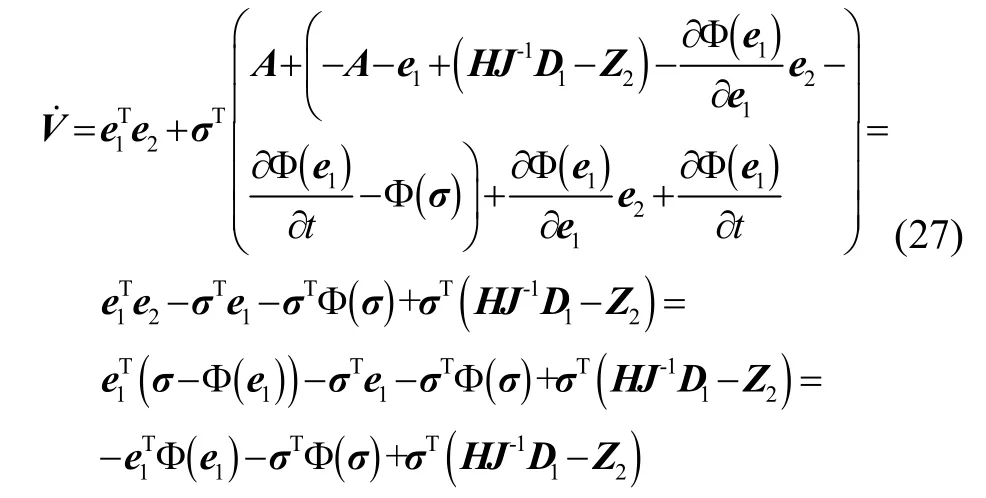
由于扰动观测器式(24)可以实现对扰动的精确估计，因此HJ-1D1-Z2=0，则有：

由定理1 可知，系统是指定时间收敛的，且收敛时间为TC。

第二步：当t＞TC时，有

综上所述，即完成了定理2 的证明。

3 仿真校验

为了验证本文所设计控制器的指定性能指标效果以及性能，引入传统滑模控制器和传统的PID 控制器以作对比分析。

（1）传统滑模控制器[15]

其中，β和b是设计的正实数，需满足1＜b＜ 2。控制律U可设计为：

（2）PID 控制器

其中，KP、KI、KD分别代表比例系数、积分系数和微分系数。

3.1 特征点仿真

为了验证本文所设计控制器的有效性，首先选择了某一个特征点进行分析，如第70 s 火箭飞行状态，具体的火箭参数选取如表1 所示，而控制器参数取为p=2.2，τ=0.4，λ=1.8，TC=2s。观测器的参数设计为k1=k2=20，L1=L2=100，p=0.9和q=1.8。同时，系统的初始条件一般可设置为X1=[0.01 0.01 0.01]Trad，X2=[0.01 0.01 0.01]Trad/s，=[0 0 0]T,UC=[5° 8° 10° ]T。滑模控制器的参数设计为b=1.32,β=0.32,ρ=0.036，而PID 控制器参数为KP=diag（[2.8 20 20]），KI=diag（[0.2 0.3 0.3]）和KD=diag（[0.8 15 15]）。特征点处的大气密度为ρ1=0.3558g/cm3。通过跟踪参考模型，得到的性能指标（以γ通道为例）如表2 所示。随后，针对上述的三种控制器，本文同时开展仿真分析，则仿真结果可参见表3 和图2-4。

表1 火箭特征点处的参数Tab.1 Parameters of the launch vehicle

图2 姿态跟踪响应Fig.2 Attitude tracking response

图3 姿态跟踪误差Fig.3 Attitude tracking errors

图4 等效舵摆角Fig.4 Equivalent swing angles

由表2 可以看出，通过跟踪二阶参考模型的信号，本文提出的控制器的性能指标（超调量、上升时间、调整时间）非常接近参考模型而得到预定的性能指标，其他两种控制器的性能都与参考模型的预定性能指标有较大的差距，因此只有本文提出的控制器实现了预定性能要求。

表2 控制性能指标Tab.2 Control performance indicators

此外，为了对比本文所提出控制器的指定时间收敛性能，给出如表3 所示三种控制器三通道（t=10s时刻）的稳态跟踪误差、最大姿态角跟踪误差和收敛时间。

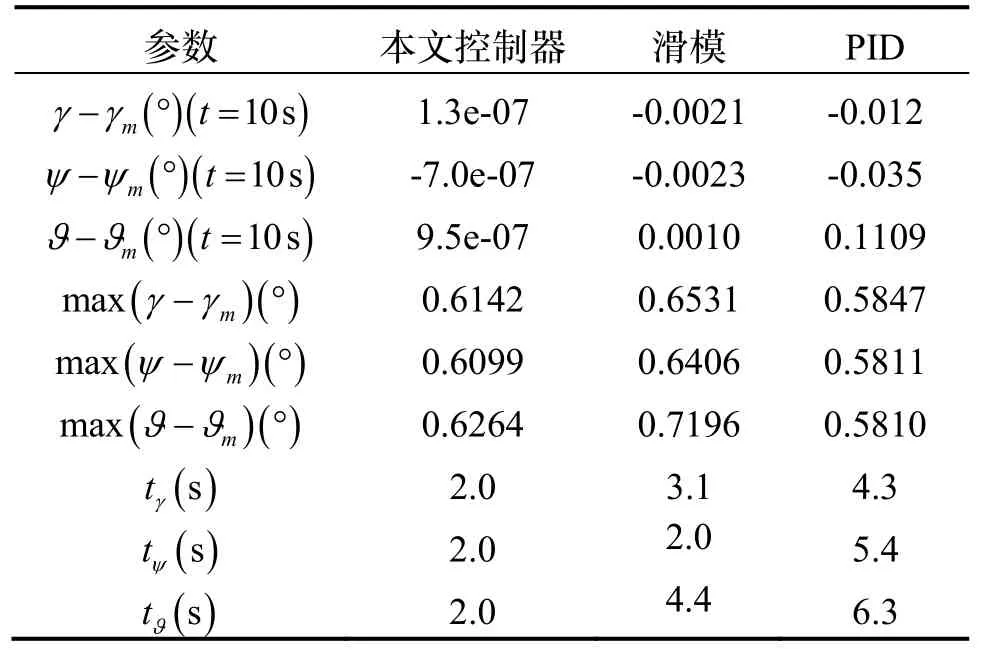
表3 三种不同控制器下的仿真结果Tab.3 Simulation results under three different controllers

通过对比滑模控制器、PID 控制器和本文提出控制器的数值仿真结果可知，三者均能在一定程度上跟踪期望参考模型，获得一定期望的超调量和响应时间，但是滑模控制器和PID 控制器的最终姿态角误差都比本文设计的控制器大，且不能保证指定时间的收敛性能。虽然PID 控制器的最大姿态角误差最小（在初始阶段），但会产生较大的超调量（如图3 所示）。相比之下，本文提出的控制器实现了更高的姿态控制精度（10-7度量级），且三通道的控制指令均是平滑且不饱和的。

3.2 不同指定收敛时间的控制仿真

为了验证所提出控制器的指定时间收敛性能，在控制器其他参数不变的条件下，参数TC分别设置为2 s、3 s、4 s 和5 s，以俯仰通道为例，得到的仿真结果如图5 所示，其他两个通道均具有类似结果，在此不再赘述。

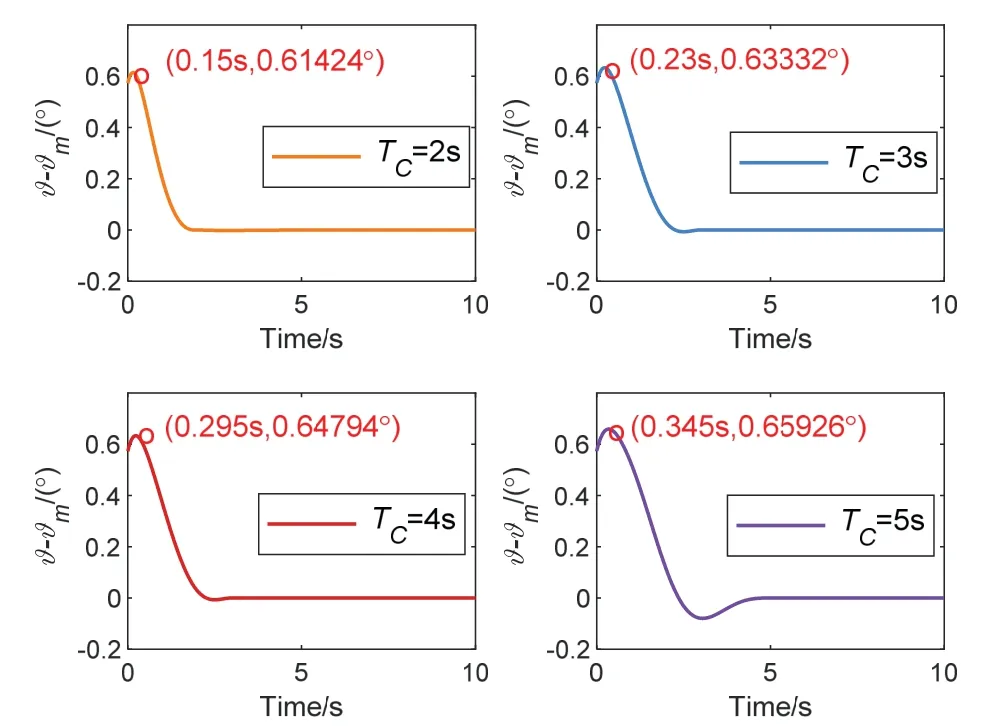
图5 俯仰通道姿态角跟踪误差Fig.5 Attitude tracking errors of pitch channel

由图5 可以看出，本文提出的控制器可以保证指定时间收敛的控制效果，实际收敛时间等于控制器设计参数，且控制的姿态角误差曲线均是平滑无抖振的，俯仰角的最大跟踪误差为0.65926 °。

3.3 仿真结果分析

通过特征点仿真，三种控制器都能在7s 内跟踪参考模型。但由于其他控制器的收敛时间与参数之间没有明确的关系，调整收敛时间需要复杂的调参过程，且另外两种控制器稳态误差分别为10-3和10-1量级，跟踪误差较大，所以未能很好的实现参考模型的指定性能。本文所提出的控制器在指定的时间收敛，误差收敛的过程平滑、收敛速度均匀没有突变，且稳态误差为10-7度量级，所以在产生更加平滑和不饱和的三通道控制指令的同时实现了最高精度的跟踪。

通过修改指定收敛时间，提出的控制器在指定的时间实现了高精度的控制。但收敛时间增加至5 s 乃至更大的情况下，由于李雅普诺夫函数有两项，所以姿态跟踪误差有一定的超调量，且存在一定的提前收敛情况，但不影响性能。

4 结论

本文针对捆绑运载火箭跟踪控制性能易受参数影响而不确定的问题，提出了一种控制性能指标可预先定制的姿态控制方法。基于参考模型、姿态跟踪误差动力学模型和指定时间收敛函数，使用反步法设计了一种能够实现参考模型预设的超调量为4.57%、上升时间为2.64 s 和调整时间为4.78 s 的指定时间收敛控制器。同时，控制器的收敛时间可以被定义为单一的控制参数，便于控制器设计。通过数学推导，证明了该控制器的全局稳定性和指定时间收敛性能。此外，单一特征点处的数值仿真结果表明，该控制器具有较高的精度（稳态误差小于10-6度）和较强的鲁棒性，在外部干扰下能够实现指定时间收敛，且相较于传统滑模控制器和PID 控制器，本文设计的控制器具有更好的动态性能和稳态性能。