考虑时间延迟的经纬仪测星评估惯导姿态误差方法

孔祥龙，刘程浩，周海渊，刘新明，孙伟强

（1.中国卫星海上测控部，江阴 214431；2.天津航海仪器研究所，天津 300131）

大型航天测量船是我国测控网的重要组成部分。测量船上搭载的测量设备一般采用单站定位体制且平台在运动，因此要想获得高精度的目标信息，船载惯性导航系统提供的姿态信息精度至关重要。

由于缺少更高精度的参考基准，动态条件下如何评估惯导系统姿态精度成为迫切解决的问题[1]。目前船载惯导动态姿态精度评估方法多基于天文测量，即利用卫星导航系统提供的位置和时间信息，通过恒星观测和天文解算得到惯导系统的姿态误差。李德彪等提出了一种基于多星同步检测定位定向技术的实时姿态测量方法[2]，介绍了基本的大视场多星定位定向原理和数学模型。理论分析表明，该方法具有较高的测量精度。潘良等提出一种利用经纬仪测星解算惯导姿态角误差方法：用多星短时（单星2 s）跟踪解算惯导姿态角误差稳态分量；用长时间（单星200 s 以上）跟踪特殊方位角的单颗恒星评估惯导姿态角误差的动态特性[3]。理论精度分析和实验表明，该方法具有较高的测量精度，为惯导系统动态姿态精度评估提供了一种有效手段。

随着技术的发展进步，惯导系统精度逐年提高，对姿态精度评估手段也提出了更高的要求。同时，激光陀螺捷联惯性导航系统（Strapdown Inertial Navigation System,SINS）已逐步取代传统的平台惯导系统成为多数应用领域的主流[4-10]。相较于平台惯导，SINS 具有体积小、重量轻、集成度高、精度更高等诸多优点。但由于激光陀螺的去抖滤波和解算延迟等原因，SINS 的输出带有较大的时间延迟，最大可能达到20 ms[11]。而上述惯导姿态误差评估方法中均未考虑此延迟的影响，导致动态条件下姿态评估精度较差。本文针对性提出了一种带有时间延迟估计和补偿的经纬仪测星评估惯导姿态误差方法，有效提高了惯导姿态误差动态评估精度。

1 经纬仪测星解算惯导姿态误差原理

1.1 坐标系及转换关系定义

惯导地平坐标系On-X nY n Zn：原点On为惯导的三轴交点，三轴分别指向北、天、东方向。恒星在On-X n Zn平面的投影与正北方向的夹角A为方位角，顺时针为正；视轴在水平面的投影与视轴的夹角E为大地高低角，向上为正。（A,E）确定恒星在惯导地平系下的位置。

惯导甲板坐标系On-X bY b Zb：原点On为惯导的三轴交点，三轴分别指向船体前、上、右方向。

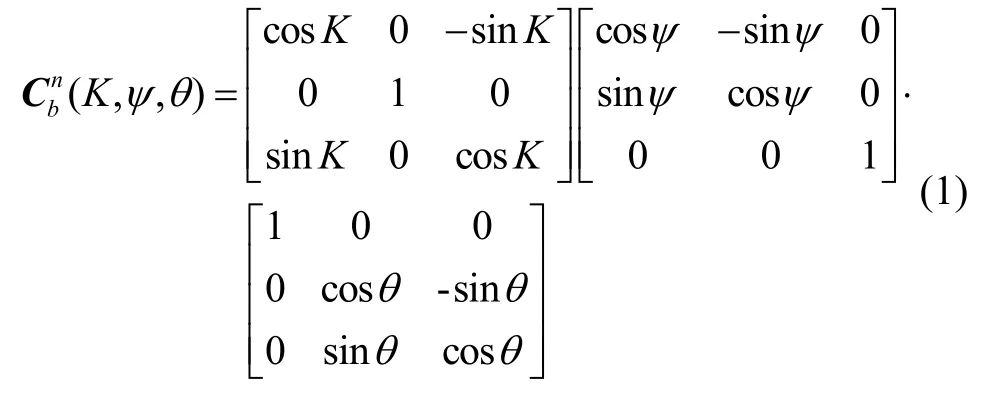
式中，K、ψ、θ分别表示船体航向角、纵摇角和横摇角。其中，航向角顺时针为正。

1.2 经纬仪观测与惯导姿态误差数学模型

根据卫星导航系统提供的船体位置、时间信息和系统内置星库中的赤经、赤纬、自行和周年视差等参数，经天文计算可精确得到星体在地平坐标系下的理论方位角A和高低角E。经纬仪对恒星实施观测，获取相对船体甲板坐标系的方位角Ac、高低角Ec等观测量。由于经纬仪测角精度很高，经轴系参数补偿后的实测值Ac、Ec也认为是准确的[3]。因此，有如下关系式成立：

将式(3)与式(2)做差并忽略二阶小量，可得：式中，Aω、Eω分别表示船体角速度引起视轴扰动角速度的方位、俯仰分量。

2 时间延迟估计及补偿

由式(7)(8)(9)可知，ΔA、ΔE实际包含两项，一个为短时间内不变项，另一个为时变项ΔAt、ΔEt。其中，主要受惯导姿态误差影响，一般小于20"；ΔAt、ΔEt与船体角速度及恒星位置相关，实际中时延10 ms 时此项可达角分量级，而文献[3]的方法中没有考虑此项。由于惯导系统与经纬仪系统刚性连接，两者间变形小于2"，可忽略变形对ΔA和ΔE的影响。

当观测多颗恒星时，可以获取多个观测量ΔAi、ΔEi（i=1,2...k），令：

3 仿真分析与试验验证

3.1 仿真分析

仿真条件：考虑船舶在三个轴上为正弦运动，横摇、纵摇、航向的幅值和摇摆周期分别设置为4 °、2 °、3 °和10 s、15 s、20 s。仿真时长80 s，采样频率为100 Hz。期间每40 s 跟踪一颗星，两颗恒星的理论大地角方位角和高低角分别设为[ 30°,40° ]和[120°,50°]，经纬仪测角误差设置为3"，惯导输出姿态误差角均设置为0，时间延迟分别设置为10 ms、20 ms。

图1 给出了10 ms 和20 ms 延迟时惯导计算星体大地角误差曲线。可以看出，星体跟踪过程中ΔA、ΔE有较大变化，20 ms 延迟下变化幅度接近200"。若不进行有效补偿，必然对姿态估计精度带来严重影响。

图1 存在时延时的惯导计算方位和高低角误差Fig.1 Azimuth and elevation errors calculated by SINS with time delay

为验证方法的有效性，使用文献[3]（表示为“Pan”）提出的方法和本文方法（表示为“Our”）进行解算与比较，具体对比如下：首先，从每颗星中40 s数据中随机抽取2 s 数据观测；然后，分别利用两种方法进行解算；重复以上过程50 次，并统计结果。

时延10 ms 和20 ms 的误差估计结果如图2-3 所示，时间延迟估计误差如图4 所示，图中横坐标“N”表示第N次解算结果。可见，本文方法能够有效估计时间延迟，估计误差最大值不超过0.5 ms。两种方法仿真结果比对如表1 所示。在10 ms 延迟下，Pan 方法的总姿态估计误差均值和标准差分别为5.12 ″和87.3 ″，本文方法的总姿态估计误差均值和标准差分别为0.14 ″和0.86 ″；在20 ms 延迟下，Pan 方法的总姿态估计误差均值和标准差分别为9.65 ″和162.96 ″，本文方法的总姿态估计误差均值和标准差分别为0.14 ″和1.95 ″。可以看出，由于参与解算星数比较少且惯导数据中存在较大时间延迟，Pan方法的总姿态估计误差已超出惯导本身精度，不再可用。而本文方法能够有效估计和补偿时间延迟的影响，在如此苛刻条件下也能得到高精度的估计结果，总的姿态估计误差小于2 ″。

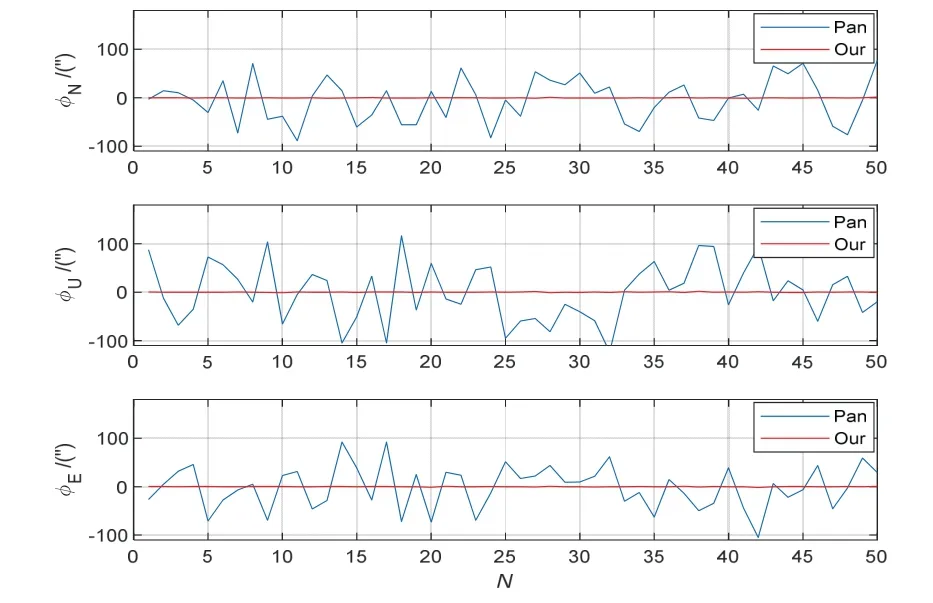
图2 时延10 ms 时不同方法仿真结果Fig.2 Simulation results of different methods with 10 ms time delay

图3 时延20 ms 时不同方法仿真结果Fig.3 Simulation results of different methods with 20 ms time delay

图4 时间延迟估计误差Fig.4 Estimation error of time delay

表1 不同方法仿真结果比对Tab.1 Simulation results of different methods

3.2 船载动态试验验证

为进一步检验本文方法的有效性，利用某测量船搭载的某型SINS 和某型光学经纬仪进行试验。设备安装关系如图5 所示。SINS 与经纬仪安装在同一吊桶，保证了设备间的刚性连接，试验前惯导与光学设备已在坞内进行坐标系取齐。试验选择在良好天气条件下进行，以便尽可能观测到更多恒星。

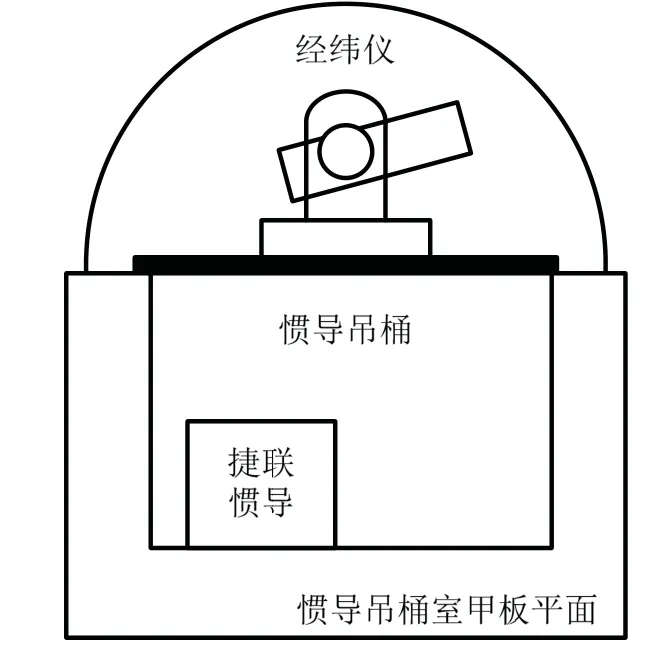
图5 设备安装示意图Fig.5 Equipment installation diagram

这里采用与仿真分析相同的方法进行估计精度对比：对单星进行长时间跟踪，跟踪时间为40 s。每次解算时随机从每颗星40 s 数据中抽取2 s 数据进行计算并统计结果，共进行50 次解算。

本次试验共跟踪16 颗星，所有跟踪恒星的大地方位角和高低角如图6 所示，惯导计算星体大地角误差如图7 所示。由于无法确知真实的惯导姿态误差，因此在比较方法估计精度时，以所有16 颗星、所有时长的跟踪数据利用本文方法解算的结果为惯导姿态误差真值。这样利用了所有可用的测量信息，可以认为是比较准确的“真值”。

图6 地平系下恒星方位角和高低角Fig.6 Azimuth and elevation angles of stars in horizon system

图7 惯导计算方位角和高低角误差Fig.7 Azimuth and elevation error calculated by SINS

为对比方法精度，分别用2 颗、8 颗和16 颗星参与解算，惯导平台失准角误差估计结果如图8-图10所示，时延误差估计结果如图11 所示，两种方法解算结果比对见表2。可见，Pan 方法在参与解算星数较少时总的估计误差较大，随着参与解算星数的增加，估计精度有所提高。Our 方法精度受参与解算星数的影响较小，在仅有2 颗星参与解算时总的姿态估计误差均值小于7 ″,标准差小于13 ″，因此在天气不佳测星数较少时仍能得到较好的估计精度，提高了方法的可用性。同时，在2 颗星、8 颗星和16 颗星参与解算情况下，Our 方法的估计精度（总姿态估计误差标准差）相较Pan 方法分别提升75%、78%和81%，平均提升约78%。

表2 不同方法解算结果比对Tab.2 Results of different methods

图8 2 颗恒星参与解算时的结果Fig.8 Results of two stars participating in the calculation

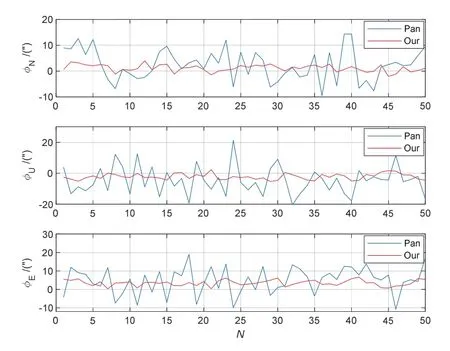
图9 8 颗恒星参与解算时的结果Fig.9 Results of eight stars participating in the calculation

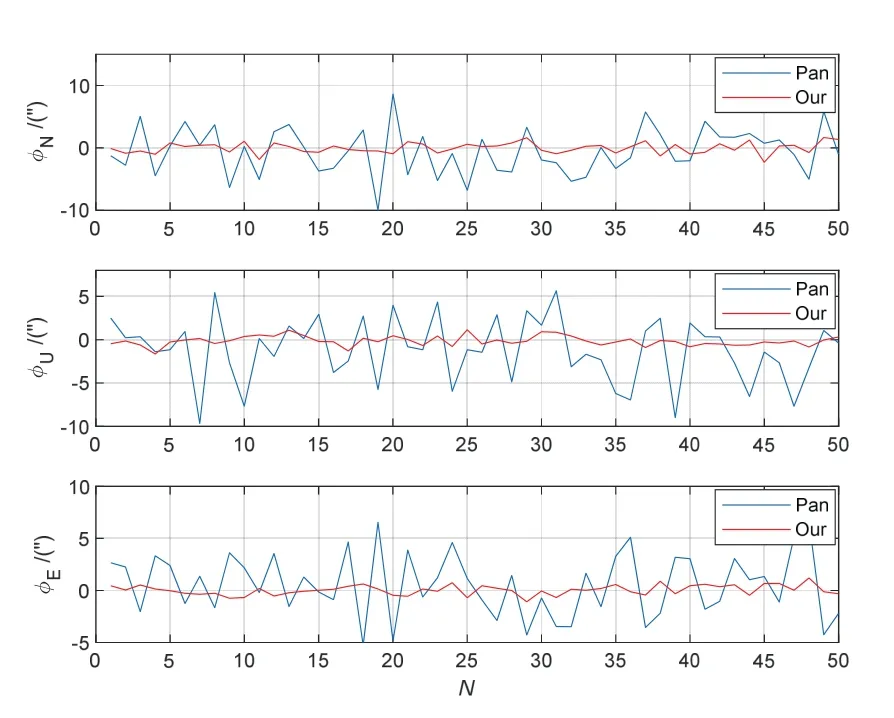
图10 16 颗恒星参与解算时的结果Fig.10 Results of sixteen stars participating in the calculation

图11 时间延迟估计误差Fig.11 Estimation error of time delay

4 结论

本文针对性提出了一种带有时间延迟估计和补偿的经纬仪测星评估惯导姿态误差方法，推导了经纬仪观测量与惯导输出姿态误差和时间延迟的数学关系，建立了时间延迟估计和补偿模型。仿真分析表明，在观测星数较少且惯导数据中存在较大时间延迟时，现有方法在动态条件下的姿态估计误差可能超出惯导本身精度，不再可用。而本文方法能够有效估计和补偿时间延迟的影响，在时延20 ms 且只有2 颗星可观测条件下，也能得到高精度的估计结果，总姿态估计误差小于2 ″。船载动态试验表明，该方法相比于现有方法平均估计精度提升约78%。