Geogebra软件在波动光学教学中的应用

罗宇晴，吴少平

华中师范大学物理科学与技术学院，武汉 430079

光学是物理学一个重要的学科分支，光的干涉和衍射现象是光学重要的研究内容。1801年，托马斯·杨用光的“波动性”解释了光的干涉现象，第一次成功测定了光的波长。1815年，菲涅尔对惠更斯原理进行了修正，提出了惠更斯-菲涅尔原理。该原理不仅能解释各向同性均匀介质中光的直线传播现象，还完美地解释了光的衍射现象[1]。从此，波动光学发展成为光学的重要组成部分。由于观测光的干涉和衍射现象对实验条件要求较高，教师难以在课堂进行演示实验。2016年，教育部印发的《教育信息化“十三五”规划》提出要创新应用优质教育资源，积极探究新型教学模式[2]。Geogebra是一款结合几何、代数、微积分和统计功能的动态数学软件[3]，该软件开源免费，简单易学，而且交互性好，特别适用于理科教学[4]。笔者利用Geogebra软件制作动态演示图，用于波动光学中2个典型实验的理论教学。

1 利用Geogebra演示双缝干涉实验

1801年，英国物理学家托马斯·杨利用双缝实验演示了双光束干涉现象，并首次推算得到光的波长，实验验证了光的波动理论，为量子学说的创立奠定了坚实的基础。两列频率相同、振动方向相同，并且在观察期间相位差不变的相干波叠加后，合振动会在某些区域加强，而在某些区域减弱。叠加区域内各点合振动强度在空间中的稳定非均匀分布即为光的干涉图样，其本质为两列光波相位差的空间分布。在传统课堂教学中，通常用光线代替光波，无法直观展现出相位差的变化。利用Geogebra软件，不仅可以直观展示相位差的大小，还可以清晰地观察到狭缝间距和入射光振幅变化对光强分布的影响，从而帮助学生深入理解双光束干涉的物理机制。

1.1 双缝干涉理论知识

如图1所示，两列等振幅且初相位相同的相干波分别从空气中的定点A和B出发到达空间P点，两列波的振动方程可分别表示如下：

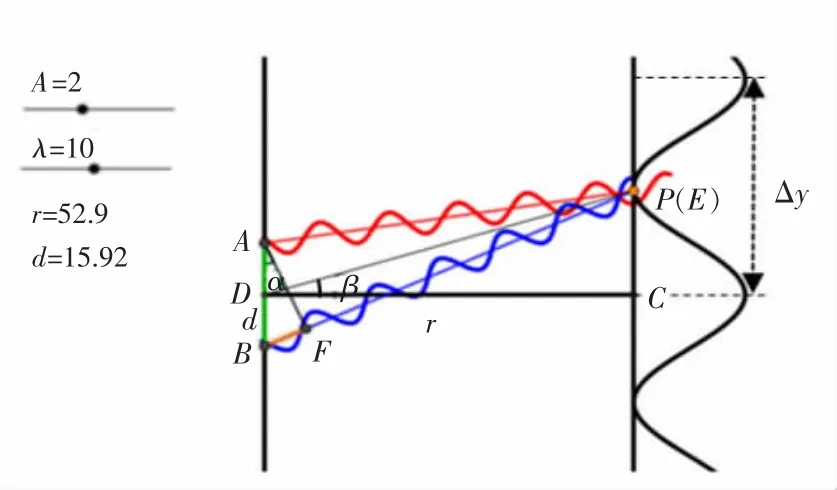
图1 双缝干涉动态图

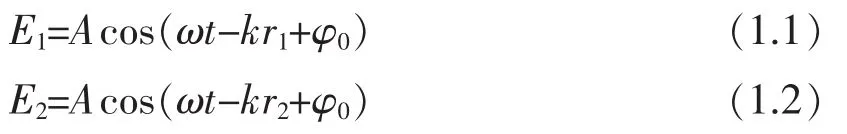
式中E1和E2表示电场强度，ω为角频率，波数，λ 为波长，r1＝AP，r2＝BP，φ0为初相位。两列波在 P 点相遇后的相位差 Δφ＝k（r2-r1）＝kδr,其中δr表示光程差，空气中折射率n≈1。

当光程差等于半波长的偶数倍，两列波叠加后的强度为最大值，形成亮纹，称为干涉相长；

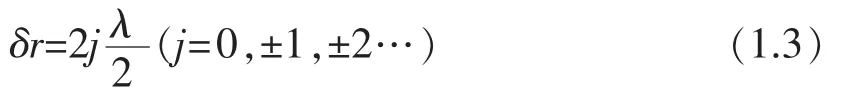
当光程差等于半波长的奇数倍，两波叠加后的强度为最小值，形成暗纹，称为干涉相消。

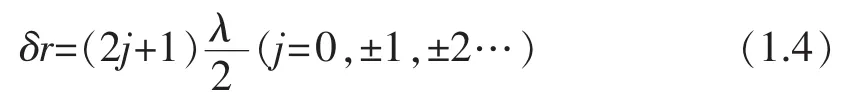
上式中j表示干涉级，从0级开始计算。

由图1可知，光程差可以表示为：

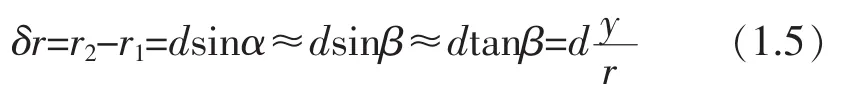
（1.5）式中 d＝AB，表示双缝之间的距离，r＝CD，y＝CP。

将（1.5）式代入（1.3）式，得到产生明纹的条件为

将（1.5）式代入（1.4）式，得到产生暗纹的条件为

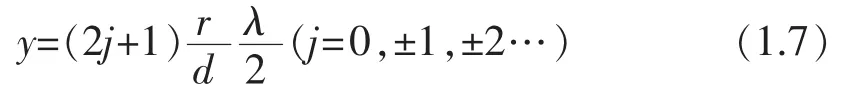
相邻两条明纹或相邻两条暗纹之间是等间距的，间距Δy的大小为

1.2 课件制作

（1）双缝制作过程

如图1所示，两束相干光通过狭缝A与狭缝B会聚在光屏上P点。用描点工具单击y轴，设定点 A，然后在命令栏输入 B（0,-y（A））。

（2）光屏制作过程

用描点工具单击x轴正半轴，设定点C；单击原点，设定点D。用垂线工具单击点C与x轴，创建直线f来模拟光屏。在直线f上任取一点P，利用线段工具分别单击点A与点P创建线段AP，单击点B与点P创建线段BP，单击点D与点P创建线段DP。

（3）参数制作过程

创建波动方程中的4个参数，即振幅A、波长λ、波速v和时间t。为确保干涉现象全参数可调，利用滑动条工具单击绘图区，创建振幅A，设置变化范围[0.1，5]，单位为 V/m；创建波长 λ，设置变化范围[0.2，15]，单位为 μm；创建波速 v，设置变化范围[0.1，5]，单位为 m/s；创建时间 t，设置变化范围[0，25]，单位为s。点击右键设置动画属性为“重复递增”。

（4）波动方程制作过程

在命令栏输入 p（x）＝if（0＜x＜Length（DP）＋1，Asin（2π（vt-x）/λ）），得到一列沿 x 轴传播的波函数。在命令栏输入 Rotate（p（x），atand（（y（A）-y（P））/（x（A）-x（P）））），得到曲线 a。在命令栏再次输入Translate（a，Vector（D，A）），我们就绘制出了第一列入射波。同理，绘制第二列入射波。

（5）光强分布函数制作过程

利用线段工具单击点A与点B，创建线段AB，单位为mm；单击点C与点D，创建线段CD，单位为m。在命令栏输入 q（x）＝2A2（1＋cos（2πdx/（λr））），创建光强分布函数，最后绘制出光强分布图。

（6）光强振幅制作过程

在命令栏输入 d＝p（Length（BP））＋p（Length（AP）），回车后继续输入 E（x（p），y（p）＋d），连接点P与点E，创建线段PE表示P点光强的大小，如图1所示。

（7）光程差制作过程

利用垂线工具单击点A与直线BP，创建垂线AF，垂线AF与直线BP交点为点F，线段BF即为光程差 δr。

1.3 课件说明

（1）改变两列相干波相位差的大小，分析明暗条纹产生的条件。

设置相关参数后，拖动点P在光屏上滑动，改变两列相干波相位差的大小。可以发现，当光程差相差半个波长的偶数倍，产生明纹（图2）；当光程差相差半个波长的奇数倍，产生暗纹（图3）。动画演示结果与（1.3）和（1.4）式结果完全一致。

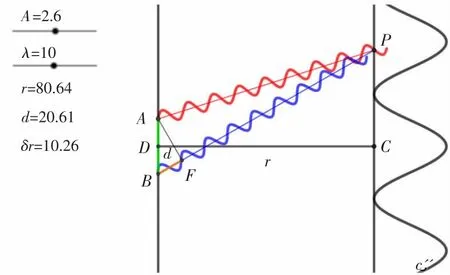
图 2 δr≈λ，P点为明纹

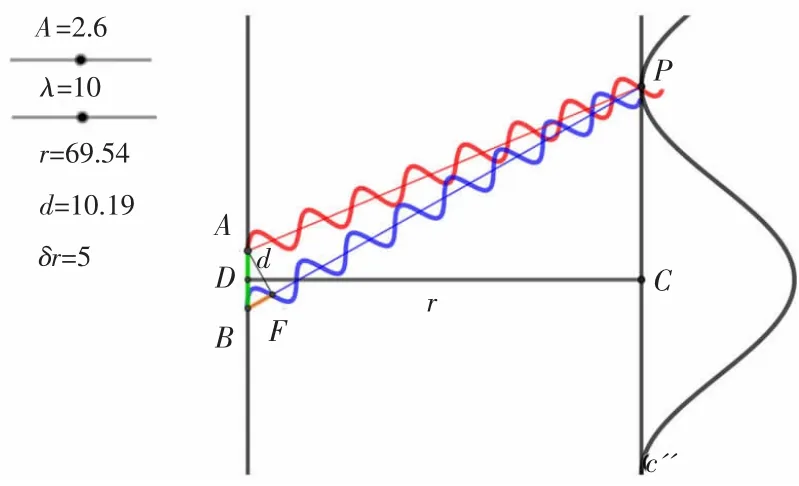
图 3 δr≈λ ／2，P 点为暗纹

（2）验证“r>>d时，∠α与∠β近似相等”的条件。

在推导光程差δr的过程中，当r>>d时，我们认为∠α与∠β近似相等。利用Geogebra软件，可以直观地证明这一条件的正确性。如图4所示，r≈3d时，∠α与∠β相差还比较明显；但当r与d取值相差很大（r≈30d）时，∠α与∠β几乎相等，如图5所示。

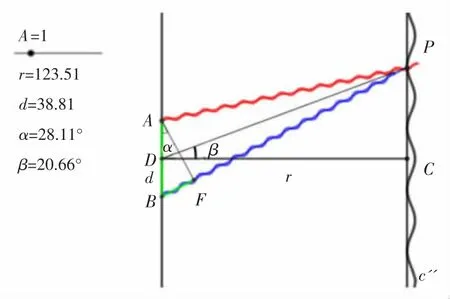
图 4 r≈3d 时，∠α≠∠β（X 轴∶Y 轴＝1∶1）

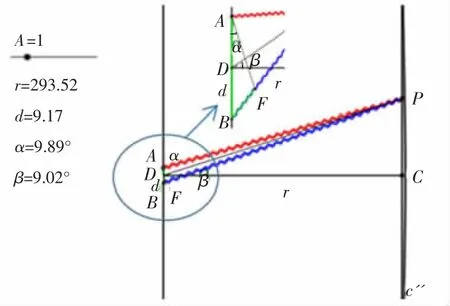
图 5 r≈30d 时，∠α≈∠β（X 轴∶Y 轴＝2∶1）

（3）改变双缝间距d，波长λ以及双缝到光屏的距离r，观察干涉图样的变化。

设置入射光振幅A为2.6 V/m，波长λ为10μm，r为65.88 m，拉动滑动条改变双缝间距d。对比图6和图7可以发现，随着双缝间距d增大，干涉条纹间距明显减小，与(1.8)式结果一致。设置r为65.88 m，双缝间距d为29.93 mm，拉动滑动条改变双缝到光屏的距离r。对比图7和图8可以发现，随着距离r的增大，条纹间距增大。拉动滑动条改变波长λ，对比图8和图9可以发现，随着波长λ的增大，条纹间距也增大。

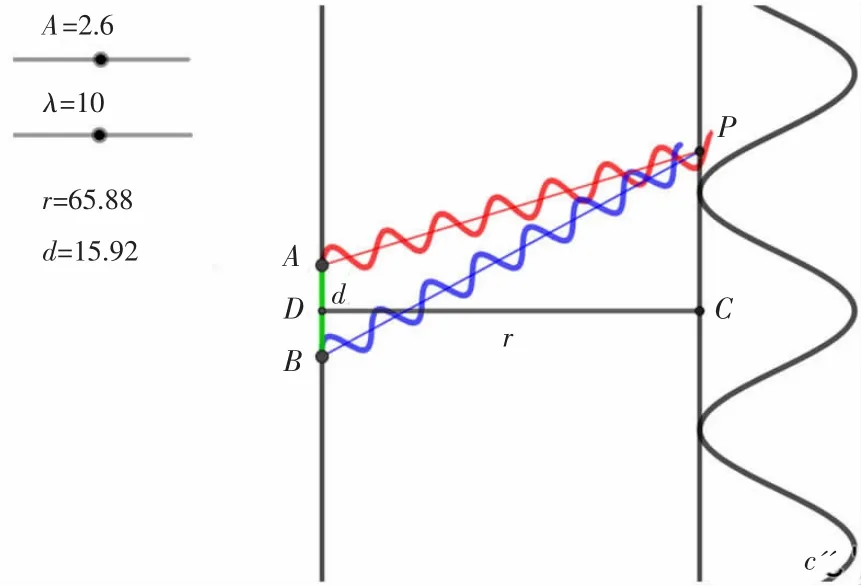
图6 d≈16时的双缝干涉图样

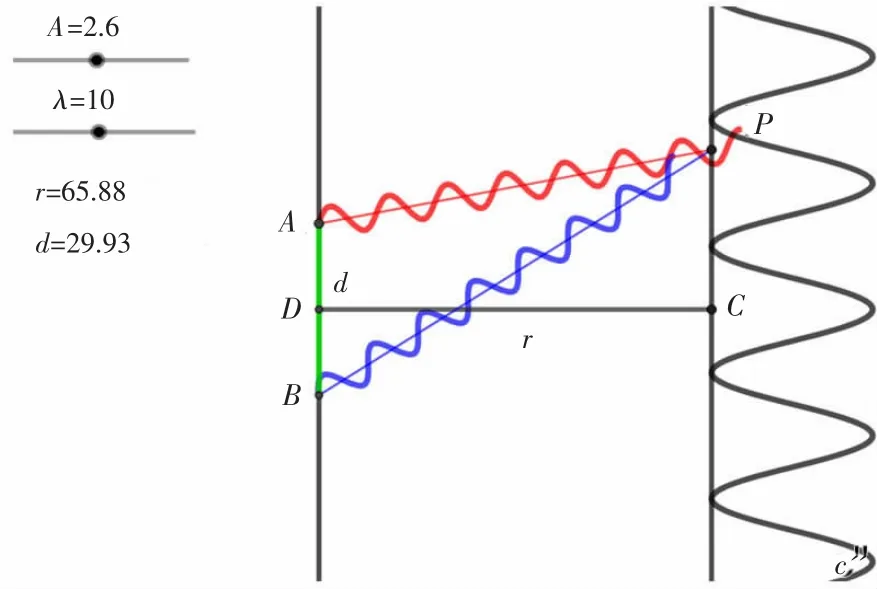
图7 d≈30时的双缝干涉图样

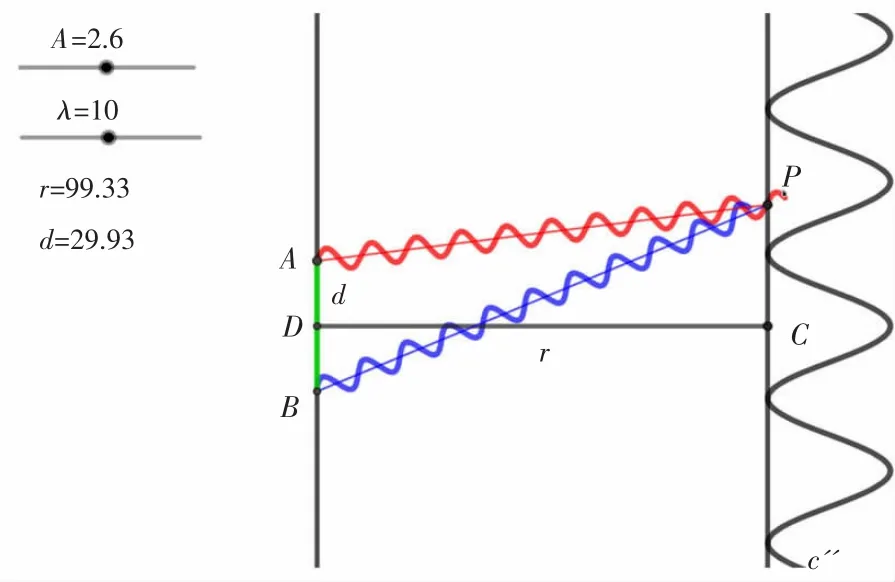
图8 λ=10时的双缝干涉图样

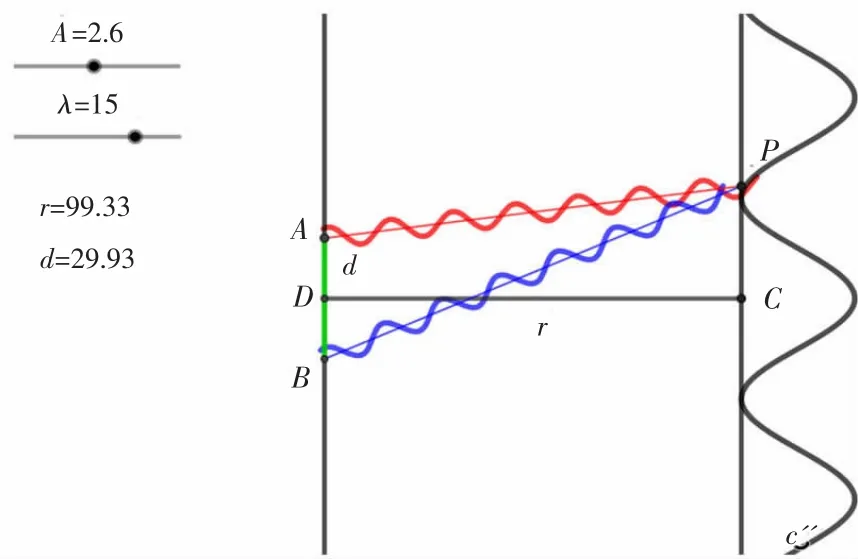
图9 λ=15时的双缝干涉图样

（4）改变入射波振幅，观察干涉图样的变化。

设置波长 λ 为 15 μm，r为 65.88 m，双缝间距d为29.93 mm，拉动滑动条改变入射光振幅A。对比图10和图11可以发现，随着入射光振幅A的增大，条纹间距不变，干涉光叠加振幅增大。

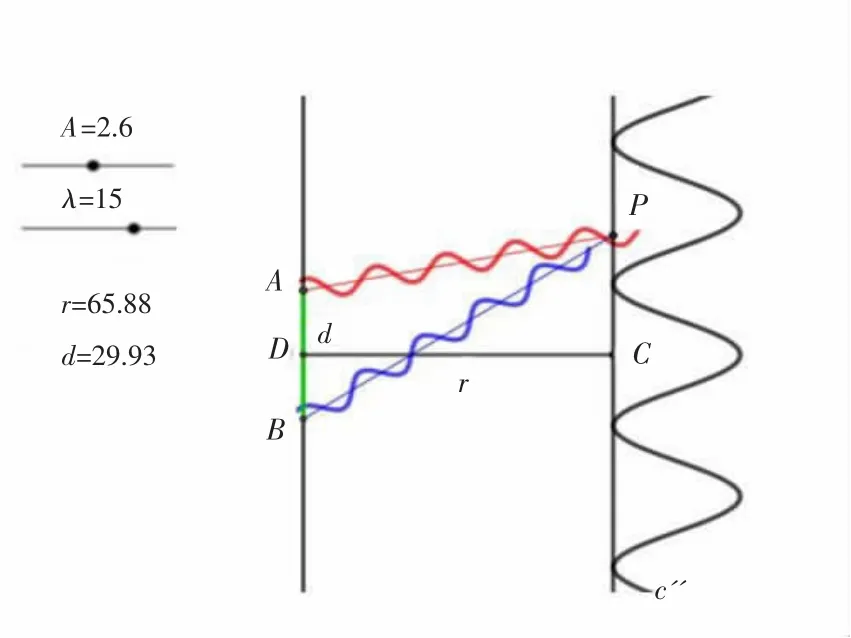
图 10 A＝2.6时的双缝干涉图样

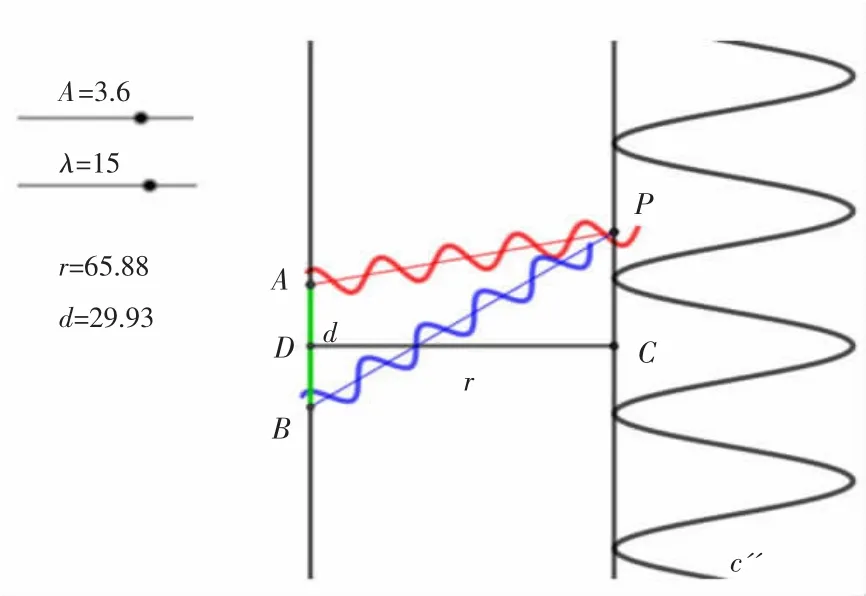
图 11 A＝3.6时的双缝干涉图样

2 利用Geogebra演示光栅衍射现象

“衍”始见于商代甲骨文，本指水流顺河道汇于海，引申指蔓延、扩展。光的衍射指光在空间传播过程中，遇到与波长差不多数量级的障碍物或者孔隙时，会发生光线弥漫的现象。由于可见光波长较短，光波的衍射现象在日常生活中并不明显。

2.1 理论知识

任何具有空间周期性的衍射屏都可以叫作光栅，衍射光栅一般每毫米内有几十条乃至上千条缝。光栅和棱镜一样，作为重要的分光装置，常用来形成光谱[1]。光栅衍射的光强分布是单缝衍射与多缝干涉共同作用的结果。利用矢量叠加的方法可以得到如下公式：

单缝衍射屏上P点光强公式：

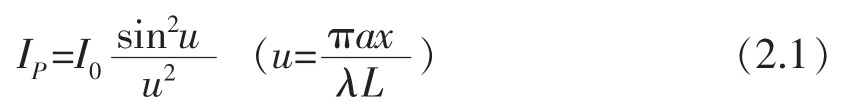
光栅衍射屏上P点光强公式：

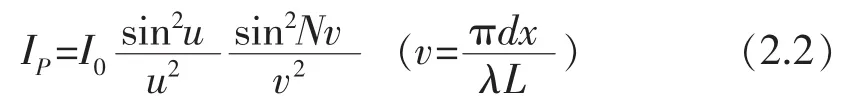
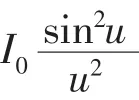
单缝衍射最小值位置满足条件：

多缝干涉主最大位置满足条件：

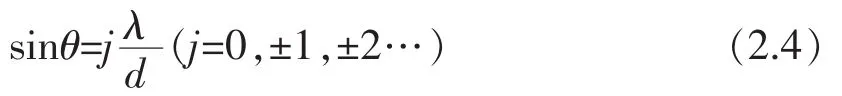
多缝干涉最小值位置满足条件：

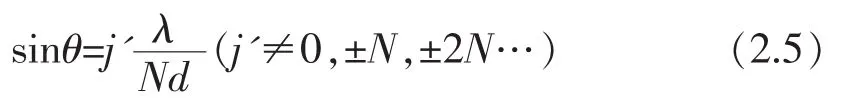
光栅衍射光强分布中的单缝衍射因子与单缝衍射强度曲线形式相同；光栅衍射图样中出现的一系列较强的亮线叫作主最大，较弱的亮线叫作次最大；相邻主最大之间有N-1条暗纹和N-2个次最大；主最大的宽度随N的增大而减小，且强度正比于N2。

2.2 课件制作

（1）参数制作过程

为确保单缝衍射光强分布全参数可调，利用滑动条工具单击绘图区。创建振幅A，设置变化范围[0，5]，单位为 V/m；创建波长 λ，设置变化范围[1，10]，单位为 μm；创建单缝宽度 a，设置变化范围[0，10]，单位为μm；创建光栅到光屏的距离参数 L，设置变化范围[0，10]，单位为 m；创建光栅缝数N，变化范围[1,100]，增量为1；创建光栅常数d，变化范围[1,30]，单位为μm。

（2）光强分布函数制作过程

在命令栏输入 f（x）＝A2sin2（πax/（λL））/（πax/（λL））2，表示单缝衍射光强分布函数。在命令栏输入 g（x）＝sin2（Nπdx/（λL））/sin2（πdx/（λL）），表示缝间干涉叠加效果；创建函数 h（x）＝f（x）g（x）／N2，表示光栅衍射光强分布函数。

2.3 课件说明

（1）改变狭缝宽度a，分析衍射图样的变化。

设置入射光振幅A为1V/m，距离L为1m，波长λ为4 μm，光栅常数d为18 μm，狭缝数目N为6。拖动滑动条，改变狭缝宽度a。对比图12和图13可知，在一定范围内，随着单缝宽度a增大，衍射效果对多缝干涉调制的效果越明显。如图13所示，当d=3a时，在±3λ/d主极大处出现了缺级。

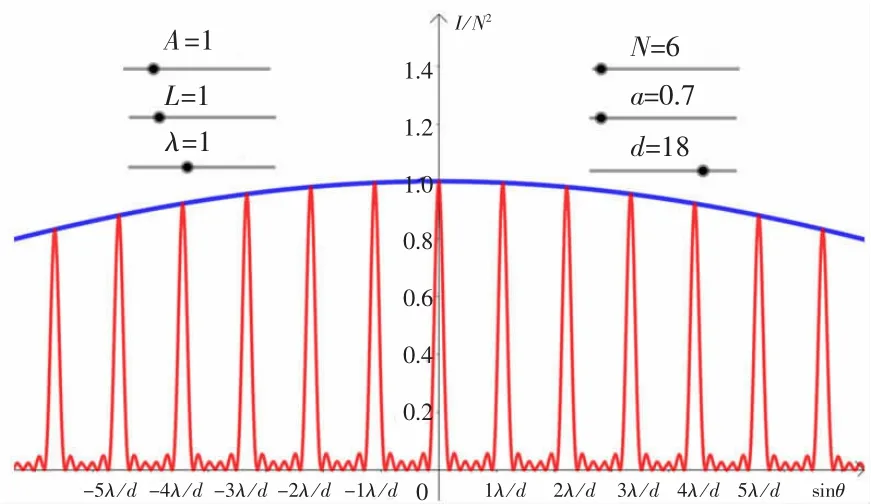
图12 狭缝宽度a=0.7时的光栅衍射光强分布图

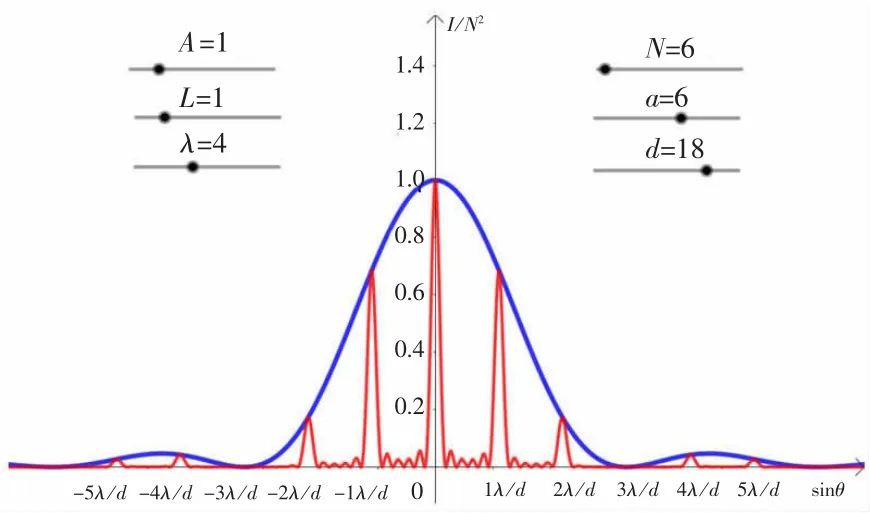
图13 狭缝宽度a=6时的光栅衍射光强分布图

（2）改变光栅常数d，分析衍射图样的变化。

设置入射光束振幅A为1V/m，距离L为1m，波长 λ 为 4 μm，狭缝宽度 a为 5 μm，狭缝数目N为6。拖动滑动条，改变光栅常数d，由图14与图15可知，在一定范围内，随着光栅常数d的增大，多缝干涉明纹(主极大)间距减小，与上文中双缝干涉得到的结论一致。如图14所示，当d=2a时，在±2λ/d主极大处出现了缺级。如图15所示，当d=4a时，在±4λ/d主极大处出现了缺级。

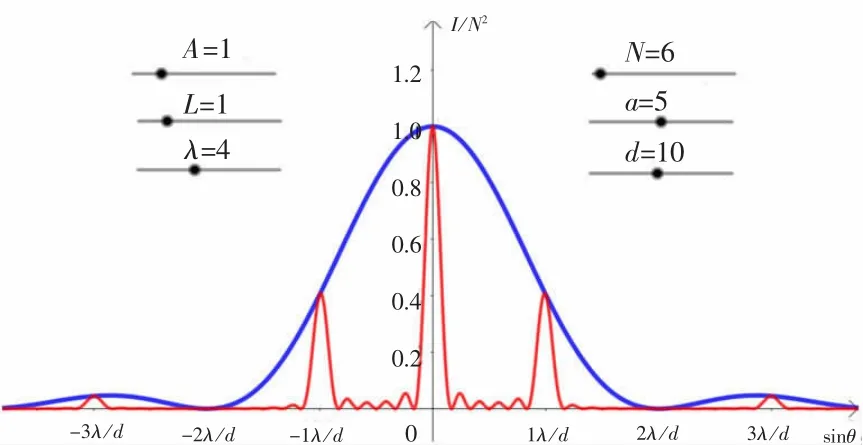
图14 d=2a时的光栅衍射光强分布图

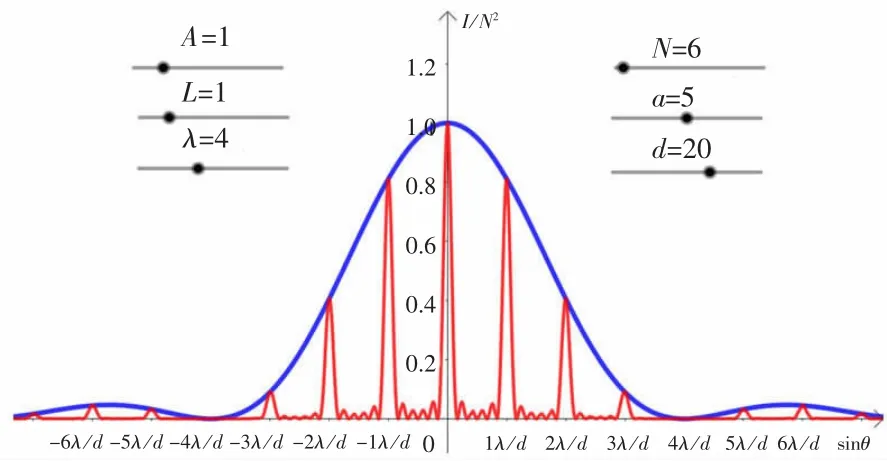
图15 d=4a时光栅衍射光强分布图

（3）改变狭缝数目N，分析衍射图样的变化。

设置入射光束振幅A为1V/m，距离L为1m，波长 λ 为 4 μm，狭缝宽度 a为 3 μm，光栅常数d为12 μm；拖动滑动条，改变狭缝数目N。对比图16与图17可知，随着狭缝数目N增大，衍射明纹变细变亮。d=4a时，在±4λ/d主极大处出现了缺级。

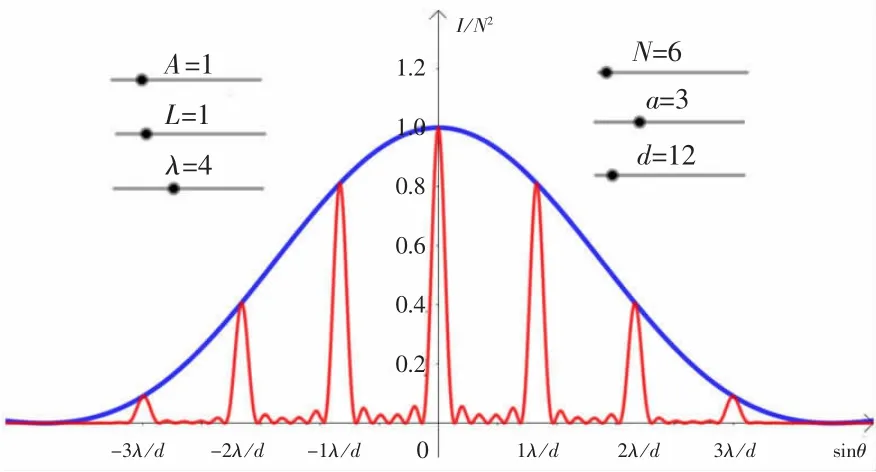
图16 N=6时的光栅衍射光强分布图

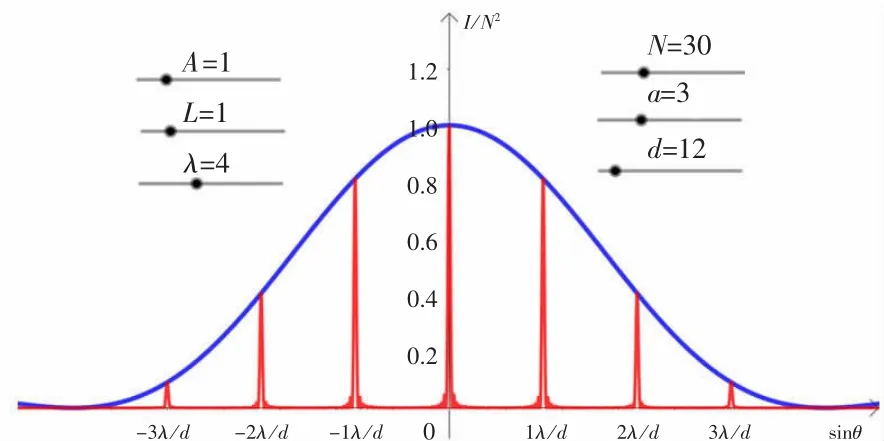
图17 N=30时的光栅衍射光强分布图

3 结论

将Geogebra软件用于波动光学教学有以下三个优势：一是可以生动形象地动态演示光的干涉、衍射现象，利于学生将抽象的物理知识转化为直观感性的认识；二是实现了实验过程全参数可调，可以让学生自主探究各物理量对光强分布的影响，充分调动了学生的主观能动性；三是有利于调动学生学习的积极性，培养学生自主探索和自主学习的科学素养。