从科学推理的角度重构教学逻辑——以“浮力”一课为例

刘 旭

首都师范大学附属苹果园中学分校，北京 100144

物理课程核心素养中指出“科学思维是分析综合、推理论证等方法在科学领域的具体运用”[1]，科学推理是其要素之一。演绎和归纳是两种常见的推理方式，在物理教学中，利用公式推导和探究实验得出结论分别是演绎推理和归纳推理的运用。公式推导是一种利用一定背景知识和数学手段演绎推理出其他结论的方法，课堂上合理运用公式推导，可以使学生将所学知识建立起关联，但在公式推导时若忽视了其中的逻辑要素，物理课堂就会流于数学计算，学生的科学思维素养难以得到提升。科学探究也是物理课程核心素养之一，但探究实验也包括了从实验现象中归纳得出结论的过程，仍需进行严谨的推理，所以其中也有科学思维素养的成分，不重视思维过程的探究实验，最终会演变成“假探究”。

1 传统教学中的推理过程

“决定浮力大小的因素”和“阿基米德原理”是与浮力有关的两部分重点教学内容，不同版本教材或安排在同一节中，或安排了两节，本文中的“浮力”一课同时包含了以上二者。在传统教学中，“决定浮力大小的因素”和“阿基米德原理”两条结论的得出，都分别运用了两种推理方式——基于归纳推理的探究实验和基于演绎推理的公式推导。两种推理方式所得结论互相印证，使得结论的得出过程更具有科学性。但站在科学推理的角度，其中一些问题仍需引起重视。

1.1 基于归纳的结论得出

在探究实验中处理多变量问题时，常采用控制变量法进行实验。而需要对哪些变量进行控制，是切实需要解决的问题，形成合理的猜想在实验中就显得尤为重要。在探究“影响浮力大小的因素”时，人教版教材就指出了“研究浮力与深度的关系时，要保证浸入液体中物体的体积不变”，这样图1中甲、乙两实验就不满足控制变量的要求，只能选用乙、丙两实验进行对比。但学生猜想可能影响浮力的因素时，不容易想到“物体浸在液体中的体积”这个物理量，因为学生不存在对“物体浸在液体中的体积”这个概念的认识，在常规教学中常常被已知结论的教师刻意“引导”出来。一个人的背景知识会影响到他的观察结果[2]，如果让学生经历真正的科学探究过程，就很容易从图1的甲、乙两实验中得出错误的结论。

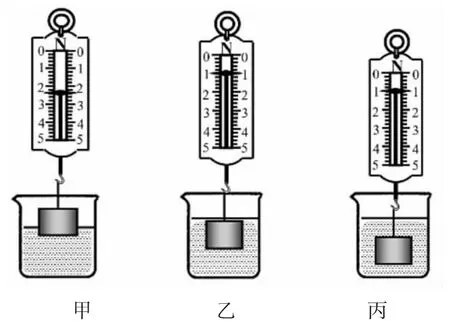
图1 探究浮力影响因素

同理，为了得到阿基米德原理，学生需要探究“浮力的大小跟排开液体所受重力大小的关系”，而该实验对变量的猜想更为困难，这就要求学生在进行实验之前已经在一定程度上认识到了阿基米德原理。

想要归纳得出“决定浮力大小的因素”和“阿基米德原理”两个实验的结论，就需要在实验前拥有相关的背景知识，这样实验也会更加偏向于验证性实验[3]。课标中指出了“注重科学探究，倡导教学方式多样化”的课程理念，鼓励教学中根据实际情况灵活选用教学方式[1]。笔者认为，与其教师刻意地“引导”学生猜想出相关变量，不如干脆将这两个实验改为验证性实验。

1.2 基于演绎的结论得出

在传统教学中，教师首先会指出浮力产生的原因，并选取一个长方体模型进行分析。如图2所示，首先可得到 F浮＝F向上-F向下，然后推导得出计算公式 F浮＝ρ液gV排（一般称之为“阿基米德原理推论”，下文简称“浮力公式”），再推导得出阿基米德原理 F浮＝G排液。

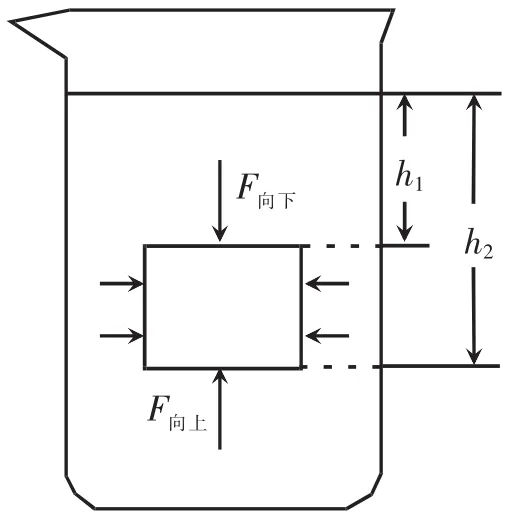
图2 用长方体模型推导阿基米德原理

综上，当试图通过探究实验得出结论时，就需要教师对学生进行刻意的“引导”，容易演变成“假探究”；当试图通过公式推导得出结论时，初中学生数学水平的限制又会使得出结论的过程缺失普遍性，只能依赖于教师的补充说明。因此，想要学生的科学思维素养在“浮力”一课中有所提升，就需要教师妥善处理本课中各部分教学内容，以及公式推导与实验之间的关系。

2 利用等效思想得出阿基米德原理

2.1 阿基米德的证明过程

当知道浮力的产生原因后，阿基米德原理可以由此推导得出。但在阿基米德的时代，人们的科学认识以及数学水平不足以掌握这种推导方法，因而阿基米德本人采用了另一种证明方法。既然初中生的数学水平有限，那么模仿阿基米德的证明方法就是一种相对合理的教学方式，而利用一种不具有普遍性的模型进行推导就显得不必要了。阿基米德在他的著作《论浮体（卷I）》中，通过对命题5—命题7三个命题的证明，分别讨论了处于不同状态的物体所受浮力大小，而将三个命题综合成一条规律就是如今的阿基米德原理[4]。因古希腊时期的科学概念与现今存在一定区别，且阿基米德原文主要探讨的是不同情况下物体表观重力大小的变化，而本文意在梳理阿基米德原理的证明过程，故仅从笔者个人理解的角度予以介绍，原文见文献[4]。

阿基米德的命题5对漂浮的物体所受浮力等于它排开液体所受的重力大小进行了证明。如图3所示，液体左侧漂浮一物体，物体对液体施加的压力大小等于它受到的浮力大小，在液体右侧截取与物体浸入液体部分相同体积的液体，这部分液体对其他液体施加的压力大小等于它受到的重力大小。又因物体下方的液体并未流动，故液体两侧所受的压力大小相等，于是证明了漂浮的物体所受浮力大小等于它排开液体所受的重力大小。

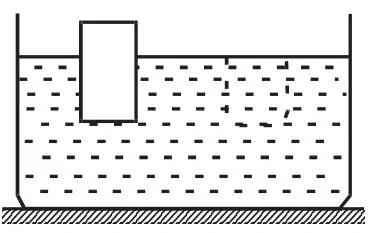
图3 阿基米德原始推理

然后以命题5为基础，在命题6和命题7中分别证明了受迫浸没于液体中的物体、沉底的物体所受浮力大小也等于物体排开液体所受的重力大小。

阿基米德的推理过程非常精彩，但由于时代的局限性，阿基米德原理需要拆分成三个命题进行证明，过程相对复杂。阿基米德在原著中将浮力描述为重量差，他并没有把浮力当作一种力来看待，就不会理解相互作用力的关系（牛顿第三定律），因而没有意识到物体无论处于何种状态，物体对液体的压力大小永远与其所受浮力大小相等，所以不必用三个命题分别对不同种状态的物体进行分析。

但同时，我们可以在阿基米德的推理过程中挖掘他的深刻思想，命题5是后续两个命题得以证明的基础，而命题5的证明过程运用了等效思想，他发现了物体对液体的压力和液体对液体的压力是等效的，所以液体才不会流动。虽然课堂上不宜复现阿基米德相对复杂的证明过程，但可保留他的等效思想，再结合学生的已有知识，设计出一种新的推理出阿基米德原理的方法。

2.2 改进的推理方法

为了降低学生理解等效思想的难度，教师可展示一个学生利用已有知识能够解决的典型问题作为引入。如图4所示，甲、乙两个相同的柱形容器中盛有同种液体，将其放置在水平面上，在甲容器中放置一物体A，使得甲、乙两容器中液面处于同一高度h。因为甲容器中物体A受到了液体的浮力，力的作用是相互的，故物体A对液体也施加了一个与浮力大小相等、方向相反的压力F压，而乙容器中不存在物体A对液体的压力，但比甲容器中多了与物体A同等体积的液体。两容器底所受压强均为p＝ρ液gh。再根据F＝pS可知两容器底部所受液体压力相等，故两容器底部对液体的支持力相等，F支甲＝F支乙。再分别对甲、乙容器中的液体进行受力分析，可得到

又写作“笼罗”。《晋书·刘元海载记》：“及元海僣号，人谓元达曰，‘往刘公相屈，君蔑而不顾，今称号龙飞，君其惧乎？’元达曰，‘彼人姿度卓荦，有笼罗宇宙之志，吾固知之久矣。’”又写作“笼落”。《说文·竹部》：“笯，鸟笼也。”《楚辞·九章》：“凤皇在笯兮。王逸注云，‘笯，笼落也。’”《方言》：“笯，笼，南楚江沔之闲谓之篣。”以上“笼络”“笼罗”“笼落”皆有“包罗、覆盖”之义。

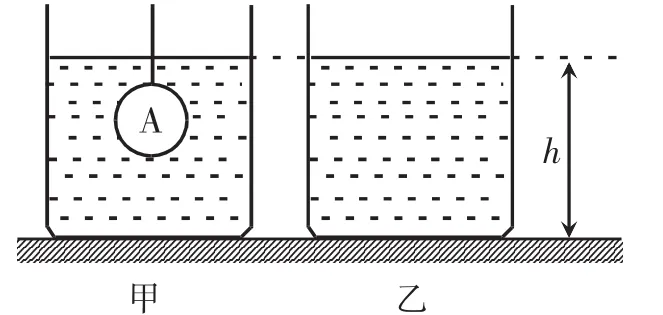
图4 改进的推理方法

F支甲＝G液甲＋F压

F支乙＝G液乙

综合两式可知，F压＝ G液乙-G液甲，物体 A 对液体的压力大小与物体A同等体积的液体所受的重力大小是相等的，故F浮＝F压＝G排液。这就说明，对于容器底的影响上，物体A对液体的压力与物体A排开液体所受重力是等效的，从而使学生初步感受等效思想。

但图4并非一种具有普遍性的模型，要想得到一种具有普遍性的阿基米德原理，仍然需要将等效思想应用到更一般的情境之中。如图5所示，只要保证液面高度不变，对于任意液体内部的任意一点M，其压强大小永远为p＝ρ液gh，与有无物体A无关。于是，推理的情境得以扩展，对于液体来说，物体A对液体的压力永远与物体A排开液体所受的重力是等效的，从而得到了阿基米德原理。如此进行推理，除了确保了推理过程的普遍性，还可以降低学生对“物体排开液体体积”的理解难度，为后续教学提供便利。

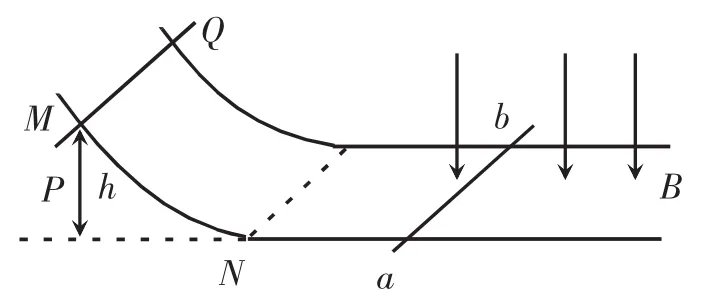
图4 平行弯曲导轨上的双导体棒

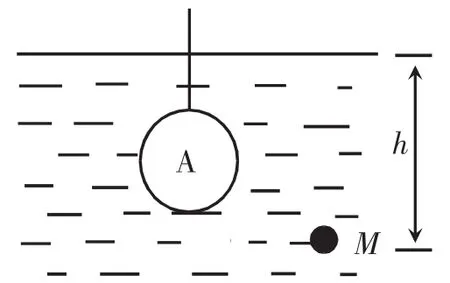
图5 扩展推理情境

3 重构“浮力”一课教学逻辑

既然阿基米德原理可以不由浮力公式推出，那么该公式就可以作为阿基米德原理的推论存在，探究实验也可以转变为验证性实验，“浮力”一课的教学逻辑得以重构。“浮力”一课主要包括结论类的内容：浮力的存在，浮力的产生原因，阿基米德原理，浮力公式；实验类的内容：测量浮力，探究影响浮力大小的因素，探究阿基米德原理，演示浮力产生原因。重构后的教学逻辑如图6所示。

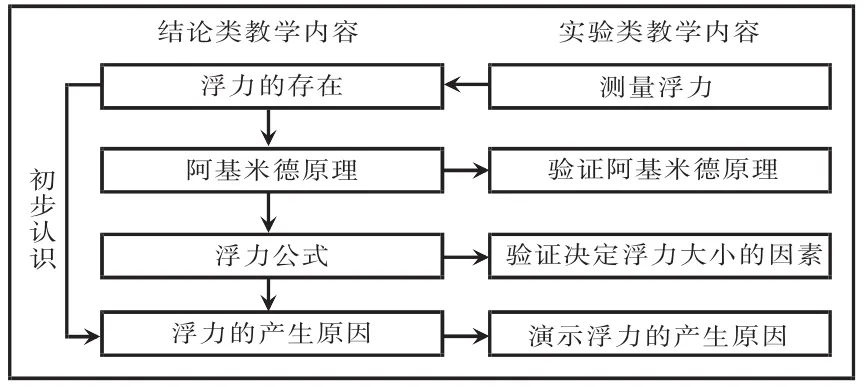
图6 “浮力”一课的教学逻辑

3.1 通过测量说明浮力存在

物体漂浮于液体表面时，学生很容易利用二力平衡的知识推理出浮力存在，而物体浸没在液体中是否受到浮力，并不直观。因而需要对浸没在液体中的物体进行测量，以给出浮力存在的证据。

如图7所示，观察到同一物体分别处于空气和液体中，弹簧测力计示数不同，学生可以意识到物体好似被托着，受到了一个向上的力，从而认识到浸没在液体中的物体也受到了浮力。

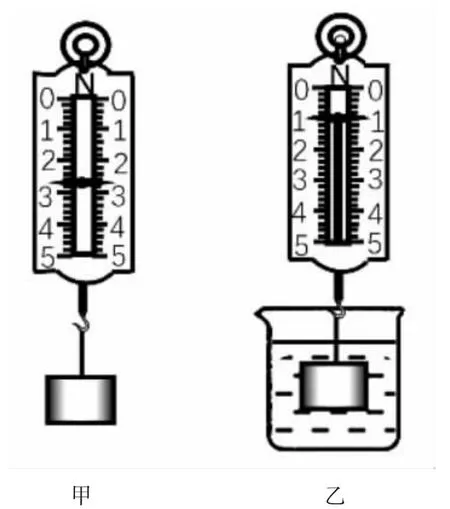
图7 测量浮力

教师再引导学生对物体进行受力分析，甲图中 F1＝G，乙图中 F2＋F浮＝G，于是 F浮＝G-F2＝F1-F2。同时，学生掌握了浮力的测量方法。

3.2 初步认识浮力的产生原因

学生已经学习过液体压强，在对图7乙中的物体进行受力分析时，可能会认为物体还受到了液体施加的压力。这时，可采用类比的方法，让学生初步认识到浮力和液体压力的关系。教师用手指按压教室的门，提问“老师对门施加的是推力还是压力”，学生已经学习过“推力和压力都属于弹力”，所以会意识到推力和压力二者并无本质区别，教师即可指出液体对物体施加的浮力和压力也无本质区别。

再以截取的饮料瓶作为实验教具，将一乒乓球置于其中，如图8所示[5]。向教具中加水，发现乒乓球不浮起，这是因为乒乓球下方并无液体，没有受到液体向上的压力；将装置放入水槽中，使得乒乓球下方与水接触，可观察到乒乓球上浮，证明浮力就是液体施加的压力。当学生初步认识到浮力和压力并无本质区别时，教师即可指出对物体进行受力分析时，若考虑了浮力，便不需要再考虑液体的压力。

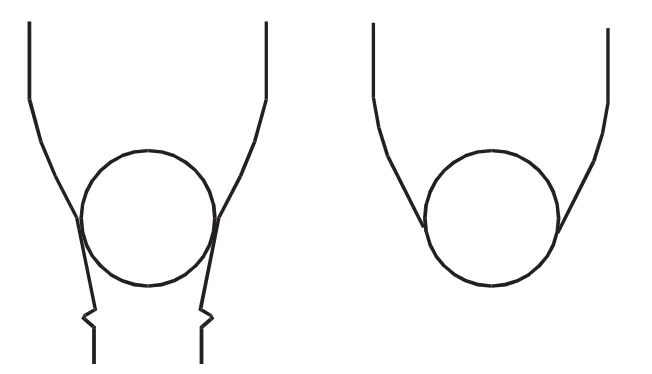
图8 截取饮料瓶

3.3 验证阿基米德原理

当学生确认浮力存在后，再利用上文所述的等效思想推理得出阿基米德原理，然后通过实验予以验证。物理学是一门实验科学，推理得出的结果必须通过实验验证。另外，直观的实验现象也是学生得以认同科学理论的重要依据，甚至对于部分学困生来说，抽象的推理过程是难以接受的，但直观的实验证据足以使其认识到阿基米德原理的内容。

3.4 验证决定浮力大小的因素

传统教学中，探究影响浮力大小因素的实验一般安排在阿基米德原理之前[6]。本文因推理得出阿基米德原理的方法不同，故可以利用阿基米德原理推导出浮力公式，从而体现出浮力公式是阿基米德原理的推论：F浮＝G排液＝ m排液g＝ρ液gV排。于是，在教学顺序上作出了调整。对于问题“影响浮力大小的因素有哪些”，学生可以根据推导出的公式进行更加合理的猜想，并能够对实验结果作出预设，“物体排开液体的体积”这个物理量也可以被理解。于是，自然地引出了两个验证性实验：验证物体所受浮力与液体密度有关；验证物体所受浮力与物体排开液体的体积有关。

3.5 再次认识浮力的产生原因

得出浮力公式后，选取图2中的长方体模型，对公式进行推导，可得

F浮＝ρ液gV排＝ρ液g（h1-h2）S＝F向上-F向下

从而使学生认识到长方体所受浮力是其下表面所受压力与上表面所受压力之差，并利用图9所示教具进行演示实验以强化认识。此时，由于初中学生数学水平的限制，研究对象才被限制在特定的模型之中。但教师仍然可以利用图10的模型，指出其他不规则形状的物体也会受到液体各个方向的压力，向上压力的合力大于向下压力的合力，因而浮力的本质是液体对物体的压力的合力，其产生原因是物体所受向上和向下的压力存在差值。同时，图10的模型也能够教给学生一种处理不规则形状物体问题的方法，对学生解决其他问题也会有所帮助。

图9 演示浮力产生原因

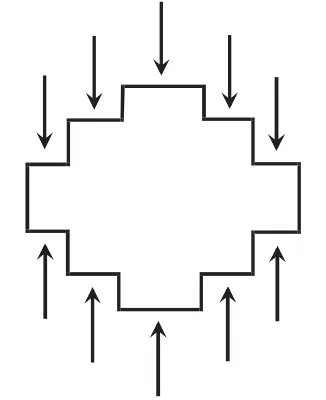
图10 不规则物体所受液体的压力

4 结语

本文利用严谨的科学推理，对“浮力”一课的教学逻辑进行了重构，重构后的公式推导过程与传统教学相反。在数学推导中，等号左右的内容是等价的，并无先后之分，所以教学逻辑不同，最终呈现出的结论却是完全一致的。但在物理教学中仍需注意，科学推理绝非纯粹的数学推导，科学工作者或是学生认识世界的逻辑是存在先后的，教师只有考虑到学生的认知发展过程，才能提升学生的科学思维素养。