基于改进麻雀搜索算法的B 样条曲线拟合方法

芦穗豪，韩勇，2，齐永阳，宋国贤

（1.中国海洋大学 信息科学与工程学部，山东青岛 266100；2.青岛海洋科学与技术国家试点实验室区域海洋动力学与数值模拟功能实验室，山东 青岛 266000）

0 概述

数字孪生是现实世界的数字化表现，是未来制造业发展转型，实现智能制造、提高工业产能的重要技术［1］。信息物理融合作为数字孪生技术的基石，贯穿于数字孪生产品的各个阶段，而如何构建数字孪生虚拟模型是实现信息物理融合的重要一环［2］。由于数字孪生虚拟模型具有高精度、高实时的特点，因此提升传统建模方法的精度与效率，是当前构建数字孪生虚拟模型亟待解决的问题。以航空发动机叶片为例，航空发动机叶片的虚拟模型与叶片截面轮廓曲线息息相关，即构建数字孪生航空发动机叶片虚拟模型，要求叶片截面轮廓曲线建模方法精确高效。

B 样条曲线造型灵活，具有许多优良特性［3］，被广泛应用于数据拟合或工业产品轮廓型线的表示中。B 样条曲线对平面点云数据的拟合是一个多维多元非线性的优化问题，许多学者对此展开了广泛研究。其中，启发式算法［4］是主要的研究方向，包括遗传算法（Genetic Algorithm，GA）［5］、粒子群优化（Particle Swarm Optimization，PSO）［6］算法和其他新型优化算法。在GA 上，YOSHIMOTO 等［7］较早利用GA 对B 样条节点向量进行编码优化；其后周明华等［8］改进节点向量编码方法，提高了初始节点向量的多样性；孙越泓等［9］将节点向量初始化与数据点分布情况相结合，提高了节点向量的优化效率；BUREICK 等［10］提出了精英策略改进GA，提升了收敛速度和拟合精度。基于GA 的节点向量优化方法流程简单，优化辅助参数较少，但普遍具有收敛速度较慢、优化效率较低的缺点。在PSO 算法上，GALVEZ 等［11］和MOHANTY 等［12］利用PSO 算法优化节点向量，但拟合精度不高；胡良臣等［13］利用PSO算法拟合带法向约束的B 样条曲线，但优化效率较差。其他优化算法在该问题上也有应用，徐善健等［14］利用混沌蚂蚁群优化算法平衡了拟合精度与搜索时间；GALVEZ 等［15］利用萤火虫算法取得了较高的拟合精度，但对不连续带有突变尖点的数据适应力较差，随后又提出采用精英克隆选择算法［16］，处理了不连续和尖点数据点的拟合，但优化效率较差；CHEN 等［17］则改进了精英克隆选择算法，但效果不大；UYAR 等［18］采用侵入性杂草优化算法，收敛速度较快，但拟合精度不高；GALVEZ 等［19］改进布谷鸟搜索算法，将其应用于B 样条边界拟合，但收敛速度过慢；UEDA 等［20］改进模拟退火算法，但搜索时间较长。不同的优化算法总存在着拟合精度与优化效率不平衡的问题，难以很好地适应用于高精度和高实时性的工程加工领域。

针对以上问题，本文提出一种结合麻雀搜索算法（SSA）的B 样条曲线拟合方法。通过随机初始化内节点向量，利用最小二乘法确定最优控制点，建立相应的适应度函数，再根据改进SSA 多次迭代计算得到自适应的内节点向量，最终确定拟合的B 样条曲线。此外，为计算符合目标精度的最少控制点数，采用二分搜索的方法改变每次迭代的控制点数量，提升传统搜索方式的搜索效率。本文以航空发动机叶片建模为实验背景，在叶片前后缘及曲线连接处连续性等研究［21］的基础上，利用基于改进SSA 的B样条曲线拟合方法对数据进行建模。

1 问题定义

本文拟解决的问题为利用B 样条曲线拟合方法对航空发动机叶片的吸力面和压力面进行高精度的曲线表达。叶片曲线表达的关键包括精度和描述复杂度，因此本文解决的问题可细化为：在给定逼进误差σ的条件下，利用最少的控制点优化B 样条曲线的拟合逼近。

B 样条曲线可表示为：

其中：t为数据点的参数化值；Sn(t)为B 样条曲线在t处的拟合点向量，控制点总数为(n+1)；B 样条曲线控制点向量集为P={P0,P1,…,Pn}；p为曲线的次数；Nj,p(t)为B 样条基函数。

Nj,p(t)定义如式（2）所示：

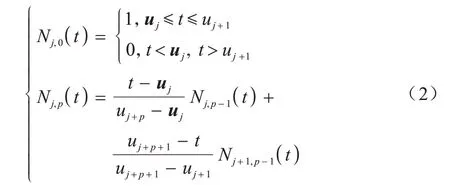
其中：Nj,p(t)的下标j、p分别为基函数的序号和B 样条曲线的次数，t为数据点的参数化值；uj为节点向量集U={u0,u1,…,um}中节点向量，uj的取值区间为［0，1］，且U满足非递减序列的特性。

通过式（2）可将B 样条曲线拟合逼近的过程分为数据点参数化、节点配置和求未知控制点3 个步骤。

1.1 数据点参数化

数据点参数化就是将一组二维坐标点参数化为数值，以便进行曲线拟合逼近，本文采用LEE［22］提出的向心参数化方法对数据点进行参数化，参数化方法可表示为：

其中：i为当前数据点的序号；(M+1)为数据点的总数；ti为第i个二维坐标点的参数化值；Dk,k-1为第k个数据点和第(k-1)个数据点的欧氏距离；Dj,j-1同理；默认t0=0。

1.2 节点配置

节点配置是指构建节点向量集U={u0,u1,…,um}的过程，即确定节点向量的数量和位置。

在参数化B 样条曲线中，曲线控制点数量、曲线次数和节点向量数量间存在式（4）的约束关系：

其中：曲线节点向量数为(m+1)；曲线次数为p；曲线控制点数为(n+1)。

节点向量集U满足非递减序列的特性，且节点向量的取值区间为［0，1］。夹 持B 样条曲线（Clamped B-Spline）［3］为通过首尾控制点的曲线，本文采用夹持B 样条曲线，节点向量还应遵循式（5）的配置：

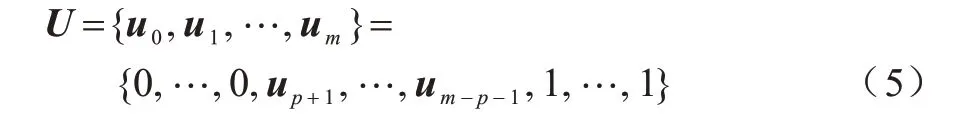
其中：U={u0,u1,…,um}表示节点向量数为(m+1)的节点向量集；up+1,…,um-p-1为一组节点向量集的内节点向量；p为B 样条曲线的次数。

1.3 未知控制点求解

B 样条曲线的拟合逼近误差为原始数据点到拟合曲线的欧几里得距离，如式（6）所示：

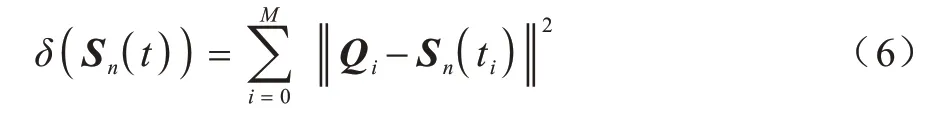
其中：δ为逼近误差；Sn(t)为B 样条曲线在t处的拟合点向量；(M+1)为原始数据点数；Qi表示第i个原始数据点向量；ti为节点的参数化值为欧几里得范数，用于计算向量长度。

由式（1）～式（5）可知，在给定一组待拟合曲线数据点的条件下，式（6）转化为以控制点和内节点向量为未知量的待解问题，如式（7）所示：

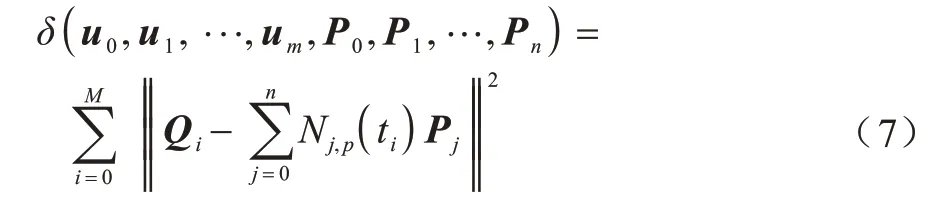
其中：δ为逼近误差；U={u0,u1,…,um}为节点向量数为(m+1)的节点向量集；P={P0,P1,…,Pn}为控制点数为(n+1)的控制点向量集；(M+1)为原始数据点数；ti为节点的参数化值；Qi表示第i个原始数据点向量；Nj,p为第j个次数为p的基函数为欧几里得范数，用于计算向量长度。

从式（7）可以看出，B 样条曲线拟合逼近问题中存在控制点与内节点向量两类未知量，该问题为一个多维多元的非线性问题。在B 样条曲线拟合逼近中，初始化内节点向量集后可用最小二乘法求得最优控制点，进而获取该内节点向量集的最优拟合曲线。因此，问题的难点就转向如何在保证精度和收敛效率情况下获取内节点向量集的最优配置。

在上述基础上，给定目标精度的最少控制点B样条曲线逼近问题可进一步表述为：求解控制点数量(n+1)，使得控制点数量在(n+1)下满足目标精度，而在n时不满足目标精度。该问题可用式（8）表示：

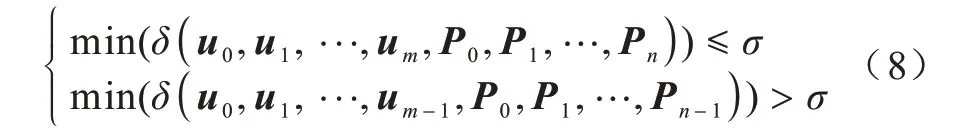
其中：σ为B 样条曲线拟合的目标精度；min 为最小值函数；U={u0,u1,…,um}为节点向量数为(m+1)的节点向量集；P={P0,P1,…,Pn}为控制点数为(n+1)的控制点向量集。

求解给定目标精度的最少控制点B 样条曲线逼近问题往往通过调整控制点数量求得。由于升序或降序的搜索方式存在效率较差、稳定性较低的缺点，因此本文利用二分搜索思想优化搜索方式，提升最少控制点求解效率与稳定性。

2 SSA

本文提出一种改进的SSA 来解决内节点向量配置的自适应优化问题。SSA 是一种从麻雀群体觅食行为中提炼出的数学优化模型［23］，较其他优化算法具有收敛速度快、稳定性好、适应性强、搜索精度高的特点。SSA 模拟了麻雀种群的捕食与反捕食行为，具体为探索者捕食、追随者跟随探索者或逃离捕食、随机生成警戒事件的3 个流程。优化问题中的每只麻雀的位置是多维的，其位置的适应度值大小则决定麻雀的探索者和追随者角色。为提高追随者的捕食率，较低能量的追随者会飞到其他区域觅食。另外，部分麻雀还负责警戒，当警戒行为发生时，它们将放弃当前食物移向新位置。

在本文问题中，麻雀表示一组内节点向量集的配置，其适应度值为该配置下的拟合误差评价值，则适应度值较小的内节点向量集作为探索者，反之为追随者。当开始迭代时，追随者会直接跃向最优解，这使SSA 在运行初期能快速收敛至某范围的适应度内，避免后续非必要的迭代。因此，SSA 更适用于高实时性的工业数字孪生场景中。在给定目标精度的工业建模中，SSA 相较于收敛较慢的PSO 和GA 有着更高的计算效率。

然而，普通的SSA 易陷入局部最优且全局搜索能力较弱。本文改进了麻雀位置更新函数和警戒行为，使SSA 能更好地应用于极值非零的优化问题，提高了迭代时的种群多样性。

2.1 探索者位置更新函数的改进

在SSA 曲线逼近问题中，探索者与追随者的位置更新直接决定内节点向量集的变化，进而影响拟合精度。在普通的SSA 算法中，由图1（a）可见，探索者非警戒更新函数随着迭代增加收敛于零，表现出局部搜索能力渐强、全局搜索能力渐弱、迭代后期易陷入局部最优的特性。此外，内节点向量分布于［0，1］，非递减序列特性在更新函数的影响下也将收敛于零，使得迭代时的种群多样性降低，同时说明原探索者位置更新方式不适用于内节点向量优化。针对上述问题，本文去除了探索者收敛为零的部分，将其修改为正态分布的随机函数，使内节点向量更新变化时上下浮动，随着迭代计算收敛于最优位置。

探索者修改后的更新函数如式（9）所示：

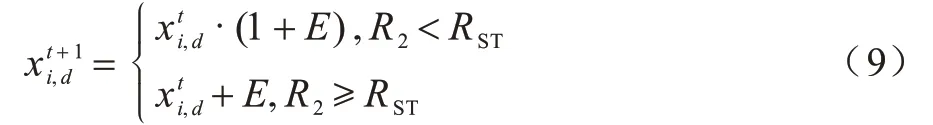
其中：E为均值为0、方差为σ2的正态分布随机数为麻雀种群第t次迭代第i只麻雀的第d维的位置；R2为警戒因子，是在［0，1］范围内的随机数；RST为警戒阈值，是［0.5，1.0］范围内的随机数；d为x的维度数。

σ2定义如式（10）所示：

其中：σ2为E的方差；b为精度因子，该值会影响位置波动范围，本文取10；(m+1)为节点向量数。

为体现更新策略的改动，图1（b）、图1（c）分别展示了探索者在非警戒和警戒下的更新策略。修改后的更新函数对内节点向量的更新有两点改善：一是在非警戒情况下，因更新函数值增添了大于1 的情况，在乘法效应下，内节点向量具备了向上跳动的特性，从而增加了内节点向量集的种群多样性；二是随着迭代次数的增加，内节点向量不再受更新函数的影响趋零变化，而是根据当前位置上下波动，这加强了算法的跳出局部最优能力，提升了全局搜索最优能力。

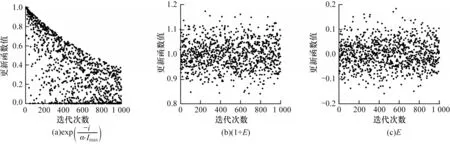
图1 探索者更新策略函数值分布变化Fig.1 Value distribution change of explorer update strategy function

2.2 警戒行为位置更新函数的改进

SSA 算法警戒行为在曲线逼近问题中表现为内节点向量的位置更新。在原始SSA 算法警戒策略中，处于最优位置的预警麻雀将向最差位置逃离，而逃离的步长因子与适应度值相关。适应度值的大幅变化造成了大步长的产生，进而影响内节点向量位置的波动距离，而较大的波动距离将导致内节点向量超出更新范围的概率变大，最终降低迭代过程中的种群多样性，同时也会造成内节点向量集构造失败；其他处于非最优位置的预警麻雀则在最优位置附近跳跃，即收敛于最优位置，这虽然加强了算法的快速收敛能力，但也易于陷入局部最优，呈现出较弱的全局搜索能力。

针对上述情况，本文对警戒行为的位置更新函数做出了修改，图2 所示为修改后的警戒策略。一方面针对处于最优位置的预警麻雀，通过将跳跃步长因子限制为［0，1］之间随机数，缩短其向最差位置跳跃的步长，步长的缩短将原本的直接跳跃策略拆分为多步靠近移动，即把当前位置与最差位置之间的情况细化并考虑在内，位置更新函数的改进提高了迭代时的种群多样性，进而提高了SSA 的全局搜索能力，使其能够寻到更优解；另一方面针对其他预警麻雀，修改为以自身位置为起点向最优位置跃进的策略，将跳跃侧重点倾向于自身位置，而非快速聚合于最优位置。这削弱了原算法中过强的快速收敛能力，让警戒行为对SSA 中麻雀的影响变得“缓和”，最终不但解决了其陷入局部最优的瓶颈，而且提高了算法的全局搜索能力。

图2 警戒策略对比Fig.2 Comparison of warning strategies

当警戒行为发生时，位置更新函数修改如式（11）所示：

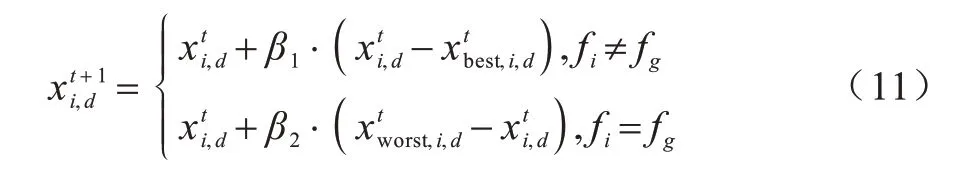
其中：t为迭代次数分别为当前迭代的麻雀种群中第i只麻雀第t次迭代的第d维位置的最差位置和最优位置；fi为第i只麻雀的适应度值；fg为最优适应度值；β1和β2为步长参数取值为［0，1］的随机数。

2.3 内节点向量更新范围

传统的SSA 算法迭代时会出现一组内节点向量中部分逆序的情况，造成B 样条曲线构造失败，导致该只麻雀“死亡”，无法参与后续优化计算，降低种群多样性。

为保证内节点向量符合B 样条曲线的构建规则，本文提出了内节点向量更新范围的概念，即为每只麻雀的单维变量建立各自的更新范围，使其在更新迭代时不会跳出该范围。

内节点向量更新范围的计算方法如式（12）所示：

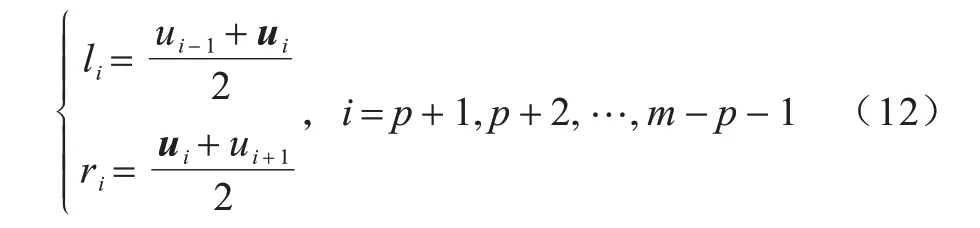
其中：i为节点向量的序号；p为B 样条曲线的次数；(m+1)为节点向量数；li和ri为第i个节点向量的左边界和右边界；ui为第i个节点向量。

图3所示为一组内节点向量更新范围的建立过程。

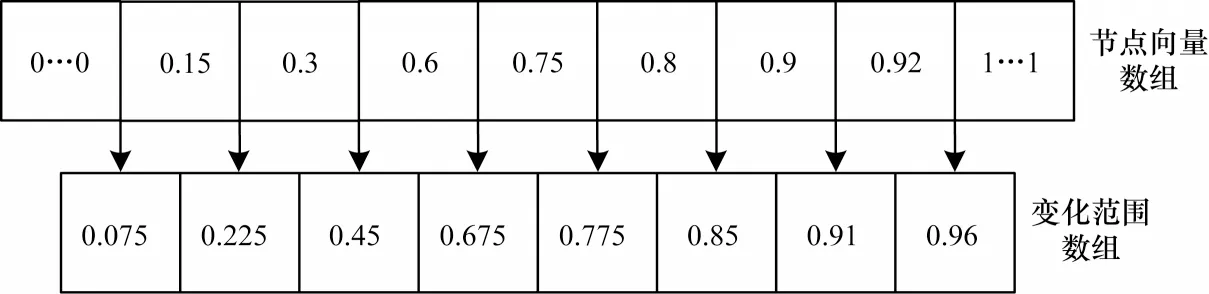
图3 内节点向量更新范围生成方法Fig.3 Generation method of internal node vector variation range

在图3 中，节点向量0.6 所对应的变化范围为［0.45，0.675］。需要说明的是，麻雀位置更新总是伴随着变化范围的更新。迭代一次内节点向量，其数值不可超出变动范围，否则将此次变动调整为内节点向量距离最近的边界值。

3 最少控制点B 样条曲线拟合的实现

改进的SSA 修改了探索者与警戒行为的位置更新函数，设定了内节点向量的更新范围，这些改进使SSA 能够跳出局部最优，具有更强的全局搜索能力，更适用于B 样条曲线拟合问题。然而，在工业数字孪生场景下，降低零件数字模型的数据量和描述复杂度至关重要。因此，问题进一步转向如何在给定曲线拟合精度的前提下，用最少的控制点实现B 样条曲线拟合。

在减少控制点问题上，传统搜索方法通过升序或逆序枚举控制点数量的方式进行求解，这种方式包含了大量冗余无效计算，具有效率过低、算法运算时间较长的缺点。本文通过实验得出控制点数量与拟合精度存在正相关关系的结论。基于此特性，本文提出了利用二分搜索的思想优化最少控制点的搜索。二分搜索方法跳过了大部分冗余无效计算，提高了整体搜索效率。

改进SSA算法中具体控制点搜索流程如图4所示。

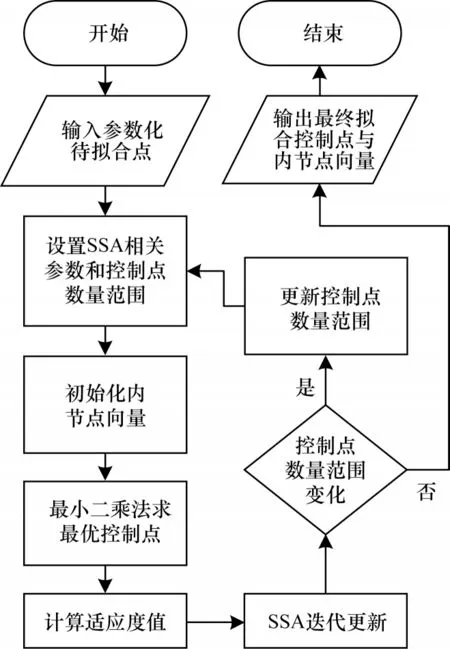
图4 改进SSA 中具体控制点搜索流程Fig.4 Search procedure of specific control points in improved SSA

SSA 相关参数的设置包括B 样条曲线次数、麻雀种群数量和迭代次数的设置。内节点向量集是根据控制点数量和一些约束条件随机生成的浮点数数组。SSA 相关参数初始化后，可通过最小二乘法计算在该组内节点向量集下的最优控制点，再计算相应的适应度值，根据适应度值进行SSA 的迭代更新。

3.1 适应度函数

适应度函数用于评价SSA 中一组节点向量集的拟合优劣程度，函数输出值是SSA 选取探索者、追随者的重要指标，影响了SSA 的优化性能。在B 样条曲线拟合问题中，适应度函数的建立考虑两个因素：一是数据点与拟合曲线的平均距离；二是数据点与拟合曲线的最大距离。平均距离可视为每个数据点具有相同的影响权重，主要在整体上影响拟合曲线与原始数据点的贴合情况，在迭代后期，受原始数据点数量和平均效应的影响，单个数据点对B 样条曲线影响程度被削减，这使得算法的局部曲线优化能力不足。而局部曲线较差的拟合效果往往伴随着较大距离误差，将数据点与拟合曲线的最大距离加入适应度计算中，提高了较远数据点的影响权重，可以改善局部曲线拟合较差的情况，进一步提升算法的B 曲线拟合效果。本文的适应度函数如式（13）所示，适应度值越小，曲线拟合效果越佳。

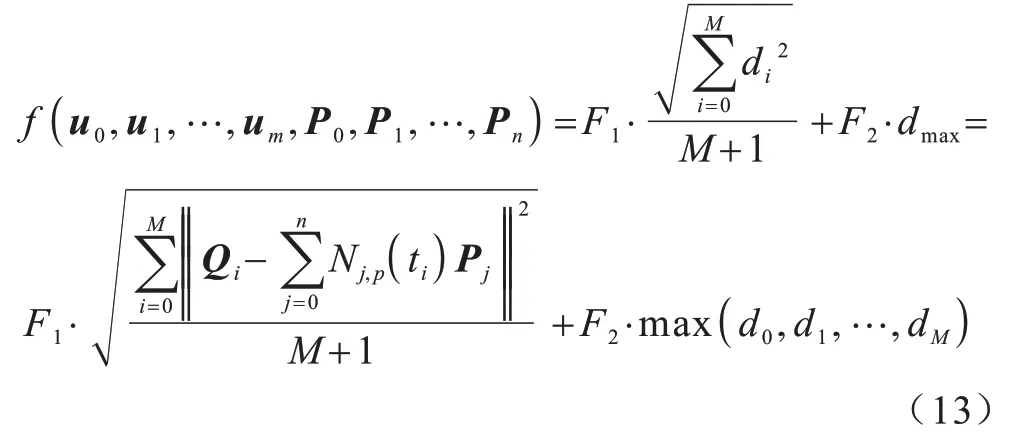
其中：f为适应度函数；U={u0,u1,…,um}为节点向量数为(m+1)的节点向量集；P={P0,P1,…,Pn}为控制点数为(n+1)的控制点向量集；(M+1)、di、dmax分别为原始数据点的个数、单个原始数据点到拟合曲线的距离和数据点到拟合曲线的最大距离；Qi为原始数据点向量；F1、F2为距离影响因子，F1、F2决定了单个数据点与所有数据点对拟合曲线的约束能力，本文中为欧几里得范数；max 为最大值函数。

3.2 最优控制点

初始化构建内节点向量后，B 样条曲线拟合逼近问题转换为一个多维单元的非线性问题，可通过最小二乘法求解最优控制点。问题转化为求曲线拟合逼近精度最小时控制点的配置，该配置为最优配置。在节点向量集已知的情况下，式（7）的曲线拟合精度可表示为：

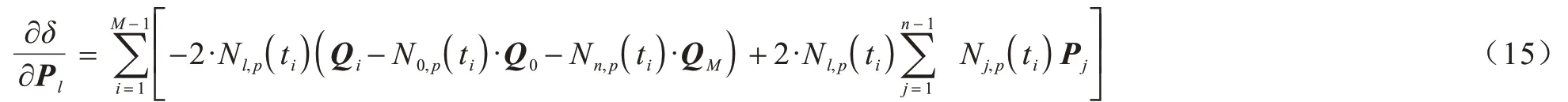
本文采用夹持B 样条曲线，头尾控制点已知，因此仅对编号1～n-1 控制点求偏导。为满足必要条件，令=0，可得：

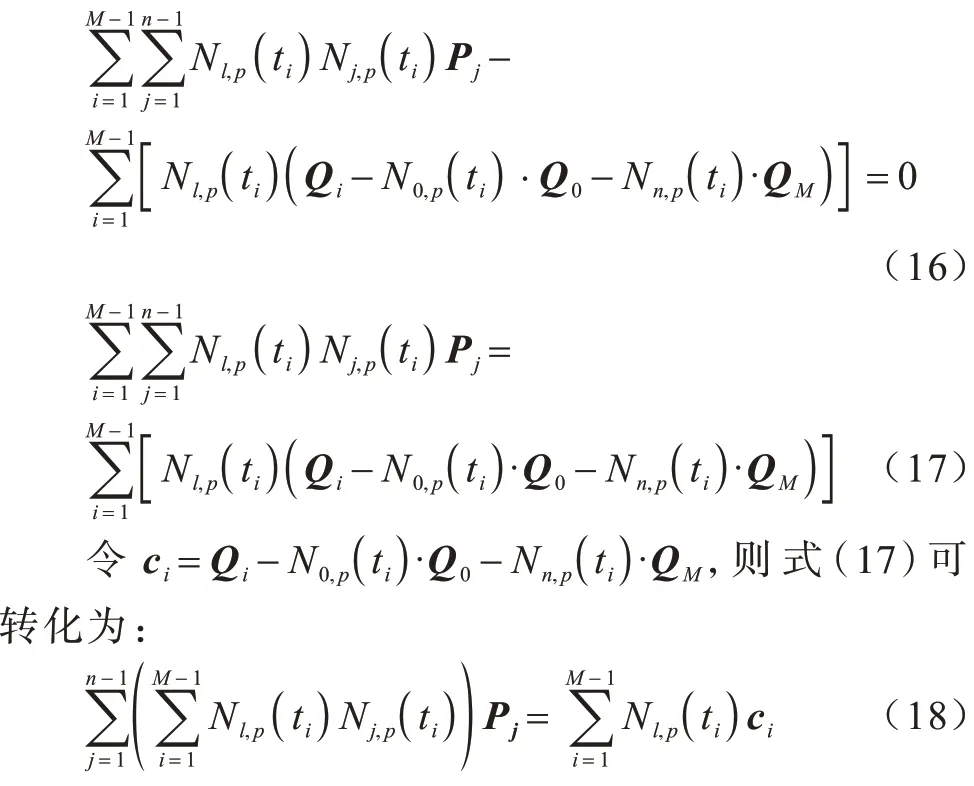
式（18）为关于控制点Pl,l={1,2,…,n-1}的n-1个线性方程式，若令l=1,2,…,n-1，可得到n-1 个方程组，其满足于：

其中：N表示大小为(M-1)×(n-1)的标量矩阵；P表示大小为(n-1) ×1 的待求控制点向量矩阵；C表示大小为(M-1)×1 的向量矩阵。

N、P、C具体表示如式（20）～式（22）所示：

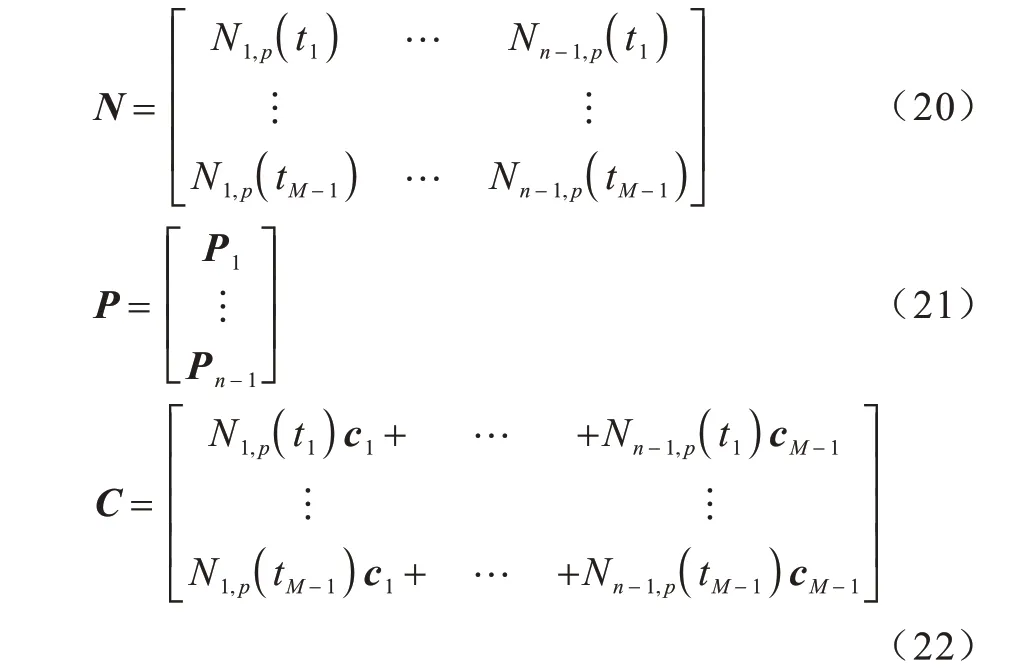
由式（19）求解最优控制点集合可通过P=(NTN)-1C，其中内节点向量在规定的更新范围内变动保证了NTN是可逆的。依据高斯消元法对n-1个方程组进行求解，可得到最优控制点集合。至此，将求得的最优控制点集合与内节点向量集合代入至式（13）中，可计算得到当前麻雀的适应度值。

3.3 最少控制点数量的二分求解

传统搜索方法通过升序或逆序枚举寻找曲线拟合的最少控制点，该方法冗余计算多，效率低，不适合实时性强的工业建模工作场景。为缩短寻找最少控制点的时间，提高运行效率，本文采用二分搜索的思想对该问题进行优化。

二分搜索的可行性是基于控制点数量与拟合精度存在正相关关系。图5 所示为使用SSA 算法在确定控制点数量的条件下取得的最优方案得到的拟合误差。可以看出，控制点数量与曲线拟合精度之间存在正相关关系。其中，控制点数量范围控制在5～16 中，实验运行500 次。

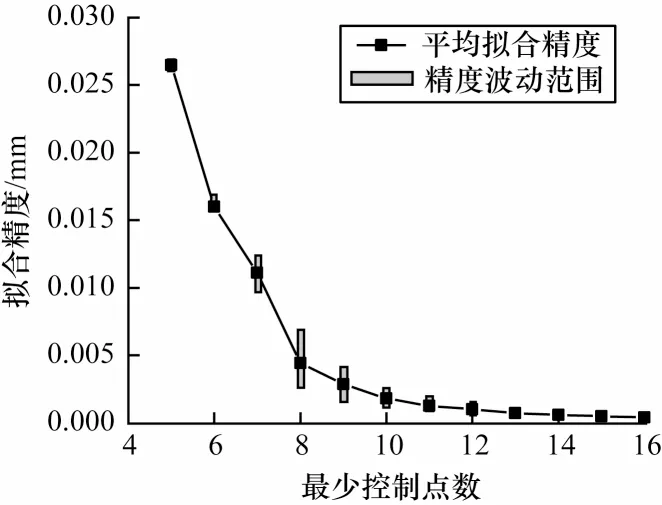
图5 最少控制点个数与拟合精度的关系Fig.5 Relationship between the minimum number of control points and fitting accuracy

受随机初始化节点向量的影响，在大量控制点情况下会导致最终的拟合精度变化极小，此时控制点数量与曲线拟合精度之间的正相关关系将减弱，此类情况可通过扩大初始种群数量改善。若将相同控制点数量的拟合精度取平均值，则此时控制点数量与拟合精度存在严格正相关关系。

二分搜索最少控制点数量依靠搜索区间与目标精度来完成。在最少控制点求解问题中，搜索区间是控制点数量的变动范围，SSA 迭代前取搜索区间中值为当前控制点数，当迭代结束后输出曲线的拟合精度，若未达到目标精度，则右移搜索区间左边界，反之，左移右边界。当搜索区间仅包含单值时，该值为最少控制点数。

3.4 时间复杂度分析

时间复杂度是评价算法性能的重要指标，本文通过提出算法的时间复杂度T'和原SSA 的时间复杂度T来研究算法效率的变化。

首先计算改进SSA 的时间复杂度T'，设置麻雀的种群规模为I，维度数为D。若初始化参数时间为Tinit，计算单个内节点向量左右边界所需时间为η1，初始化单个内节点向量所需时间为η2，最小二乘法计算最优控制点时间为Tcp，适应度函数的运算时间为Tf，则初始化时时间复杂度为：

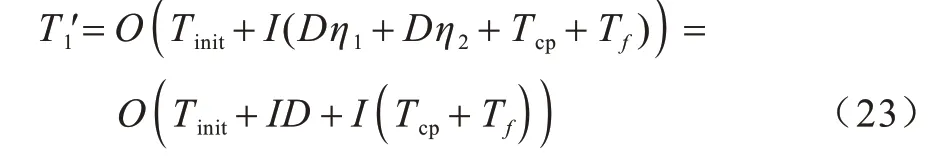
对于算法的探索者行为，由式（9）可知，修改后的探索者更新计算效率与正态分布随机数的生成效率密切相关。本文利用Box-Muller 算法［24］生成正态分布随机数，若生成正态分布随机数的时间为η3，生成R2、RST的时间为η4，更新每一维探索者位置的时间为η5，探索者占比为G1，则修改后的探索者位置更新时间复杂度为：

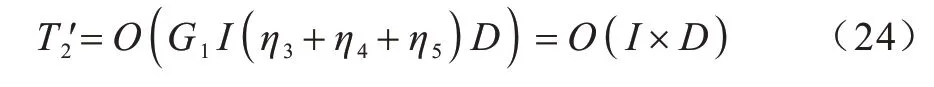
改进SSA 与原SSA 具有相同的跟随者行为，其位置更新时间复杂度为：

对于算法的警戒者行为，由式（11）可知，若两个步长因子的生成时间为η6，更新每一维的警戒者位置的时间为η7，警戒者占比为G2，则修改后的警戒者位置更新时间复杂度为：

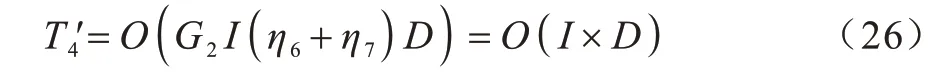
在麻雀位置更新结束后，对于内节点向量更新范围，首先需要检查一次内节点向量的位置是否越界，然后刷新内节点向量更新范围。由式（12）可知，若检查单个内节点向量越界行为的时间为η8，则内节点向量更新范围检查与刷新操作的时间复杂度为：

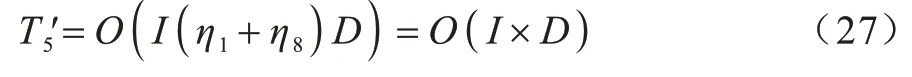
在一次改进SSA 迭代的最后，为保证下次迭代的正常进行，还需更新麻雀的适应度值并提取最优、最差麻雀，而适应度值计算的前提需要利用最小二乘法计算最优控制点。若选取最优与最差麻雀的时间为η9，则更新麻雀适应度值的时间复杂度为：

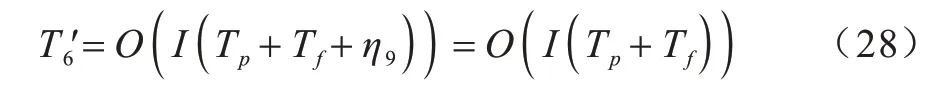
由式（23）～式（28）可知，当最大迭代次数为K与种群规模I固定时，改进SSA 算法在本文问题上应用所需的时间复杂度为：

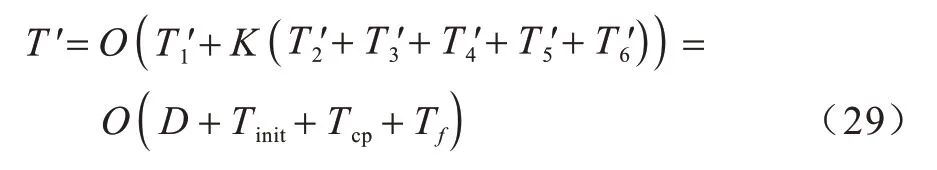
应用原SSA 与本文问题需要添加最小二乘法计算最优控制点，由式（25）可知，原SSA 的时间复杂度T为：

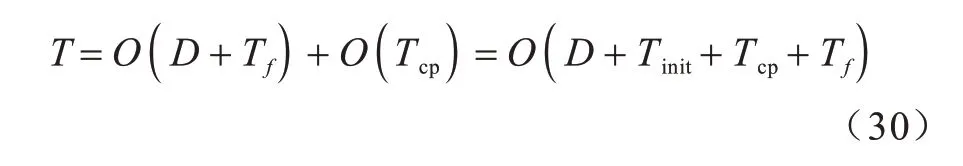
式（29）和式（30）说明了原SSA 与改进SSA 的时间复杂度保持一致，本文对探索者、警戒行为的改进没有降低原算法的求解效率。

在初始化和更新迭代过程中，B 样条曲线基函数因内节点向量变化将重新构造，为进一步分析改进SSA 在B 样条拟合问题上的时间复杂度，有必要分析B 样条基函数的时间复杂度。若B 样条节点向量数为(m+1)，次数为p，根据式（2）可得B 样条曲线基函数的时间复杂度：

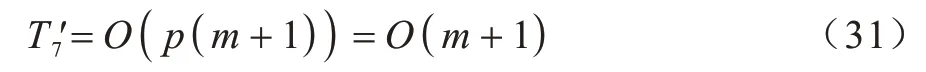
在改进SSA 参数初始化时，假设SSA 设置参数时间为η10，则初始化参数时间复杂度为：

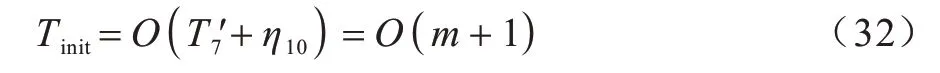
对于适应度函数，由式（13）可知，若(n+1)为控制点向量集的数量，(M+1)为原始数据点向量的数量，则在计算适应度函数时最坏情况下控制点数量为(M+1)，其适应度函数时间复杂度为：

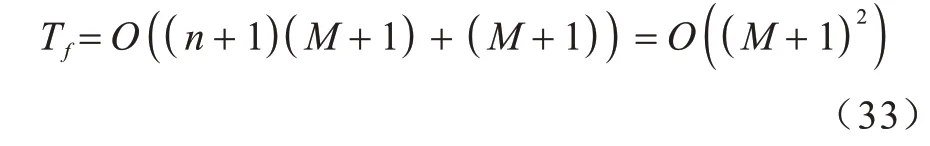
在计算最优控制点时，需要先计算内节点向量更新后的B 样条基函数，然后再根据式（19）～式（22）求得最优控制点。因此，最优控制点计算的时间复杂度为：

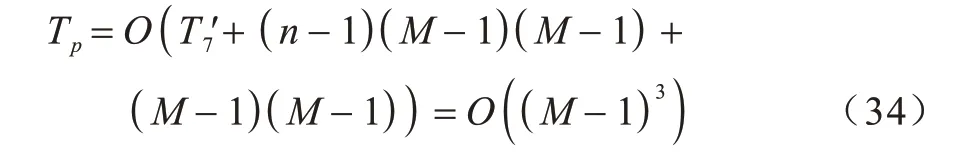
在本文问题中，麻雀维度数D即为内节点向量数(m+1-2p)，而根据式（4），内节点向量数与控制点数存在线性关系，则将式（32）、式（33）代 入式（29）后，改进SSA 在本文问题上应用的时间复杂度为：

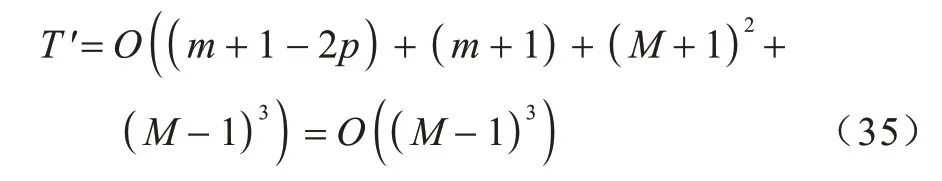
式（35）表明，改进SSA 在B 样条曲线拟合问题上的时间复杂度与原数据点输入规模相关，时间复杂度主要受限于待拟合数据点的数量。

在寻找最少控制点问题中，若寻找控制点范围为［L，R］，则二分寻找最少控制点数量的时间复杂度为：

式（36）表明，二分搜索使得最少控制点数量的搜索次数减少(R-L-lb(R-L))次，总体搜索效率有所提高。

4 实验设置与结果

图6 所示为某型航空发动机压气静转子叶片的三维模型，选取该叶片17 个截面轮廓（图6 中黑色线条）的点云数据进行压力面和吸力面的曲线逼近拟合实验，其中每个截面的点云数据是以0.001 mm 的弦公差标准取样生成，每个截面数据点为350 个左右。

图6 某型航空发动机压气静转子叶片三维模型Fig.6 Three-dimensional model of compressor stator and rotor blade of aeroengine

实验主要分为4 类：第1 类实验探究了改进SSA在B 样条曲线拟合问题上的应用可行性与正确性，实验采用17 个截面与3 组固定数量的控制点（分别为20、50、80 个）进行迭代运算；第2 类实验是为了验证二分方法寻找最少控制点的可行性与高效性，可行性探究实验在给定目标精度和初始控制点区间（搜索区间为［10，40］）的条件下，记录搜索过程中控制点数量的变化；高效性探究实验设定精度区间［0.01，0.001］、初始控制点区间［10，80］，分别统计升序、逆序、二分搜索方法的运算时间，其中精度变化步长为0.005；第3 类实验对比3 种常用的节点向量定义方法与改进SSA 的拟合精度，探求改进SSA 优化节点向量的优势；第4 类实验进一步对比3 种节点向量优化算法，评价改进SSA 的拟合效果和优化效率两方面的性能。

需说明的是，在工业建模背景下，零件建模精度为所有数据点到拟合曲线的最大距离，本文沿用该定义。

4.1 SSA 在曲线拟合问题上的应用效果

改进SSA 具有快速与高精度收敛的特性，提高了B 样条曲线拟合的精度与效率，以及叶片三维数字模型的建模精度与效率。在17 个实验截面中，针对不同的叶片截面轮廓，选取了6 个部位和轮廓曲率差异较大、具有代表性的叶片拟合结果进行展示分析。叶片截面吸力面压力面曲线拟合效果如图7所示。结果显示，拟合曲线均较好地贴合了原始数据点，这表明了改进SSA 在B 样条曲线拟合上具有较好的鲁棒性。

图7 轮廓曲线拟合效果Fig.7 Fitting effects of contour curves

图8 展示了6 组叶片截面拟合时适应度值的收敛情况，其中每组迭代固定了控制点数量。SSA 在迭代初期具有快速收敛能力，适应度值快速向最优迭代，随后趋于稳定。图8 的拟合过程验证了这一迭代规律，经过10 次左右的迭代适应度值即可趋于收敛，且曲线拟合最终都收敛，这表明了改进SSA 在B 样条曲线拟合中的可行性。

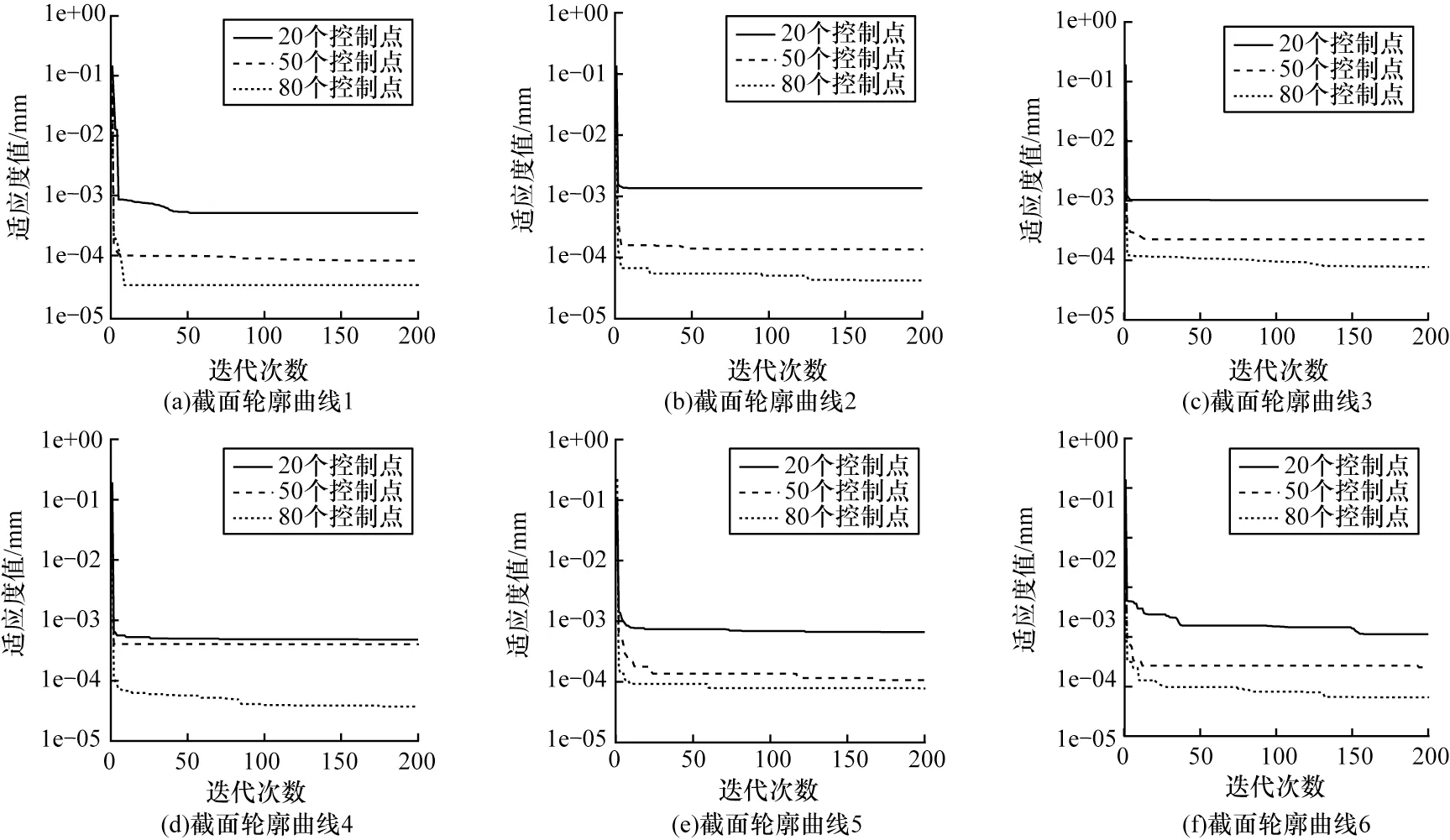
图8 截面轮廓曲线拟合迭代过程Fig.8 Iterative process of profile contour curve fitting

图8 中同一叶型曲线在拟合时，随着控制点数量的增加，迭代结束时的适应度值不断缩小，印证了控制点数量与曲线拟合精度的正相关关系。而在不同叶型、等量控制点拟合时，改进SSA 的收敛适应度值在一个数量级内浮动，这说明不同叶型会影响拟合精度。因此，工业上要使得不同叶型曲线都达到目标精度，有必要求出所有曲线达到目标精度所需的最少控制点数。

4.2 二分搜索的速度提升

二分搜索方法通过搜索区间减半的方式来提升单调性问题的搜索效率，在3.3 节与4.1 节中都验证了控制点数量与拟合精度之间的单调关系，因此本文利用二分思想求解B 样条曲线拟合所需的最少控制点，降低传统搜索方法的运算时间。图9 为截面轮廓曲线1、3、5 在目标精度为0.001 mm 时，随着二分搜索进行时不断输出的拟合精度，通过缩小搜索区间，最终控制点数固定在某值。二分搜索过程呈现出拟合精度向目标精度回归和控制点数收敛于某值的特征。由此可见，二分搜索方法在求解最少控制点问题的可行性与有效性。

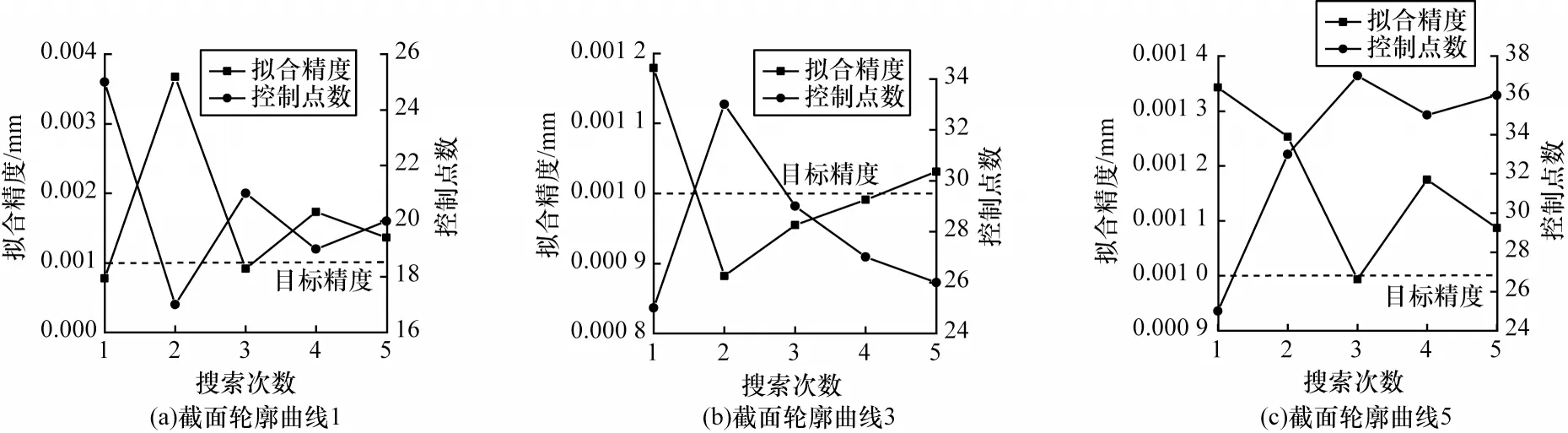
图9 二分搜索时最少控制点和拟合精度的变化Fig.9 Change of least control points and fitting accuracy in binary search

为分析二分搜索优化效率，本文对比了二分、升序、降序3 种搜索最少控制点的平均时间差异和不同精度下的搜索时间变化，实验结果如图10 所示。就平均耗时而言，二分搜索在3 条曲线上均耗时最少。以曲线3 为例，二分平均查找时比升序和降序均耗时缩短了34.6%和46.2%，这体现了二分搜索的高效性。就不同精度而言，相比升序搜索，二分搜索大幅减少了高目标精度下的搜索时间，低目标精度下也具有相似的搜索效率；相比降序搜索，二分搜索提高了低目标精度下的搜索性能，高目标精度下的搜索效率略差。另外，目标精度在［0.003，0.005］时，二分搜索比升序搜索的耗时变化更为平缓，表明二分搜索具有较强的稳定性。降序搜索方式虽也体现出了较高搜索稳定性，但其主要受益于降序搜索的结束条件和SSA 快速收敛的特性，进而主要耗时集中在较少控制点区域，这也使得降序搜索在低目标精度下表现不佳。总体而言，二分搜索在不同目标精度上都有较优表现，具有最好的整体优化效率，在不同的目标精度情况下有较强稳定性，适用于求解B 样条曲线拟合最少控制点问题。

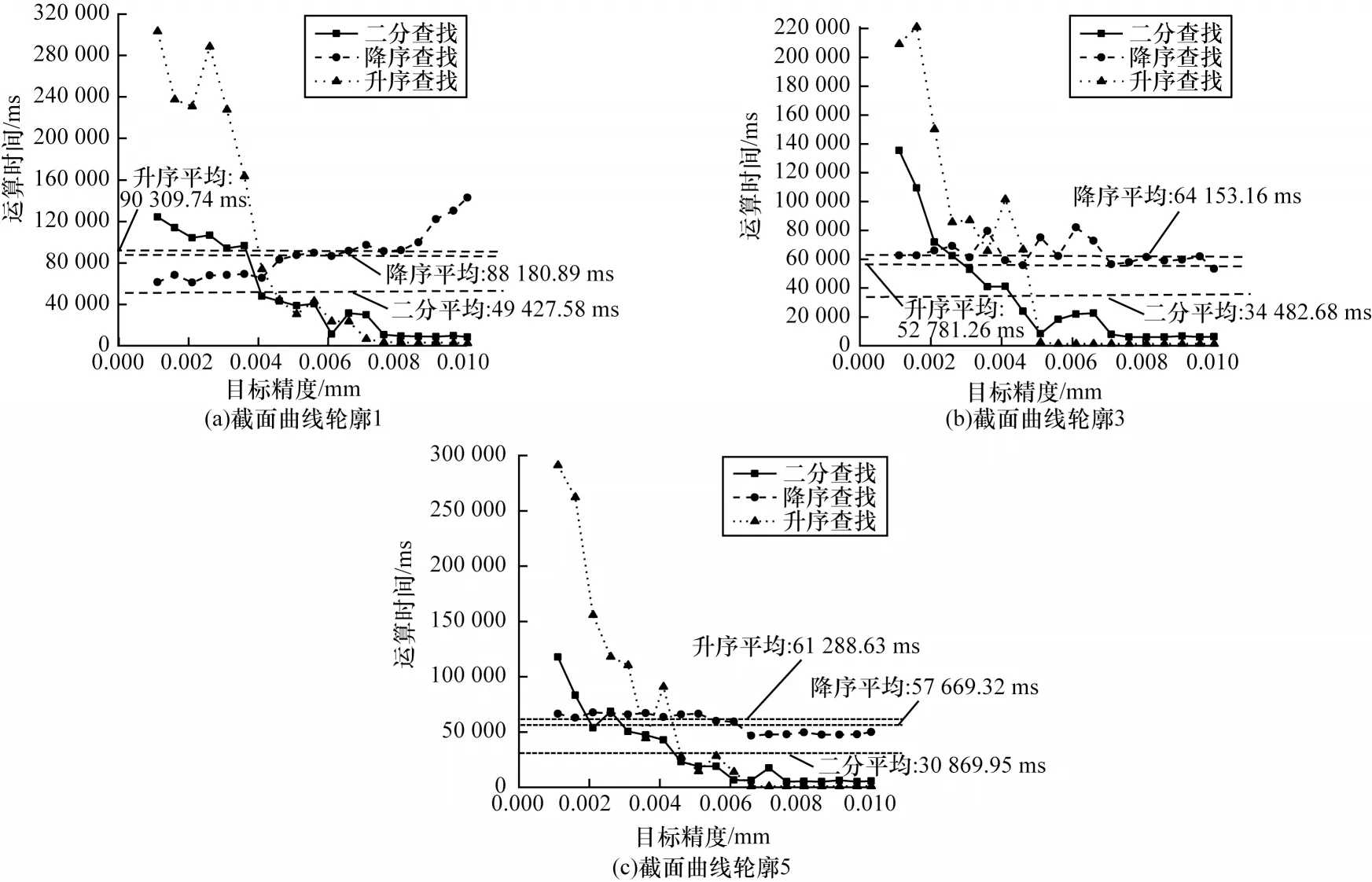
图10 不同搜索方式耗时对比Fig.10 Time consuming comparison of different search ways

4.3 改进SSA 构建自适应节点向量的优势

在B 样条曲线次数固定的情况下，选择不同的节点向量直接改变了B 样条曲线基函数的线型，进而影响B 样条曲线的最终形状。因此，B 样条曲线的拟合逼近很大程度上取决于节点向量的构建。传统的节点向量构建方法因没有考虑B 样条曲线的特殊性，很难应用于精度要求较高、曲线线型不同的场景。

为验证改进SSA 构建自适应节点向量的优势，将改进SSA 与均匀分步法［25］、平均节点法［3］、皮格尔节点法［3］3 种传统节点向量构建方法进行对比，选用最大误差（Emax）和均方误差（EMSE）进行量化分析。实验控制点数量固定为80 个，改进SSA 的迭代次数为200 次，初始种群数量为50 个。

评价指标的计算公式如式（37）所示：

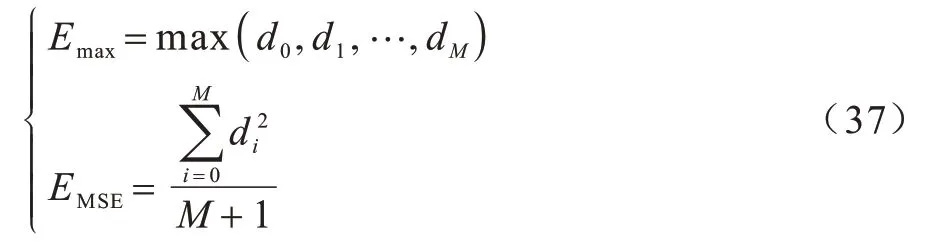
其中：Emax为最大误差；EMSE为均方误差；max 为最大值函数；di为单个原始数据点到拟合曲线的距离；(M+1)为原始点数量。

实验在17 组叶片截面轮廓曲线中进行，表1 仅记录上文展示出的6 组截面曲线的拟合结果。

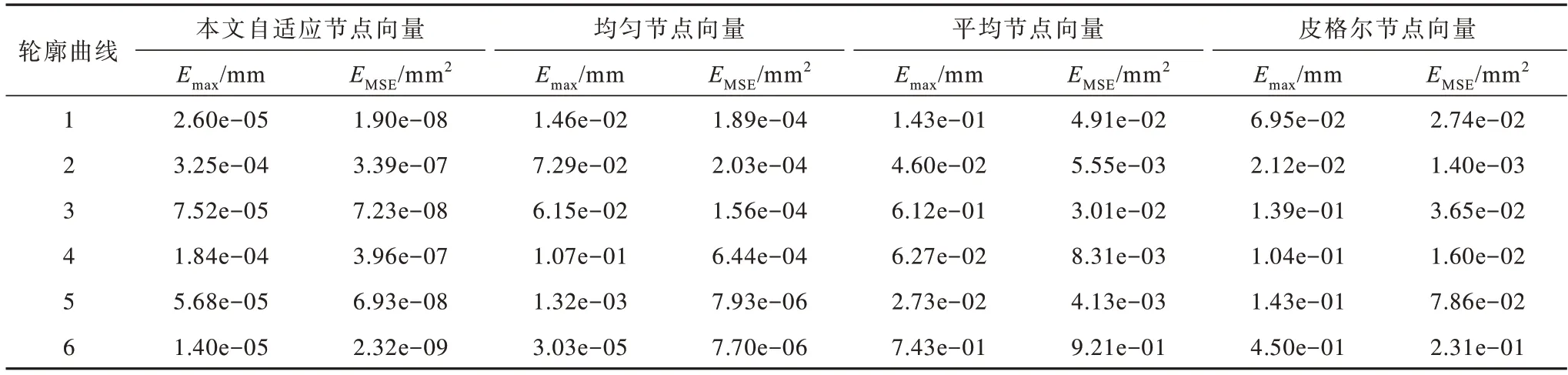
表1 不同节点向量拟合曲线对应误差Table 1 Corresponding errors of fitting curves with different node vectors

由表1 可知，本文自适应节点向量在6 组截面曲线中都取得了最好的拟合结果。以曲线3 为例，相比均匀节点向量，本文自适应节点向量的Emax降低了3 个数量级，EMSE降低了4 个数量级；相比平均节点向量，Emax降低了4 个数量级，EMSE降低了6 个数量级；与皮格尔节点向量相比，Emax降低了4 个数量级，EMSE降低了6 个数量级。在本文问题中，均匀节点向量配置相对于其他两种传统方法取得了较好的拟合效果，这可能是由于叶片吸力面与压力面曲线变化平缓，无明显突变。但均匀节点向量配置在曲线4 和曲线6 上产生了4 个数量级的误差偏差，这也说明了均匀节点向量法受拟合的曲线线型影响较大，稳定性较低。对于6 个不同的截面轮廓曲线，本文的自适应节点向量法的Emax控制在1 个数量级内，EMSE控制在2 个数量级内。由此可见，本文提出的基于改进SSA 建立的自适应节点向量在鲁棒性和精确性上均优于传统方法定义的节点向量。

4.4 与其他优化算法对比

传统节点向量构建方法存在适应性差、拟合精度较低的缺点。为提高曲线拟合精度，研究人员采用PSO［11］、GA［7］等算法生成自适应节点向量，为比较改进SSA 与其他优化算法在B 样条曲线拟合问题上的优劣程度，本文分别采用PSO、GA 和原SSA 算法对上述6 个截面点云的迭代过程进行对比分析研究。为便于分析，更好地评价节点向量的优化能力，本文控制点数量固定为20 个，迭代次数固定为200 次，设置种群数量为50 个进行实验。实验结果如图11 所示。

从迭代结束时的适应度值出发，改进SSA 拟合效果最优，PSO 与原SSA 次之，并取得了相似的拟合结果，GA 相比其他优化算法优化效果不明显。从优化效率来看，原SSA 在迭代初期适应度值快速缩小，随之陷入局部最优无法跳跃出来；改进SSA 收敛略微慢于原SSA，在50 次左右的迭代后趋于稳定，但在迭代中后期仍具有一定的跳出局部最优能力；PSO在迭代过程中不断向最优情况靠近，效率低于原SSA 和改进SSA，且对不同的截面曲线优化效果差异较大，这可能与叶型形状差异和初始化种群的随机性有关。GA 整体优化效率相比其他算法略显弱势，在迭代过程中适应度值虽呈下降趋势但降幅较小，这也导致了GA 最终无法取得较好的优化结果。

从总体上看，改进SSA 在拟合效果和优化效率上均取得了较好的结果。在200 次迭代后，改进SSA比原版SSA 有更好的拟合结果，并在迭代中后期具有一定的跳出局部最优能力。与PSO 和GA 相比，改进SSA 在拟合效果和优化效率上均有巨大优势。PSO 虽与原版SSA 有相当的拟合精度，但其劣势在于优化效率较低，无法适用于高实时性的数字孪生场景中。GA 虽对节点向量组有一定程度上的优化效果，但无论在效率上还是精度上相比其他3 种优化算法都无突出优势。

由于算法机制不同，不同算法的单位耗时也有所差异。为进一步探究上述4 种算法的优化效率，本文统计了6 个截面曲线运用上述4 种优化算法的总耗时，实验条件为80 个控制点、迭代200 次。此外，为验证数字孪生等工业应用场景下的曲线拟合效率，本文设定目标精度为0.005 mm，统计了4 种优化算法达到目标精度时的耗时情况。统计结果如表2 所示，由于GA 在迭代结束时均未达到目标精度0.005 mm，因此该部分数据为空。

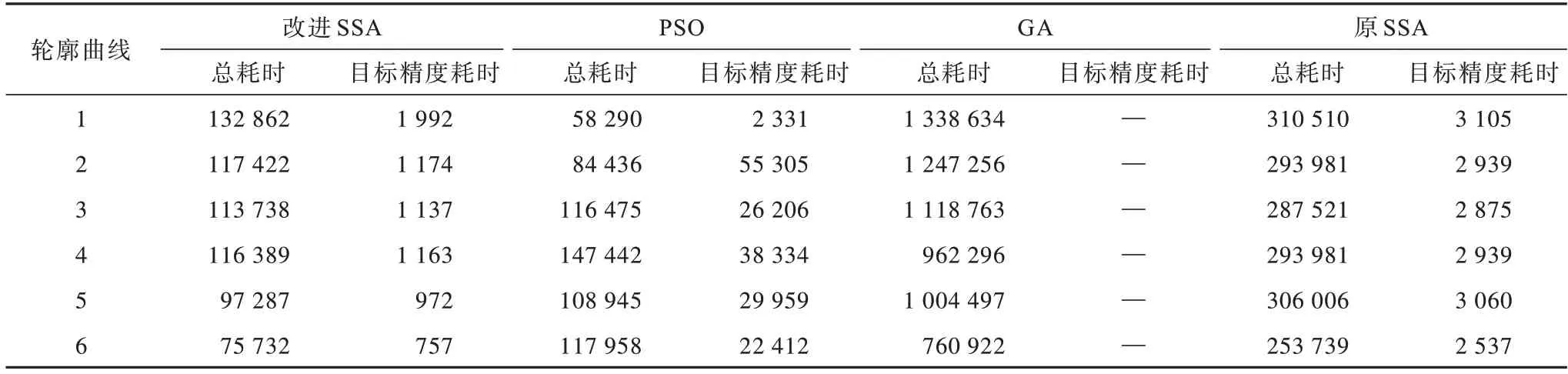
表2 不同算法下在曲线逼近上的总耗时和达到目标精度耗时对比Table 2 Comparison of total time spent on curve approximation and time spent on reaching target accuracy under different algorithms 单位：ms

在总耗时上，改进SSA与PSO显示出了明显优势。以曲线轮廓3 为例，改进SSA 的运行总耗时较PSO、GA和原SSA分别缩短了2.3%、89%和60%；改进SSA较PSO缩短了95.6%的目标精度耗时，这说明当目标精度在SSA 的快速收敛区域内时，SSA 比PSO 具有更强的收敛能力；改进SSA 较原SSA 缩短了60%的目标精度耗时，这体现了SSA 的有效改进，说明改进SSA 效率的提高源于单次迭代的运算复杂度降低。

5 结束语

本文以航空发动机叶片建模为背景，针对叶片压力面和吸力面的曲线建模问题，提出一种基于改进SSA 的B 样条曲线拟合方法。通过耦合SSA 解决内节点向量配置问题，改进SSA 的位置更新函数，以提高曲线拟合精度和算法全局搜索能力。为提高内节点向量迭代配置的鲁棒性，给出节点向量更新范围，并利用最小二乘法求解最优控制点。在此基础上，提出二分搜索方法提高算法搜索最少控制点的效率。实验结果表明，该方法能有效地建模叶片的压力面与吸力面曲线，缩短搜索最少控制点的耗时，相比传统节点向量定义法，具有更好的鲁棒性和更高的拟合精度，相比其他传统自适应算法，改进SSA在精度、效率、稳定性上都有较大的提升。本文方法保证了叶片前后缘与压力面吸力面曲线的光滑连接，达到了航空发动机叶片工业加工场景中的高精度、实时性要求。由于叶片前后缘曲率变化较快，需要大量控制点进行拟合，控制点数量的骤增会降低算法效率，因此提高多控制点数量下的算法效率是下一步研究的方向。