基于分类不确定性的伪标签目标检测算法

雷洁，饶文碧，2，杨焱超，熊盛武，2

（1.武汉理工大学 计算机与人工智能学院，武汉 430070；2.武汉理工大学 三亚科教创新园，海南 三亚 572000）

0 概述

随着深度卷积神经网络的迅猛发展，高性能并行计算的成熟以及大数据的积累，基于深度学习的目标检测技术［1-3］开始涌现并取得了突破性进展。但目前主流的基于监督学习的目标检测方法［1-2，4］的检测性能依赖于标注数据的规模，标注数据的规模越大，标注数据的类别越全面，经过学习的目标检测模型的性能就越高。在多数应用场景中，收集高精度的标注数据是十分耗费财力物力的工作，而获取大量未标注数据却较为容易。如果仅利用少量的标注数据对模型进行训练，不仅会造成严重的过拟合问题，同时也浪费了大量的未标注数据。因此，通过少量的标注数据指导，利用大量未标注数据改善检测性能的半监督学习方法逐渐得到研究人员的关注。

大多数的半监督学习方法应用于图像分类领域［5-7］和语义检测领域［8-9］，少数应用于目标检测领域［10-12］。根据模型结构以及损失函数的不同，半监督学习方法可以分为生成式方法、一致性正则化方法、基于图的方法、伪标签方法［13-15］以及综合方法［16-17］。综合方法是5类半监督学习方法中表现最为优秀的方法，其结合了伪标签、熵最小化、一致性正则化等方法并调整这些方法达到最好的表现［18］。部分研究人员将半监督学习方法与目标检测相结合来挖掘未标注数据中的信息，提高了目标检测模型的性能。

SOHN 等［10］于2020 年提出了STAC 方法，该方法将利用标注数据训练过的Teacher 模型用于预测未标注数据的检测结果，并将得到预测结果的未标注数据作为伪标签数据和标注数据用于Student 模型训练。该方法基于半监督学习的综合方法FixMatch［16］，将伪标签和一致性正则化等半监督学习方法应用到目标检测领域。但STAC 方法存在着Teacher 模型无法在线更新的问题，导致最终的目标检测模型的性能受到局限。ZHOU 等［11］于2021 年提出了Instant-Teaching 方法，该方法在STAC 方法的基础上实现了Teacher 模型在线更新，同时增加了数据增强处理操作和多Teacher 模型纠正机制提高伪标签的准确率，缓解了伪标签中错误标注给模型带来的负面影响。XU 等［19］于2021 年提出的SoftTeacher方法在Instant-Teaching 方法的基础上不仅简化了训练过程，同时对定位数据的不确定性进行评估，筛除不确定性值高的定位数据，进一步削弱了错误定位信息对模型的偏移。研究人员提出多种方法提高伪标签的准确率，减少错误标注数据用于训练，但目前基于伪标签的目标检测方法的检测性能仍然不太理想。

文献［19］认为置信度无法评估伪标签中定位数据是否准确，因此提出定位不确定性计算方法计算伪标签中定位数据的不确定性，作为筛选定位标签的主要依据。但置信度作为筛选类别标签的依据同样并不充分，因此考虑计算分类信息的不确定性作为筛选类别标签的第二依据。

深度学习中的不确定性可以分为模型不确定性和数据不确定性。模型不确定性是指模型对于自己没有学习过的数据的预测是含有很大不确定性的，可以通过增加训练数据来缓解，目前评估模型不确定性的方法主要有基于贝叶斯的方法［20-21］和基于蒙特卡洛的方法［22-23］，基于蒙特卡洛的方法由于计算量较小且不用大范围改动模型结构，因此比较受欢迎。数据不确定性是指数据中本来就存在的一种偏差或噪声，一般困难正样本比简单正样本的不确定性高，目前评估数据不确定性的方法较少，主要有基于Laplace 的方法［24］。ABDAR 等［25］通过统计9 篇论文，提出了MC-Dropout 方法，对于他们的工作极为有效。RIZVE 等［5］于2021 年提出了UPS 方法，该方法结合伪标签学习以及图像分类不确定性估计，提出一个伪标签选择框架，在CIFAR-10 和CIFAR-100数据集上表现优秀。

针对伪标签数据中错误标签难以筛除以及置信度低的正确标签较难选择的问题，本文提出一种分类不确定性计算（Classification Uncertainty Calculation，CUC）算法来计算伪标签中类别预测结果的不确定性，同时对伪标签图像的分类损失函数进行修改，以更好地反馈目标检测模型的拟合情况，在此基础上对SoftTeacher 方法中的Teacher模型在线更新公式指数滑动平均（Exponential Moving Average，EMA）进行修改，通过模型更新策略——不同权重的指数移动均值（Exponential Moving Average Different，EMAD）增强Teacher 模型和Student 模型的独立性，以进行Teacher-Student 双模型的协同训练。

1 SoftTeacher 算法及优化思路

SoftTeacher算法在伪标签目标检测领域表现较优，不仅简化了训练步骤，同时提出定位不确定性计算方法，提高了伪标签目标检测的检测性能。同时，将CUC方法、修改后的损失函数以及模型更新策略EMAD 应用于SoftTeacher 算法验证提出方法的有效性。

1.1 SoftTeacher 算法

SoftTeacher-CUC（SoftTeacher with Classification Uncertainty Calculation）算法模型结构如图1 所示。

图1 SoftTeacher-CUC 算法模型结构Fig.1 Structure of SoftTeacher-CUC algorithm model

该模型主要由伪标签生成分支和Student 模型训练分支两个分支构成。在伪标签生成分支上，未标注数据经过Weak Aug 数据增强处理后输入Teacher 模型得到预测结果，预测结果经过NMS（Non Maximum Suppression）初步选择后，其中的定位数据通过Box Jittering 方法选择得到可靠的定位数据，而分类数据通过置信度阈值选择得到可靠的预测类别。在Student 模型训练分支上，相同的未标注数据经过Strong Aug 处理和标注数据共同输入Student 模型得到预测结果，未标注数据的预测结果和Teacher 生成并被选择的预测结果一起计算损失值，标注数据按正常的目标检测训练过程计算损失值，最后用于Student 模型优化更新。Student 模型优化更新后通过EMA 方法更新Teacher 模型。

1.2 优化思路

多数伪标签目标检测方法为了避免大量标注错误的伪标签数据用于Student 模型训练，选择高置信度的伪标签数据作为训练数据。首先，由于Teacher模型没有经过预训练，因此生成的高置信度的伪标签也包含很多错误标注数据；其次，稍低置信度的伪标签数据中存在很多正确标注数据，如果能利用这些数据训练模型，可以极大地提高模型的泛化能力，缓解过拟合情况。因此，引入除置信度以外的判断依据来挖掘稍低置信度中的正确标注数据用于模型训练。受到文献［22］的启发，本文提出了CUC 的分类不确定性计算方法，用于伪标签生成分支中选择可靠的分类数据。

目标检测领域应用最广泛的分类损失函数是交叉熵损失函数，交叉熵损失函数主要是通过置信度来计算真实分布和预测分布的差异。由于增加了分类不确定性这一评估预测分布的新依据，因此考虑将分类不确定性作为权重加入到分类损失函数中，使损失函数更具代表性、更加贴合预测分布和真实分布的差异。

伪标签目标检测方法的Teacher-Student 模型结构采用了一致性正则化的思想。文献［18］针对一致性正则化方法提供了两种方法可以提高伪标签质量。第一种方法是仔细选择数据增强方法，避免引入更多噪音；第二种方法是仔细选择Teacher 模型，而不是简单地复制Student 模型。因此，Teacher 模型和Student 模型相似性高，不利于一致性正则化方法起效，本文受指数移动平均归一化（Exponential Moving Average Normalization，EMAN）方法［26］的启发，提出基于EMAD 的Teacher 模型更新方法。

2 SoftTeacher-CUC 算法

2.1 CUC 方法

在伪标签目标检测领域中，根据全连接层和softmax 函数将特征图转化为每一类的类别概率（即置信度），通过选择置信度最大的类别作为最终的预测类别，并选择最终预测结果的置信度高于置信度阈值的数据作为训练数据。

研究人员利用softmax 的置信度表示预测结果的不确定性，如果某一类别的置信度远远高于其他类别置信度就认为该预测结果的不确定性低。但文献［22］的实验表明，一些置信度高的预测结果仍然具有高不确定性。因此，受到文献［22］的工作的启发，本文提出了CUC 的分类不确定性计算方法。

2.1.1 CUC 方法思路

模型预测不确定性可以通过模型参数的分布得到，而高斯分布作为统计领域强大的工具常用于模拟模型参数的分布，因此可以通过计算模型参数的高斯分布来得到不确定性，但计算高斯分布需要庞大的计算量。GAL 等提出加入dropout 层的神经网络可以近似高斯分布的变分推理，因此模型预测不确定性计算可以简化为通过dropout 多次采样和计算方差得到。

CUC 方法的思路是：首先在Teacher 模型分类模块的全连接层前添加dropout 层，实现近似高斯分布的效果；其次通过将训练数据反复输入分类模块得到预测结果实现采样操作；最后通过计算方差实现模型预测不确定性的量化。CUC 方法的具体流程如图2 所示。

图2 CUC 方法流程Fig.2 Procedure of CUC method

首先将单张图片生成的检测框输入带有dropout 层的分类回归模块若干次，得到若干次的预测结果；其次计算若干次预测结果的方差，将预测结果的方差作为该目标分类结果的不确定性。通常认为重复预测的次数越高，计算得到的方差越具有代表性，但频繁的重复预测会延长模型的训练时间，因此本文参考UPS 方法，重复预测10 次。

通过上述方法计算得到的目标的不确定性可以代表模型对该类目标的学习程度。如果模型之前从未学习或学习了很少该类目标，则不确定性就会很高；相反如果模型之前学习过该类目标或者类似的目标，则不确定性就会较低。因此，不确定性可以在一定程度上反映模型对于输入数据的学习程度，从而判断预测结果是否可靠，帮助筛选出更可靠的伪标签数据。

2.1.2 CUC 方法实现

在SoftTeacher 方法中，Teacher 模型由特征提取模块ResNet-50、多尺度特征融合模块FPN（Feature Pyramid Network）、候选框生成模 块RPN（Region Proposal Network）和分类回归模块组成。由于分类操作主要是发生在分类回归模块，因此在分类回归模块中添加丢弃概率为0.3 的dropout 层，修改后的分类回归模块具体结构如图3 所示。

图3 分类回归模块结构Fig.3 Structure of classification regression module

CUC 方法的算法描述如下：

算法1分类不确定性计算

输入RPN 模块生成的检测框数据

输出每个检测框的不确定性

1.将Teacher 模型的dropout 层设置为train 状态。

2.将单张图片的检测框数据输入分类回归模块10 次，得到10 次的分类预测结果。

3.将得到的10 次分类预测结果拼接成尺寸为10×N×C的张量，其中，N 表示检测框的数量，C 表示类别数量。

4.计算方差得到尺寸为N×C 的方差张量。

5.选择伪标签中检测框的预测类别对应的方差作为检测框的不确定性，得到尺寸为N 的不确定性张量。

6.将Teacher 模型的dropout 层设置为val 状态

2.2 分类损失函数

SoftTeacher 方法中损失函数由标注图像的损失函数和伪标签图像的损失函数组成，具体的公式如下：

其中：Ls表示标注图像的损失函数；Lu表示伪标签图像的损失函数；α表示伪标签损失函数的权重，一般根据标注图像和伪标签图像的比例设置。

标注图像的损失函数和伪标签损失函数的具体公式如下：

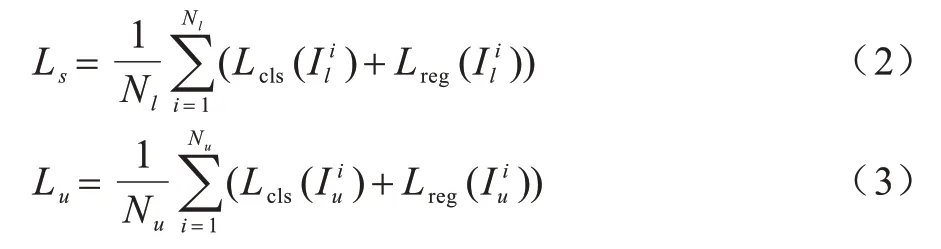
其中：Nl和Nu分别表示标注图像数量和伪标签的图像数量；Lcls和Lreg分别表示检测结果的分类损失函数和定位损失函数；和分别表示第i张标注的图像和第i张伪标签图像。SoftTeacher 方法中用到的分类损失函数和定位损失函数与Faster RCNN［1］模型相同，但对伪标签的分类损失函数进行了一定的修改，对背景检测框的损失附加权重，具体的公式如下：

其中：Gcls表示Teacher 模型生成并经过筛选的伪标签分类结果；lcls表示损失函数即交叉熵公式；rj表示第j个背景检测框的置信度，由Teacher 模型生成；和分别表示前景检测框的数量和背景检测框的数量。

通过伪标签分类损失函数式（4）和式（5）可以看出，SoftTeacher 仅采用了模型的全连接层生成的置信度计算分类损失，并反馈给模型进行模型参数更新。由于在2.1 节中实现了分类不确定性的计算方法，可以得到新的衡量模型分类质量的指标，因此修改伪标签图像分类损失函数，将分类结果的不确定性作为权重加入到损失函数中。修改后的伪标签分类损失函数的具体公式如下：

其中：uj表示第j个检测框的不确定性值。

分类困难目标和模型学习不充分目标的不确定性高，不确定性数值作为权重后导致该类目标的预测结果在整个损失值中的占比下降，该类目标对模型更新造成的影响会减弱，缓解了错误标注目标对Student 模型训练造成的负面影响。修改后的伪标签分类损失函数包含了预测结果的两个评估指标，可以反馈给模型更全面的信息，提高模型的优化程度。

2.3 Teacher 模型更新方法

在SoftTeacher 方法中，更新Teacher 模型采用的是深度半监督学习领域最常使用的EMA 方法。EMA 方法的具体公式如下：

其中：和分别表示Teacher 模型在t-1 时刻和t时刻的模型参 数；表示Student 模型在t时刻的模型参数；β表示Teacher 模型和Student 模型的占比权重，绝大多数伪标签目标检测方法将该超参数固定为0.9，而在SoftTeacher 方法中，β会随着训练的迭代次数减少。

通过上述公式可以观察到：传统的Teacher 模型更新方法表明Student 模型在式（7）中占比很低，表明Teacher 模型参数更新后的改变很小，导致整个训练过程由于Teacher 模型更新提升缓慢而漫长。SoftTeacher 在训练前期，Student 模型在更新中占比非常高，但考虑到Teacher 模型和Student 模型太过一致的问题，到训练后期Student 模型在更新中占比下降。虽然这一方法在训练中有利于检测性能的提高，但训练后期不再进行大幅更新，也限制了Teacher 模型的性能提高，从而限制Student 模型的性能提高。受到文献［26］的启发，本文提出基于EMAD 的Teacher 模型更新策略。

2.3.1 EMAD 方法思路

EMAD 方法主要是将Teacher 模型的参数根据模块作用分为特征提取模块参数、FPN 模块参数、RPN 模块参数、分类回归模块参数以及BN（Batch Normalization）层的不可学习参数5 个部分。不同部分的参数采用不同的更新方法。

由于模型的特征提取模块、多尺度特征融合模块和候选框生成模块主要是对图像特征进行处理，因此采用SoftTeacher 中的原EMA 方法对Teacher 模型中的上述3 个模块进行更新。但分类回归模块的作用是对目标的分类和定位，一旦参数和Student 模型相似会导致伪标签数据和Student 模型预测结果接近，因此减少EMA 方法中Student 模型占比，降低两个模型参数的相似，将β设置为固定的0.5。

BN 层的主要作用是对每层神经网络的输入输出值进行标准化处理，使输入输出值位于正态分布范围，以此避免梯度消失的问题。BN 层对输入值处理的具体公式如下：

其中：n表示批处理大小；μ和σ2表示该批数据的均值和方差，是BN 层的不可学习参数；γ和β表示可学习的模型参数；ε表示常量。EMA 方法对Teacher 模型的BN 层的参数进行更新，BN 层中γ和β参数来源于Student 模型，而μ和σ2参数来源于最近一批数据，两种类型的参数不一致，容易对Teacher 模型造成负面影响。因此，利用EMA 方法对不可学习参数μ和σ2进行更新，保持两种参数的一致性，具体的更新公式如下：

2.3.2 EMAD 方法实现

Teacher 模型更新算法如下：

算法2Teacher 模型更新算法

3 实验

3.1 数据集和评价指标

本文将改进后的SoftTeacher 算法在MS COCO公共数据集上进行了实验。MS COCO 包含80 种类别的目标，主要由训练集train2017、验证集val2017和无标签数据集unlabeled2017 三个数据集组成。训练集train2017 有118 000 张标注图像，验证集val2017 有5 000 张标注图像，无标签数据集unlabeled2017 有123 000 张未标注的图像。

SoftTeacher-CUC 算法的训练数据和SoftTeacher保持一致。首先在train2017 中分别随机抽取占train2017 总数量1%、5%和10%的图像分别构成多个标注数据集，剩下的图像作为未标注数据集。模型在新构成的标注数据集和未标注数据集上进行训练，在验证集val2017 上进行性能评估。

实验所用到的评估指标是目标检测领用通用的平均精度均值（mean Average Precision，mAP）评估指标，mAP 越接近于1，则检测精度越高。单个类别AP 指的是PR（Precision-Recall）曲线与X轴围成的图形面积。

3.2 模型参数设置

SoftTeacher-CUC 算法的模型结构中Teacher 模型和Student 模型采用与SoftTeacher 实验一致的Faster RCNN 模型，并结合了FPN 模块。特征提取模块采用在ImageNet 预训练的ResNet-50 模型参数初始化，其他模块的参数采用随机初始化的方法。

SoftTeacher-CUC 算法模型在单个GPU 上训练，批处理大小是5（真实标注图像是1 张，未标注图像是4 张），使用随机梯度下降（Stochastic Gradient Descent，SGD）调整学习率，初始学习率是0.001，权重衰减为0.000 1，训练180K～720K 个epoch。

定位不确定性计算方法的超参数保持不变，重复定位10 次，选择不确定性低于0.02 的检测框为伪标签中的定位数据，检测框的偏移处理是在4 个定位信息中随机选取一个进行偏移量在[-6%,6%]中的偏移操作。CUC 分类不确定性计算方法中dropout 层的丢弃率为0.3，重复分类10 次，选择伪标签中分类数据的不确定性低于0.05 但置信度高于0.7 的伪标签用于Student 模型训练。

3.3 实验结果与分析

3.3.1 不同置信度阈值对比实验

本文通过CUC 方法计算伪标签数据中分类数据的不确定性作为选择可靠伪标签数据的第二依据，但需要通过实验选择合适的不确定性阈值和置信度阈值用于伪标签筛选。

参考UPS 方法和SoftTeacher 方法，不确定性阈值和置信度阈值分别初始化为0.05 和0.9。由于减小不确定性阈值导致大量错误标注数据用于训练，造成模型在训练中平均精度均值较低，因此该对比实验主要是研究在不确定性阈值保持0.05 不变的情况下不同置信度阈值的模型训练情况。分别在标注数据占训练数据的1%、5%和10%这3 种情况下进行实验，实验结果如图4 所示。

图4 不同置信度阈值对比结果Fig.4 Contrast result of different confidence thresholds

从图4 的实验结果可以看出，当置信度阈值保持 和SoftTeacher 相同的0.9 时，Student 模型的检测性能比SoftTeacher 方法中模型的检测性能要稍低。但随着置信度阈值下降，越来越多的低不确定性伪标签数据用于Student 模型训练，Student 模型的检测性能也越来越高。当置信度阈值降低到0.7 时，Student 模型的检测性能逐渐保持稳定。因此，最终选择置信度阈值为0.7。

3.3.2 消融实验

为了验证SoftTeacher-CUC 算法的有效性，SoftTeacher算法（包 括SoftTeacher-CUC 算法和Baseline 算法）都在单GPU 环境下训练，训练迭代次数、批处理大小以及学习率都保持一致。但Baseline算法在单GPU 下训练的性能和本文有一定差距。为了比较的公平性，运用单GPU 下训练的性能与SoftTeacher-CUC 算法进行比较。实验结果如表1所示。

表1 消融实验数据对比Table 1 Comparison of ablation experiment data %

从表1 中Baseline 和Baselin+CUC 的对比实验可以看出，结合CUC 分类不确定性方法的模型性能比原模型性能分别提高了1.2、0.9和1.3个百分点，说明CUC方法在提高模型的检测性能方面是有效的。随着标注数据从1%增加到10%，模型的检测精度提高程度也从1.2 增加到1.3 个百分点，说明标注数据越多，CUC 方法越有效。下一步研究将增加未标注数据量比较的实验，观察未标注数据量的增加是否会对结合CUC 方法的伪标签目标检测算法有影响。

从表1 中Baselin+CUC 和Baseline+CUC+EMAD的对比实验可以看出，结合EMAD 方法的模型比没有结合EMAD 方法的模型的检测性能分别提高了0.2、0.3 和0.4 个百分点，说明Teacher 模型更新方法EMAD 对模型检测性能的提高起到积极作用。

3.3.3 可视化实验

为了更好地观察SoftTeacher-CUC 算法在检测性能上的提升，本文通过免费图像网站选择一张图像，测试经过相同训练的SoftTeacher-CUC 算法和SoftTeacher 算法的检测性能，图像检测结果如图5所示。

图5 SoftTeacher-CUC 和SoftTeacher 算法检测效果对比Fig.5 Comparison of detection effects of SoftTeacher-CUC and SoftTeacher algorithms

从图5（a）和图5（b）可以看出，在标注数据为5%时，SoftTeacher-CUC 算法的检测效果要优于SoftTeacher 算法的检测效果；从图5（c）和图5（d）可以看出，在标注数据为10%时，SoftTeacher-CUC 算法的检测效果要略优于SoftTeacher 算法的检测效果。上述实验结果表明：本文提出的改进算法在标注数据较少时优势明显，检测性能的提升效果更好。

3.3.4 横向实验

本文选择了伪标签目标检测领域中前沿的4 种算法与SoftTeacher-CUC 算法进行横向对比，分别是STAC算法［10］、Unbiased Teacher算法［12］、Instance-Teaching 算法［11］和SoftTeacher 算法［19］。由于一些伪标签目标检测算法的训练环境要求较高，仅引用了其实验结果，一些满足训练环境需求的伪标签目标检测算法将在与SoftTeacher-CUC 算法相同的训练环境下训练。具体的对比数据如表2 所示。

表2 横向实验数据对比Table 2 Comparison of transverse experimental data %

从表2 中可以看出，本文算法的检测精度优于其他4 种伪标签目标检测算法。同时，也证明了本文提出的改进算法对于伪标签目标检测算法能够起到优化、提高性能的作用。计划在下一步的研究中将本文提出的算法应用于其他的伪标签目标检测方法中，以证明本文算法的通用性。

4 结束语

针对伪标签目标检测算法中低置信度的伪标签数据无法被利用，导致模型过拟合、检测性能不理想的问题，本文提出一种基于分类不确定性的伪标签目标检测算法来确定伪标签数据的分类不确定性，从而筛选出更高质量的伪标签用于Student 模型训练，通过对伪标签数据的分类损失函数进行修改，将不确定性加入损失函数中，并修改了Teacher 模型的更新策略，在此基础上对Teacher 模型的不同模块调整Student 模型参数在更新中的权重。实验结果表明，改进算法有效地改善了伪标签目标检测中存在的问题，提高了模型的检测性能。下一步将在本文研究的基础上对Teacher 模型更新算法进行修改，使Teacher 模型更新和Student 模型更新相互独立，并不直接相关，使一致性正则化的算法具有更大的作用，从而提高模型的检测性能。