进化迁移优化算法综述

伍洲，杨寒石，邬俊俊，张海军，宋晴

（1.重庆大学 自动化学院，重庆 400044；2.哈尔滨工业大学（深圳）计算机科学与技术学院，广东 深圳 518055；3.北京邮电大学 人工智能学院，北京 100876）

0 概述

目前，智能优化已经成为科学和工程领域的研究热点之一，可为复杂优化问题寻找最优解决方案［1］。常用优化算法可分为确定性算法和启发式算法。确定性算法例如线性规划［2］、非线性规划［3］和最小二乘法［4］等，利用问题解析性质求解目标函数的全局或近似全局最优解［5］。启发式算法例如遗传算法（Genetic Algorithm，GA）［6］、差分进化（Differential Evolution，DE）算法［7］和蚁群算法［8］等，基于随机过程搜索目标函数的全局或近似全局最优解。虽然确定性算法在线性或二次规划问题中可保证最优解，但启发式算法更加灵活且易于实现，特别是对于“黑盒”优化［9］、非凸优化［10］、NP 难组合优化［11-12］和大规模优化［13-14］等问题有较强的搜索能力。进化算法（Evolutionary Algorithm，EA）是模拟自然界生物进化的启发式算法［15-17］，已成功应用于解决生物信息学、网络安全等领域的优化问题［18-19］。传统EA 在解决某个问题时往往默认先验知识为零，从零开始进行随机搜索［20-21］。然而，现实问题很少孤立存在，从已解决或正在解决的相关问题中提取的有效信息可以引导EA 高效解决新问题，降低计算过程的时间成本，提升计算结果的质量［22］。近年来，在机器学习中利用已解决任务的有用信息可求解相似学习任务，这种思想被称为迁移学习（Transfer Learning，TL）［23］。然而，现有关于TL 的研究多数局限于机器学习和深度学习的应用，例如基于TL 的机器视觉［24］、医学图像识别［25］和机器故障诊断［26］等，将TL与EA 相结合的研究较少。通过学习历史任务或正在优化任务中的有效知识，并迁移解决相关优化问题的进化算法统称为进化迁移优化（Evolutionary Transfer Optimization，ETO）算法［27］。

现有少量国外研究成果与本文研究方向类似。文献［23］首先简要概述了2016 年至2021 年多任务进化计算领域的研究；其次重点介绍了多任务进化计算的基本实现方法，例如染色体编码和解码方案、何时进行知识迁移及个体评估和选择方法等；然后介绍了多任务进化计算的相关扩展问题，例如算法框架、任务相似性度量和超多任务优化问题等。文献［27］对ETO 领域已有工作进行了分类和概述，根据ETO 算法解决问题的类型将现有ETO 研究归纳为用于不确定环境优化的ETO 算法、用于多任务优化的ETO 算法、用于复杂优化的ETO 算法、用于多目标优化的ETO 算法及ETO 算法在机器学习上的应用等5 个方面。文献［28］首先重点介绍了进化多任务优化（Evolutionary Multitask Optimization，EMTO）中任务选择方法和任务迁移方法及两者的关系；然后讨论了EMTO 与EA 的融合问题，例如EMTO 算法在复杂优化问题上的应用、EMTO 算法演化过程中的资源分配策略和进化算法搜索策略等。文献［29］根据知识迁移的模式（显式或隐式）、算法的动态性质（静态或自适应）及算法的设计模板（多因子优化或多种群多任务优化）对已有EMTO 算法进行分类和综述。本文介绍ETO 的基本分类，并从源任务选择、知识迁移、缩小搜索空间差异、进化算法搜索、进化资源分配等5 个角度入手对已有ETO 研究进行分类和综述。

1 进化迁移优化分类

进化迁移优化是一种将迁移优化（Transfer Optimization，TO）的概念与进化算法结合在一起，将历史任务或正在优化任务的种群演化轨迹、个体信息等知识迁移到相关新问题的EA 中，从而提升EA 优化性能的范式。目前，迁移优化可分为顺序迁移优化（Sequential Transfer Optimization，STO）［30］、多任务优化（Multitask Optimization，MTO）［31］和多形式优化（Multiform Optimization，MFO）［32］。STO 旨在解决顺序发生的任务，将解决历史任务获得的知识迁移到新任务中。MTO 旨在解决同时发生的多个任务，将任务优化过程中获得的知识共享给其他任务。MFO 旨在通过使用不同的替代公式解决单个任务。

1.1 顺序迁移优化

顺序迁移优化是单方向的知识迁移。假设在求解任务Tk时，任务T1,T2,…,Tk-1已经在知识库的协助下得到求解，且求解T1,T2,…,Tk-1获得的有效信息被储存在知识库中［21］，其中，Tk表示为目标任务，T1,T2,…,Tk-1表示为源任务。STO 基本流程如图1所示，STO 利用来自源任务的知识提升求解目标任务的EA 性能。

图1 STO 基本流程Fig.1 Basic procedure of STO

1.2 多任务优化

多任务优化将当前所有同等优先级任务之间的有效信息共享，实现全方位知识迁移。MTO 基本流程如图2 所示，任务T1,T2,…,Tk同时被优化，优化过程中得到的有效信息在公共知识库中不断更新并共享。

多任务优化算法解决的k个任务既可以是单目标优化问题（Single-objective Optimization Problem，SOP），也可以是多目标优化问题（Multi-objective Optimization Problem，MOP）。假设任务的目标函数及其搜索空间分别为fk和Ωk，则MTO 的定义如式（1）所示，MTO 的目标是找到每个任务的最优解［29］。

截至目前，实现进化多任务优化的范式有两种：第一种是采用单个种群搜索多个任务的最优解，称为单种群多任务优化（Single-population based Multitasking Optimization，SMO），多因子优化为SMO 的一种具体实现［33］；第二种是为每一个任务分配一个种群来搜索各自最优解的范式，称为多种群多任务优化（Multi-population based Multitasking Optimization，MMO），生物群落共生进化算法为MMO 的一种具体实现［34］。

目前，在进化多任务优化算法中的知识迁移模式分为隐式知识迁移和显式知识迁移。隐式知识迁移通过EA 的交叉算子实现不同任务种群间的知识交流，多数基于多因子优化范式的算法采用隐式知识迁移，例如多因子进化算法（Multifactorial Evolutionary Algorithm，MFEA）。显式知识迁移是将一个任务完整的解决方案迁移到另一个任务的EA 中，在基于MMO 范式的算法中比较常见［35］。除此之外，显式知识迁移也可以通过映射函数将源任务的解决方案映射到目标任务的搜索空间中［36］。

1.3 多形式优化

多形式优化的基本思想是将不同的替代公式组合成一个求解单目标优化问题的算法，避免了单一公式的缺陷。MFO 基本流程如图3 所示。假设组合算法f含有k个替代公式f1,f2,…,fk，则MFO 的定义如式（2）所示，MFO 的目标是通过f1,f2,…,fk找到任务T的最优解。

图3 MFO 基本流程Fig.3 Basic procedure of MFO

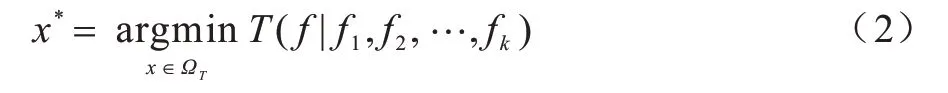
其中：ΩT为T的搜索空间。

2 进化迁移优化算法

本节从源任务选择、知识迁移、缩小搜索空间差异、进化算法搜索、进化资源分配等5 个角度对ETO算法进行综述。

2.1 源任务选择

在进化迁移优化算法中，为目标任务选择合适的源任务是知识迁移成功的关键。合适的源任务可以促进知识正向迁移，提升目标任务的优化效率。不合适的源任务会造成知识负迁移，对目标任务带来负面影响。一些学者认为选择源任务的关键指标是其他任务和目标任务的相似度。某个任务与目标任务的相似度越高，该任务越适合作为源任务。基于任务相似度的源任务选择方法基本流程如图4 所示。一种计算任务相似度的方法是测量任务解的分布差异。文献［37］提出一种基于相似历史信息迁移的骨干粒子群优化算法。该算法结合最大均值差异（Maximum Mean Discrepancy，MMD）和聚类算法提出一种基于多分布估计的最大均值差异指标来评价历史任务和新任务解的分布差异，显著提高了EA的收敛速度和搜索效率。另一种计算任务相似度的方法通过构建任务解的混合概率模型实现。文献［38］介绍了任务解的混合概率模型与任务相似度的关系。每个源/目标任务概率模型代表一个任务的高质量解组成的种群。混合概率模型为每个概率模型的加权和，概率模型的加权系数越大，源任务与目标任务间的互补性越强。基于该理论，文献［38］提出一种基于自适应模型的迁移优化框架，首先建立源任务和目标任务的统一搜索空间，然后在统一搜索空间中利用求解源任务和目标任务获得的知识建立混合概率模型来计算源任务和目标任务的相似度。该方法在SOP 和MOP 上均取得了较好的结果。文献［39］证明了文献［38］提出理论的正确性，并进一步证明了在混合概率模型中增加源任务概率模型的数量可缩小父代种群和子代种群的分布差异。

图4 基于任务相似度的源任务选择基本流程Fig.4 Basic procedure of source task selection based on task similarity

不同于以上根据任务相似度选择源任务的方法，一些学者根据演化过程中其他任务的知识在目标任务上的反馈来选择源任务。文献［40］提出一种基于信用分配的自适应源任务选择机制，在演化过程中为目标任务提供更多有利于解决方案的任务，获得更高的知识迁移概率。

然而，一些学者认为仅根据任务的相似度或其他任务的知识迁移到目标任务后的反馈这种单一标准选择源任务是不合适的，应该将两者结合，综合选择源任务。文献［41］提出一种基于高效代理辅助模型的多任务进化框架。首先利用协方差矩阵来表征任务历史解的分布特征；然后计算不同任务协方差矩阵间的Kullback-Leibler 散度（Kullback-Leibler Divergence，KLD）来代表任务间的相似度；最后结合任务的相似度，利用基于信息素的协同搜索机制为目标任务选择最合适的源任务。文献［42］介绍一种多任务进化算法框架，并提出一种自适应选择机制，通过种群进化过程中知识迁移积累的奖励动态调整目标任务选择其他任务作为源任务的概率，结合目标任务与其他任务的相似度来选择源任务，同时采用档案来记录不同任务在演化过程中的相关信息，根据档案中存储的信息计算不同任务解的KLD 作为任务间的相似度。

2.2 知识迁移

在为目标任务选择合适的源任务后，下一步就是任务间的知识迁移。学者们从多个角度对知识迁移策略进行设计。一些学者认为知识迁移策略需要与解决的问题类型相匹配，应该根据问题的特点设计知识迁移策略。例如动态优化问题，全局最优解会在优化过程中动态变化，即不同时间段的目标任务不同，因此解决动态优化问题的关键是如何为不断变化的目标任务提供合适的知识。针对连续动态优化问题，一些学者将预测模型与ETO 算法相结合，利用求解历史任务获得的优秀种群个体训练预测模型，在求解新任务时利用预测模型预测出适合求解新任务的种群个体，流程如图5 所示。文献［43］提出一种将EA 与时间序列模型相结合的种群个体位置预测模型。该模型利用历史任务的最优解序列作为构建预测模型的知识。当检测到目标函数发生变化时，预测出适合新任务的种群个体的位置。该方法在目标函数变化频率较高的动态多目标优化问题中取得了较好的效果。文献［44］提出一种基于回归迁移学习的预测算法。该算法利用求解历史问题得到的种群构建回归预测模型，为求解新问题的EA 生成高质量的初始种群。2020 年至2021 年，该团队在这个方向进行了较多的研究并取得了系列成果。文献［45］提出一种基于内存驱动的流形迁移学习算法。该算法将EA 求解历史任务获得的最佳个体与流形迁移学习的特征相结合。当目标函数改变时，预测适合求解新任务的种群个体，将预测的种群个体与求解历史任务得到的最佳种群个体合并，构成求解新任务的EA 初始种群。该算法显著提高了EA初期的搜索能力，并降低了计算成本。文献［46］定义了动态优化过程的膝关节点。当检测到目标函数变化时，首先将膝关节点输入预测模型获得适应新问题的种群个体，然后采用基于不平衡迁移学习的方法生成新问题EA 的初始种群。该方法提高了EA的收敛速度和计算结果的质量。文献［47］提出一种基于个体迁移的两阶段动态多目标进化算法。第一阶段采用预学习策略生成引导种群来减少负迁移的可能性。第二阶段采用文献［48］提出的算法构建预测模型来产生优良的初始种群。

图5 基于预测模型的知识迁移基本流程Fig.5 Basic procedure of knowledge transfer based on prediction models

在离散动态优化问题的背景下，文献［49］提出一种具有学习能力的新型进化搜索范式来解决动态的车辆路径规划问题。该方法在优化过程的前期从其他相似车辆路径规划问题的解决方案中获取结构化知识，当检测到问题发生变化时利用获取的结构化知识解决新问题，降低了求解新问题的时间成本。文献［50］将遗传规划（Genetic Program，GP）与代理辅助模型结合，提出一种基于遗传规划和代理辅助模型的进化多任务算法。该算法为每个任务分配一个种群和一个代理辅助模型，通过代理辅助模型筛选种群中的优秀个体进入下一代，同时将代理辅助模型筛选出的优秀个体作为结构化知识在任务间进行迁移，提高了任务间知识迁移的效率和GP 的收敛速度。

对于不同领域相关问题间的知识迁移，文献［51］介绍了一种进化模因计算范式，并基于该范式提出一种基于半正定规划的同构迁移学习算法解决同构的带有容量限制的车辆路径规划问题（Capacitated Vehicle Routing Problem，CVRP）和带有容量限制的车辆弧路径规划问题（Capacitated Arc Routing Problem，CARP）。首先构造能够表示源任务空间和目标任务空间共同特征的空间，然后利用半正定规划在共同特征空间中对源任务进行学习，将获得的知识模因存入知识库。当解决新任务时，将知识库中适合新任务的知识模因迁移到新任务的EA 种群中。该方法可以显著提高EA 在CVRP 和CARP 上的搜索能力。文献［52］在文献［51］的基础上提出一种基于半正定规划的异构迁移学习算法来求解异构的CVRP 和CARP。

在单目标和多目标优化背景下，文献［30］提出一种基于决策变量分析的进化顺序迁移优化算法，实现了SOP、MOP 和超多目标优化问题（Manyobjective Optimization Problem，MaOP）之间的知识迁移。将MOP 和MaOP 的决策变量分为收敛性变量和决策性变量，收敛性变量含有源问题的搜索经验，决策性变量含有源问题的搜索分布经验。通过迁移收敛性变量加速目标问题EA 的收敛速度，通过迁移决策性变量增加目标问题EA 的种群多样性。文献［53］证明了将单目标优化问题转化为多目标优化问题后进行求解，可有效降低EA 陷入局部最优解的风险。受文献［53］的启发，文献［32］提出一种单目标和多目标多因子进化算法求解SOP。将SOP 分解为多个子问题，子问题组成MOP。采用MFEA 同时求解SOP 和MOP，将求解MOP 获得的知识迁移到求解SOP 的种群中提升种群的局部搜索能力。文献［54］提出一种多形式多目标进化优化算法求解MOP。通过高斯过程回归构建目标MOP 的辅助任务，利用去噪自动编码器实现目标MOP 和辅助任务间的显式知识迁移。该方法能有效提高EA 种群的收敛速度。文献［55］对多目标优化中的目标约简进行了理论研究，并分析了两种主流的目标缩减方法的优势和劣势。将目标缩减视为多目标搜索问题，介绍了该问题的3 个多目标公式。在此基础上提出一种基于多目标约简的多目标算法求解MOP。将根据目标MOP 构造的3 个多目标公式作为辅助任务，通过目标MOP 与辅助任务的知识交流提升求解目标MOP 的EA 性能。

在复杂优化问题背景下，文献［56］构建一种基于结构迁移的迁移学习框架解决多标记标签单核苷酸多态性选择问题，并提出一种基于树形结构的分布式估计算法（Estimation of Distributed Algorithm，EDA）来提取历史问题中的结构知识，并利用结构知识构造聚合矩阵。当求解新问题时，将聚合矩阵迁移到新问题的EDA 中。该方法能够降低学习EDA概率模型的时间成本，以及获得高质量的计算结果。

除了上述针对ETO 算法解决的问题类型设计知识迁移策略这一研究方向，一些学者对演化过程中知识迁移的频率或知识迁移的交叉算子等固定参数进行自适应设计。文献［57］通过理论分析证明了知识迁移率对MFEA 的性能有较大的影响，合适的知识迁移率可以提升种群的收敛速度。基于该理论，文献［58］提出一种显式多种群进化框架。首先计算通过知识迁移获得的优于父代的子代个体数与父代个体数的比例，然后根据该比例自适应调整知识迁移的频率。该方法有效抑制了负迁移的影响。文献［59］提出一种基于自适应知识迁移的MFEA。该方法根据演化过程中获得的知识迁移信息自适应选择知识迁移的交叉算子，实验结果表明其显著优于MFEA。

2.3 搜索空间差异缩小

在进行任务间知识迁移时，如果源任务和目标任务的搜索空间相差较大，则需要考虑从源任务中迁移到目标任务的知识是否能够适应目标任务的搜索空间，否则会造成知识负迁移。为了减少源任务和目标任务搜索空间的差异，学者们提出了一系列方法。一些学者通过设计搜索空间映射函数将求解历史任务获得的优秀种群个体映射到目标任务的搜索空间。本文以旅行商问题（Traveling Salesman Problem，TSP）来描述搜索空间映射的基本流程。如图6 所示，源任务和目标任务均为含有6 个城市点的TSP，首先根据源TSP 和目标TSP 的城市点坐标学习两者的映射关系，获得映射函数M。例如，图6 中源TSP 中的城市点S1与目标TSP 中的城市点T3间有映射关系，S1通过M映射到目标域后转换为T3，然后将源TSP 的最优解通过M映射到目标TSP 的搜索空间中，与求解目标TSP 的EA 种群合并。文献［60］提出一种基于单层去噪自动编码器的进化搜索范式。该方法将历史问题的知识通过单层去噪自动编码器映射到新问题的搜索空间中，有效提升了异构问题间知识迁移的效率。文献［61］对文献［48］提出的算法缺陷进行分析，提出文献［48］算法的改进版本。将EA 求解历史任务获得的种群个体通过线性核映射到新任务的搜索空间中作为新任务的EA 的初始种群。文献［36］提出基于子空间对齐和自适应差分的多目标多任务进化算法。首先将源任务的数据和目标任务的数据输入子空间对齐策略中生成映射矩阵，然后通过映射矩阵将源任务中的解映射到目标任务的搜索空间。

图6 搜索空间映射基本流程Fig.6 Basic procedure of search space mapping

与上述通过设计搜索空间映射函数减少源任务和目标任务搜索空间差异的研究不同，文献［62］提出一种决策变量翻译策略。该策略将不同任务搜索空间中的解映射到统一的搜索空间中，减少了知识迁移时来自不同任务个体的位置差异。文献［63］提出一种基于线性化领域自适应的进化多任务算法。该算法将简单任务的搜索空间转换为与复杂任务高度相关的重构空间，以减少简单任务和复杂任务搜索空间的差异。

2.4 进化算法搜索

在ETO 算法中，EA 搜索目标任务最优解的过程可以分为两部分：一部分是利用从源任务迁移到目标任务的知识引导EA 种群进行搜索；另一部分是目标任务EA 种群的进化搜索。上文介绍的策略均以通过提高知识迁移的效率来提升EA 的性能，而本节介绍的搜索策略旨在通过为EA 设计新的搜索算子［64］、将EA 中的某些固定参数改造成自适应参数［65］，以及针对特定问题为EA 构造搜索空间［66］等策略提升EA 种群的搜索能力，从而提升目标任务的优化效率。

一些学者利用代理模型来提升EA 的搜索能力。文献［67］提出一种基于多问题代理的迁移进化多目标算法。该算法利用历史问题或正在被优化的问题的模型知识和目标问题的模型知识构建多问题代理模型来增强目标问题上的EA 的搜索能力。该算法在测试函数寻优、复合材料制造和机器学习模型超参数自动调优等问题上的搜索能力显著优于文献［68］提出的算法。文献［69］提出一种基于代理辅助模型的多任务模因算法。该算法为每个任务分配一个种群，种群的进化操作由3 个部分组成。首先利用DE 搜索任务的全局最优解，其次利用具有高斯过程的代理模型预测适合目标任务的种群个体，最后利用协方差矩阵自适应进化策略进行局部搜索。

一些学者通过设计新的搜索策略来提高EA 的搜索能力。文献［70］提出一种基于遗传变换策略和超矩形搜索策略的多因子进化算法。遗传变换策略通过构造的任务映射向量将源任务的父代个体映射到距离目标任务的父代个体较近的位置上。基于对立学习的超矩形搜索策略旨在对每个任务的统一搜索空间和子空间进行高效的搜索和开发，使种群能够搜索到更多的未探索区域。

一些学者针对ETO 算法解决的问题类型设计搜索策略。针对离散动态优化问题，文献［71］提出一种基于GP 的进化多任务算法。该算法为每个任务分配一个种群，通过交叉算子实现任务间结构化知识的迁移，在求解同构和异构的动态柔性车间调度问题时均能获得高质量的解。针对复杂的双层优化问题，文献［72］将TO 与文献［73］提出的基于协同进化分解的双层组合优化算法相结合，提出一种基于TO 的双层组合优化算法。该算法通过协同进化策略提升EA 的全局搜索能力，在求解新问题时，利用从历史问题中获得的知识模因来指导EA 进行搜索，在求解供应链管理中的双层生产分配问题上的表现优于文献［73］提出的算法。

上述研究均是在传统搜索策略的基础上进行改进，文献［74］则是对DE 中的多个传统搜索策略进行理论研究，旨在选出最适合EMTO 算法的搜索策略。在参考文献［75-77］后，文献［74］提出一种通用的多任 务DE框架，包括DE/rand/1/bin、DE/best/1/bin 和DE/current-to-best/1/bin 这3 种传统的DE 搜索策略，并通过设计对照实验验证3 种传统DE 搜索策略的性能。通用的多任务DE 框架如图7 所示。

图7 多任务DE 框架Fig.7 Multitask DE framework

2.5 进化资源分配

在种群演化过程中，知识迁移并不总是有效的。当任务间的知识迁移对算法性能的提升小于种群的进化搜索对算法性能的提升时，应该将更多的进化资源分配给种群的进化搜索。反之，应把更多的资源分配给任务间的知识迁移。基于这一思想，文献［78］提出一种进化资源分配机制。当任务间的知识迁移产生负面影响时停止知识迁移，将进化资源全部分配给求解任务的EA 种群。该机制能够有效平衡任务间和任务内计算资源的分配问题。

在多任务优化背景下，由于不同任务的复杂程度可能不同，在进化资源平均分配给每个任务的情况下，求解简单任务的EA 收敛速度比求解复杂任务的EA 收敛速度快很多。因此，当求解简单任务的EA 已经收敛到一个较好的解时，求解复杂任务的EA 还不能收敛到一个可接受的解。此时进行任务间的知识迁移，会破坏简单任务EA 的收敛性，造成知识负迁移。针对这一问题，一些学者根据任务的计算复杂度为任务分配进化资源，复杂任务可获得更多的进化资源，从而促进求解复杂任务的EA 种群收敛，流程如图8 所示。

图8 基于任务资源动态分配的进化资源分配流程Fig.8 Procedure of evolving resource allocation based on dynamic assignment of task resources

文献［79］提出一种基于动态资源分配策略的进化多任务算法。该算法为每个任务分配一个种群，在每次分配计算资源前计算每个任务种群的进化程度，然后将种群进化程度转换成进化指数。进化指数越低的任务被分配的计算资源越多。该方法能够提升EA 的搜索能力，获得较高质量的解。文献［80］提出一种基于分解和动态资源分配策略的多目标多因子进化算法。该算法将多目标优化问题分解为多个单目标优化问题，使用单个种群同时求解所有单目标优化问题。种群在某个问题上的演化速度越快，分配给该问题的进化资源越多。该方法的整体性能优于文献［81］提出的算法。

2.6 进化迁移优化算法总结

ETO 算法总结如表1 所示，对源任务选择、知识迁移、缩小搜索空间差异、进化算法搜索和进化资源分配等5 个研究方向中提出的核心策略进行整理汇总，并分析它们的优劣势。

表1 ETO 算法的核心策略和优劣势分析Table 1 Analysis of the core strategies and advantages and disadvantages of the ETO algorithms

3 主要挑战和未来研究方向

尽管进化迁移优化算法在进化计算领域取得了巨大的成功，但仍处于初步探索阶段，在理论研究、算法设计和工程应用方面仍有许多潜在的研究方向。通过中国知网（China National Knowledge Infrastructure，CNKI）和Web of Science（WOS）对2014 年至2021 年发表的ETO 论文进行检索，其中CNKI 检索关键词为“进化迁移优化”、“进化迁移学习”、“进化知识迁移”、“进化多任务优化”和“知识模因”。WOS检索关键词 为“evolutionary transfer optimization”、“evolutionary transfer learning”、“evolutionary knowledge transfer”、“evolutionary multitask optimization”和“knowledge memetic”。通过对文献进行数据清洗，包括文献合并除重、补全缺失信息及去除领域不相关文献，最终得到41 篇中文文献和180 篇英文文献。2014 年至2021 年CNKI 及WOS 的ETO 论文数统计如图9 所示，可以看出ETO相关论文发表数量在2018 年后增长迅速，ETO 在近几年已成为研究热点。

图9 2014 至2021 年的ETO 论文数统计Fig.9 Statistics of ETO papers from 2014 to 2021

本文运用知识图谱对ETO 相关论文进行数据挖掘、信息处理、知识计量和图形绘制，揭示ETO 的发展趋势，从而根据ETO 发展趋势和经验分析得出ETO 未来研究方向和每个方向面临的挑战。通过文献关键词搜索和聚类，对ETO 研究热点分布进行可视化，图10 为基于CNKI 的中文论文研究热点分布，图11 为基于WOS 的SCI 英文论文研究热点分布。在图10 和图11 中：圆表示关键词，圆的大小表示关键词出现的频次；连线表示节点与节点间曾经共现过；连线的密集程度表示该研究主题与其他主题联系的紧密程度。通过对知识图谱的分析，挖掘出ETO 未来研究方向：

图10 CNKI 关键词共现分析Fig.10 Co-occurrence analysis of CNKI keywords

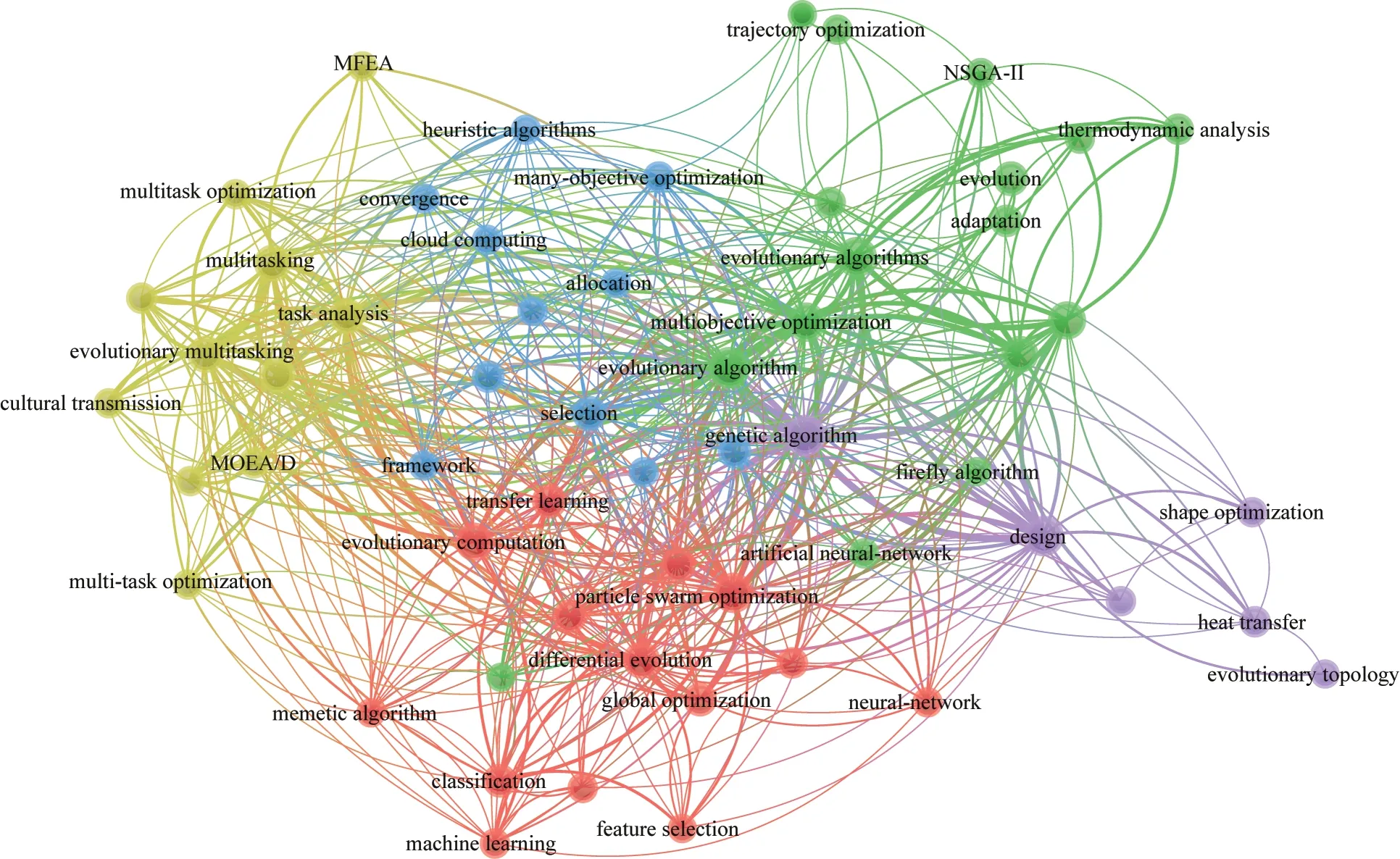
图11 WOS 关键词共现分析Fig.11 Co-occurrence analysis of WOS keywords

1）多目标优化为当前最热门的研究领域，在该领域中一些学者将研究重点放在如何提升任务间知识迁移的效率上，例如文献［30，54-55］。为目标任务选择合适的源任务是知识迁移成功的关键之一，而任务间的相似度是选择合适任务的重要标准。目前还没有能够全面精确计算任务间相似度的方法，因此设计精准的相似度度量方法可作为未来研究方向之一。除了任务选择方法，如何将源任务提供的知识转换成适合目标任务搜索空间的知识也是知识迁移成功的关键，学者们对于该方向的研究多数基于同构问题，对异构问题间的知识迁移研究较少，例如SOP 与MOP 间的迁移、MOP 与MaOP 间的迁移，因此设计跨异构问题知识迁移的有效方法可作为未来研究方向之一。在该领域中还有一部分学者对如何提升ETO 算法的搜索能力和优化速度进行研究，如文献［67，70］。虽然学者们在该方向上取得了巨大的成功，但是他们所解决的问题类型主要是中小规模优化问题，对于含有大量数据或决策变量的大规模优化问题，他们设计的算法可能会失效，因此开发解决大规模优化问题的ETO 算法也可作为未来的一个研究方向。

2）多形式优化是一种新兴的迁移优化范式，在知识图谱中还未出现与“多形式优化”和“multiform optimization”相关的关键词，说明学者们对于设计基于多形式优化的ETO 算法的研究极少，因此基于多形式优化的ETO 算法是一个具有较大发展潜力的研究方向。

3）从知识图谱中可以看出学者们在连续优化问题上的研究较多，在离散优化问题上的研究较少，如果能将针对连续优化问题提出的有效ETO 算法和理论转译成适合求解离散优化问题的ETO 算法和理论，则会极大地促进ETO 算法在离散优化领域的发展，对发电调度、物流配送和无人机路径规划等实际离散优化问题的求解具有借鉴作用。同样地，将针对离散优化问题提出的ETO 算法和理论转译成适合求解连续优化问题的ETO 算法和理论，会对从事连续优化领域相关工作的学者提供启发。因此，如何将连续优化理论与离散优化理论进行相互的转译可作为未来的一个研究方向。

基于以上分析，本文确定求解大规模优化问题的ETO 算法设计、跨异构问题知识迁移的有效方法设计、基于多形式优化范式的ETO 算法设计、精准的相似度度量方法设计和连续与离散优化问题的理论转译等5 个ETO 未来研究方向，下面将对这5 个未来研究方向和研究方向中存在的挑战进行详细叙述。

3.1 大规模优化问题求解

目前，利用进化算法求解大规模优化问题的研究越来越多，例如利用EA 求解激光雕刻［82］、物流调度［83］和车辆路径规划［84］等问题。由于大规模优化问题含有大量的数据或决策变量，EA 求解此类问题时无法在可接受的时间内搜索到较高质量的计算结果。为了提高EA 求解大规模优化问题的性能，学者们提出了不同的方法，例如采用“分治”的思想将大规模优化问题分解为许多适合EA 求解的小规模优化问题分别求解［85-86］，以及设计新的搜索算法［87］等。与以上方法相比，ETO 为提升EA 求解大规模优化问题的性能提供了新思路，正如前文所述，问题很少孤立存在，将EA 求解中小规模优化问题获得的知识迁移到相似的大规模优化问题来指导EA 的搜索过程，有助于提升EA 的搜索能力，从而提升计算结果的质量。具体研究思路为：1）将ETO 和“分治”思想相结合，在利用“分治”思想将大规模优化问题分解成许多小规模优化问题后，采用ETO 算法实现多个小规模优化问题的知识迁移；2）设计能够将中小规模优化问题中的知识高效迁移到大规模优化问题搜索空间中的方法。

3.2 跨异构问题的知识迁移

目前，一些学者已经实现了跨异构问题的知识迁移，例如文献［30，71］实现了单目标优化问题和多目标优化问题间的知识转移，文献［60］采用去噪自编码器作为异构问题间知识迁移的桥梁，将源问题的解映射到目标任务的搜索空间中。但是，在MOP领域，目前的跨异构问题知识迁移方法多数忽略了任务之间的关系［88］。从种群共生方式的角度看，存在3 种方式：第一种方式是共生，不同种群之间相互合作、互惠互利，对所有种群均带来积极影响；第二种方式是寄生，不同种群共同生活，既有积极的影响，又有消极的影响；第三种方式是竞争，不同种群之间相互竞争，对所有种群均带来消极影响。同时，任务关系也可以解释为共生、寄生和竞争［54］，假设任务1 是三目标优化问题，任务2 是两目标优化问题，两个任务的Pareto 最优解集在目标函数空间的投影不同，任务为竞争关系，一个任务的改善会导致另一个任务的恶化［89］。该领域面临的另一个挑战是当源问题与目标问题维度差距过大时，现有的知识迁移方法往往会失效。具体研究思路为：1）设计考虑任务间关系的跨异构问题知识迁移方法；2）设计能够有效解决维度相差较大问题间知识迁移的方法。

3.3 多形式优化范式

多形式优化是近期提出的新迁移优化概念，基本思想是将不同的替代公式组合成一个求解单目标优化问题的算法，避免了单一公式的缺陷［90］。由于不同的替代公式代表不同的搜索策略，在多任务环境中，每个公式都可以作为辅助任务将自身的搜索经验传递给其他任务，因此在该环境下的多形式优化范式面临的一个巨大挑战是如何有效地跨不同公式进行知识迁移。由于EA 的种群个体和种群移动轨迹中包含搜索经验，因此可以将EA 作为实现不同公式间有效知识迁移的媒介引入多形式优化中，利用源任务种群存储的搜索经验来指导目标任务的EA 的搜索过程。此外，多形式优化面临的另一个挑战是由于计算资源的限制，难以确定哪个公式最适合求解当前的问题。具体研究思路为：1）设计能够针对特定问题自适应选择替代公式的ETO 算法；2）设计可以实现跨异构问题知识迁移的方法，例如在高维度问题和低维度问题之间进行知识迁移。

3.4 相似度度量

在进化迁移优化算法中，为目标任务选择合适的源任务是知识迁移能否成功的关键，任务间的相似度是选择源任务的重要依据。当前度量任务间相似度的方法大致可以分为两类：第一类是利用源问题和目标问题的数据样本分布的差异来衡量任务间的相似度，例如文献［37］计算源问题解和目标问题解的MMD，利用MMD 衡量任务间的相似度；第二类是利用源问题和目标问题解分布的差异来衡量任务间的相似度，例如文献［41-42］将源任务和目标任务解分布的KLD 作为任务间的相似度。然而以上两类方法均没有考虑到求解不同任务的EA 种群进化方向的相似性，在忽略迁移时机是否恰当的情况下，当种群进化方向不相似时，很可能造成负迁移［88］。具体研究思路为：1）针对特定问题设计特定的任务相似度度量方法；2）研发新的衡量任务相似度的指标。

3.5 连续与离散优化问题的理论转译

目前，多数进化迁移优化理论均是基于连续优化问题背景或离散优化问题背景提出的，将适用于连续优化问题的进化迁移优化理论与适用于离散优化问题的理论互相转译，可有效促进ETO 在连续优化领域和离散优化领域的发展，一些学者在该方向进行了研究，例如文献［91］将文献［92］中的MFEAII 算法包含的理论转译成了适合求解离散优化问题的理论，提出dMFEA-II 算法来求解TSP。然而，据笔者所知目前在该方向的研究很少，阻碍该方向发展的主要挑战是适用于连续优化问题的ETO 算法中所包含的一些理论只适用于连续型数据，缺少与之对等的适用于离散型数据的理论。具体研究思路为：1）设计求解连续优化问题的ETO 理论的离散型版本；2）开发测试转译后的算法性能的基准问题。

4 结束语

本文从源任务选择、知识迁移、缩小搜索空间差异、进化算法搜索和进化资源分配等研究方向入手，对现有进化迁移优化算法进行归纳总结。通过分析5 个研究方向的核心策略和优劣势得出，ETO 算法在搜索能力和收敛速度上相比于传统EA 具有一定优势。后续将对利用ETO 算法高效求解大规模优化问题、实现异构问题的高效知识迁移、多形式优化范式的研发、精准的相似度度量方法设计以及连续与离散问题的理论转译等方面做进一步研究。