稳定性同位素营养级估算的差异性与影响因素
——以鲢鳙为例
2023-01-19白子晗王睿龙王康
白子晗,王睿龙,王康
1.华中农业大学生命科学技术学院, 武汉 430070; 2.中国科学院水生生物研究所/淡水生态与生物技术国家重点实验室, 武汉 430072
稳定性同位素技术因对生态系统的影响小,能很好地反映生态系统中的能量流动和物质循环,被广泛应用于记录生态系统的特征和过程,如物种的饮食结构、营养位置、资源获取和分配模式及生态位特征等[1]。其中,营养级代表生物在食物网中所处的地位,可以用于分析食物网中食物链长度、能量流动方向和杂食程度等[2],并逐渐成为了评估、检测生态系统动态、生物多样性变化的重要指标[3]。在2种常用的同位素标记(δ15N、δ13C)中,δ15N在捕食者与猎物之间一般体现为明显且有规律的富集(通常为0.3%~0.4%),所以经常用来估算消费者的营养级;而δ13C随营养级升高变化不大,当碳源的同位素特征不同时,可以用来评估不同营养来源的比例[4]。最简单的营养级计算模型需要首先确定出基准生物的营养级λ以及它的δ15N值,再获取目标生物的δ15N值和相邻营养级之间的氮富集系数[5]。另外,考虑到消费者会从不只一种能量来源中获取N元素,因而引入δ13C标记来估算不同营养来源的比例,从而构建出双基准的稳定性同位素混合模型[4]。但是上述的简单模型和混合模型的计算方法仍存在很多局限性,在模型的假设中,N的营养歧化因子(trophic dis‑crimination factors, TDF)通常取定值0.34%,而C则被假定几乎不发生营养歧化。但实际上,TDF值会受到如食物摄取率、发育阶段、性别、体质量等[6]多种因素的影响。因此,简单和混合模型等传统计算方法中对个体之间的变异的忽略可能会在估算营养关系时造成很大的误判。
另外,传统算法的估算结果往往会受到样品采集质量的影响。在试验设计中,每个样点的采样个数一般为10~20。低于这个标准可能会导致数据的离散程度增大,结果的准确性降低,同时也无法反映出消费者营养级连续、线性的变化过程。除此之外,基准营养级在时间和空间上存在变异性,最终会通过食物链作用,影响生态系统中所有营养级生物的同位素特征[2]。
贝叶斯算法作为一种高效、便捷的计算方式,能在模型建立和参数后验估计中引入个体变异性和抽样误差[7],从而克服了传统营养级计算方法的很多局限。但是对于其是否能改善低样本数情况下传统算法的计算结果,提高其准确性,弥补在试验设计上的问题,还需要进一步的探索。
本研究以鲢(Hypophthalmichthys molitrix)、鳙(Hypophthalmichthys nobilis)2种滤食性鱼类作为研究对象。鲢、鳙具有简短且清晰的食物链,广泛分布于我国各个流域,了解其不同区域的营养级状况对整个生态系统有重要的意义。国内外对鲢、鳙的食性、营养级都有一定程度的研究,目前主流观点是鲢的食性偏向浮游植物,而鳙更偏向浮游动物。受食物来源营养等级的影响,鲢、鳙营养级一般在2~3之间波动,且鳙略高于鲢(图1)。二者基于食物来源的丰度,改变摄食浮游生物的比例,以达到共存的状态[8]。目前已有部分研究基于稳定同位素技术对鲢、鳙的营养级进行了估算,但仅使用了上述的简单和混合模型等传统算法,尚无通过广义贝叶斯算法对鲢、鳙营养级估计的研究。因此,本研究利用贝叶斯算法,对已发表文献中鲢、鳙的营养级进行重新估算,拟探究传统算法与贝叶斯算法结果的差异性,分析营养级估算的变异性与影响因素,以期为今后稳定同位素估算营养级的研究提供理论参考。
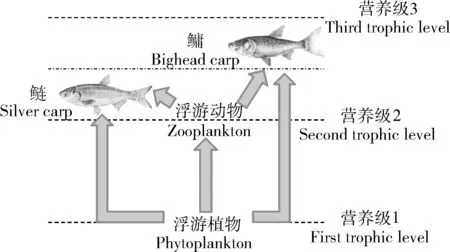
图1 鲢、鳙在浮游食物网中相互作用的示意图Fig. 1 Schematic illustration of trophic interaction in a pelagic food web dominated by silver carps and bighead carps
1 材料与方法
1.1 数据搜集
2019年10月利用中国知网,搜索模式设为“全文”,搜索关键词“鲢”“鳙”“稳定同位素”“食物网”“营养级”,共搜集了15个样点的鲢、鳙、基线(base‑line)三类的δ13C、δ15N同位素数据及其辅助数据;基线分为初级生产者和初级消费者两大类。初级生产者:颗粒有机物(particulate organic matter,POM)、藻类(algae);初级消费者:河蚬(Corbicula flu⁃minea)、东北田螺(Viuiparus chuiYen)、铜锈环棱螺(Bellamya aeruginosa)。辅助数据包括样本采集个数、样点水体的总磷(TP)、总氮(TN)等环境数据,环境数据通过检索与原文献相同采样时间和地点的文献获得。样点主要分布在长江流域、太湖流域、钱塘江流域,包括万州(30°48'N,108°24'E)、养鹿(31°5'N,108°34'E)、双江(30°57'N,108°40'E)、高阳(31°5'N,108°41'E)、黄石(31°00'N,108°43'E)、宜昌(30°40'N,111°19'E)、荆州(29°47'N,112°55'E)、城陵矶(29°26'N,113°9'E)、鄂州(30°27'N,114°51'E)、湖口(29°45'N,116°14'E)、千岛湖(29°33'N,118°57'E)、老虎潭(30°40'N,119°57'E)、太湖(31°16'N,120°7'E)、淀山湖(31°6'N,120°57'E),以及小兴凯湖(45°20 'N,132°34'E)。
1.2 数据处理
对搜集到的数据进行整理,表格数据直接录入Excel,图形数据经过GetData Graph Digitizer软件提取后录Excel。当基准是初级生产者时λ值应为2;当基准是初级消费者时λ值应为1。检查原文献中的计算结果,对基准类型与λ值不对应的情况进行更正。通过软件R(version 4.0.0)中tRophicPosition包对鲢、鳙以及基线生物的同位素数据进行处理,处理后生成营养级,所有数据总结于表1。
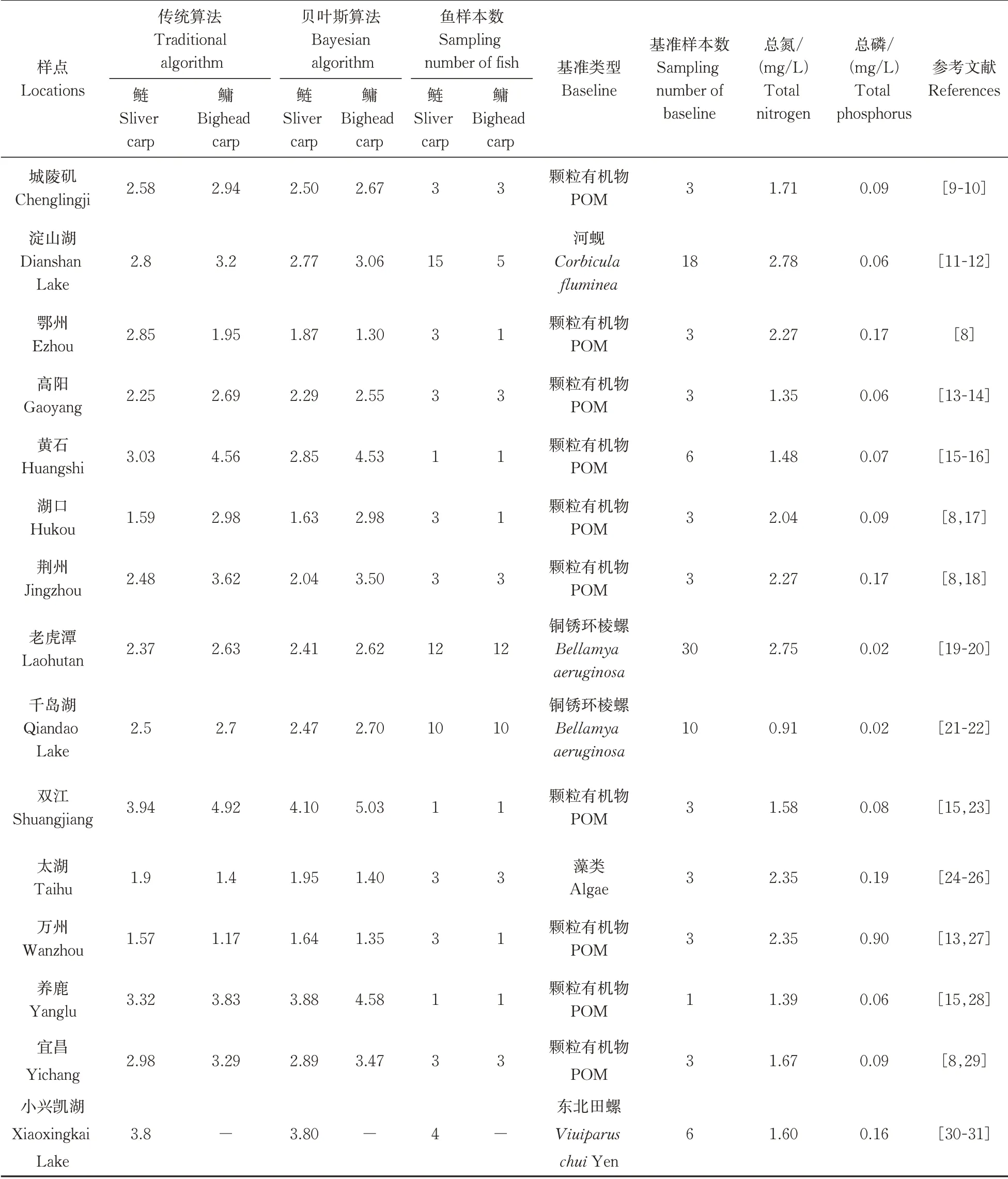
表1 研究数据汇总与文献来源Table 1 Summary of information about silver carp and bighead carp
1.3 数据整理分析
使用分位数图(quantile-quantile plot)检验用于配对样本t检验和相关分析的数据是否符合正态分布。采用配对样品t检验对传统算法和贝叶斯算法下的鲢、鳙营养级进行差异性分析;对贝叶斯算法下鲢、鳙营养级后验估计的区间大小(95% CI)分别和鱼样本数、基准样本数进行Pearson相关性分析,并计算相关系数;对贝叶斯算法下鲢、鳙的营养级后验估计的众数和水体环境中TP、TN数据进行Pearson相关性分析,并计算相关系数。选取一次函数、反比例函数、对数函数、指数函数及复合函数等作为候选模型,对贝叶斯算法下后验分布的置信区间范围与采集样本数的相关性进行拟合,使用赤池信息准则(Akaike information criterion,AIC)筛选出最优模型。
2 结果与分析
在所有的15个样点中,鲢的δ15N取值范围在0.759%~1.593%,最大值出现在太湖(1.593%),最小值出现在湖口(0.759%);鳙的δ15N取值范围在0.563%~1.68%,最大值出现在小江流域双江(1.68%),最小值出现在鄂州(0.563%)。
传统算法下鲢的营养级范围在1.57~3.94、鳙为1.17~4.92,最小值和最大值均分别出现在万州和双江;贝叶斯算法下鲢的营养级范围在1.64~4.10,最小值、最大值出现地点与传统算法下一致,鳙的营养级范围在1.30~5.03,最小值出现在鄂州,不同于传统算法,最大值出现地(双江)与传统算法一致。
经检验用于配对样本t检验和相关分析的数据符合正态分布,传统算法下与贝叶斯算法下的鲢、鳙营养级没有显著性差异(分别为P鲢=0.501 7,P鳙=0.897 6,表2)。贝叶斯算法下营养级的95%置信区间大小与鱼采集个数具有显著性负相关(P<0.001***,R=-0.758,表3),与基准采集个数也同样表现出显著性负相关(P<0.01**,R=-0.535,表3)。在水体环境方面,贝叶斯算法下鲢和鳙的营养级与TP、TN等环境指标未表现出显著的相关性(表4)。

表2 贝叶斯算法和传统算法结果的配对样本t检验Table 2 Paired sample t test of bayesian algorithm and traditional algorithm results
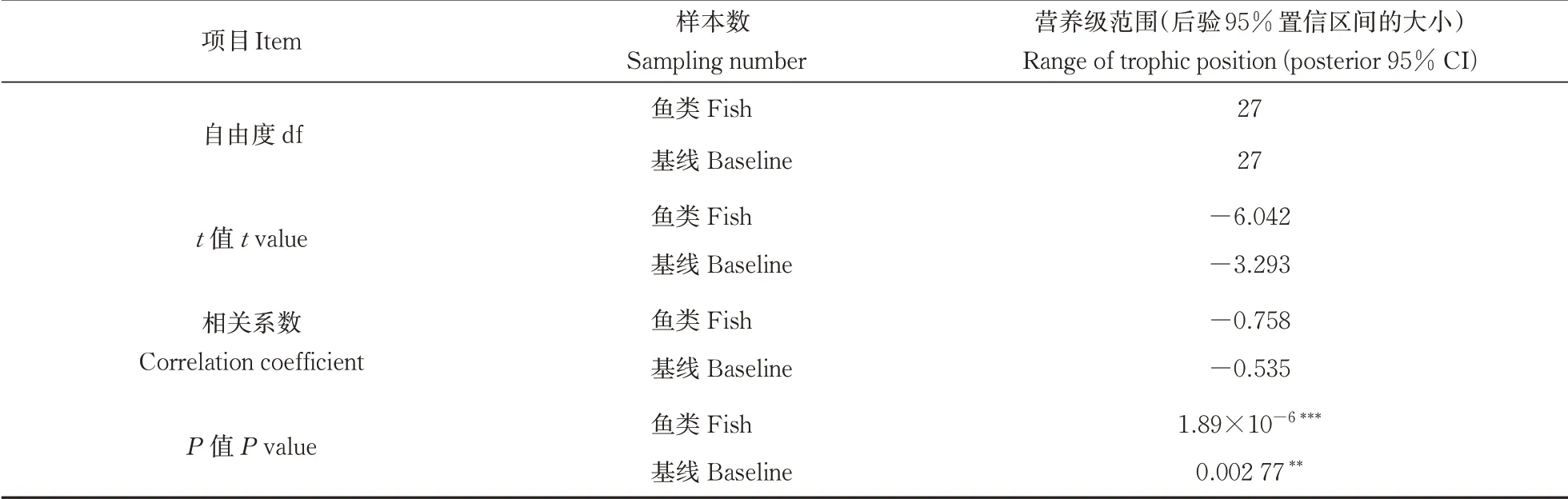
表3 营养级范围与样本数的相关分析Table 3 Correlations between range of trophic positions and sampling number
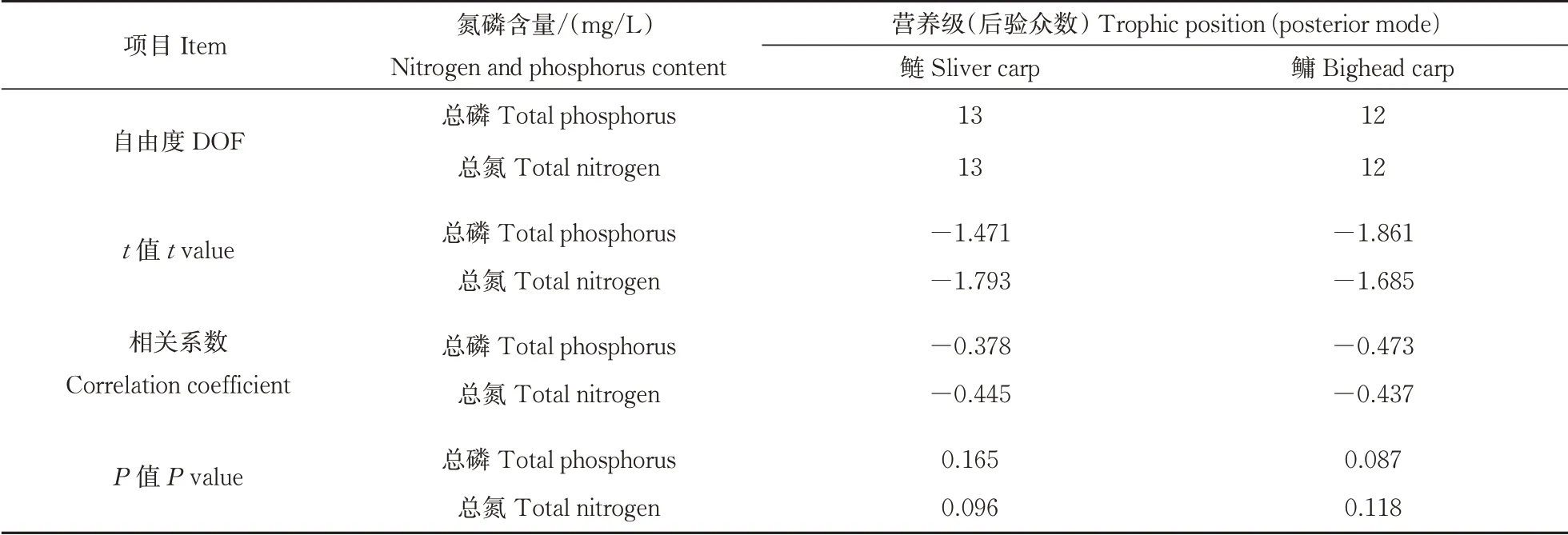
表4 营养级与环境变量的相关分析Table 4 Correlations between trophic position and envionment variables
通过选用不同模型对贝叶斯算法下营养级后验分布的置信区间范围与采集样本数之间的相关关系进行拟合,发现指数函数对观测结果的解释能力最强(AIC=63.676,表5)。根据模拟曲线(图2),与样本数=1时相比,将样本数增加至6,可以使贝叶斯算法下营养级的后验估计的区间大小收敛90%以上。
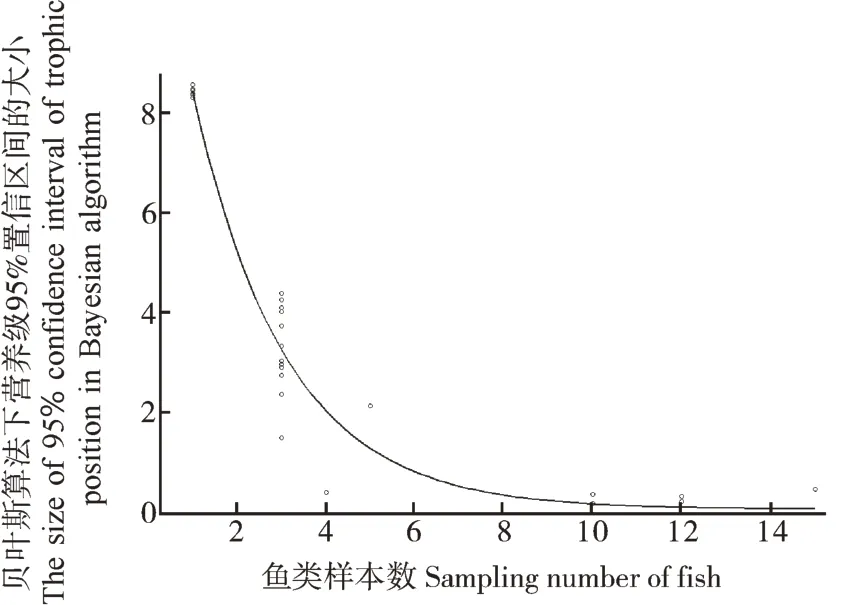
图2 贝叶斯算法中营养级95%置信区间的大小随鱼样本数变化的模拟曲线Fig. 2 Simulation curve of correlation between the size of 95% confidence interval of trophic position in Bayesian algorithm and sampling number of fish
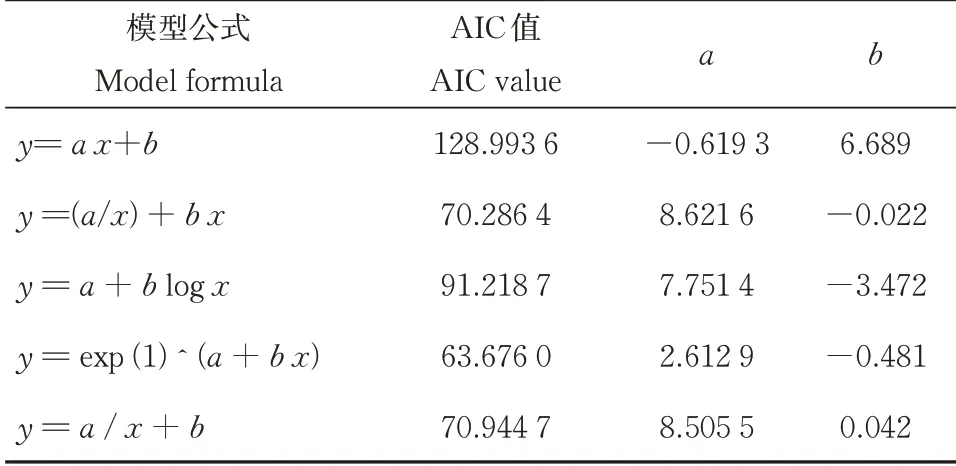
表5 模型拟合信息Table 5 Summary of model fitting information
3 讨论
3.1 贝叶斯算法与传统算法的差异
在2016年武汉东湖的一项试验中显示,主要摄食浮游生物的鲢、鳙营养级的准确范围应该在2~3之间[32],这也是许多研究者公认的,而部分搜集的研究中鲢、鳙营养级与这一结果有较大的偏差。如:本研究中淀山湖、荆州、宜昌样点鳙的营养级超过3;黄石、双江、养鹿样点鲢、鳙的营养级超过3;太湖、湖口、万州鲢、鳙的营养级甚至小于2(表1)。
传统方法计算的鲢、鳙营养级误差较大,而使用贝叶斯算法计算的鲢、鳙营养级与传统方法比较前后无明显差异,说明贝叶斯算法无法提升传统计算方法的结果,或者说即使是利用贝叶斯算法也无法冲淡试验设计对研究结果的影响。
3.2 样品采集对营养级估算的影响
本研究中,贝叶斯算法的置信区间与鱼类和基线的采集样本数目均具有显著相关性,说明采样的强度确实会影响后续分析的结果。在本研究所涉及的15处样点中,除老虎潭、千岛湖、淀山湖外,其他样点采样数量总体偏少,多数为单次采样、无周期性采样,个别样点采样数量为1,如双江、养鹿、黄石,这可能导致了在鲢、鳙营养级估计上的偏差。另外在少数位点,如鄂州、养鹿等,2种算法获得的结果有较大差异。这可能是因为较低的样本量使得传统算法中所依赖的均值和贝叶斯算法所拟合的样本分布之间出现了偏差。而曲线拟合的结果表明,维持采样数在6个以上有助于提高贝叶斯算法的计算结果的准确性。
另外,有10处样点使用了POM进行标定。POM作为一种高周转率的基准,短期或者某一时间点的样品采集分析无法反映出基准作用[33],通常需要分时段、高频率地长期检测,其δ15N值也通常会体现出明显的季节和空间变化。例如,Gu[34]将42个无季节性采样的湖泊和36个进行季节性采样的湖泊进行了对比,发现与进行季节性采样的湖泊相比,无季节性采样的湖泊中POM的δ15N存在持续消耗的现象,而且平均消耗量大于0.2%,甚至可以掩盖浮游动物与POM之间的营养联系。Gu等[35]还发现,在32个研究对象中,POM的δ13C的季节性变化幅度在1%到20%之间,大大超过每次营养转移过程中同位素分馏的水平(<0.1%)。因此在采样期间获取能够反映POM季节性周期变化的样本非常重要,但是本文引用的很多研究仅采集了单次、少量的POM样品,无法满足其作为基准的标准;食物网富集指数也仅采用了定值0.34%[36],这可能是造成其营养级计算误差的一个重要原因。
3.3 水体环境对营养级估算的影响
贝叶斯算法下鲢、鳙营养级与环境因子TN、TP存在相关关系,这说明鲢、鳙所处的水体环境对其营养级具有一定程度的影响。Xu等[37-39]利用稳定碳、氮同位素技术研究了我国东湖、巢湖、抚仙湖等淡水湖泊的水生食物网结构与营养级关系之后,提出外来营养物质输入是导致鲢、鳙、湖鲚等浮游食物网中次级消费者的稳定同位素值升高的原因,这与本研究的结果相似。此外,生态系统的其他组分也受到富营养化的影响,如Gu[34]的研究指出,由于水体营养水平不同,富营养湖泊POM的δ15N的变化幅度(0.26%~2.5%,平均值为1.03%)远大于贫营养湖泊(0.15%~0.85%,平均值为0.42%),因此,水体营养环境对营养级估算的影响不可忽略。
综上所述,稳定同位素技术为研究生态系统各种群之间的能量流动、营养关系提供了新的技术手段,但是该方法的应用还有赖于科学的试验设计和对同位素组成的时间、空间、种内的全面理解,从其结果和采样个数来看,原文献的数据还不能很好地代表目标生物的营养特征,使鲢、鳙的营养级计算结果出现了较大的偏差。为展示研究对象连续、完整、准确的营养特征,今后可展开多月份连续、适当数量的采样,同时还要考虑样点的水体环境的影响。
采样之前,要明确研究整体所代表的时间尺度,基于不同的时间尺度,分析系统中、短期和长期的结构与功能变化也要依据不同检测手段,进行相互补充、相互优化[36]。在研究长期结构时,同位素样品在采样期间需要进行密集采样,每个样点采集10~20个,每月或每2个月采样1次;考虑到高周转率样品同位素的不稳定性,中、短期样品采集个数与采样频率应适当增加,每个样点采集20~30个,每2周采样1次。
