心中有“数”：“童化”视域下学材资源重组建议

2023-01-19单广红

辽宁教育 2023年1期

单广红

（江苏省淮安市白鹭湖小学）

数学知识有着严密的结构体系，数学教师必须要做到心中有“数”，即对数学知识结构能够正确地理解和把握，必须具备扎实的专业素养。北京师范大学郭华教授认为，课堂教学其实是实现“两次倒转”的过程。笔者认为，第一次倒转是“教师理解教材内容”，第二次倒转是“引导学生经历探究过程”。基于“童化”视域的结构化课堂，教师要灵活地对教材资源进行重组，需要前后沟通，领悟教材变化意向；需要灵活变通，梳理内容重组学材；需要对比融通，构建联系编织网络。

一、前后沟通，领悟教材变化意向

教材研读是教师的一项基本功，即实现课堂教学的第一次倒转——教师理解教材内容。在实际教学中，有很多教师对教材编写意图的解读能力比较欠缺，而教材承载着编写专家组赋予的特殊使命，所以，领悟教材中提供的信息内容才能最大化地发挥教材的学科育人价值。

（一）领会术语更换的思想根源

对数学语言的精准解读是数学教师的一项重要基本功，往往教师对教学内容理解到什么高度，基本上就决定了学生所能达到的最高水平。如“解决问题策略—替换”内容，教材修订后变更为“解决问题的策略—假设”。此单元编排了如下的两个例题。

例1：小明把720 毫升果汁倒入6 个小杯和1 个大杯，正好倒满。已知小杯的容量是大杯的，小杯和大杯的容量各是多少毫升？

例2：在1个大盒和5个同样的小盒里装满球，正好是60个。每个大盒比每个小盒多装8个。每个大盒里装了多少个球？每个小盒呢？

编者修订的意图是什么呢？笔者以为，应该不是简单的变换名词。通过用心研读与领悟我们不难发现，“假设”比“替换”更加准确和有创造性，无论是“倍比关系”，还是“相差关系”，替换的目的是统一标准，即“假设标准一样”。这样，教材中的例题就由“二元问题”转化成了“一元问题”。如此来看，“假设”是一种解题策略，“替换”是解题的具体方法。教学中，很多教师“穿着新鞋走着老路”，强调“替换”，关注解题，却忽略了“假设”数学思想的渗透。

（二）感悟内容删减的结构统整

在日常教学中，很多中学教师不了解小学已学了什么，学到什么程度，很多小学教师更不会过问中学将要学什么，是基于什么基础去学习的，这样就形成了“各自为营”的现象。最后，就形成了小学教的内容和方法，中学教师又重新教学，或者用大量时间去返工纠正，缺少“结构化统整”。

《义务教育数学课程标准（2011年版）》指出，用π表示计算的结果，让小学生从繁杂的3.14代替π计算中解放出来。这样，就让中学教师不再为纠正圆周率应用字母“π”表示而恼火。新课标中有一条非常重要的内容调整：把方程从第三学段六年级调整到第四学段七年级，这无疑是对小学教师的又一利好。自从上一轮课改后，解方程的思路由原来的“数量关系式”为主思路，变成“等式的基本性质”为主思路，很多教师以为这下终于可以和中学接轨，花了很大的力气引导学生用“等式的基本性质”解方程。但是，小学生由于受到知识结构的局限，在解决减数或除数作未知数时就遇到了障碍。据了解，中学也并不是用“等式的基本性质”解方程，而是用移项的方法。把中小学教学内容进行结构化安排，既减少了无效重复的劳动，也为中小衔接工作作出了重要贡献。

（三）关注内容增加的现实价值

核心素养导向下的新一轮课改，除了更改或删去原教材中不合时宜的内容，还新增了一项核心素养内容——量感。新课标制定专家有一双“慧眼”，已发现“量感”问题是生活中常见的数学问题，但教师对此内容教学比较弱化，导致学生“量感”的严重缺失。这是教师今后需要研究的一个重要课题，需要教师团队形成合力，对基本的“量与计量”问题，如“厘米”“分米”“米”等长度单位，“平方厘米”“平方分米”“平方米”等面积单位，以及“千克”“克”的质量单位，凡能够亲历体验的内容，一定要创设条件让学生经历，积累准确真实的“表象”经验。而如“千米”“吨”“公顷”等这样大的计量单位，教师就要引导学生走进生活，找到具体的例子，再进行类比、推理，形成自己的间接经验。

二、灵活变通，梳理内容重组学材

“变通”一词出自《周易·系辞》“变通莫大乎四时”。所谓变通，就是依据不同情况，作非原则性的变动。实现课堂教学的第二次倒转——学生经历探究过程，教师要遵循学生的原有认知结构、思维水平以及数学本身的逻辑结构，根据需要，灵活地对学材进行变通重组。

（一）图例呈现形式的微调

教材是学生学习的主要载体，但教材中个别图例相关内容的呈现，是编者理解和想要表达的思维结构，而教师教学时需要分析学情，结合自己的教学思考，进行适当的资源重组。

在教学“万以内数的认识”一课时，教材主题例题选用的是大写的数据呈现——一组农产品产量的主题图（如图1）。

图1

编写思路是从文字符号到数字符号。笔者认为，认识大数，学生通过“读”文字数字是读不出什么数感的，幼儿园的孩子只要识字也可以读出文字来，但只是读文字，对数的大小仍无法识别，而且农业生产离城区的学生生活经验又比较远。所以，笔者对学材进行了重组。重组后，把图例变成了2021年全国第七次人口普查的相关数据（如下页图2），收集了学生比较熟悉的区、市、省人口的近似数，让学生从地域的大小和数位的多少来初步感知人口数的多少。从中学生还能很快调动已有的知识经验，对一长串阿拉伯数字组成的多位数产生强烈的认知冲突和学习需求，想去尝试、去挑战，激发了学习的兴趣。学生在读数、认数中，了解掌握人口数据，为进行当地的生活规划提供了第一手参考数据，体会到了数学学习的现实意义。

图2

（二）内容先后顺序的调换

学习内容的先后顺序并不是一成不变的，教师可以根据学生的学习需要，理顺关系，对教材内容进行结构化重组。

例如，“三角形”的教材单元内容安排顺序依次是：三角形的初步认识、三边关系、内角和、分类。教学“三角形的内角和”验证猜想是否是“180°”时，为了有说服力，应涉及所有类型的三角形，而不应是特殊的少数几个。因此在教学时，笔者调整了教学顺序，将“三角形的分类”调到“三角形内角和”的前一课时。后面在查阅各种版本的教材时发现，绝大多数教材教学内容安排与笔者的观点不谋而合。

（三）课时板块结构的重组

课时内容也需要教师认真、精准地分析，板块要进行结构化设计，要把关联性大的内容划分到一个课时，引导学生类比迁移，这样可以达到事半功倍的效果。

例如，在划分“运算律”单元主题内容课时的时候，个别教师把“加法运算律”划分在一个板块，即加法交换律、加法结合律；把“乘法运算律”划分在一个板块，即乘法交换律、乘法结合律；把乘加混合的单独划分为一个板块，即乘法分配律。这样划分看上去很好，退一步思考，却是不太科学的。“运算律”属于“规律探究”课型，在一节课中，应把规律相似的放在一节课，通过“教结构”“用结构”，通过类比推理，进行“类结构”学习。所以笔者认为，这样设计学习板块更合理一些：把“加法交换律”和“乘法交换律”划分在一板块，引导学生由“a+b=b+a”类推到“a×b=b×a”，并且通过举例使学生发现减法和除法不存在交换律。

同样的道理，教师可把“加法结合律”和“乘法结合律”划分在一个板块，由“（a+b）+c=a+（b+c）”类推到“（a×b）×c=a×（b×c）”；而“乘法分配律”含有两级不同运算，因此可仍然单独设立一个板块。具体单元重组如表1。

表1 运算律：课时板块结构重组

三、对比融通，构建联系编织网络

医学上有句话叫“痛则不通，通则不痛”。学习中的道理也一样，教师的主要教学任务就是引导学生打通困惑点、领悟关键点、捕捉链接点。

（一）对比分析，打通困惑点

学生在学习过程中，常会受到知识“负迁移”的干扰，会产生一些困惑的、纠结不清的问题。这时，教师要在第一时间去指点迷津，帮助学生扫清学习障碍，这样利于学生积累更丰富的学习经验。

例如，在学习了“运算律”后，学生基本能理解五大运算律的意义，并能熟练、正确地选择相应的方法进行简便计算。学生从“加法交换律”联想到“乘法交换律”，又从“加法结合律”联想到“乘法结合律”，构建了加法运算律的知识结构及方法结构，形成了正迁移。由此，学生又从“乘法分配律”想到：是否会存在“除法分配律”呢？在后续的计算中，学生容易“跟着感觉走”，而不小心“入坑”。发现这样的现象后，教师自己先要搞明白——“为什么除法用分配律有时灵，有时不灵呢？”再耐心引导学生理解道理。

例如，“（360+42）÷6”就可以用所谓的“除法分配律”来完成计算：（360+42）÷6=360÷6+42÷6=60+7=67，但“100÷（20+5）”就不能写成“100÷20+100÷5”。这是为什么呢？原来，类似“（a+b）÷c=a÷c+b÷c”，等号左右两边的分配标准没有变，可以变式为乘法来理解；而反过来“a÷（b+c）≠a÷b+a÷c”，因为前后的分配标准被改变了。这样，学生理解了数学道理，就会避开“负迁移”的干扰。

（二）异中求同，领悟关键点

数学问题看似千变万化，但其间好多道理是相通的。教师要引导学生去归纳、发现，使学生领悟数学本质的关键点，进行“类结构”学习。

例如，“行程问题”需要把握三要素：出发点、速度和方向。如图3 所示，教师可先从学生熟悉的两地“相向”而行的典型问题，然后再类推到同时、同地“相背”而行问题和只是方向不同，但都是求路程和问题；从开放路线到封闭路线，把环形跑道沿出发点或相遇点剪开，化曲为直，正好对应着直线的“相向而行”或“相背而行”；从“一次相遇”一个全程，到“二次相遇”行三个全程。这样异中求同，循序渐进，借助线段图或动态演示帮助学生理解领悟。

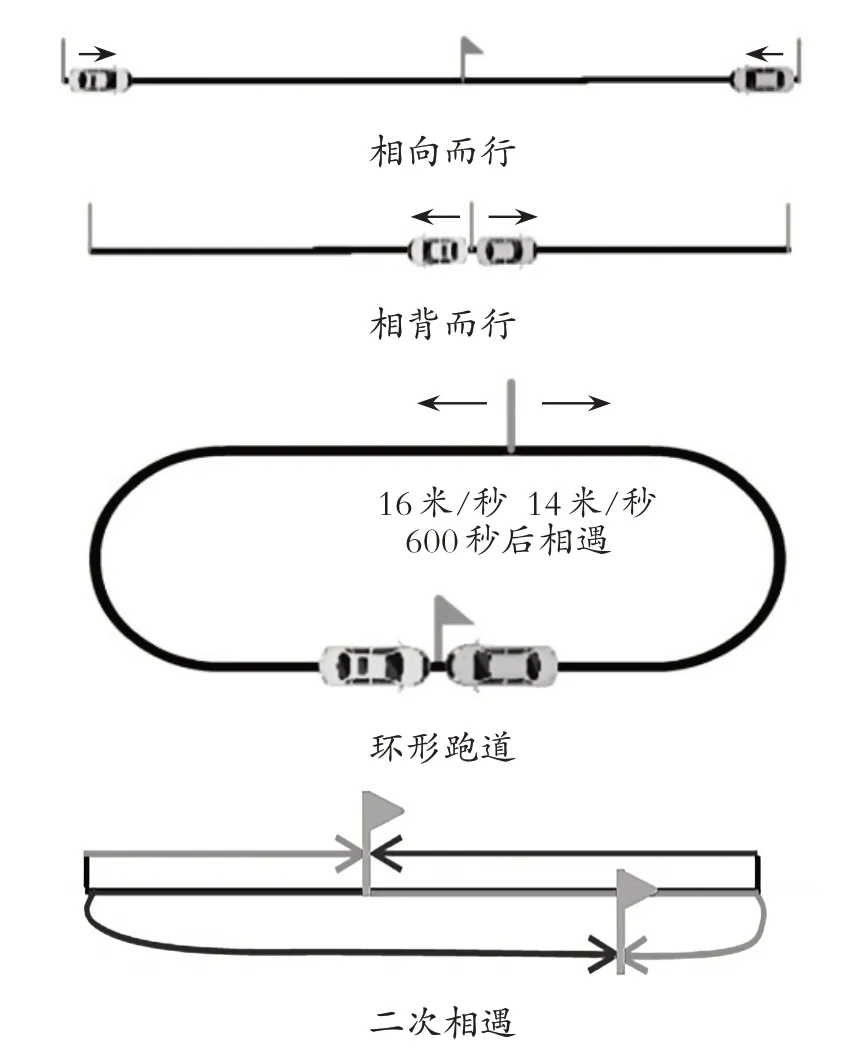
图3

（三）同中求异，捕捉链接点

有些数学问题看似相同，但是其中一些细微的变化学生不容易发现，这时就需要教师引导学生斟词酌句，同中求异，发现其中的规律。

例如，“植树问题”可分为三种情况：两头都不植、两头都植、一头植一头不植。教学时，教师要整体引入，让学生既见“树木”，又见“森林”。有位教师这样设计了两个活动。

活动一：五（1）班每隔5 米植一棵，植了20 米，从头开始栽。五（1）班植了多少棵树？

活动二：五（2）班接着五（1）班继续每隔5 米栽一棵树，植了20 米。五（3）班接着五（2）班继续每隔5 米植一棵树，植了20 米，尽头安装路灯。五（2）班和五（3）班分别植了几棵树呢？

同样是20 米距离，通过画图学生发现（如图4），植的棵数却不一样。但学生三年级已有了“间隔排列”的知识结构基础，通过“一一对应”他们不难发现：五（1）班属于“两头都植”的情况，棵数=间隔数+1；五（2）班属于“ 一头植一头不植”的情况，棵数=间隔数；五（3）班属于“两头都不植”的情况，棵数=间隔数-1。