充液管路振动特性半解析建模及卡箍布局优化

2023-01-18张宇孙伟刘旭东

中南大学学报（自然科学版） 2022年11期

张宇，孙伟，刘旭东

(1.东北大学机械工程与自动化学院，辽宁沈阳，110819；2.东北大学航空动力装备振动及控制教育部重点实验室，辽宁沈阳，110819)

航空发动机管路系统主要用于传输燃油、滑油等工作介质，是保证航空发动机可靠工作的重要附件系统。航空发动机外管路主要通过卡箍固定在机匣上，发动机内部的转子或者气流激励会通过机匣传递到管路，当外激励的频率接近管路固有频率时，管路系统会发生共振，从而大幅度增加管路的振动幅度[1-2]。过大的振动会导致管接头裂纹、卡箍松动甚至断裂等故障，严重影响航空发动机工作的安全性及可靠性，因而，需要采用有效的减振措施来控制管路的振动。卡箍的支撑刚度及阻尼等力学参数会对管路系统的动力学特性产生直接影响，采用调整卡箍布局使管路避开发动机的激振频率被认为是一种最经济、最有效的管路系统减振方法。

为了获得最优的卡箍布局，需要执行管路系统的避振优化，而执行避振优化的前提是要创建一个合理的管路系统动力学分析模型。航空发动机中大部分管路处于充液状态，因而需要研究充液管路的动力学建模与分析方法。目前，以航空发动机管路为对象进行充液管路动力学的研究较少，但是以输油、输气和飞机液压管路等为对象的充液管路动力学已有大量研究，其建模方法包括传递矩阵法[3-4]、有限元法[5-6]、特征线法[7-8]、半解析法等。在这些建模方法中，半解析法由于所需自由度少、计算效率高得到了较为广泛的应用，如HUANG 等[9]根据Hamilton变分原理得到了输液管路的振动方程，并采用消元Galerkin法求解了特殊边界条件下输液管路的固有频率；初飞雪[10]根据Hamilton 原理推导了输液管路的振动变分方程，采用直接解法求解了两端简支管路的固有频率及临界流速；LIANG 等[11]以Euler-Bernoulli梁模拟管路，采用微分求积法及Laplace 变换分析了充液管路的振动特性；LI 等[12]使用He's 变分迭代法对输液管路进行了自由振动分析，得到了在不同边界条件下管路的临界流速和临界频率。现有的大部分管路系统半解析建模理论针对的是经典边界条件下的管路，对于多卡箍支撑的管路结构并不适用，因此需对其重新进行半解析建模。

以减振为目标，一些学者针对管路系统卡箍布局优化开展了研究，例如ZHANG等[13]以调节管路固有频率及动态响应最小化为优化目标，采用遗传算法求解得到了最优的卡箍位置。李鑫等[14]采用粒子群优化算法，以系统特征阻抗最小为目标函数进行了卡箍的布局优化，实现了充液管路的减振。GAO 等[15]以管路基频与激励频率差值最大及管路位移响应为优化目标，通过神经网络建立优化的代理模型并使用遗传算法进行求解，显著降低了管路系统的振动。刘伟等[16]以基频与激励频率差值最大化及随机振动的响应均方差最小化为目标，使用罚函数法对管路系统的卡箍位置进行了优化。柳强等[17]以管路的1阶和2阶固有频率为优化目标，使用Kriging 模型和NSGA-Ⅱ算法求解了最佳卡箍位置，大大提高了优化效率。TANG等[18]以卡箍位置为设计变量，以液压管路的累计疲劳损伤失效概率作为优化目标，采用序列二次规划法进行了求解，优化后显著提升了管路的动力学性能。总的来看，目前对于管路的卡箍位置优化以空管为主，虽然也有一些针对充液管路的卡箍位置优化，但是并没有明确液体参数对于充液管路卡箍布局优化结果的影响。

本文作者以多卡箍支撑充液管路为研究对象，采用半解析方法建立动力学模型，介绍建模的原理及流程。随后根据航空发动机的实际工作情况，建立以1阶固有频率最大为优化目标，以卡箍位置为设计变量的优化模型并采用粒子群算法进行优化求解。最后，通过与文献比对验证了所建立的半解析模型的正确性，进一步以三卡箍充液管路为实例实施了卡箍布局优化研究，并分析了液体质量、流速以及管径等对卡箍布局优化结果的影响。

1 多卡箍支承充液管路半解析建模

图1所示为含有N个卡箍支撑的充液管路，其中，l为管路总长度，D和d分别为管的外径和内径，v为管内液体流速。由于充液管路含有多个卡箍支撑，因此属于超静定结构，为了完成其半解析建模，将该系统分为空管、卡箍、管内流体3个部分，每一部分单独进行能量分析，最后再进行组合，最终推导出充液管路总的动力学方程。

图1 多卡箍支撑充液管路模型Fig.1 Liquid-filled pipeline model with multi-clamp support

1.1 能量分析

管路系统的横向位移w可表示为

式中：ω为管的振动频率；φ为相位；W(x)为系统的振型函数，可表达为

式中：ai为待定系数；Pi(x)为一系列特征多项式，可由Graham-Schmidt 正交化求得[19]，求解的基本过程如下：

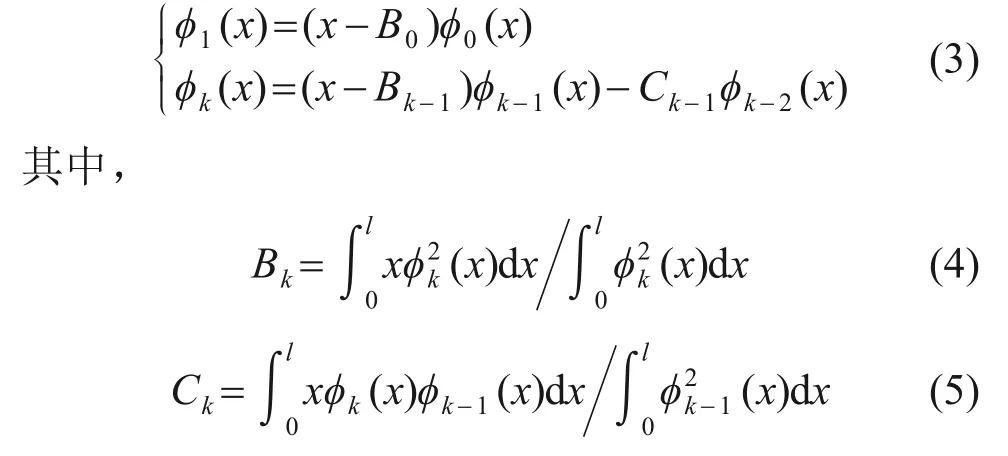
对ϕk(x)进行归一化处理可得：

特征多项式Pi(x)满足以下正交条件：

1.1.1 空管管体能量分析

由Euler-Bernoulli 梁理论，空管部分的势能Vp和动能Tp分别为

式中：EI为管的抗弯刚度；mp为管的单位长度质量。

在偏离平衡位置最远处，管路具有最大势能Vpmax，在静平衡位置具有最大动能Tpmax，其表达式分别为

1.1.2 卡箍能量分析

参照已有的卡箍动力学建模[20-21]，卡箍可以用弹簧-阻尼单元来进行模拟，并忽略阻尼效应，将1 个卡箍等效为2 对弹簧单元，每对弹簧单元由1个线性弹簧和1个扭转弹簧组成，卡箍部分的简化模型如图2所示，以管路的左端点为原点O，由原点向右为正方向，xk(k=1,2,…,2N)为第k对弹簧距原点O的距离，线性弹簧的支撑刚度为Kv，扭转弹簧的扭转刚度为Kθ，每个卡箍对应的弹簧刚度均相同。

图2 卡箍简化模型Fig.2 Simplified clamp model

位于xk处的弹簧对的势能为

1.1.3 流体介质能量分析

设管内的液体流动速度恒为v，流体的单位长度质量为mf，则管内流体的动能Tf和最大动能Tfmax分别为

将空管、卡箍、流体的最大势能和最大动能相加，得到多卡箍支撑充液管路的总势能Vmax和总动能Tmax分别为

1.2 动力学模型

将式(2)分别代入式(10)，(11)，(13)和(16)中可得：

针对式(19)～(22)，设空管的刚度Kpij及质量Mpij、第k对弹簧的刚度、流体的刚度Kfij及质量Mfij分别为

进一步，设I=Vpmax+Vgmax-Tpmax-Tfmax=Vmax-Tmax，利用拉格朗日方程

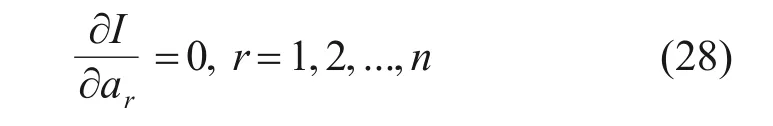
得到多卡箍支撑充液管路的动力学方程为

式中：K为刚度矩阵，K=Kp+Kg+Kf，Kp为空管管体的刚度矩阵，Kg为卡箍的刚度矩阵，Kf为流体的刚度矩阵；M为质量矩阵，M=Mp+Mf，Mp为管体的质量矩阵，Mp为流体的质量矩阵。

求解式(29)，可以得到多卡箍支撑充液管路的前n阶固有频率fr，其中，r=1，2，…，n。

2 多卡箍支承充液管路布局优化

为了进行多卡箍支撑充液管路卡箍的位置优化，首先需要建立合理的动力学优化模型，同时选择合适的算法对模型进行求解。

2.1 优化模型

大部分管路刚性较大，因而在管路系统设计时，选择管路系统1阶固有频率大于等于激振频率的1.25 倍[22]，保证管路系统所有固有频率避开激振频率。这里选择充液管路1阶固有频率f1最大为本文的优化目标。

设计变量示意图见图3，图中，Di为第i个卡箍左端面与管路最左端的距离，其中i=1，2，…，N。以卡箍在管路中的位置Di为设计变量，根据相关设计标准的内容[23]，两个卡箍之间存在最大距离的要求，卡箍不可能在管路上随意布置，图3中的虚线框区域为各个卡箍的允许布置区域，每个卡箍都有其移动的上下限，设Dli和Dui分别为第i个卡箍的移动下限及上限，即Dli≤Di≤Dui。

图3 设计变量示意图Fig.3 Schematic diagram of design variables

最终，建立的多卡箍支撑充液管路的卡箍布局优化模型为

需要说明的是，为了研究充液状态对卡箍布局优化结果的影响，在整个优化模型中，并未引入外界对管路的激振频率。

2.2 优化求解

采用粒子群优化(particle swarm optimization,PSO)[24-25]对上述优化模型进行求解。粒子群优化算法中粒子、位置、速度、适应度、个体最优值、全局最优值等术语与本研究中卡箍布局优化模型之间的对应关系见表1。

表1 粒子群优化中的术语与卡箍布局优化的对应关系Table 1 Relationship between terms in PSO and clamp layout optimization

本研究的优化目标为多卡箍支撑充液管路的1阶固有频率最大，是单目标优化，根据粒子群算法的基本思想，充液管路卡箍布局优化的算法流程如下。

1) 初始化粒子。选择Z组粒子，赋予每个粒子随机的初始卡箍位置，组成初始的卡箍位置点集合，并赋予初始速度。

2) 计算适应度。根据给出的每组初始卡箍位置点信息(即一个粒子)分别计算其对应的充液管路的1阶固有频率。

3) 计算个体最优值。对每组卡箍位置点，将其当前得到的1阶固有频率与其先前迭代过程得到的个体最优值进行比较，若当前的1阶固有频率更大，则用当前的1阶固有频率取代其先前的个体最优值，成为新的个体最优值。

4) 计算全局最优值。对全部卡箍位置点(所有Z组粒子)，将当前得到的1阶固有频率与先前得到的全局最优值进行比较，若当前的1阶固有频率更大，则用当前的1 阶固有频率取代其全局最优值，成为新的全局最优值。

5) 更新粒子速度和位置。按照算法的迭代规则，由新的个体最优值和全局最优值得到新的卡箍位置点集合的位置及速度信息，准备进行下一次的迭代计算。

6) 判断是否满足中止条件。若满足则输出当前的全局最优值作为优化得到的最优值，并记录其对应的卡箍位置点；若不满足，则返回步骤2)，开始新一轮的计算。

3 实例研究

以三卡箍支撑充液直管为例，对其进行半解析建模以及实施充液管路卡箍布局优化，充液直管的管长l=500 mm，外径D=8 mm，内径d=6.4 mm，弹性模量E=1.99×1011Pa，管材密度ρp=7 850 kg/m3，泊松比μ=0.3，管内液体密度ρf=1 000 kg/m3，用于模拟卡箍的线性弹簧的刚度Kv=4.3×105N/m，扭转弹簧的刚度Kθ=80 N·m/rad，3个卡箍的刚度相同，卡箍的宽度为14 mm。

3.1 模型正确性校验

文献[5]使用有限元法求解管路的固有特性，以文献[5]中的充液悬臂管为对象验证所建立的半解析模型的准确性，悬臂管模型[5]如图4所示，悬臂管长度l为1 010 mm，外径D为22.85 mm，内径d为19.65 mm，管材密度为2 800 kg/m3，弹性模量为70 GPa，泊松比为0.3，管内液体密度为1 000 kg/m3。当管内液体速度v=10 m/s时，充液悬臂管的前4阶固有频率如表2所示。

图4 充液悬臂管模型[5]Fig.4 Liquid-filled cantilever pipeline model[5]

表2 充液悬臂管各阶固有频率Table 2 Natural frequencies of liquid-filled cantilever pipe

由表2可以看出，采用有限元法得到的该充液悬臂管模型的前4阶固有频率与本文采用半解析法建模得到的前4阶固有频率差别较小，证明了本文采用半解析法建模求解充液管路固有频率的准确性。

3.2 振动特性分析

三卡箍支撑充液直管模型如图5 所示，3 个卡箍在管路上的初始位置分别为D1=75 mm，D2=250 mm 和D3=425 mm，管内液体以速度v匀速流动。

图5 三卡箍支撑充液管路Fig.5 Three-clamp support liquid filling pipeline

在考虑流体作用时，设置流速分别为0，2，5和10 m/s 的工况。在不同流速下空管及充液直管前3阶固有频率如表3所示。

表3 空管及充液管路固有频率对比Table 3 Comparison of natural frequencies of empty pipe and liquid-filled pipe

由表3可以看出，由于液体质量的影响，充液管路的各阶固有频率相比空管的下降较大；随着流速增大，在考虑的速度范围内，各充液管路的各阶固有频率变化较小。可见，在低流速下状态下计算充液管路的固有频率时，可忽略液体流速的影响，只需要考虑液体质量的影响，将液体质量视为管路的附加质量进行计算。

3.3 优化求解

以三卡箍支撑充液管路的1阶固有频率f1最大为优化目标，采用粒子群优化算法对充液管路的卡箍位置进行优化，设置粒子群算法中的各项参数如下：粒子数Z=50、最大迭代次数T=100，各个卡箍的允许布置范围为Dl1=2 mm、Du1=150 mm、Dl2=170 mm、Du2=316 mm、Dl3=336 mm、Du3=484 mm。先针对空管，验证优化算法的有效性，设优化前的卡箍位置为D1=75 mm，D2=250 mm 和D3=425 mm，计算其1阶固有频率，再使用粒子群优化算法对该空管模型进行卡箍位置优化，优化结果如表4所示。

表4 空管优化前后结果对比Table 4 Comparison of results before and after optimization for empty pipeline

由表4可以看出，采用粒子群优化算法对管路卡箍位置进行优化后，管路的1阶固有频率提升了约68 Hz，验证了所采用的粒子群优化算法的有效性。

优化过程中1阶固有频率的变化及优化进程如图6 所示。从图6 可以看出，当计算到第10 代时，结果开始收敛并得到最优值。

图6 1阶固有频率优化迭代过程Fig.6 Optimize iterative process of the first-order natural frequency

3.3.1 充液对优化结果的影响

将空管的优化结果与流速为2 m/s 状态下充液管路的优化结果进行对比，2组管路优化前的卡箍位置均为D1=75 mm，D2=250 mm 和D3=425 mm，管路优化结果如表5所示。

表5 空管及充液管路的优化结果Table 5 Optimization results of pipeline under condition of empty and liquid filled

由表3 和表5 可知，充液管路优化后的1 阶固有频率提升了约63 Hz，与表4 对比可知，空管和充液管路的优化效果相差不大。与振动分析结果相似，充液管路系统卡箍位置优化的目标函数值也显著减小。但是对于设计变量最优值来说，空管及充液管路的最佳卡箍位置是相同的，说明充液与否对卡箍布局优化结果没有影响。

3.3.2 流速对优化结果的影响

为了研究管内流体速度变化对于优化结果的影响，设置流速分别为0，2，5和10 m/s，不同流速工况下优化后的管路系统的1阶固有频率及最佳卡箍位置如表6所示。

表6 不同流速下充液管路的优化结果Table 6 Optimization results of pipeline filled liquid at different flow rates

由表6可以看出，当管内流体速度增大时，管路系统优化后的目标函数值略微减小，这与3.2节振动分析的结果是一致的。但是，各个流速状态下优化后的设计变量最优值是相同的，也即卡箍布局优化结果相同。综上可认为管内流体速度对充液管路卡箍位置优化的目标函数值略有影响，在低速状态下，可认为目标函数值基本不变，而对卡箍布局最优值完全没有影响。

3.3.3 管径对优化结果的影响

为了分析管径对优化结果的影响，设置管径分别为8，10，12，14和16 mm的直管，其余参数均相同，5 组管路均在流速2 m/s 下进行卡箍位置优化，优化结果如表7所示。

表7 不同管径管路的优化结果Table 7 Optimization results of pipeline with different pipe diameters

由表7可以看出，优化后的目标函数值随着管径的增大而增大，这主要是因为管型的变化导致的，但是各个管径的设计变量最优值基本相同，仅相差约1 mm，考虑到实际管路安装中的误差，偏差可以忽略不计。

综合以上结果分析可知：1) 若仅以最大1阶固有频率为优化目标，则可以不考虑管路中的液体，仅以空管动力学模型为基础模型进行优化，不影响卡箍布局优化结果；2) 若要考虑管路的1阶固有频率远离激振频率的程度，则必须以充液管路为基础模型进行卡箍布局优化；3) 在进行充液管路的卡箍布局优化时，在低速状态下，可以不考虑流速的影响，而仅将液体视为附加质量；4) 对于管型相同仅管径不同的管路，若仅以最大1阶固有频率为优化目标，则可以忽略管径的影响。