基于球压痕法的玻璃材料强度原位快速表征技术
2023-01-18刘小根齐爽万德田孙与康包亦望郑德志
刘小根 ,齐爽,万德田 ,孙与康,包亦望,郑德志
(1.中国建筑材料科学研究总院有限公司 绿色建筑材料国家重点实验室,北京,100024;2.中国国检测试控股集团股份有限公司,北京,100024)
作为材料基因组技术的三大要素之一,材料高通量实验技术近年来备受关注,其宗旨是在短时间内完成大量样品的制备与表征,一次可检测多个样品或对同一样品进行多种性能检测,以实现加快材料的研发与应用进程[1]。玻璃材料是国民经济建设的重要基础材料,被广泛应用于建筑、汽车、家电等行业。随着功能化需求的不断发展,玻璃材料已由原先的透光单一功能材料不断地向“结构-功能”一体化应用方向发展,因此,其强度是表征其抗损毁性能的重要指标之一。在玻璃结构工程设计中,获取玻璃材料的强度对指导玻璃材料结构设计与应用有着举足轻重作用。
高通量玻璃材料合成后,如需了解玻璃材料的成分及其不均匀性、残余应力和缺陷等对其强度的影响,一般需要根据特定的标准制备样品进行逐一测试,由于测试本身具有破坏性,且需做成标准样品进行测试,无法原位快速表征玻璃材料的强度。因此,开发合理的玻璃材料局部强度的无损或微损、原位快速表征技术,是实现其高通量测试的前提,对加快研发高性能玻璃材料、提升材料质量具有重要的理论和实际意义。
压痕试验是测定玻璃、陶瓷材料及金属、高聚物力学特性的一种十分有效且简便的方法。球压试验是在赫兹接触理论基础上发展起来的一种材料局部力学性能测试方法,在球压入过程中,材料受到球压头的压力,历经弹性变形、塑性变形以及弹性释放等过程,因此能够反映材料的许多基本力学性能[2-3]。球压试验因“无样”、“微损”地实现材料的力学性能测试,可解决传统试验方法和小尺寸试样试验方法的测试难题[4]。WARREN等[5-6]采用球压技术进行了玻璃和陶瓷的表面残余应力测试,证明了该技术可为工程玻璃及陶瓷的质量和过程控制提供技术支持。BAO等[7-8]基于球压开裂时的最大压痕应力随压球半径的增大而减小,且远高于常规强度这一特征,采用均强度理论分析了球压附近的应力分布,获得了球压作用下材料局部强度的计算公式。在此基础上,PETIT等[9]对钢化玻璃表面残余应力及断裂韧性进行了测试和比较,分析了其误差。KEISUKE 等[10-11]进行了微光弹性测量,获得了石英和钠钙玻璃的球压附近三维应力图,解释了球压作用下这2种不同玻璃的破坏模式。谈至明等[12]认为,进行有限厚度、大压入的材料力学球压试验时,材料试样厚度与球压接触半径之比应大于6。对材料性能的高通量定量表征,关键在于测试方法及装置的研发[13-14]。在材料力学性能表征方面,DAO 等[15]利用纳米压痕技术实现了梯度材料或者微区材料的纳米硬度和弹性模量测试,KIM 等[16]借助量纲分析和数值仿真反演了材料的真实应力-应变关系,通过微悬臂梁试验获得微区材料的断裂韧性。系列压痕法力学性能测试装置[17-18]的研发有力地促进了材料高通量测试技术发展。
本文作者基于球压痕及均强度理论推导玻璃局部强度与初始环形裂纹直径之间的关系式,提出通过测量初始环形裂纹直径来获得玻璃强度及残余应力,从而为玻璃材料强度原位快速表征提供一种新的技术途径。
1 球压技术测试玻璃材料强度基本理论
对于球与玻璃材料表面接触,若球压痕半径与玻璃厚度之比足够小,则可把玻璃材料视为无限大体。设在压力P的作用下,半径为R的球与玻璃的接触区域为圆形,其半径为a。当压力P逐渐增大时,则可在接触区域外围附近形成环形裂纹并向纵深扩展,如图1 所示,图中,Em和vm分别为玻璃材料的弹性模量和泊松比;Ei和vi分别为球压头的弹性模量和泊松比。图2所示为环形裂纹俯视和侧视照片。在柱状坐标系下,应力分布状态如图3 所示。根据赫兹(HERTZHR)接触理论,球压接触区域附近玻璃内部的应力计算如下[11,19]:
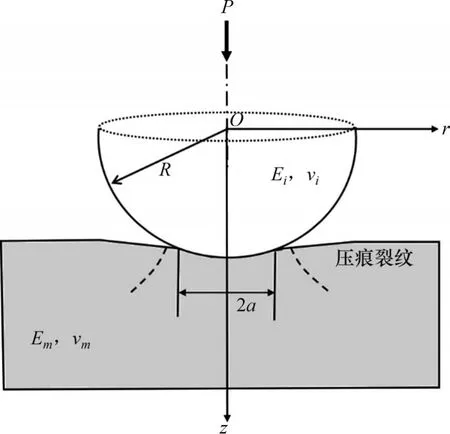
图1 球压技术测试示意图Fig.1 Schematic of spherical indentation test method

图2 球压测试压痕形貌照片Fig.2 Indentation morphology by spherical indentation test

图3 柱状坐标系下应力分布状态示意图Fig.3 Schematic of stress distribution in cylindrical coordinate system
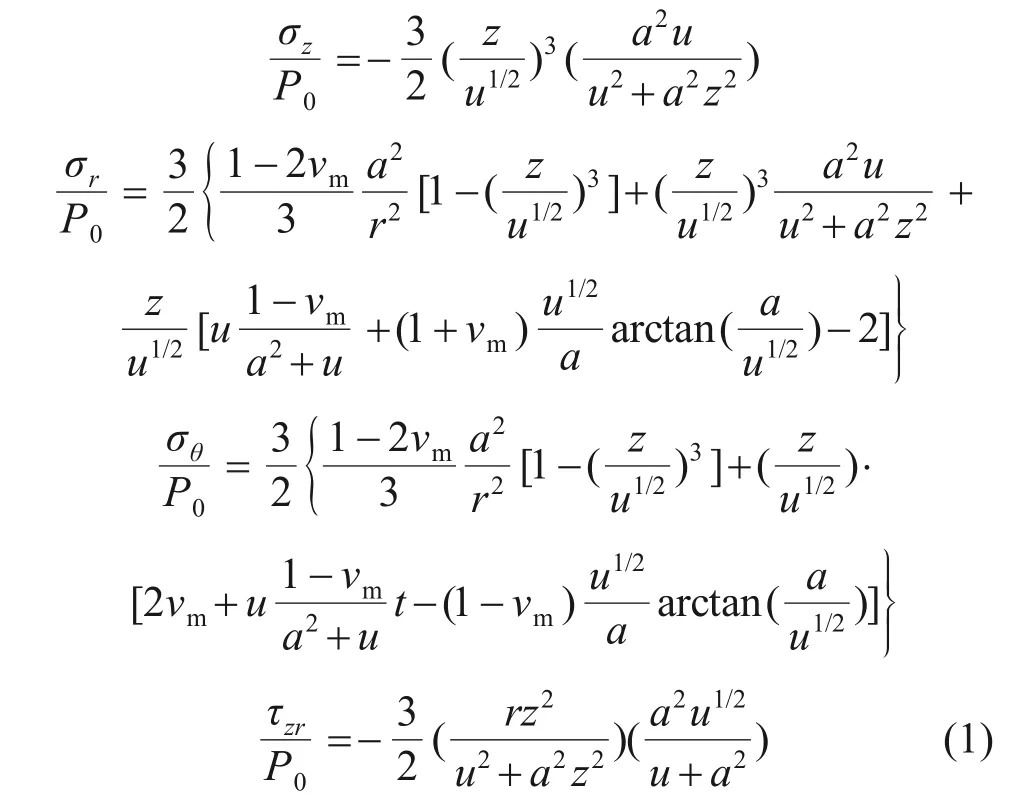
式中:σz,σr和σθ分别为球坐标z,r,θ方向的应力;τzr为剪应力;P0为平均接触压力,P0=P/(πa2);u为接触区域表面垂直变形,u=z2-a2+

其中:E*为等效弹性模量。
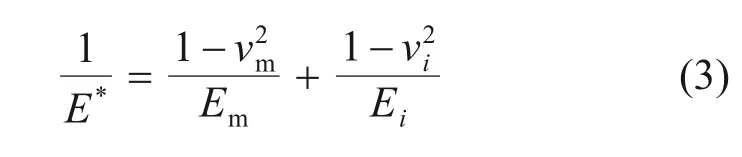
根据赫兹接触理论,最大拉应力σmax发生在玻璃表面接触圆的边缘(z=0,r=a)处[19]:
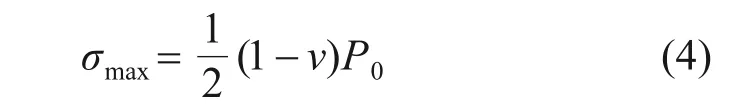
BAO等[8]通过试验发现,脆性材料的接触表面产生环形裂纹时,按式(4)计算得到的最大拉应力总是比材料的实测强度高得多,他们认为这是球压接触圆周边附近玻璃内部的拉应力存在较大的应力梯度,而脆性材料破坏存在应力梯度效应所致。基于此现象,BAO等[8]提出了均强度理论,认为脆性材料破坏不是在最大拉应力处,而是在最大平均拉应力处,并采用数值计算获得了玻璃径向应力与平均应力分布关系,玻璃材料在破坏发生区深度Δ=0.03 mm 时,离接触圆中心1.15a处的平均应力最大,且环形裂纹在此处开裂(即环形裂纹半径A=1.15a)。最大平均应力(局部强度)σloc计算公式为:
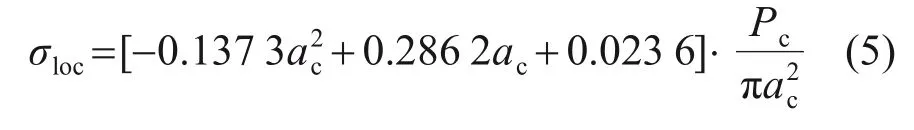
式中,Pc和ac分别为开裂时的临界载荷和临界球压接触半径。
采用式(5)计算玻璃材料的局部强度时,必须准确获得球压玻璃开裂时刻对应的载荷及接触半径,但对于球压微小损伤,即使采用高灵敏声发射技术也难以监控玻璃起裂时刻,从而难以准确获得对应的载荷及接触半径,因此,本文直接采用球压压痕直径来反演玻璃材料的局部强度及残余应力,并设计了相关实验装置以实现玻璃材料局部强度及残余应力原位快速表征。
2 试验方法
2.1 试验材料
试验压头为直径5 mm的碳化钨圆球,采用不同厂家生产的普通钠钙玻璃及物理钢化玻璃(表面应力标定值为110 MPa)进行普通球压试验,包括含打孔的表面应力不均的钢化玻璃(厚度为6 mm,长×宽为300 mm×300 mm) 1 片和普通玻璃样片(厚度为5 mm,长×宽为10 mm×10 mm) 16片。
2.2 实验设备及参数
加载设备为MTS-C45-105 微机控制电子万能试验机,载荷精确度为0.1 N,压痕观测设备为KEYENCE VHX-970F 超景深三维显微系统,放大倍数为5~200,尺寸测量系统精确度为1.0 μm。
将仿真模型中电感值分别取为1 mH和20 mH,其余参数固定,根据仿真结果可知增大电感L取值,直流电压的振荡幅值变大,电池电流和直流电压振荡的周期减小,系统稳定性变差;当电感L取值较小时直流电压振荡幅值变小,电池电流的振荡更加剧烈。
2.3 实验过程
为避免不同加载速率对强度影响,选择GB/T 37781—2019 中规定的位移等速加载速率(5 mm/min)进行加载,实验过程中,观察是否产生环形裂纹,并记录环形裂纹产生的载荷及其形貌。
3 结果与讨论
3.1 球压作用下环形裂纹的形成与扩展特征
采用普通钠钙玻璃和钢化玻璃进行普通球压试验,逐步增大加载载荷(每级增加5 N),采用显微镜观察压入表面是否存在环形裂纹,以此确定玻璃产生环形裂纹对应时刻的临界载荷(Pc);确定临界载荷后,继续递增加载载荷(每级增加临界载荷的5%),并观测压痕形貌及直径变化。
图4和图5所示分别为普通玻璃和钢化玻璃在不同载荷作用下的压痕裂纹形貌。由图4和图5可以看出,在临界载荷作用时,球压附近玻璃表面会形成一明显初始环形裂纹(图4(a)和图5(a));继续递增加载载荷,初始环形裂纹的直径并不会随之改变,而是趋于稳定,但裂纹会向厚度纵深方向扩展,并形成喇叭状(图4(b)和图5(b))。继续递增加载载荷直到初始环形裂纹的圆环内玻璃破碎开裂,此时,初始环形裂纹表观被掩盖,并形成可见次环形裂纹,次环形裂纹的直径小于初始环形裂纹的直径,并随压入载荷增大不断减小(图4(c)和图5(c))。

图4 不同压入载荷作用下普通玻璃压痕形貌照片Fig.4 Indentation morphology of common glass under various indentation loads

图5 不同压入载荷作用下钢化玻璃压痕形貌照片Fig.5 Indentation morphology of tempered glass under various indentation loads
初始环形裂纹形貌与受载处玻璃局部强度有关,通过逐步递增载荷获得不同载荷下玻璃的环形裂纹直径变化结果如图6所示。可见,无论普通玻璃还是钢化玻璃,只有当加载载荷增大至临界载荷的120%以上时,次环形裂纹才会形成,其直径也缩小,在此之前,初始环形裂纹直径趋于稳定值。次环形裂纹直径缩小主要是球压作用下玻璃受压剪作用破坏并持续扩大导致的。
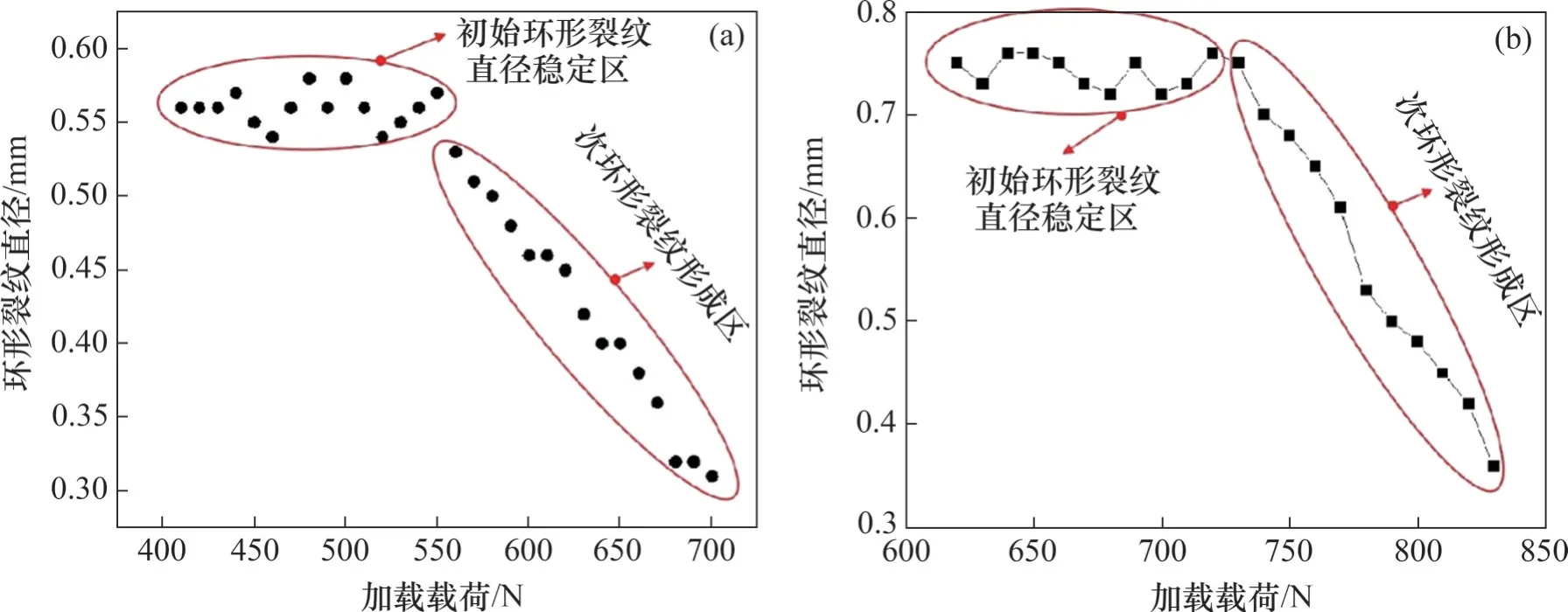
图6 压入载荷与环形裂纹直径关系曲线Fig.6 Relationship between pressure loads and diameters of indentation crack
3.2 基于初始环形裂纹直径的玻璃局部强度及残余应力测量
由3.1节分析可知,初始环形裂纹直径稳定值对应了一个较大的加载载荷区间,实际测试时,只要在这一区间选择一个加载载荷,即可获得初始环形裂纹直径,若能建立初始裂纹直径与其对应位置强度关系,则可通过测量初始裂纹直径反演压入部位处的玻璃强度。
根据式(2)可得:

式中,Ac为所测初始环形裂纹的半径,Ac=1.15ac。
将式(6)代入式(5)进行修正可得:
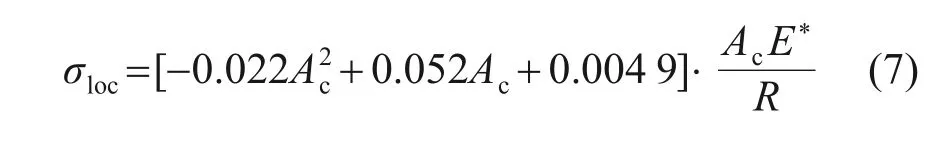
在玻璃及球头材料参数确定的条件下,E*可根据式(3)确定,并也为定值。试验玻璃材料及球头材料参数及E*见表1。
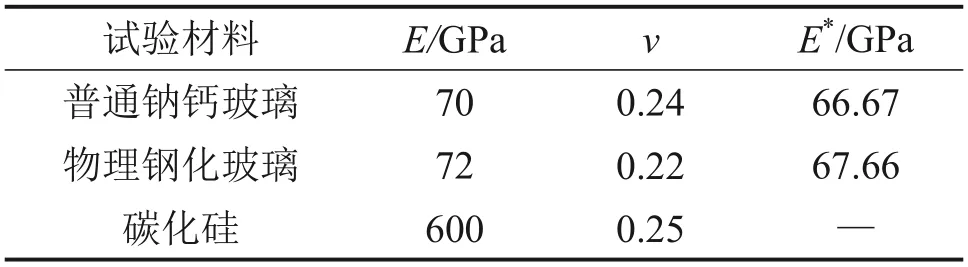
表1 试验材料及参数[9]Table 1 Experimental materials and calculating parameters[9]
由式(7)可知,只需在环形裂纹稳定区内选择任一加载载荷(加载载荷范围通过初步试验确定),即可获得初始环形裂纹直径Ac,从而得到该处的局部强度。
采用本文球压法对普通钠钙玻璃和钢化玻璃的局部强度进行测试,并与按GB/T 37781—2019[20]中的三点弯曲强度试验方法测得的强度进行比较。球压法与三点弯曲法测试的玻璃强度对比如表2所示。从表2可见:采用球压法测量得到的玻璃局部强度比采用GB/T 37781—2019 方法测得的强度大,这主要是因为球压法所测部位影响区域微小,其强度代表微区强度,因此,其值会比采用常规方法测得的强度更高。钢化玻璃的残余应力为其局部强度与普通玻璃的局部强度之差[8]。由表2 可知,球压法测得的钢化玻璃残余应力与其标定值较接近。
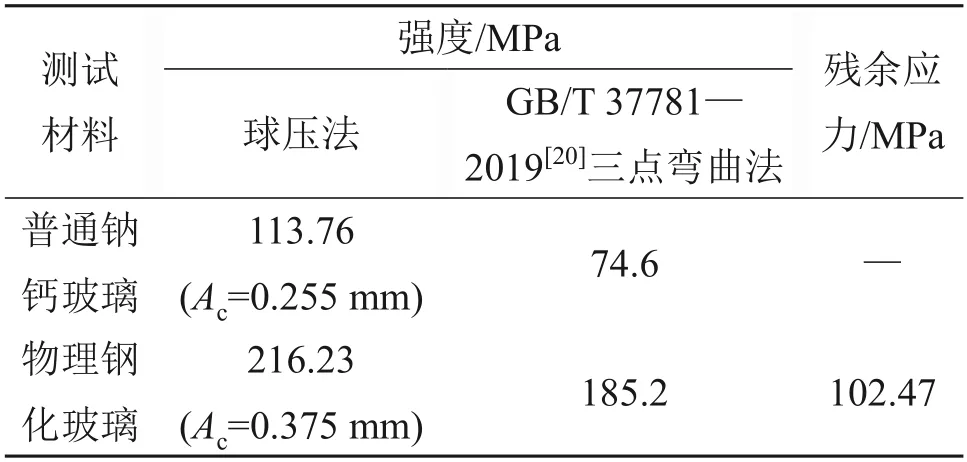
表2 球压法与三点弯曲法测试的玻璃强度对比Table 2 Comparison of glass strength tested by spherical indentation method and three-point bending method
3.3 基于球压痕技术的玻璃材料强度原位快速表征
3.3.1 测试装置设计
为实现基于球压痕技术的微损、原位、快速表征玻璃材料或构件的表面强度,设计一套测试装置,其示意图如图7 所示。该装置包含4 个部分:

图7 基于球压技术的玻璃材料强度原位快速表征装置示意图Fig.7 Schematic of in-situ and fast characterization for glass materials strength by spherical indentation method
1) 试验加载模块(试验机),用于对玻璃材料表面进行球压加载,载荷精度应满足试验要求,且加载速率可调。
2) 图像获取模块,用于拍摄并保存球压压痕照片,需采用放大倍数不低于50 倍的高精度光学放大镜。
3) 运动模块,用于对样品进行传送和移位。运动模块需在X、Y方向均可移动。通过调节运动模块,可实现在同一试样任一位置或不同试样不同位置进行连续加载。运动模块X、Y方向调节精度应达到0.1 mm并定位。
4) 图像处理及分析模块,用于对获取的压痕图像进行自动分析和处理,除能精确获得环形裂纹直径外,还能识别环形裂纹是否为初始环形裂纹或次环形裂纹。计算机能够根据获取的图像自动计算材料的强度。
3.3.2 试验验证
采用本文设计的装置进行一次性多点加载试验,获得物理钢化玻璃不同部位的局部强度和残余应力及普通钠钙玻璃的球压强度。物理钢化玻璃加载载荷为700 N,测点16个,测点位置示意图见图8(a)所示;每片普通钠钙玻璃的测点为1 个,加载载荷为500 N,16片普通钠钙玻璃的测点位置示意图如图8(b)所示。试验过程中,每个测点从加载→压痕拍照→压痕直径测量→测点强度计算所耗费的时间约为1 min。测试均在玻璃表面获得了符合要求的初始环形裂纹,其中,物理钢化玻璃测点1~16 的环形裂纹形貌如图9 所示,其强度及残余应力见表3。普通钠钙玻璃各测点的压痕形貌见图10,其强度见表4。测试结果显示,物理钢化玻璃表面强度离散性较大,这与测点的分布位置及钢化应力不均有关,特别是在打孔附近,局部强度明显低于其他部位的强度,与文献[21]的分析结果较吻合,普通钠钙玻璃测试结果显示各厂家生产玻璃的强度比较接近。
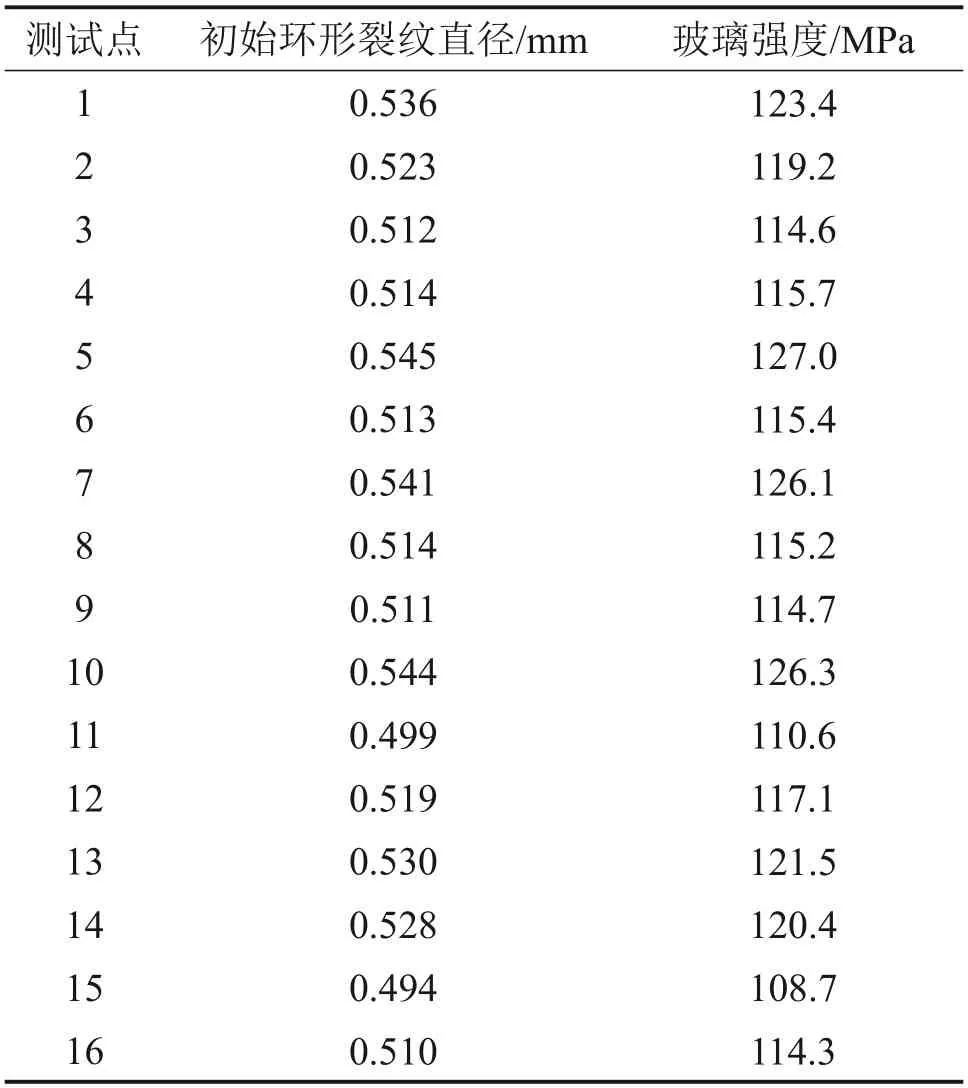
表4 普通钠钙玻璃各测点强度Table 4 Strength of common glass at various indentation points
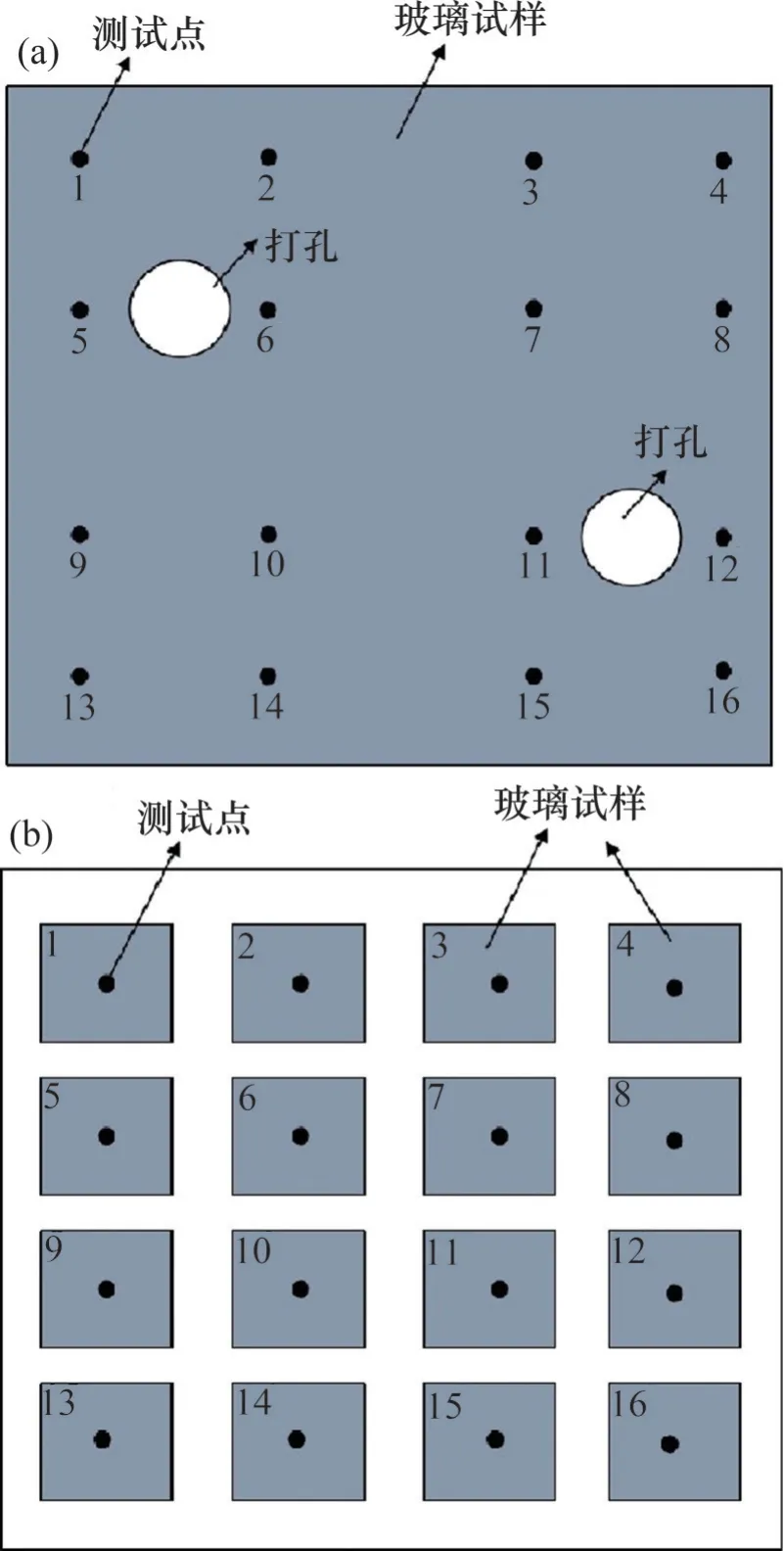
图8 原位快速表征技术测点位置示意图Fig.8 Schematic of test points location for in-situ and fast characterization
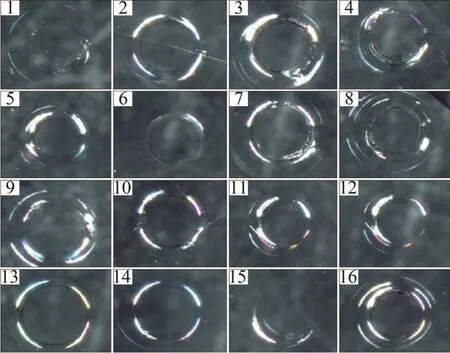
图9 物理钢化玻璃各测点环形裂纹形貌Fig.9 Indentation morphology of physically tempered glass at various indentation points
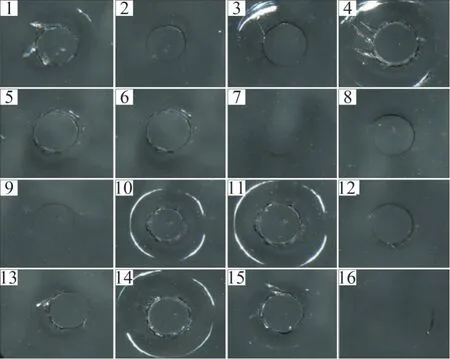
图10 普通钠钙玻璃各测点环形裂纹形貌Fig.10 Indentation morphology of common glass at various indentation points
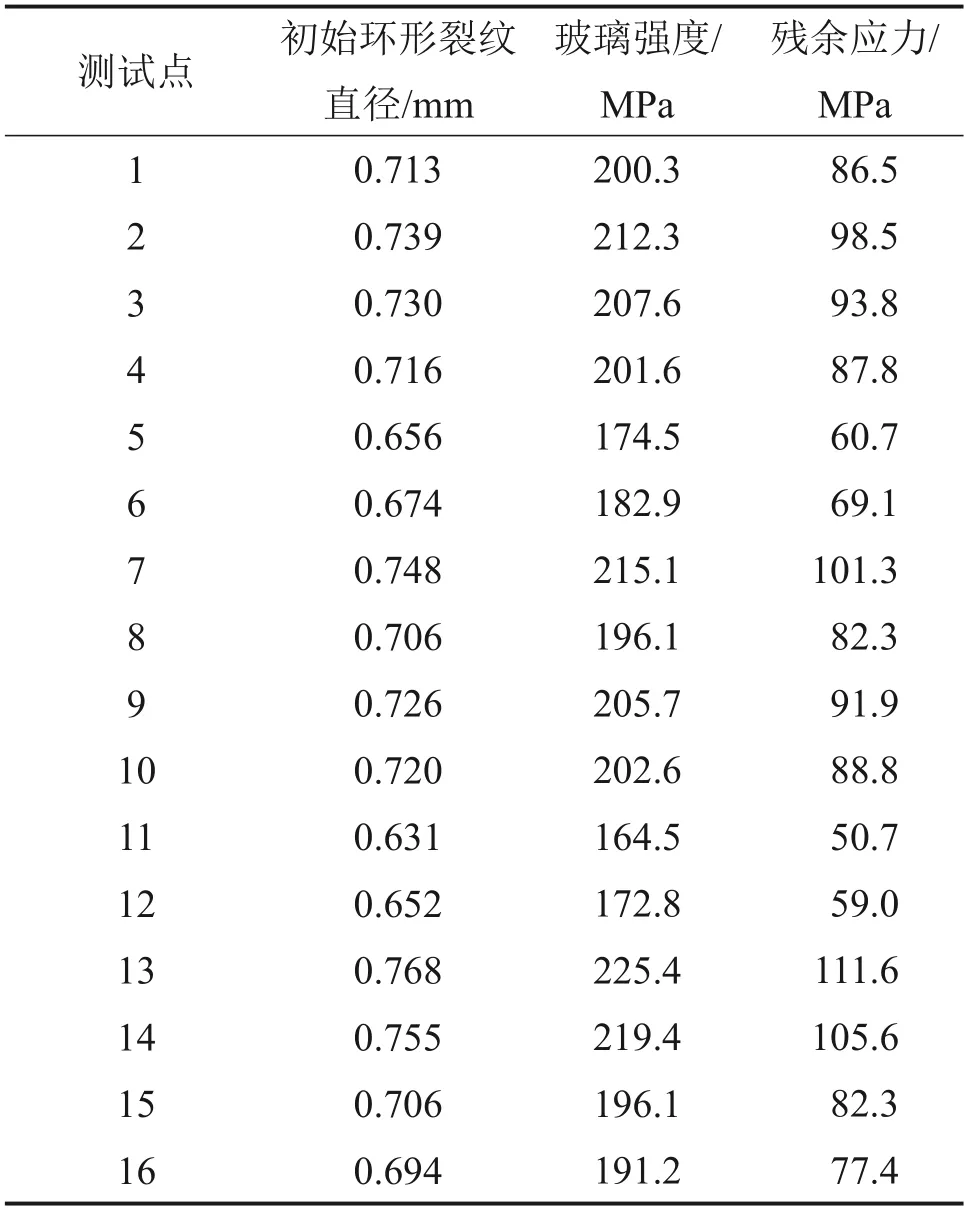
表3 物理钢化玻璃各测点强度及残余应力Table 3 Strength and residual stress of physically tempered glass at various indentation points
4 结论
1) 采用球压试验获得的玻璃表面初始环形裂纹直径存在一个不随压力变化的稳定区,只有当加载载荷递增至临界载荷的120%以上时,初始环形裂纹的圆环内部玻璃才会受压剪破碎开裂,并形成次环形裂纹,次环形裂纹直径随加载载荷增大而减小。
2) 初始环形裂纹直径与玻璃开裂时的强度相关。基于均强度理论获得了玻璃局部强度与初始环形裂纹直径之间的关系式。采用均强度理论修正式能够根据初始环形裂纹直径较准确地反演玻璃材料的局部强度及残余应力。
3) 基于球压痕法可进行玻璃材料成分及不均匀性、残余应力、缺陷等对其强度影响的原位快速表征分析。如能建立压痕形貌与其他材料力学性能如断裂韧性、硬度的相关性,还可实现通过一次压痕试验进行多种力学性能高通量表征测试。后续应对测试方法的适用范围、误差来源及设备改进进行更深入的研究。
