盾构隧道管片螺栓连接纵缝压弯承载力解析

2023-01-18王海峰高晓静李鹏飞贾子琦

北京交通大学学报 2022年6期

王海峰，高晓静，李鹏飞，贾子琦

（1.南通铁建建设构件有限公司，江苏南通 226000；2.北京工业大学城市安全与灾害工程教育部重点实验室，北京市 100124）

盾构法隧道衬砌结构是由若干弧形管片通过螺栓连接而成的预制拼装结构，目前的工程实践与相关研究表明：管片接缝是盾构隧道衬砌结构的薄弱环节，接头的受力特性直接决定了隧道结构的承载能力与安全性能［1-6］.根据管片纵向接缝的几何构造、接缝内外侧的嵌缝，可将纵缝接缝面分为外缘混凝土、核心混凝土、螺栓、内缘混凝土［7］.

目前，盾构管片接头的力学性能一般通过管片接头相关的试验、解析推导和数值模拟进行研究.张厚美等［8-10］通过管片接缝试验，研究了管片接缝的受力、变形及破坏过程，分析了各影响因素对接缝强度和刚度的影响，建立了管片接头抗弯刚度的经验公式，并进行了相应的三维有限元分析.闫志国等［11］基于某输水隧道工程，进行了管片接头原型荷载试验研究，明确了管片接缝刚度具有一定的阶段性，并为管片接头关键力学参数给定了相关取值范围.朱合华等［12］基于管片接缝试验的结果和理论分析，归纳了适用于描述接缝转动刚度的线性、双线性和非线性模型.Li等［13-14］采用盾构隧道原型管片接头试验和数值模拟的方法，研究了不同轴力水平下接头的变形性能.庄晓莹等［15］分别采用弹塑性本构和弹塑性损伤本构，建立盾构管片接头三维有限元模型，模拟正负弯矩下接头压弯破坏全过程，并依据模拟结果给出了接头健康评价指标.Liu等［16-18］依托于整环试验研究结论，以盾构隧道管片纵缝为研究对象，对不同运营工况下管片接缝的承载性能进行了足尺试验研究，研究了结构破坏机理和承载性能，推导了纵缝的受力模型.Jin等［19］针对某复杂输水隧道接头断面，采用原型试验和有限元模拟的方法，研究了正负弯矩荷载下接头的变形和接头抗弯刚度.Feng等［20］进行了足尺的管片接头试验，并建立了相应的三维有限元模型，分析了管片接头破坏的发展过程，其模拟结果与试验结果具有较好的对应关系，但数值模型中螺栓采用的梁单元进行模拟，且未考虑螺栓与管片混凝土之间的接触.上述已开展的研究中的理论分析多为管片的接头刚度的研究，集中于对管片接头承载过程中某一特定状态的分析，对于接缝受力全过程、管片的极限承载能力以及管片接头在不同受力阶段的力学状态关注较少.

本文以盾构隧道管片纵缝为研究对象，针对当前运营地铁盾构隧道常规管片结构，建立了管片纵缝受力性能的解析模型，描述了盾构隧道管片纵缝承压全过程的力学特性，分析了管片纵缝的受力性能和破坏机理，可为盾构管片接头设计和接头病害预判及处理提供理论依据.

1 管片纵缝受力全过程理论分析

1.1 基本假定

在对接头受力全过程的分析过程中，需要对截面模型进行简化，并做出5个基本假定.

1）采用直接头型式来代替真实管片的弧形接头，并假定接缝断面在受力过程中始终保持为平面，接缝处的变形主要是由螺栓的变形、接缝面混凝土的压缩变形引起的，为简化理论推导，将混凝土及螺栓简化为弹性体，接缝转角θ定义为

式中：δ1、δ2分别表示接缝内、外侧张开量；H为接缝面高度.

2）假定管片接缝防水垫、定位孔及定位棒对接缝抗弯刚度无贡献.

3）管片接头的变形直接影响隧道结构的变形特性，且作为地下结构隧道的允许变形量较小，正常使用隧道管片接头大多处于弹性阶段，因此为简化理论推导过程，假设管片接头的混凝土及螺栓均为线弹性体，为确定接头的极限抗弯刚度，认为当混凝土压应力超过其极限抗压强度时混凝土压碎.

4）根据钢筋混凝土结构受力特性，管片接头在核心混凝土全截面受压阶段的截面压应力分布呈线性，在接头具有张开角后，压区混凝土表现出较强的非线性，假设此时压区混凝土的压应力分布图为标准的二次抛物线，且抛物线的顶点在受压区边缘.考虑到解析解的连贯性，假设核心混凝土全截面受压阶段截面的压应力呈矩形+抛物线形分布.

5）为简化相关计算，接头受压区边缘混凝土的压缩变形量δc为［21-22］

式中：σc为接头受压区边缘混凝土的压应力；E为混凝土的变形模量；l为压缩应变的影响深度，取为受压区高度.

1.2 接缝截面受力全过程理论解析模型

以正弯矩为例，将纵向接缝受力状态分为4个阶段：核心混凝土全截面受压阶段、螺栓以下部分核心混凝土受压阶段、螺栓以上部分核心混凝土受压阶段、外缘混凝土与核心混凝土共同承压阶段.通过对纵向接缝受力状态的划分以及各阶段的力学分析，建立其全过程力学模型.

1.2.1 核心混凝土全截面受压阶段

在核心混凝土全截面受压阶段，混凝土受压区高度y等于核心混凝土高度h，且螺栓不受力，即Tb=0.核心混凝土处于弹性阶段，在轴力N及弯矩M作用下其应力分布图如图1所示.

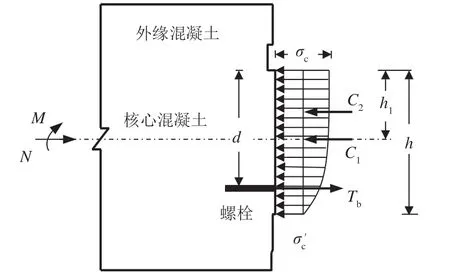
图1 核心混凝土全截面受压阶段模型计算简图Fig.1 Calculation schematic diagram at the compression stage of the full-section core concrete

根据受力图建立相应的力学平衡为

根据假设，将受压区混凝土压应力划分为矩形及抛物线形分布，并分别用C1、C2来代表各部分应力合力，故有

式中：σc、σc′分别为核心混凝土受压区上边缘及下边缘的压应力；b为管片厚度；d为密封衬垫嵌缝下边缘到螺栓的距离；h1为管片中性轴到密封衬垫嵌缝下边缘距离.

当给定接缝面所受轴力及弯矩，根据式（7）、式（8）即可求解出核心混凝土全截面受压阶段接缝处的受力状态.且根据假设，核心混凝土全截面受压阶段应满足σc′≥0，即可知核心混凝土全截面受压阶段的判定条件为

1.2.2 螺栓以下部分核心混凝土受压阶段

随着外荷载进一步增大，接缝的受力状态由核心混凝土全截面受压阶段逐渐过渡到螺栓以下部分核心混凝土受压阶段，此时接头具有一定的张开角，压区混凝土表现出较大的非线性，受力分析如图2所示，此阶段混凝土受压区高度范围为d≤y＜h，且螺栓仍不受力，即Tb=0.

图2 螺栓以下部分核心混凝土受压阶段计算简图Fig.2 Calculation schematic diagram at the compression stage of the partial core concrete below bolts

根据受力图建立相应的力学平衡为

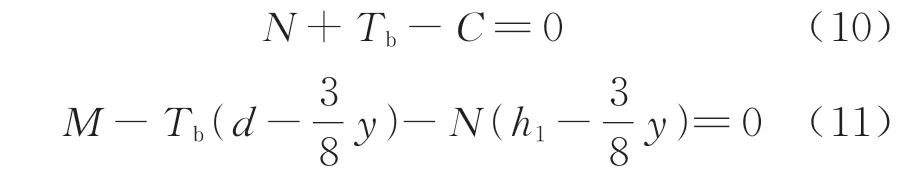
根据假设，受压区混凝土的压应力分布图为二次抛物线，且顶点位于受压区边缘处，故有

由混凝土变形关系及相关假设，受压区边缘混凝土的变形δc为

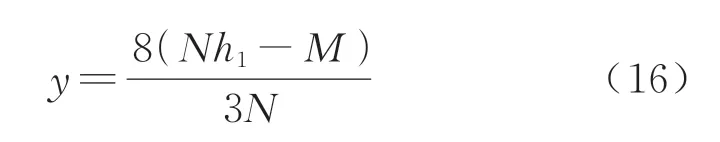
根据管片接缝处所受轴力N及弯矩M，由式（16）可求解出接缝处的受压区高度y，然后将所求y代入式（15），即可求解出接缝处应力σc，进而根据式（14）可求解出接缝转角θ.

根据假设，螺栓处接缝面混凝土仍受压的临界状态为受压区高度y=d.因此可以给定螺栓处混凝土受压的临界状态判定公式为

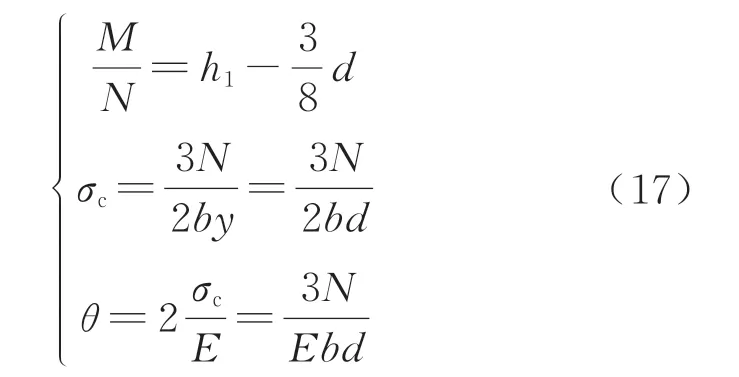
1.2.3 螺栓以上部分核心混凝土受压阶段

当接头张开度进一步发展，混凝土受压区将跨过螺栓，使得螺栓开始受拉，此时的混凝土受压区高度范围为0＜y＜d，受力分析如图3所示.

图3 螺栓以上部分核心混凝土受压模型计算简图Fig.3 Calculation schematic diagram at the compressionstage of the partial core concrete above bolts

从图3可知，该阶段与上阶段的区别仅在于螺栓参与承力，根据假定可知螺栓处接头面张开量δb为

由螺栓变形的物理关系得

式中：k表示螺栓刚度，联立式（14）、式（18）及式（19），并令

在该受力阶段中存在一临界状态，使得外缘混凝土接触，根据相关假设，当外缘混凝土刚接触时应满足条件

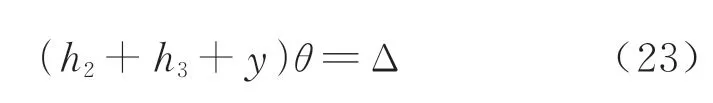
联立式（18）及式（23），可得

联立式（23）、式（24），可得外缘混凝土接触时核心混凝土受压区高度为

式中：h2、h3分别表示外缘混凝土厚度及密封衬垫嵌缝宽度.

1.2 .4外缘与核心混凝土共同承压阶段

随着外荷载的继续增大，接缝的外弧面将继续压紧，外缘混凝土参与承压，与核心混凝土共同工作.此阶段核心混凝土受压区高度进一步减小，外缘混凝土受压区高度逐渐增大，直至外缘混凝土超过承载力极限.该阶段体现了接缝构造形式对接缝受力特性的影响，其力学分析的影响因素较多，针对该阶段本文重点分析了外缘混凝土压碎时的临界力学性能，并引入了外缘混凝土受压区高度调整系数α，认为该系数与外缘混凝土高度h2的乘积即为外缘混凝土压碎时外缘混凝土受压区高度，该状态的受力分析如图4所示.

图4 外缘混凝土压碎时模型计算简图Fig.4 Calculation schematic diagram when the outer concrete is crushed

根据受力图建立相应的力学平衡为

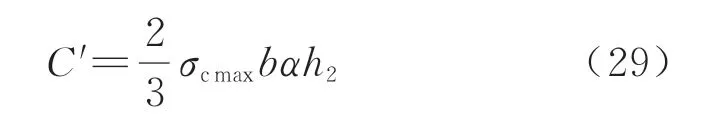
式中：C′表示外缘混凝土压应力合力；σcmax表示混凝土的抗压强度，根据假设及变形关系可知，外缘混凝土及核心混凝土受压区边缘的压缩变形分别为

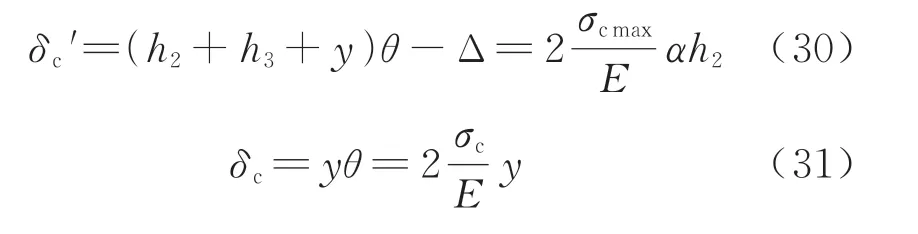
同理，螺栓处接头面张开量及螺栓变形为

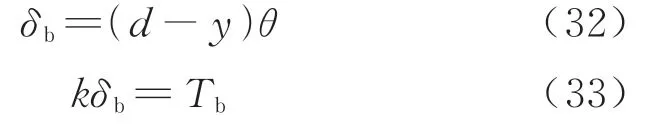
联立式（26）～式（33），并令β=2σcmaxαh2+EΔ，可得

由以上分析可知，在该受力阶段当确定了外缘混凝土受压区高度调整系数α后即可求出外缘混凝土压碎时，核心混凝土受压区高度y，然后再分别根据式（34）～式（37）可求解出此时θ、Tb及σc.

2 外缘受压区高度调整系数α

2.1 α计算方案

在盾构管片纵缝受力全过程理论分析中，外缘混凝土与核心混凝土共同承压阶段需明确外缘混凝土压碎时外缘混凝土受压区高度调整系数α，进而才能确定该阶段管片纵缝的力学性能.α受多因素影响，为明确不同工况下α的取值，利用有限元软件建立盾构管片纵缝承压的三维实体模型，对系数α的相关影响因素进行正交分析，选取五因素四水平正交表L16（45）进行正交分析，选取的影响因素及水平见表1.

表1 正交分析因素水平表Tab.1 Factor levels for orthogonal analysis

计算模型依据目前地铁盾构隧道常用管片形式建立，接缝采用5.8级M30直螺栓连接，混凝土等级C50，衬砌环外径6.4 m，内径5.8 m，幅宽1.2 m，忽略定位槽、定位棒及弹性密封垫的影响，见图5，图5中，螺栓长度为2t.由于管片为对称结构，因此为简化计算，计算模型取为管片幅宽方向的半结构并设置对称面进行分析，计算模型接缝面几何尺寸如表2所示.

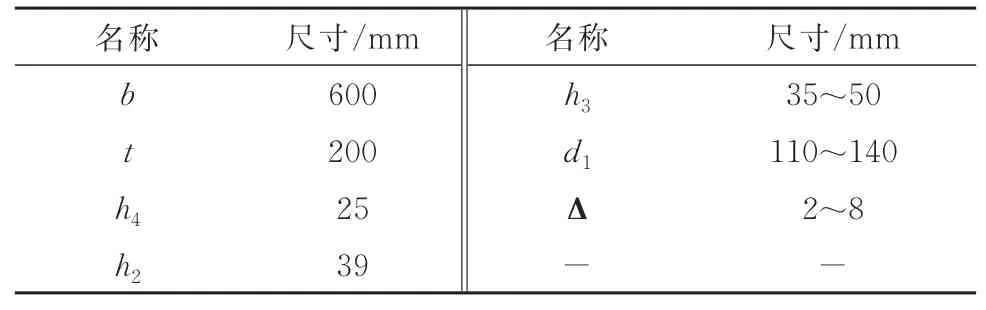
表2 混凝土管片几何参数表Tab.2 Geometric parameters of the segment mm

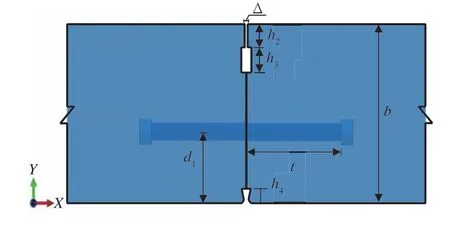
图5 管片接缝数值模型及剖面图Fig.5 Numerical model and sectional view of the segment joint

模型中混凝土与螺栓均采用弹性本构，模型中螺栓与螺栓孔、管片与管片间设置摩擦接触，摩擦系数分别取为0.55和0.15.模型前后面为对称面，并设置对应的对称边界，左右两侧底部的约束为简支.模型接头处各管片设置弯矩M，并分别与接缝处各管片界面运动耦合，不同工况下弯矩值均取为600kN·m，模型的左右侧面受到面荷载轴力N的作用，轴力N的取值需依据不同工况中的M/N来确定.模型计算共分两个荷载步进行，首先在第一步均匀施加管片轴力至最大值，然后保持轴力不变进行第二步管片弯矩的施加，直至管片破坏.

2.2 α影响因素分析

选取五因素四水平正交表L16（45）进行正交模拟分析，具体各组模拟参数及外缘混凝土受压区高度调整系数α如表3所示，其中空白列作为误差列，以定量分析各因素对模拟结果的影响程度.

表3 模拟正交表及模拟结果Tab.3 Simulation orthogonal and simulation results

对正交表模拟数据进行极差分析，确定各影响因素的优水平、最优水平组合及主次顺序，分析结果列于表4.其中，K1～K4为各因素不同水平下模拟结果总和的平均值，其大小可以判断各因素的优水平及模拟的优组合.R为各因素的极差，模拟结果的变动幅度可通过该列因素的极差反映，R越大说明该因素对模拟指标的影响越大，即该因素为主要影响因素.

由表4可知，接头空隙对外缘混凝土受压区高度调整系数α影响最大，其次是M/N、d1及h3，且在M/N为0.32，h3为50 m，d1为110 mm，Δ为4 mm的组合下，外缘混凝土受压区高度调整系数α达到最佳.

表4 极差分析Tab.4 Range analysis

为弥补极差分析不能区分因素各水平所对应模拟结果差异来源的不足，采用方差分析法对模拟数据进行进一步分析，以定量估计各因素对模拟结果的影响程度，方差分析结果列于表5.该正交表各因素自由度为3，将空白列作为误差列，则误差自由度为3，查F分布表可得F0.01（3，3）=29.46，F0.05（3，3）=9.28，F0.10（3，3）=5.36.M/N的F值FA=1.96＜F0.10（3，3），h3的F值FB=0.24＜F0.10（3，3），螺栓距管片内缘距离的F值FC=0.62＜F0.10（3，3），接头空隙的F值FD=20.33＞F0.05（3，3）.由方差分析结果可知：接头空隙对外缘混凝土受压区高度调整系数α具有强显著影响，M/N、密封衬垫嵌缝宽度h3及螺栓距管片内缘距离对外缘混凝土受压区高度调整系数α影响不显著.

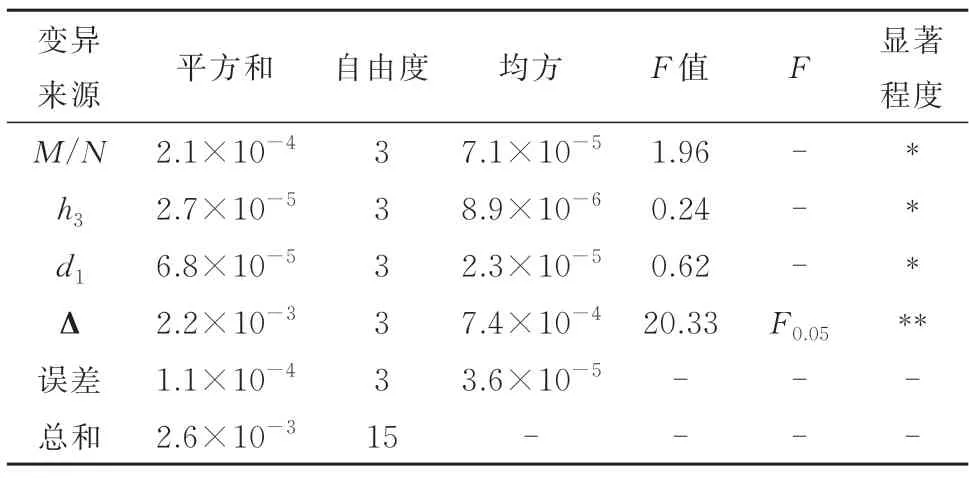
表5 方差分析Tab.5 Variance analysis

因此，综合考虑极差和方差分析结果可知，在分析各因素对外缘混凝土受压区高度调整系数α的影响时，可忽略M/N、h3及d1的作用效果，着重考虑接头空隙的影响.

“没关系的，”青辰道，“族人们很快就会发现咱们的失踪，他们很快就能找过来。最多傍晚，他们一定能找过来。”

为进一步分析外缘混凝土受压区高度调整系数α与接头空隙的关系，取M/N、h3及d1为最优水平，即M/N为0.32，h3为50 mm，d1为110 mm，接头空隙依据现有工程数据，取值范围设为1～10 mm，梯度取为1 mm，建立相应的数值模拟模型并进行计算，模型基本设置与正交分析模型设置相同，计算结果如图6.

图6 接头空隙与α关系图Fig.6 Relationship between joint gap andα

由以上分析可知，针对不同工况下外缘混凝土受压区高度调整系数α仅与接头间隙关系密切，并经过大量数值模拟，可初步建立α与接头间隙Δ的关系式为

我国地铁盾构隧道接头空隙一般处于2～6 mm，因此针对我国绝大多数地铁盾构隧道，α可近似取为0.2.

3 接头受力全过程理论解的验证

3.1 数值模型的建立

为验证盾构管片接缝受力全过程理论分析的合理性，依托北京某地铁盾构隧道管片尺寸，利用Abaqus有限元软件建立了盾构管片接缝受力三维实体模型.管片接缝采用5.8级M30直螺栓连接，弹性模量取为210 GPa，混凝土等级C50，其抗压强度为32.4 MPa，弹性模量取为3.45 GPa.衬砌环外径6.4 m，内径5.8 m，幅宽1.2 m，忽略定位槽、定位棒及弹性密封垫的影响.由于管片为对称结构，因此为简化计算，计算模型取为管片幅宽方向的半结构并设置对称面进行分析，接缝面几何尺寸见图7.

图7 数值模型接头基本尺寸（单位：mm）Fig.7 Basic dimensions of joint numerical model(Unit:mm)

模型中混凝土与螺栓均采用弹性本构，模型的接触、边界条件及荷载施加方式均与正交分析中的模型设置一致.该模型接头处各管片的弯矩M取为600 kN·m，轴力N取为600 kN.

3.2 理论与模拟验证结果

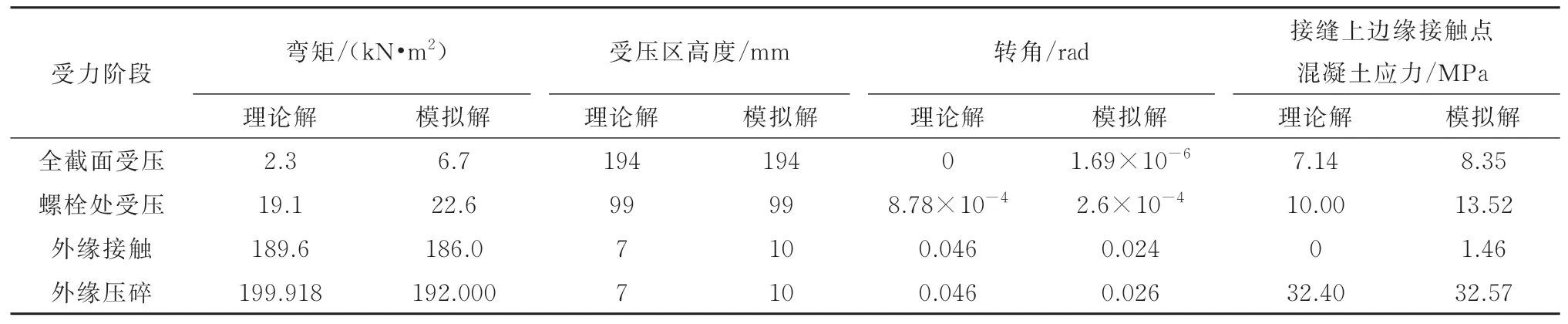
表6 接缝受力全过程各阶段典型理论与模拟值Tab.6 Typical theory and simulation values of all stages in joint stress process

为明确数值模拟结果的准确性，选取文献［7］中接头压弯试验数据结果，如图8所示.由于接头受力特性的影响因素众多，文献［7］中各试验条件与本文有所差异，造成试验结果与模拟结果的定量分析差异性较大，但接头受力特性的试验结果与模拟结果的变化规律具有一致性，因此可认为本文的数值模拟结果具有合理性.

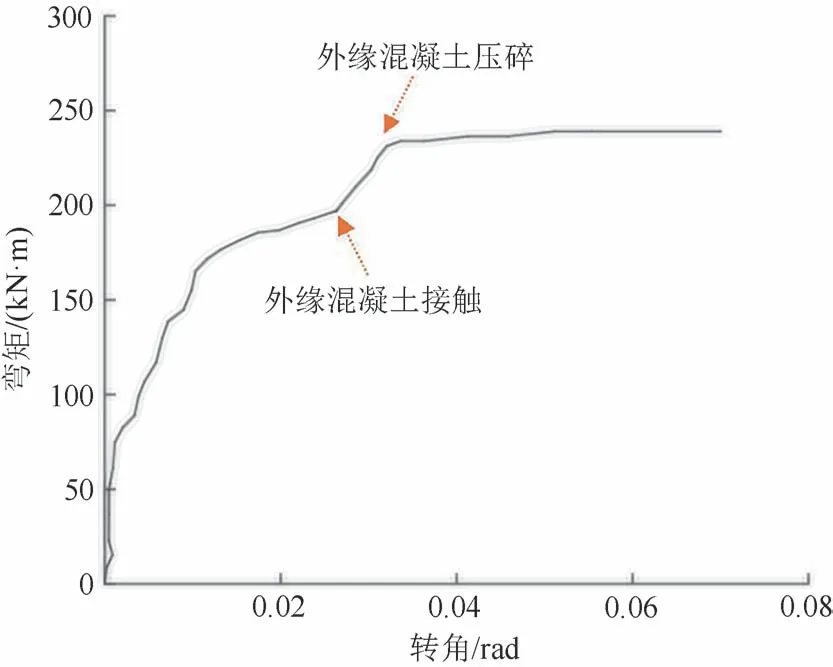
图8 管片接头试验的弯矩-转角变化关系[7]Fig.8 Relationship between bending moment and angle of segment joint in the test[7]

为进一步分析数值模拟结果与理论解的差异性，将管片接缝受压区高度及转角随弯矩变化曲线绘制如图9所示.由图9可知，理论与模拟的变化趋势整体一致，验证了理论解的可靠性.在螺栓未发挥作用时，理论推导与模拟结果变化规律一致，整体来看，螺栓未发挥作用前，理论推导结果对于隧道结构来说是偏于安全的.当螺栓产生拉力后，其对管片接缝的进一步张开具有抑制作用，螺栓孔附近混凝土压力较大形成应力集中区，管片接缝界面难以保持平截面.此阶段理论推导中的平截面假定与实际情况相差较大，从而造成螺栓明显受力后管片接头抗弯刚度的理论解比模拟值要小，且受压区高度理论解要小于模拟值.综合分析螺栓明显受力后管片接头的力学性能，理论解对于隧道结构来说偏于安全，且理论解能够较好地推导出管片接头的承载性能.因此，本文推导的盾构管片纵缝螺栓连接压弯承载力的理论模型能够较好地计算出接头承压全过程的力学性能，从而可为管片接头设计和管片接头病害预警及处理提供理论依据.