注浆主动控制隧道水平变形的机理及策略研究
2023-01-18林晓峰郑荣国程雪松盛鲁腾
林晓峰,郑荣国,郑 刚,程雪松,潘 军,盛鲁腾
(1.浙江杭海城际铁路有限公司,浙江 嘉兴 314499;2.浙江金温铁道开发有限公司,浙江 温州 325011;3.天津大学a.建筑工程学院,b.滨海土木工程结构与安全教育部重点实验室,天津 300072)
随着城市化进程的快速推进,城市人口越来越多,城市空间也愈发紧张.为加大空间的利用率和缓解城市交通压力,各大、中城市兴起了建设地铁的热潮.为开发地下空间而进行的基坑施工不可避免地引起周边土体产生变形,从而引发土体中隧道产生变形.这给地铁线路的结构安全和运营安全带来威胁,也对基坑设计水平及施工技术带来新的挑战.
基坑施工容易引起邻近既有隧道产生大变形,甚至威胁到地铁线路的结构安全和运营安全,因此我国国家标准和行业规范规定了严格的隧道变形控制标准.文献[1]中规定地铁结构设施绝对沉降量及水平位移量≤20 mm.文献[2]规定邻近施工引起的隧道水平位移和竖向位移预警值为10 mm,控制值为20 mm.文献[3]提出隧道结构沉降控制值为3~10 mm,隧道结构隆起控制值为5 mm,隧道结构水平位移控制值3~5 mm.地铁隧道变形控制标准逐渐严格化、全面化,控制要求由厘米级进入毫米级.因此针对基坑施工引起隧道变形的控制措施应具有精细控制的特点.
注浆为精细化主动控制隧道变形的常用方法[4-7].文献[5]通过现场测量和对多排注浆顺序和注浆参数进行的敏感研究发现,通过注浆可使隧道收敛面积平均减少25%,在相应地面条件下,移动至距隧道不小于3.0 m的隧道两侧进行对称注浆是实际注浆的最佳选择.文献[6]采用微扰动注浆法对隧道变形进行了修正.结果表明,变形隧道分别经过校正阶段和回弹阶段,通过微扰动注浆可以减少相邻开挖引起的附加变形.此外,注浆广泛用于控制建筑物、隧道和管线沉降[8-10].逄铁铮[11]为保证隧道穿越过程中既有地面建构筑物的安全,采取了地面注浆和洞内注浆的方法来进行过程控制和房屋抬升.文献[12]以北京地铁五号线崇文门地铁车站下穿既有线工程为研究对象,提出了根据既有线的沉降特征进行抬升注浆设计的方法.文献[13]通过研究注浆引起的土体体积膨胀的机制,将注浆体积、土体体积应变增量、位移大小三者联系在一起,提出了一种模拟注浆抬升地层的数值方法.文献[14]在分析建筑物沉降恢复特点的基础上研究注浆抬升机制,提出地层充填密实、止浆围护形成、抬升力形成及建筑物结构抬升的四阶段作用模式,并相应总结建筑物稳定抬升的施工技术要点.
目前有关注浆抬升既有建筑物或者隧道的研究较多,而有关注浆控制隧道水平变形的研究较少,且已有研究较多为工程案例分析,尚缺乏注浆对隧道水平变形进行控制的系统性机理与策略研究.因此,本文以天津市某大型基坑工程项目为背景,利用PLAXIS 3D有限元软件,建立三维有限元模型,系统研究隧道分别处于沉降区、过渡区和隆起区时[15]注浆控制隧道水平变形的机理及策略.为了更全面地评价注浆控制隧道变形的效果及影响,考虑隧道横向变形和纵向变形的恢复效果以及基坑支护体系的安全性,提出注浆效果综合评价体系.进一步,分析隧道分别处于沉降区、隆起区和过渡区时不同单位长度注浆量、注浆距离、相对注浆深度和注浆长度时竖直注浆对隧道和基坑支护体系的影响,并针对性提出实施建议,为今后注浆控制隧道变形的设计与实施提供支撑.
1 依托工程及三维有限元数值模型
1.1 数值模型的建立及验证
根据某大型基坑工程设计方案建立36 m宽的局部基坑三维有限元模型如图1所示.采用PLAXIS 3D进行数值模拟,有限元模型中C区基坑支护结构依据设计图纸建立,剖面图见图1(b),第1道、第2道、第3道支撑的横截面尺寸分布为0.8 m×1.2 m、1.0 m×1.2 m和1.0 m×1.2 m.立柱桩的直径为0.9 m,桩底深度为坑底以下20 m.A区基坑设计方案较为复杂,建立36 m宽局部基坑模型时,根据刚度等效原则,将支撑简化为板撑.有限元三维模型尺寸如图1(c)所示,边界条件为侧向边界约束水平位移和底部边界固定.土层分布及参数见表1,其中γ为重度,c′为有效黏聚力,φ′为有效内摩擦角,Eref50为对应于参考围压Pref时标准排水三轴试验中土体的参考割线刚度,在PLAXIS中,默认Pref=100 kPa;E为对应干参考围压Pref时固结试验中土体的参考切线刚度,E为对应于参考围压Pref时土体卸载/再加载的参考刚度,G为土体处于小应变状态时土体的参考剪切刚度.土体采用小应变硬化模型模拟,地下水位位于地表以下1.1 m.支撑、地连墙和隧道等结构采用线弹性模拟.隧道衬砌采用C50预制混凝土管片拼装而成,考虑到隧道纵向接头和环向接头的影响,隧道横向刚度有效率取为75%[16],隧道纵向刚度有效率取为20%[17].为考虑土体与结构的相互作用,在土体与结构之间生成12节点的界面单元.界面单元材料强度为相邻土体材料强度的0.67倍[18].
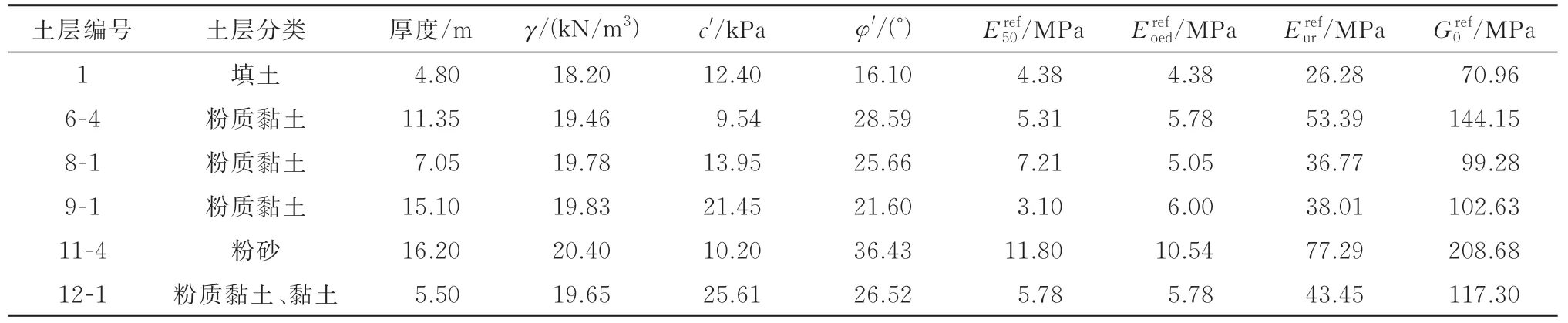
表1 土体物理力学参数Tab.1 Physical and mechanical parameters of soil

图1 三维有限元模型示意图Fig.1 Schematic diagram of 3D finite element model
基坑施工按照A区、B区、C区的顺序先后开挖,隧道内设置了4个监测点,左侧隧道监测点分别为L1、L2、L3、L4,右侧隧道监测点分别为R1、R2、R3、R4,如图1(b)所示.由于36 m宽模型没有考虑B区基坑,因此将实际工程中A区和C区基坑开挖引起的隧道变形之和与模拟结果进行对比,如图2(a)所示.由于只在R4测点处安装了静力水准仪,因此只有R4测点处隧道竖向位移的实测值,从而在图2(a)中只给出R4测点变形后的位置.右线隧道R1、R2、R3及R4测点的水平位移实测值分别为4.33、4.32、3.71及5.39 mm,模拟值分别为2.01、2.23、3.85、6.0 mm.由于实际工程中CX5测点从C区基坑第2层土方开挖前开始监测,未监测C区基坑第1层土方开挖引起的地连墙变形,因此将第2层至第4层土方开挖引起地连墙侧向变形实测结果与模拟结果进行对比,如图2(b)所示.实测与模拟结果基本一致,验证了模型的可靠性.

图2 隧道与地下连续墙变形的实测与模拟结果对比Fig.2 Comparison between measured and simulated results of deformation in tunnel and underground continuous wall
1.2 简化数值模型
为便于参数分析,将有限元模型进行简化,如图3所示.图3中D为注浆距离,即为注浆体中心到隧道腰部的净距;L为注浆区域沿深度方向的长度;H为相对注浆深度,即为注浆体中心线深度与隧道中心线深度的差值,浆体中心线深度比隧道中心线深度小时,相对深度为负值,反之为正值.隧道环的宽度为1.2 m,注浆孔沿隧道纵向上的布置方式一般是一个注浆孔对应一个隧道环,因此注浆孔沿隧道纵向上的间距为1.2 m.考虑7个注浆孔,从而模型宽度为8.4 m.为便于模拟,体现一排孔注浆效果的施加应变区域为8.4 m×1.2 m×L矩形区域,体现单孔注浆效果的施加应变区域为1.2 m×1.2 m×L.假定施加应变区域沿深度方向均匀膨胀.

图3 简化模型Fig.3 Simplified model
基坑开挖宽度为65 m,为提高计算效率,建立一半模型.基坑内支撑为对撑,沿隧道纵向上每8.4 m一根;靠近地铁侧立柱沿对撑方向为每5 m一根;基坑开挖深度取为16 m,且在4.8、9.2和12.7 m深处各设置1道混凝土支撑,支撑的横截面尺寸按照实际工程设置.隧道中心深度为16 m,隧道与基坑距离为1倍的基坑开挖深度,即16 m.模型土层简化为3个土层,分别为8-1粉质黏土、11-4粉砂和12-1粉 质黏土,3个土层的 厚 度分别为30、24.5和45.5 m.
基坑开挖后,隧道呈现为往基坑方向斜向上的椭圆形状,隧道水平位移最大值为12.4 mm,隧道最大隆起值为6.1 mm.由于第1道支撑设置在4.8 m深处,基坑开挖完成后地连墙侧向变形呈现复合型变形模式,地连墙最大水平位移为32.4 mm.
2 注浆效果综合评价体系
以往评价注浆效果时,主要根据隧道位移的恢复率.但仅考虑隧道位移,无法综合地评判隧道的变形情况,隧道除了位移之外,也会发生形变(即椭圆度会发生变化).此外,在注浆恢复基坑引发的隧道位移时,注浆对基坑也会产生一定的不利影响,因此为了保证基坑安全,也需要考虑注浆对基坑的影响.因此,在进行系统研究之前,本文综合考虑了注浆对既有隧道和基坑的影响,建立注浆对隧道及基坑支护结构变形影响的综合评价体系.
隧道变形可分解为刚体位移和形变.仅针对单环隧道,刚体位移对隧道变形及受力不产生影响.刚体位移为隧道中心点的位移,包括水平位移和竖向位移,为一个矢量位移.某一单个隧道环刚体位移会影响隧道沿纵向上的挠曲,从而引起隧道环间错台、纵向螺栓受力增大等不利情形.因此可采用隧道刚体位移恢复率评价注浆恢复隧道纵向挠曲的效果.
此外,对于单个隧道环,形变会影响隧道管片受力、环向接头张开、环向螺栓受力情况.因此对于单个隧道环,最重要的评价指标是形变.形变可用椭圆度表示,因此可采用椭圆度恢复率评价注浆恢复隧道横向形变的效果.
注浆使隧道变形恢复到基坑开挖前的变形最为合理.在设计注浆方案时,需要尽可能地使隧道的刚体位移和形变恢复到基坑开挖之前的状态.此外,隧道左右腰部的水平位移、顶部和底部的竖向位移也是关注对象,这些在隧道水平及竖向刚体位移的指标中已有体现.隧道水平收敛和竖向收敛也是工程中较为容易监测得到的数据,其在隧道椭圆度的指标中已有体现.因此,对于隧道变形,隧道水平刚体位移恢复率、隧道竖向刚体位移恢复率、隧道椭圆度恢复率作为主控指标,隧道左右腰部水平位移恢复率、顶部和底部竖向位移恢复率、水平收敛恢复率作为辅控指标.同时,注浆会对基坑支护结构产生影响,因此基坑地下连续墙水平位移增长率、弯矩增长率、支撑轴力变化率也作为辅控指标.
2.1 注浆效果主控指标
1)隧道水平刚体位移恢复率.
隧道水平刚体位移恢复率为注浆引起的隧道水平刚体位移与基坑开挖引起的隧道水平刚体位移之比,可评价在水平方向上注浆恢复隧道纵向挠曲的效果.隧道水平刚体位移表达为隧道中心点刚体位移,可在实际工程中取为隧道两侧腰部水平位移的平均值.
2)隧道竖向刚体位移恢复率.
隧道竖向刚体位移恢复率为注浆引起的隧道竖向刚体位移与基坑开挖引起的隧道竖向刚体位移之比,可评价在竖直方向上注浆恢复隧道纵向挠曲的效果.隧道竖向刚体位移表达为隧道中心点刚体位移,可取为隧道顶部和底部竖向位移的平均值.
3)隧道椭圆度恢复率.
椭圆度是评价隧道横向变形的常用指标,表达为
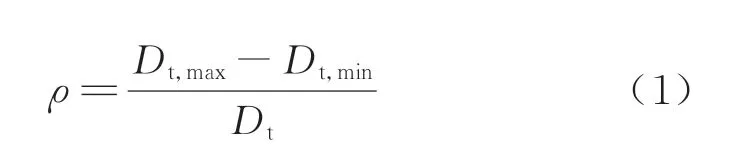
式 中:Dt,max和 为Dt,min分别为隧道直径的最大值和最小值;Dt是隧道设计外径,为6.2 m.
隧道椭圆度恢复率ηρ为注浆引起的隧道椭圆度恢复量与基坑开挖引起的隧道椭圆度增量之比,表达为

式中:ρg和ρe分别为注浆和基坑开挖引起的隧道椭圆度变化量.
隧道水平刚体位移恢复率、竖向刚体位移恢复率和椭圆度恢复率小于0时,说明注浆使隧道变形增大,具有不利作用;这些指标大于0且小于或等于1时,说明注浆具有变形恢复效果,且指标值越接近1,注浆效果越好;这些指标大于1,说明注浆过量恢复了隧道变形,也具有不利作用.
2.2 注浆效果辅控指标
1)隧道辅控指标.
隧道左右腰部水平位移恢复率、顶部和底部竖向位移恢复率、水平收敛恢复率、竖向收敛恢复率分别为注浆引起的隧道变形量值与基坑开挖引起的隧道变形量值之比.隧道水平及竖向刚体位移恢复率主要反映了隧道水平及竖向上纵向挠曲恢复的效果,而水平刚体位移取决于隧道左右腰部水平位移,竖向刚体位移取决于隧道顶部和底部竖向位移.因此隧道左右腰部水平位移恢复率、顶部和底部竖向位移恢复率均可一定程度上反映隧道刚体位移恢复率,但不及隧道水平及竖向刚体位移恢复率准确及全面.同样,水平收敛恢复率、竖向收敛恢复率均可反映隧道的形变恢复量,但其不及隧道椭圆度恢复率全面及表达简便.
2)地下连续墙辅控指标.
地下连续墙水平位移增长率、弯矩增长率、支撑轴力变化率为注浆引起的变形或受力增量与基坑开挖引起的变形或者受力值之比.
对于隧道左右腰部水平位移恢复率、顶部和底部竖向位移恢复率、水平收敛恢复率、竖向收敛恢复率,这些指标越接近1,表明注浆效果越好.而对于地下连续墙水平位移增长率、弯矩增长率、支撑轴力变化率,这些指标越接近0,表明注浆对基坑支护结构的影响越小.
3 隆起区注浆控制水平变形
3.1 注浆距离的影响
8.4m宽模型中包含7个注浆孔,模拟7个孔同时注浆,每个孔注浆量相同.注浆距离D取为1、3、5、8和12 m,注浆长度L取为5 m.相对注浆深度H取-3、-2、-1、0、1 m.根据现场试验和注浆应用的经验,单孔注浆量取为0.3、0.45、0.6、0.75和0.9 m3.为便于改变注浆长度,将总注浆量换算为沿竖向上单位长度注浆量.总注浆量0.3、0.45、0.6、0.75和0.9 m3与沿竖向上单位长度注浆量0.06、0.09、0.12、0.15和0.18 m3/m一一对应,将沿竖向上单位长度注浆量均简称为注浆量V.研究注浆距离的影响时,相对注浆深度H固定为-1 m.粉质黏土中注浆影响区域体积膨胀量与注入浆液体积的比例与土质情况、注浆方式、浆液性质密切相关,参考文献[8-9,19]的分析结果,此次模拟中注浆影响区域体积膨胀量与注入浆液体积的比例取为35%.
选取单位长度注浆量为0.15 m3/m时注浆引起隧道和地下连续墙变形作为典型案例,以分析不同注浆距离时注浆对隧道和基坑的影响.图4为不同注浆距离时注浆引起隧道变形和地下连续墙侧向变形对比分析.由图4可知,基坑开挖完成后隧道变形呈现往基坑方向斜向上的椭圆形状,隧道水平位移最大值为12.4 mm,位置在于隧道中心线偏上0.4 m,即15.6 m深处;开挖后隧道竖向位移最大值为6.1 mm,位于隧道底部.注浆后,在D=12 m到D=1 m过程中,隧道水平位移和隧道竖向位移最大值不断减小,且减小速度越来越快,分别减小至6.4 mm和4.1 mm.此外,基坑开挖完成后隧道顶部竖向位移为1.6 mm.注浆后,在D=12 m到D=1 m过程中,隧道顶部竖向位移不断增大,且增大速度越来越快,最终增大至4.8 mm.对于地下连续墙水平位移,基坑开挖完成后地下连续墙水平位移最大值为32.4 mm.D为1、3、12 m时,注浆分别使地下连续墙最大水平位移增大至34.7、35.3和36.6 mm.开挖完成后,第1至第3道支撑轴力分别为4 854、6 813和6 289 kN.注浆引起第1道支撑轴力减小,引起第2道和第3道支撑轴力增大.注浆距离D为3 m时,注浆后第1道支撑轴力减小至4 807 kN,第2道和第3道支撑轴力分别增大至7 694 kN和8 432 kN.

图4 隧道变形和地下连续墙侧向变形随D的变化规律Fig.4 Variation law of tunnel deformation and lateral deformation of diaphragm wall with grouting distance
1)对隧道变形的影响.
图5为隧道右腰部水平位移恢复量在不同注浆距离下的变化规律,其中隧道右腰部为靠近基坑侧腰部.随着注浆距离的增大,注浆引起的隧道水平位移恢复量逐渐减小,且注浆量越大,恢复效果越好.单位长度注浆量为0.06~0.18 m3/m时,隧道右腰部水平位移恢复量在0.7~9.8 mm之间.图6为隧道刚体位移位移恢复量在不同注浆距离下的变化规律,注浆引起隧道水平刚体位移恢复量随注浆距离的变化规律与注浆引起隧道右腰部水平位移恢复量的变化规律基本一致,但隧道水平刚体位移恢复量小于隧道右腰部水平位移恢复量,其原因是注浆对隧道左腰部水平位移的影响较小.图6(b)恢复量为负值,表示注浆引起隧道进一步发生更大的隆起变形.

图5 隧道右腰部水平位移恢复量随注浆距离的变化规律Fig.5 Variation law of horizontal displacement recovery in right lumbar of tunnel with grouting distance
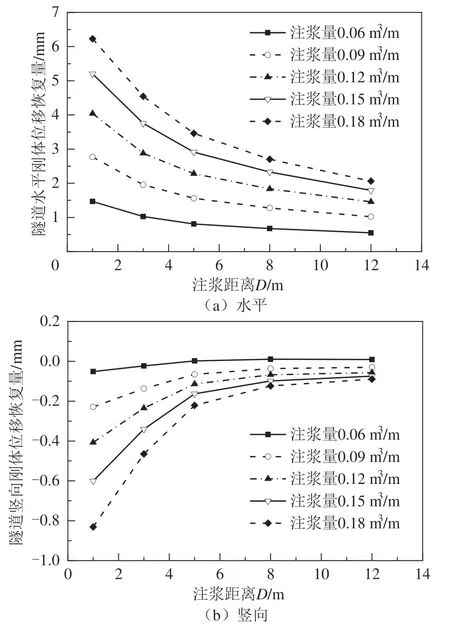
图6 隧道刚体位移恢复量随D的变化规律Fig.6 Variation law of tunnel rigid body displacement recovery with grouting distance
注浆引起隧道顶部和底部竖向位移变化规律主要由隧道受浆液横向挤压决定.注浆后,由于浆液横向上挤压隧道,注浆引起隧道顶部隆起,而引起隧道底部下沉.且隧道顶部的隆起量大于隧道底部的下沉量,其原因是隧道底部土体应力水平更大,如图7所示.整体而言,注浆引起隧道竖向变形较小.

图7 隧道竖向位移恢复量随D的变化规律Fig.7 Variation law of tunnel vertical displacement recovery with grouting distance
图8为隧道椭圆度在不同注浆距离下的变化规律,单位长度注浆量在0.06~0.09 m3/m之间时,注浆位置与隧道越近,注浆后隧道的椭圆度越小.当单位长度注浆量为0.15~0.18 m3/m之间,注浆距离D小于3 m时,注浆引起隧道的椭圆度增大,其原因是注浆引起隧道发生过大的局部变形,见图4.不同注浆距离下的椭圆度恢复率如图9所示,注浆后隧道椭圆度恢复率最高达到89%,恢复率较高.

图8 注浆后隧道椭圆度随D的变化规律Fig.8 Variation law of tunnel ovality with grouting distance after grouting
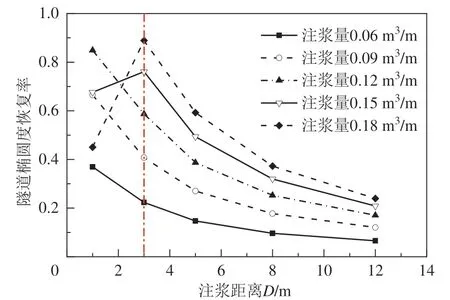
图9 隧道椭圆度恢复率随注浆距离的变化规律Fig.9 Variation law of tunnel ovality recovery rate with grouting distance
当注浆距离小于3 m时,注浆容易过度挤压隧道,引起隧道椭圆度增大,不利于隧道横断面的变形及受力;当注浆距离大于3 m时,随着距离增大,椭圆度越来越大,椭圆度恢复率越来越小.因此,建议注浆距离为3 m,此时隧道的水平刚体位移恢复量和椭圆度恢复率均较大,注浆综合效果较好.
2)对基坑支护结构的影响.
图10为地下连续墙水平位移增大率在不同注浆距离下的变化规律,选择注浆量为0.15 m3/m的情形作为代表.注浆距离D为1 m、3 m和12 m时地连墙水平位移增大率分别为0.07、0.09和0.13.随着注浆距离的增大,即注浆位置与地下连续墙越来越近,注浆对地连墙的影响越来越大.

图10 注浆引起地下连续墙水平位移增大率随D的变化规律Fig.10 Variation law for increment rate of grouting-led horizontal displacement in diaphragm wall with grouting distance
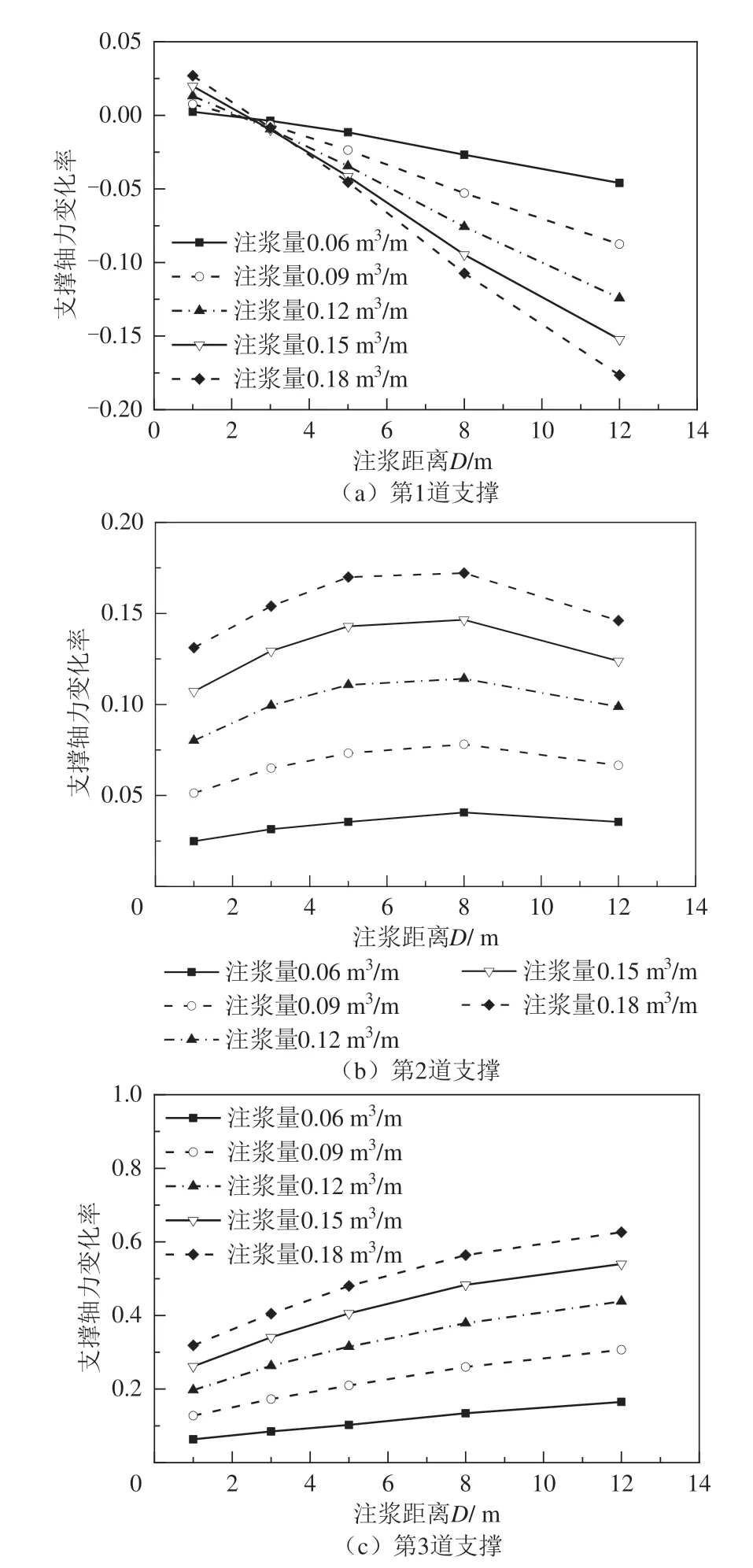
图11 第1至第3道支撑轴力变化率随D变化规律Fig.11 Variation law of axial force in first to third support with grouting distance
图11为第1至第3道支撑轴力变化率随注浆距离变化规律,注浆位于坑底附近,注浆之后,坑底处地连墙水平变形增大,但注浆距离大于3 m时,第1道支撑处地连墙水平位移减小,因此当注浆距离超过3 m时注浆引起第1道支撑轴力减小,且注浆位置与地连墙越近,注浆量越大,支撑轴力减小越显著,见图11(a).当注浆距离为1 m(注浆位置与地下连续墙的距离为15 m)时,注浆反而引起第1道支撑轴力增大,其原因是注浆位置与地连墙较远时,注浆的深度影响范围较大,注浆使得第1道支撑处地连墙变形增大,使第1道支撑的受力也增大.
如图11(b)所示,注浆引起第2道支撑轴力增大,注浆量越大,轴力增大越显著.此外,随着注浆体与隧道距离的增大,第2道支撑轴力的增大率先增大后减小.当注浆距离较小(注浆体与隧道较近)时,注浆对第2道支撑的影响较小;当注浆距离较大时(注浆体与地连墙较近)时,注浆引起坑底处地连墙变形较大,由于地连墙变形协调,第2道支撑的增大率反而减小.因此,当注浆体处于隧道与地连墙中间位置时,注浆对第2道支撑的影响最大.如图11(c)所示,注浆引起第3道支撑轴力增大,注浆位置与地连墙越近,注浆量越大,支撑轴力增大越显著.
整体而言,注浆对第1道和第2道支撑的影响较小.当注浆量为0.15 m3/m至0.18 m3/m且注浆体与地连墙距离小于4 m时,注浆使第3道支撑轴力增大超过50%,会对支撑安全造成威胁.因此,不宜在与地连墙较近(如小于4 m)进行大方量(如超过0.15 m3/m)注浆.
3.2 相对注浆深度的影响
注浆距离D固定为3 m,注浆长度L固定为5 m,相对注浆深度H为-3至1 m,注浆量为0.06、0.09、0.12、0.15和0.18 m3/m.注浆位置与隧道相对关系示意图见图12.

图12不同相对注浆深度时注浆位置示意图Fig.12 Schematic diagram of grouting position at different relative grouting depths
图13 为注浆量为0.15 m3/m时不同相对注浆深度情形下注浆后隧道变形对比.注浆体在隧道右偏上的位置时,浆液膨胀使隧道受到左向下的挤压作用;而注浆体在隧道右偏下的位置时,浆液膨胀使隧道受到左向上的挤压作用.相对注浆深度变化时,隧道所受到的水平向挤压作用仍然比所受到的竖向挤压作用更为显著.

图13 注浆量为0.15 m3/m时不同相对注浆深度情形下注浆后隧道变形对比(隧道变形放大200倍)Fig.13 Comparison of tunnel deformation after grouting under different relative grouting depths at 0.15 m3/m grouting volume(tunnel deformation amplified 200 times)
1)位移恢复率变化.
图14为隧道水平刚体位移恢复率在不同相对注浆深度下的变化规律,注浆体逐渐下移时,隧道水平刚体位移恢复率先增大后减小.当相对注浆深度在-1至0 m之间时,隧道水平刚体位移恢复率最大.基坑开挖后隧道发生右向上的变形,隧道最大水平位移位于隧道中心线以上0.4 m处,当相对注浆深度为在-1至0 m之间时,浆液膨胀对隧道的挤压作用最为显著.

图14 隧道水平刚体位移恢复率随H的变化规律Fig.14 Variation law for recovery rate of horizontal rigid body displacement in tunnel with relative grouting depth
图15为隧道竖向刚体位移恢复率随相对注浆深度的变化规律.基坑开挖后隧道产生隆起变形,注浆引起隧道隆起量增大,因此恢复率为负值.负值越小,表明注浆引起隧道隆起量越大.注浆体逐渐下移时,注浆引起隧道隆起变形的增量先增大再减小.整体而言,注浆对隧道竖向变形的影响较小.

图15隧道竖向刚体位移恢复率随H的变化规律Fig.15 Variation law for recovery rate of vertical rigid body displacement in tunnel with relative grouting depth
图16为隧道顶部和底部竖向位移恢复率在不同相对注浆深度下的变化规律,对于隧道顶部,基坑开挖后隧道顶部产生隆起变形,而注浆后隧道顶部的隆起变形更大,因此注浆对隧道顶部竖向位移具有不利作用,即隧道顶部竖向位移恢复率为负值.注浆位置逐渐下移时,注浆引起隧道顶部隆起量先增大后减小.注浆体在隧道中心线偏上位置时,注浆对隧道有下压作用,但同时注浆体会在横向上挤压隧道,使隧道顶部隆起,因此,即使注浆体处于隧道中心线偏上位置时,注浆仍引起隧道顶部隆起.当相对注浆深度为0 m时,注浆引起隧道顶部隆起变形的增量最大,其原因是此时注浆对隧道的横向挤压最明显.而注浆体移至隧道中心线偏下位置时,尽管注浆对隧道有抬升作用,但挤压作用比抬升作用更为显著,因此注浆体移至隧道中心线偏下位置时,挤压作用减小,从而隧道顶部隆起变形的增量减小.

图16 隧道顶部和底部竖向位移恢复率随H的变化规律Fig.16 Variation law for recovery rate of vertical displacement at top and bottom of tunnel with relative grouting depth
对于隧道底部,基坑开挖后隧道底部产生隆起变形,而注浆后隧道底部的隆起变形减小,因此注浆对隧道底部竖向位移具有有利作用,即隧道底部竖向位移恢复率为正值.注浆位置逐渐下移时,注浆引起隧道底部下沉量逐渐增大,当相对注浆深度大于0 m时,注浆引起隧道底部下沉量基本不变.注浆体在隧道中心线偏上位置时,注浆对隧道有下压作用,同时注浆体会横向上挤压隧道,使隧道底部产生沉降.当相对注浆深度为0 m时,注浆引起隧道底部下沉量最大,其原因是此时注浆对隧道的横向挤压最明显.而注浆体移至隧道中心线偏下位置时,注浆对隧道的抬升作用使隧道底部隆起,同时浆液横向上挤压隧道,使隧道底部下沉.注浆体下移时,抬升作用逐渐增大,挤压作用逐渐减小.因此,与相对注浆深度为0 m时相比,相对注浆深度为1 m时注浆引起隧道底部下沉量基本保持不变.
整体而言,注浆引起隧道竖向变形的规律主要由2个因素决定:水平挤压作用、下压或者抬升作用,简称为推移作用.挤压作用使隧道顶部隆起,同时使隧道底部下沉.且由于隧道底部土体应力水平更高,隧道顶部隆起量大于隧道底部下沉量.随着注浆位置逐渐下移,挤压作用先增大后减小,在相对注浆深度为0 m(即注浆体中心线与隧道中心线保持平齐)时,挤压作用达到峰值.竖向作用由注浆位置决定,注浆处于隧道偏上位置时,注浆对隧道竖向上具有下压作用;注浆处于隧道偏下位置时,注浆对隧道竖向上具有抬升作用.挤压作用显著大于推移作用,因此,沿竖向上打设注浆孔时注浆后隧道顶部和底部分别呈现隆起和下沉变形.
2)椭圆度恢复率变化.
图17为隧道椭圆度恢复率在不同相对注浆深度下的变化规律,随着注浆体逐渐下移,隧道椭圆度恢复率先增大后减小,当相对注浆深度为-1 m时,隧道椭圆度恢复率达到峰值.基坑开挖后,隧道产生右向上的变形模式,因此注浆位置处于隧道右偏上1 m时,注浆对隧道横向变形的恢复最显著,也最均匀.此外,当相对注浆深度为0时,注浆对隧道腰部的挤压作用最显著,但此时隧道右上侧的变形并没有得到很好地恢复(见图13),因此此时隧道的椭圆度恢复率并不是最高.
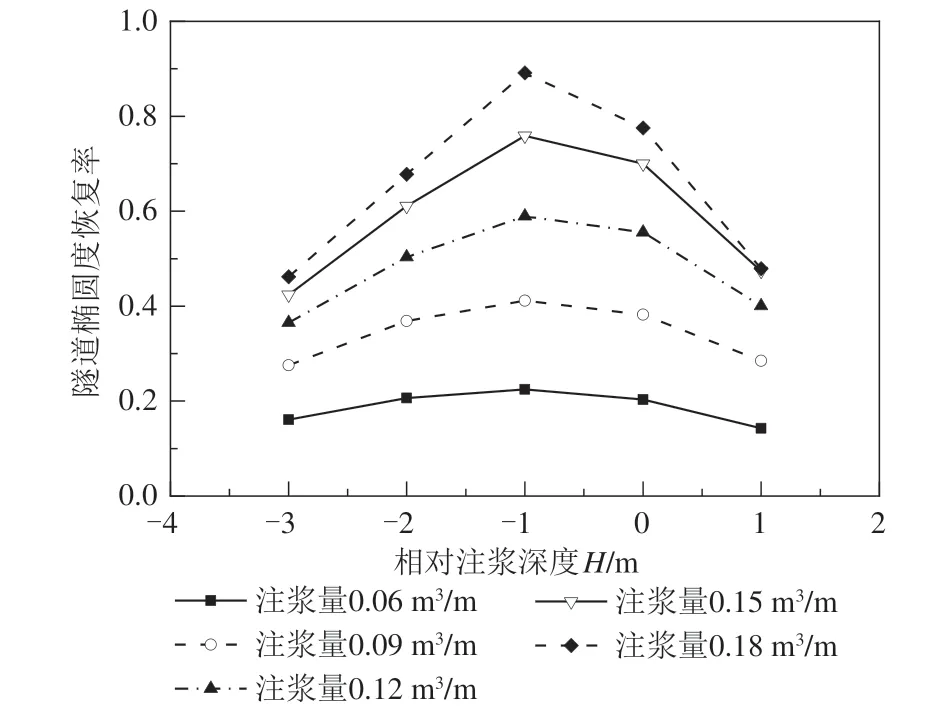
图17 隧道椭圆度恢复率随H的变化规律Fig.17 Variation law for tunnel ovality recovery rate with relative grouting depth
因此,当隧道处于基坑引发坑外变形的隆起区时,综合隧道水平刚体位移恢复率、竖向刚体位移恢复率和椭圆度恢复率等指标,建议注浆体中心线深度设计为隧道中心线偏上1 m处.
3.3 注浆长度的影响
根据注浆距离、相对注浆深度影响的研究结果,注浆距离保持在3 m,相对注浆深度保持在-1 m,而注浆长度为1、3、5、7、13 m时,注浆位置见图18.改变注浆体长度时,注浆体沿竖向上单位长度的注浆量保持不变.研究选取了5种沿竖向上单位长度注浆量,即0.06、0.09、0.12、0.15和0.18 m3/m.
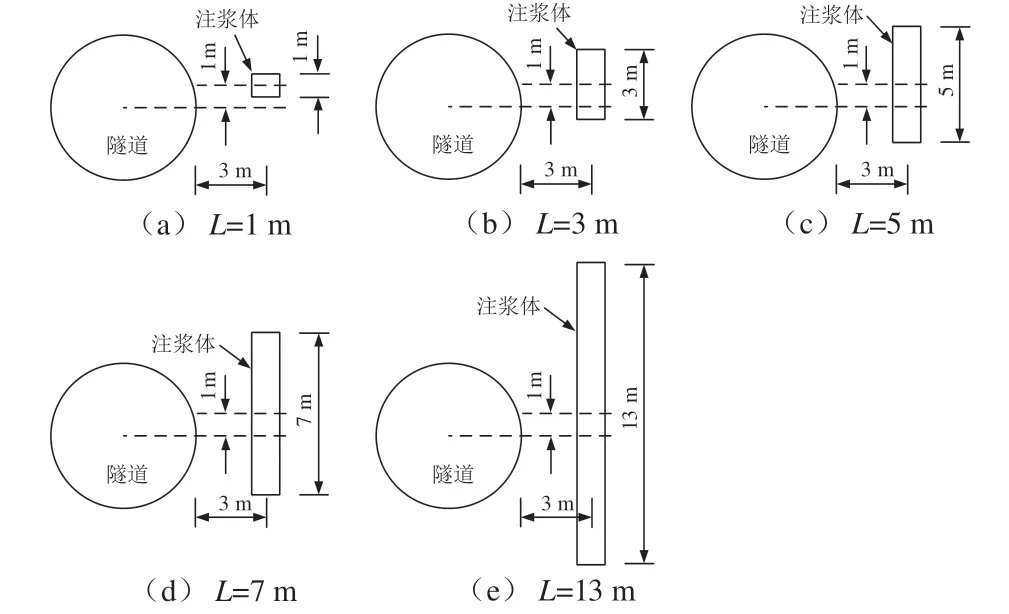
图18不同注浆长度时注浆位置示意图Fig.18 Schematic diagram of grouting position at different grouting lengths
图19为注浆量为0.15 m3/m的情形下不同注浆长度时注浆后隧道变形对比.随着注浆体长度的增大,总注浆量增大,浆液膨胀对隧道的挤压作用越来越明显.

图19注浆量为0.15 m3/m的情形下不同注浆长度时注浆后隧道变形对比(隧道变形放大200倍)Fig.19 Comparison of tunnel deformation after grouting at different grouting lengths with grouting volume of 0.15 m3/m(tunnel deformation amplified 200 times)
图20为隧道椭圆度恢复率随注浆长度的变化规律.当注浆量为0.06~0.15 m3/m时,随着注浆长度的增大,隧道椭圆度恢复率逐渐增大,且注浆长度由1 m增至5 m时,隧道椭圆度恢复率增长速度最快.当注浆长度大于7 m时,加大注浆长度对隧道椭圆度恢复率的增益效果不明显.注浆量为0.18 m3/m的情形下,随着注浆长度的增大,隧道椭圆度恢复率首先逐渐增大,直到注浆长度大于5 m时,隧道椭圆度恢复率逐渐减小,其原因是过长的注浆体已经对隧道产生了过度挤压(见图19),对隧道横向变形产生了不利的影响.整体而言,注浆长度取5~7 m可以取得注浆效果和经济上的平衡.

图20 隧道椭圆度恢复率随L的变化规律Fig.20 Variation law of tunnel ovality recovery rate with grouting length
4 沉降区、过渡区注浆控制水平变形
4.1 沉降区
当隧道处于沉降区,隧道整体表现为斜向下的变形模式,见图21.注浆距离和注浆长度对注浆效果的影响已在隧道处于隆起区时进行了大量的研究.隧道处于沉降区和过渡区时,注浆距离和注浆长度对注浆效果的影响与隧道处于隆起区的影响基本一致,进一步分析隧道处于过渡区和沉降区时相对注浆深度对注浆效果的影响.

图21 不同相对注浆深度时注浆后隧道变形对比Fig.21 Comparison of tunnel deformation after grouting at different relative grouting depths
注浆距离D固定为3 m,注浆长度L固定为5 m.注浆量为0.12、0.15及0.18 m3/m.相对注浆深度H为-1至3 m,注浆位置与隧道相对关系示意图见图12.
图22为隧道刚体位移恢复率在不同相对注浆深度下的变化规律,相对注浆深度为0 m时,隧道水平刚体位移的恢复率最大,其原因是基坑开挖后隧道呈现斜向下的变形模式.此外,注浆引起隧道隆起,因此注浆对隧道竖向变形具有恢复作用;挤压效应最显著时,注浆对隧道竖向变形的恢复效果也最好.如图23所示,相对注浆深度为0 m时,隧道椭圆度的恢复率最高.综合以上分析,隧道处于沉降区时,建议相对注浆深度为0 m.

图22 隧道刚体位移恢复率随H的变化规律Fig.22 Variation law for recovery rate of tunnel rigid body displacement with relative grouting depth

图23隧道椭圆度恢复率随H的变化规律Fig.23 Variation law for tunnel ovality recovery rate with relative grouting depth
4.2 过渡区
图24 为注浆量为0.12 m3/m的情形下不同相对注浆深度注浆后隧道变形对比.隧道处于过渡区时,隧道顶部下沉,隧道底部隆起,且隧道水平变形更大.图25为隧道刚体位移恢复率在不同相对注浆深度下的变化规律,相对注浆深度为0 m时,隧道水平刚体位移的恢复率最大.此外,注浆引起隧道隆起,因此注浆对隧道竖向变形具有恢复作用.由于基坑开挖引起的隧道竖向变形很小,基数很小,因此隧道竖向位移恢复率最大值达到11.6,即注浆过度恢复了隧道的竖向变形.但注浆对隧道竖向变形的影响依然很小.相对注浆深度为1 m时,注浆对隧道竖向变形的恢复效果最好.图26为隧道椭圆度恢复率在不同相对注浆深度下的变化规律,相对注浆深度为-1 m时,隧道椭圆度的恢复率最高.隧道水平刚体恢复率也很高,综合考虑建议隧道处于过渡区时相对注浆深度取为-1 m.

图24 注浆量为0.12 m3/m的情形下不同H时注浆后隧道变形对比Fig.24 Comparison of tunnel deformation after grouting at different relative grouting depths with grouting volume of 0.12 m3/m

图25 隧道刚体位移恢复率随H的变化规律Fig.25 Variation law for recovery rate of tunnel rigid body displacement with relative grouting depth
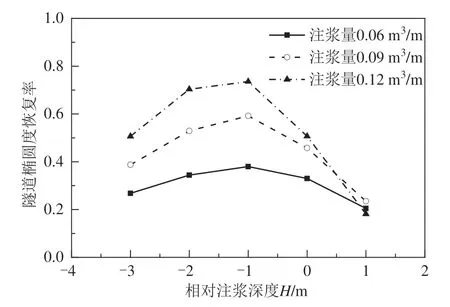
图26 隧道椭圆度恢复率随相对注浆深度的变化规律Fig.26 Variation law for tunnel ovality recovery rate with relative grouting depth
5 结 论
1)提出了注浆效果综合评价体系,解决了评价注浆效果时未全面考虑隧道的刚体位移和形变以及未考虑基坑安全性的问题.该综合评价体系以隧道水平刚体位移恢复率、竖向刚体位移恢复率和椭圆度恢复率为主控指标,以隧道左右腰部水平位移恢复率、顶部和底部竖向位移恢复率、水平收敛恢复率和地下连续墙水平位移增长率、地下连续墙弯矩增长率、支撑轴力变化率作为辅控指标.
2)在隧道侧方进行竖直注浆引起隧道竖向变形的规律由挤压作用和推移作用决定,挤压作用显著大于推移作用.注浆后隧道顶部和底部分别呈现隆起和下沉变形,由于隧道底部土体应力水平更高,隧道顶部隆起量大于隧道底部下沉量.
3)在隧道侧方进行竖向注浆时:当注浆距离小于3 m时,注浆容易过度挤压隧道,引起隧道椭圆度增大;当注浆距离大于3 m时,随着距离增大,椭圆度恢复率越来越小.综合考虑,建议注浆距离为3 m左右.考虑注浆效果和经济性,隧道直径6 m左右时,注浆体长度建议为5~7 m.
4)在隧道侧方进行竖向注浆时:当注浆位置与地连墙距离较大时,注浆引起第1道支撑处地连墙变形增大,使得支撑轴力增大;当注浆位置与地连墙距离较小时,注浆后坑底处地连墙水平变形增大,墙顶处水平位移减小,使得第1道支撑轴力减小,注浆位置与地连墙越近,注浆量越大,支撑轴力减小越显著.注浆会引发更深处支撑轴力增大,需引起关注.
5)对于类似工程,在隧道侧方进行竖直注浆时,随着注浆位置逐渐下移,隧道椭圆度恢复率先增大后减小.隧道处于隆起区和过渡区,竖向注浆体中心水平线高于隧道中心水平线1 m左右时,隧道椭圆度恢复率达到最佳;隧道处于沉降区时,注浆体与隧道中心水平线平齐时,隧道椭圆度恢复率最佳.
