动车组转臂节点刚度特性及疲劳寿命研究

2023-01-18侯茂锐李永华陈秉智白肖宁胡晓依

北京交通大学学报 2022年6期

侯茂锐，李永华，陈秉智，白肖宁，胡晓依

（1.中国铁道科学研究院集团有限公司铁道科学技术研究发展中心，北京 100081；2.大连交通大学机械工程学院，辽宁大连 116028）

转臂节点因结构简单，各向刚度相互独立，被广泛应用于动车组轴箱定位系统.其结构主要由芯轴、橡胶层和轴套组成，橡胶材料具有优良的隔振和缓冲性能，所以转臂节点可有效减小因线路不平顺、钢轨磨耗以及车轮多边形等原因引起的振动和冲击，从而提高车辆运行的平稳性和舒适性［1］.

转臂节点对车辆的运行品质有着重大影响，一旦发生故障将危及行车安全，众多学者对其展开相关研究.陆海英［2］依据结构特点对现有轴箱定位装置进行了分类.张益瑞等［3］提出一种基于转向架试验台的刚度试验方法，为转臂节点及其他轨道车辆橡胶元件刚度测试提供了参考.卢翀等［4］利用有限元软件计算了动车组轴箱转臂节点的刚度特性，对比分析了基于Mooney-Rivlin与Ogden这两种橡胶本构模型的计算结果与试验结果.一些学者研究了转臂节点刚度特性对车辆系统动力学性能的影响.邹波等［5］设计出一种具有变刚度特性的新型轴箱转臂节点，并进行动、静态刚度试验以验证结构设计方案的合理性.张隶新等［6］基于Poynting-Thomson模型研究激扰频率和幅值对转臂节点动态刚度的影响，分析变刚度转臂节点的车辆动力学性能.祁亚运等［7］分析了变刚度转臂节点的频变特性和幅变特性，并研究变刚度转臂节点对车轮磨耗的影响.刘诗慧等［8］实现了转臂节点结构尺寸相关性和动态非线性动力学建模.侯茂锐等［9］结合动力学仿真和试验研究得到刚度分布特征，并探究转臂节点刚度变化对车辆动力学性能的影响.此外，部分学者重点研究了转臂节点刚度的温变特性［10-11］.转臂节点工作环境恶劣且承载情况复杂，在车辆运行过程中橡胶层容易产生疲劳失效，因此研究其疲劳寿命具有重要意义.Andriyana等［12］通过试验观察到循环载荷下橡胶材料中存在微观缺陷，以此构建橡胶疲劳寿命预测模型.Zine等［13］研究了多轴载荷下橡胶材料的疲劳寿命.王文涛等［14-15］提出张量形式的疲劳寿命计算公式，用最小二乘法拟合出疲劳寿命函数预测模型.上官文斌等［16］以不同损伤参量建立橡胶疲劳寿命预测模型.丁智平等［17］基于连续损伤模型探讨了橡胶材料的疲劳寿命研究方法.以上研究大多基于仿真分析或疲劳试验，并未考虑振动载荷的影响以及转臂节点轴向、径向刚度的差异性.

本文对服役120万km的转臂节点进行刚度测试，得到其刚度分布特征，考虑本构模型和随机载荷的影响，利用有限元法研究径向、轴向刚度随载荷的变化规律，计算分析不同载荷下转臂节点的疲劳寿命.

1 转臂节点结构及橡胶本构模型

1.1 转臂节点结构

转臂节点结构如图1所示，其主要作用是连接轮对与转向架构架，约束二者之间的相对运动并传递牵引与制动力.安装、更换转臂节点必须落下轮对，然后进行压装等一系列操作，流程复杂且耗时较长.一旦装车使用，在正常服役期限内一般不会拆卸，因此无法得知服役过程中转臂节点刚度，需要对其刚度展开系统性研究.

图1 转臂节点几何模型Fig.1 Geometric model for axle box rubber joint

橡胶层可以提供转臂节点不同的径向和轴向刚度，以满足车辆对一系定位的要求.CRH3型动车组转臂节点名义轴向刚度为12.5 MN/m，径向刚度为120 MN/m，标准规定刚度在“名义刚度×（1±15%）”范围内允许装车使用［9］.

1.2 橡胶材料本构模型

目前橡胶材料力学性能主要有两种描述方法：基于现象学的描述，该方法认为橡胶是连续介质，用单位体积应变能密度描述橡胶材料特性；基于热力学统计方法的描述，该方法认为橡胶弹性恢复力来自橡胶伸长时结构由高度无序变为有序过程中熵的减少［18］.

普遍认为橡胶材料是各向同性、不可压缩的超弹性材料，其应变能可分解为应变偏量和体积应变能两种，即

式中：f为橡胶材料变形张量函数；g为橡胶材料体积压缩比函数，令进行泰勒展开，则式（1）可转化为完整的多项式应变能密度函数

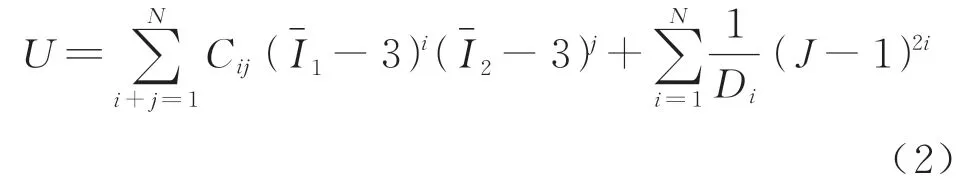
式中：Cij为泰勒展开式系数；N为多项式阶数；i=为变形张量；J为体积压

缩比；Di为材料压缩比，若其等于0，则说明材料完全不可压缩.

如果N等于1，表示只保存线性部分应变偏量，即为Mooney-Rivlin模型

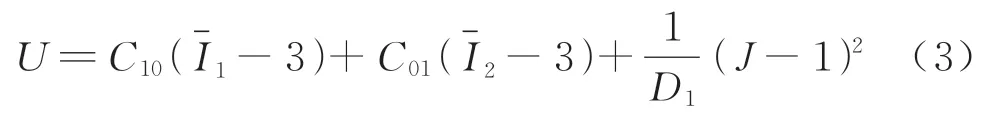
式中：C10和C01为橡胶材料参数，通过拟合试验数据得到；D1为材料压缩比.

在没有实测试验数据时采用Mooney-Rivlin模型，能够精确描述出橡胶材料在小应变或中等应变下的变形问题，但如果发生大变形，Mooney-Rivlin模型存在较大误差，无法准确表征橡胶材料应力应变关系，此时应选取其他本构模型.

Ogden模型以橡胶材料伸长率作为自变量，不仅可以很好地表征出橡胶材料小变形问题，大变形问题也有良好的精度.其应变能形式为

式中：λ1、λ2和λ3为橡胶材料伸长率；N为Ogden模型阶数，阶数越高，模型的拟合精度越高；αi、μi为材料系数.

依据单轴、双轴拉伸试验数据拟合Mooney-Rivlin和Ogden本构模型，对比在相同试验数据下两种本构模型之间的精度差异，以选取合适的橡胶本构模型，拟合结果如图2所示.

由图2（a）可知，Mooney-Rivlin模型与Ogden模型在小变形条件下的拟合结果均与单轴拉伸试验数据较为贴合，但发生大变形时，Ogden模型拟合结果较符合试验数据的趋势走向，而Mooney-Rivlin模型则存在较大偏差.由图2（b）可知，双轴拉伸试验数据拟合后，Mooney-Rivlin模型的拟合曲线与试验数据始终存在小范围误差，Ogden模型较Mooney-Rivlin模型的拟合效果更佳.综上，本文选取Ogden本构模型表征橡胶材料属性，以建立精确的转臂节点有限元模型.

图2 不同本构模型拟合结果Fig.2 Fitting results of different constitutive models

2 转臂节点非线性有限元分析

2.1 转臂节点有限元模型

进行有限元分析时，在保证计算结果的前提下可对几何模型简化处理，以减少计算时间，提升分析效率.转臂节点几何结构左右对称，建立有限元模型时可采用二分之一结构，并忽略细小的倒角及芯轴两端的螺纹孔等不影响分析结果的几何特征.

将几何模型进行网格划分，划分好的网格模型导入有限元软件中定义材料参数、网格类型、边界条件等.设置芯轴和轴套材料泊松比为0.3，弹性模量为206 000 Mpa，橡胶材料参数按照式（4）进行设置，Ogden模型中的橡胶材料参数分别为：μ1=1.33×10-4，α1=12.56，μ2=1，α2=1.金属网格单元类型设置为八节点六面体线性缩减积分单元C3D8R，橡胶层网格单元类型设置为八节点六面体杂交单元C3D8H，转臂节点有限元模型如图3所示.考虑转臂节点实际承载情况，对有限元模型分别施加径向、轴向载荷.首先沿O-xz平面施加对称约束（模型的对称面），径向加载时约束芯轴两端的安装平面，轴向加载时约束轴套一侧端面，具体的边界条件及载荷设置见表1.

表1 载荷边界条件Tab.1 Load boundary conditions

图3 转臂节点有限元模型Fig.3 Finite element model of axle box rubber joint

2.2 非线性有限元分析

分别对不同载荷工况下的转臂节点有限元模型进行求解.当径向、横向加载50 kN时，所产生的应力、应变及相对位移最大，最能体现转臂节点结构强度需要反映的问题，此处仅给出50 kN载荷下转臂节点分析结果，如图4和图5所示.

图4 径向结果Fig.4 Analysis results under radial load

图5 轴向结果Fig.5 Analysis results under axial load

随着载荷的增大，转臂节点的应力、应变和位移逐渐增大.由图4可知，径向加载时，最大应力出现在芯轴安装平面处，此处结构突变且为主要承载区域，所以容易产生应力集中；应变最大位置在橡胶层与芯轴和轴套连接部位，最大位移发生在橡胶层两端面Z轴负方向的受压侧，造成此现象的原因是受径向载荷挤压，芯轴与轴套间的内部空间被压缩，橡胶层向两端空间自由处发生变形，相对变形较大.由图5可知，轴向加载时应力主要集中在芯轴阶梯区域，因为芯轴受载向X轴正方向移动，X轴负方向阶梯处的橡胶受压，处于“挤压”状态，正方向阶梯处橡胶为“放松”状态，故X轴负方向阶梯区域应力较大；芯轴位移量最大，与之相连的橡胶层内表面位移也最大，应变也最大.根据工程经验可知，转臂节点容易在上述部位产生开裂或出现疲劳裂纹，说明有限元分析结果符合工程实际.

3 转臂节点刚度特性

转臂节点刚度对车辆蛇行稳定性、曲线通过性能有重要影响［9］.传统设计往往通过理论计算获得理想化的转臂节点刚度，但最终结果与实际情况存在一定偏颇.为弥补理论计算的不足，将仿真分析和试验研究相结合，探究刚度随载荷变化规律及服役转臂节点的刚度分布特征.考虑到实际服役过程中，转臂节点受到的载荷工况复杂，因此，仿真分析分别计算了载荷在10～50 kN范围变化对转臂节点静刚度的影响.

3.1 计算结果

已知刚度是结构受载时抵抗变形的能力，其大小等于载荷与位移的比值，即

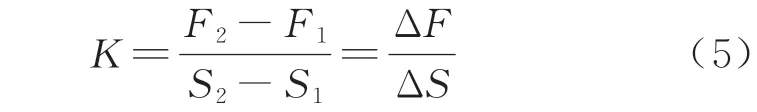
式中：K为结构刚度值；Fi为所承受的载荷；Si为在载荷Fi作用下产生的变形量；ΔF和ΔS分别为刚度值和载荷的变化值.

提取非线性分析所得到的相对位移，结合式（5）分别计算出转臂节点在径向、轴向不同载荷下的刚度，如图6所示.

由图6可知，转臂节点径向刚度、轴向刚度最大值分别为111.11 MN/m、13.98 MN/m，且两方向的刚度值分别在104～112 MN/m、13.80～14.00 MN/m范围内波动，均满足标准要求.图6（a）显示径向刚度随载荷增大呈波动下降趋势，虽在一定范围内有波动，但波动幅值逐级减小，趋于稳定.由图6（b）可知，轴向刚度整体也呈下降趋势，且波动幅值相对径向刚度较小，但波动频率较大且存在随机性.总体而言，转臂节点径向、轴向刚度随载荷增大呈现非线性的减小趋势，主要由于橡胶材料的强非线性特性引起.

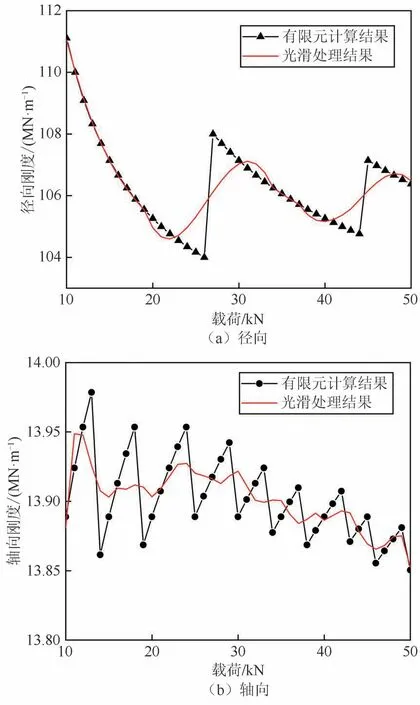
图6 刚度随载荷的变化规律Fig.6 Changing law of stiffness with load

3.2 试验结果

对154个服役120万km的转臂节点进行刚度测试，如图7所示.测试径向刚度时，以1 mm/min的速度从0加载至100 N，弥补测试部件与转臂节点之间的间隙，然后加载至130 kN，再以同样速度卸载至100 N，循环3次，记录第3次载荷-位移曲线，取10～100 kN的载荷-位移计算径向刚度.轴向刚度测试与径向步骤相同，不同之处在于试验载荷由130 kN调整至22 kN，取3～14 kN的载荷-位移曲线计算.对刚度测试结果进行统计分析，得到刚度分布特征如图8所示.

图7 刚度测试Fig.7 Stiffness test

由图8可知，转臂节点径向刚度分布范围在95～145 MN/m之间，频率最大区间为95～110 MN/m之间，即表明处于此刚度范围内的转臂节点数量较多.忽略截尾特征，径向刚度近似服从正态分布，针对此分布进行假设检验

图8 刚度分布特征Fig.8 Stiffness distribution characteristcs

式中：F(x)为服役120万km后转臂节点径向刚度分布函数；H0和H1为两种假设，其中所给定的正态分布参数μ，σ2均未知，用极大似然估计法估算其值

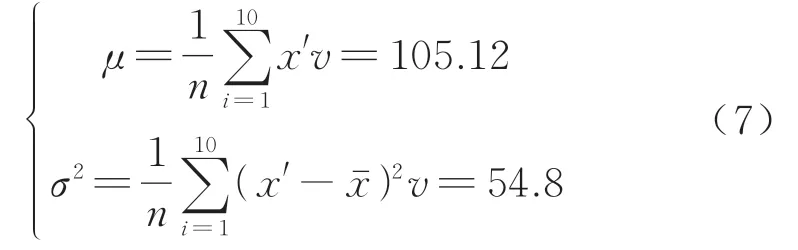
式中：x′为服役120万km后转臂节点的径向刚度，即为变量；xˉ为变量均值；n为变量个数；v为假设检验参数值，可通过经验取值确定.

则假设H0可写成H0：F(x)∈{N(105.12，7.42}，计算出统计量χ2的值为9.57，经检验可知

故在显著水平0.005下接受H0，即认为径向刚度服从N（105.12，7.42）正态分布.

轴向刚度分布范围在10～16 MN/m之间，频率最大区间为11～14 MN/m之内，经假设检验轴向刚度服从N（12.95，1.75）正态分布.

对比有限元计算与试验结果，仿真计算得到的转臂节点径向刚度分布在104～112 MN/m之间，轴向刚度分布在13～14 MN/m之间，均在试验结果范围内，与试验结果对应较好，验证了转臂节点有限元模型的可靠性.

4 转臂节点疲劳寿命分析

与芯轴和轴套相比，橡胶层更容易出现疲劳损伤.橡胶材料具有超弹性特性，在外部载荷作用下通常会发生大变形，这一点不同于金属材料，因此不宜用Mises应力评估其疲劳性能，而且转臂节点承载情况复杂，采用主应力法结合橡胶材料S-N曲线可对疲劳寿命进行准确评估［12］.

转臂节点受力状态可用3个方向的主应力表示，并以此作为疲劳寿命计算的损伤参量.已知

式中：σf为3个主应力的等效应力；σi(i=1，2，3)为3个方向主应力；A，B为主应力系数，当σ2，σ3＞0时，A=B=1，当σ3≤σ2≤0时，A=B=0.

根据疲劳载荷工况，对有限元模型施加周期循环载荷，提取主应力值结合橡胶材料S-N曲线［19］，如图9所示，分别计算转臂节点径向受载和轴向受载条件下的疲劳寿命，疲劳寿命云图分布如图10和图11所示.

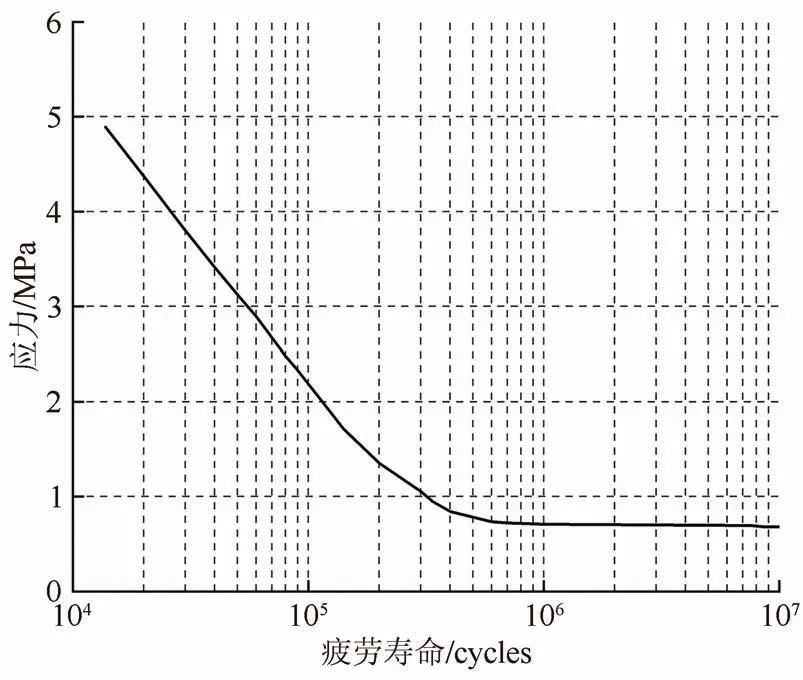
图9 橡胶材料S-N曲线Fig.9 S-N curves of rubber material

由图10可知，径向加载时，橡胶层疲劳损伤最先出现在Z轴负方向阶梯区域，随着载荷增大，疲劳损伤区域逐渐扩大，疲劳寿命也逐渐降低.Z轴负方向疲劳寿命总体低于正方向，这是加载方向所导致的.此外，橡胶层内外表面的疲劳寿命较低，结合图4可知此处应变较大，故疲劳寿命相对较低.由图11可知，加载10 kN时为无限寿命，疲劳损伤最早出现在X轴正方向橡胶层内表面阶梯处的部分区域，并逐渐扩大.随着载荷增大，疲劳损伤区域逐渐扩大，疲劳寿命也逐渐降低，受载一侧的疲劳寿命低于未受载侧.由疲劳寿命分析结果可知，转臂节点径向载荷下疲劳寿命低于轴向载荷疲劳寿命，主要因为径向受载的应力应变较大.转臂节点一般承受载荷在10～20 kN范围内，此时转臂节点疲劳寿命约为2 398 833次；对于50 kN的极限载荷，疲劳寿命约为1 148 154次，满足工程应用要求.