基于北京大兴机场线刚性接触网线路的受电弓适应性研究
2023-01-18郗汭李波赵志远袁骞
郗汭,李波,赵志远,袁骞
(北京中车赛德铁道电气科技有限公司,北京 100176)①
北京大兴机场线为国内首条时速为160 km的刚性接触网线路,是包含刚性网段、柔性接触网段及刚柔过渡段的综合接触网线路[1].弓网系统的状态直接关系到电气列车的运行性能、安全性以及乘坐舒适性,而作为弓网系统的重要部件,受电弓工作环境随列车运行速度的提高而趋于恶劣[2].因此受电弓与接触网的动态相互作用研究即适应性研究是列车运行平稳性与安全性评估分析的重要组成部分[3].
当前对于弓网系统的性能研究多着重于接触网性能的提升,张宗芳等[4]提出了一种适用于隧道内部的新型刚柔结合接触网结构,相比其他类型接触网该接触网在结构高度、弹性均匀度等指标上进行优化;关金发等[5]针对刚柔过渡结构进行仿真分析,提出了满足双弓160 km/h的设计方案.在弓网系统多种类型的接触网中,刚性接触网占用空间小、结构简单、安全可靠,已大量投入城市地铁轻轨的线路中.唐志强等[6]设计了一种硅橡胶材质的接触线,可提升耐磨性和检修质量;代洪宇[7]提出了200 km/h交流刚性接触网方案,提升受电弓碳滑板的磨耗均匀度.针对受流装置的性能研究大多集中在与接触线的耦合关系上,梅桂明[8]研究刚性接触网与滑板异常磨耗的机理,以及弓网系统参数对滑板磨耗的影响;吕阶军[9]针对提高受电弓运行稳定性和可靠性,提出一种弓头、弓角等悬挂构建的改进方案.
为了对弓网系统进行动态受力和动力学分析,本文在已设计完毕的北京大兴机场线[10]的基础上对DSA250型和DSA380型受电弓进行数值仿真计算.由于受电弓在柔性悬挂接触网系统下运行状态较好,因此针对刚性接触网和刚柔耦合过渡段对受电弓进行适应性分析.
1 评价标准
表征弓网动态特性的主要技术指标是弓网接触力[11],根据标准EN 50367:2012[12],接触力标准偏差σ应满足
σmax<0.3Fm
(1)
式中:σmax为最高速度时的接触力标准偏差;Fm为接触力平均值.
根据标准EN 50119:2009[13],交流系统的最大与最小接触力应满足以下条件:
最大接触力:
Fmax<300 N,(V≤200 km/h)
Fmax<350 N,
(200 km/h (2) 最小接触力: Fmin>0 N (3) 本文采用数值仿真方式对弓网动态相互作用进行研究分析,弓网仿真模型由受电弓模型、接触网模型、弓网接触模型组成[14]. 受电弓和接触网模型采用Ansys单元库内单元进行建模:受电弓模型主要由三质量块模型构成,采用质点Mass21和线弹簧阻尼单元Combine14创建,在最下方质量块施加抬升力;接触网模型采用梁单元Beam4单元创建,吊弦采用Combine39非线性弹簧单元创建,以模拟接触网吊弦的松弛效应;刚性接触网的支撑采用壳单元等建模,连接处采用MPC单元模拟铰接连接;刚柔过渡处的汇流排则采用变截面梁单元模拟汇流排的截面变化;接触网的支撑采用固定约束,考虑自重作用;受电弓模型与接触网通过接触单元耦合,接触刚度参考EN 50318:2018[15]设置. 以DSA250和DSA380两种受电弓作为计算模型,设置受电弓为三质量块模型,接触网高为5 300 mm.受电弓三质量块模型示意图见图1.图中:m为质量、k为刚度、c为阻尼、F为静态力. 图1 受电弓三质量块模型 受电弓系统采用三质量块模型可以很好地反映弓网间动态接触力的关系,但模型特点无法体现开闭口区别,因此不考虑开闭口工况影响. 北京大兴机场线刚性接触网段的典型锚段参数如下:锚段长度为499.8 m;拉出值为±220 mm;标准跨距为8 m;布置方式为三折线布置;锚段关节长度为6 m;汇流排终端长度为5.95 m;单根汇流排长度为12 m;汇流排终端悬臂长度为1.5 m;汇流排终端翘起段长度为1 m;汇流排终端翘起高度为70 mm. 北京大兴机场线悬挂方案采用多维度可调节腕臂装置,装置示意图见图2.该装置依据接触网系统几何参数的多维度定位需求进行研发设计,成功实现了水平腕臂在曲线超高地段竖直方向的连续调节,进一步提升了弓网匹配性能. 图2 多维度可调节腕臂 根据平面布置方案及悬挂方案搭建接触网有限元模型,刚性接触网段和刚柔过渡段接触网有限元模型见图3. (a) 刚性接触网 基于Ansys有限元动力学分析,通过接触单元将接触网和受电弓直接耦合起来得到弓网系统的整体模型,进而构建弓网耦合系统的动力学平衡方程.弓网接触模型采用直接耦合法,将受电弓弓头位移与接触线接触点位移耦合.因为弓网接触力主要通过垂向的相对位移来体现,故模型主要考虑垂向耦合[16],并且为正确考虑受电弓高速滑动时纵向冲击造成的接触力变化,纵向接触力采用相同形式的计算方法,垂向接触力和纵向接触力的表达式为: (4) (5) 图4 弓网接触模型 系统动力学平衡方程的矩阵形式为: (6) 在弓网系统中,受电弓采用三质量块模型进行分析,其动力学平衡方程表达式为: (7) 式中:mi、ki、ci(i=1,2,3)为质量、刚度、阻尼;F0为受电弓静态接触力. 将式(4)、式(5)代入动力学平衡方程式(7),并采用直接积分法对弓网动态接触力进行求解[17]. 以北京新机场线刚性接触网和刚柔过渡为基础,对DSA250和DSA380两种受电弓参数在160 km/h、180 km/h 、200 km/h、220 km/h速度等级下,静态抬升力为70 N和80 N时的弓网动态特性进行研究,仿真工况见表1. 表1 受电弓动态特性仿真工况 以表1数值分析工况为主进行弓网动态特性仿真,由仿真结果可得,DSA250及DSA380型受电弓均能满足列车160~220 km/h的行驶要求,接触力标准偏差符合要求,最大、最小接触力符合标准范围要求,刚性接触网条件下受电弓动态特性仿真结果见表2,运行速度分别为200 km/h、220 km/h的弓网动态接触力见图5. 表2 刚性接触网条件下受电弓动态特性仿真结果 N (a) 200 km/h 从图中可以看出,DSA250型与DSA380型受电弓标准差变化趋势相同,均随速度等级提高而增大;同时接触力最大值与最小值也呈相同变化趋势.在不同速度等级条件下,DSA380型受电弓的接触力标准差均小于DSA250型. 柔性接触网段过渡至刚性接触网段条件下DSA250型受电弓与DSA380型受电弓的动态接触力见图6. (a) 160 km/h图6 刚柔过渡条件下的弓网动态接触力 (b) 180 km/h DSA250型受电弓与DSA380型受电弓由柔性接触网段过渡至刚性接触网段时,当运行速度不高于180 km/h,弓网接触力处于标准范围内且数据表现良好;当运行速度不低于200km/h,虽然弓网接触力仍符合式(2)、式(3)的标准要求,但已经接近标准限制,数据表现一般.两种型号受电弓的静态抬升力均随速度的增加而增大,同时接触力标准差也呈相同变化趋势.对标准差及0.3×Fm-σ数据结果进行分析,DSA380型受电弓在此类工况下的动态特性优于DSA250型受电弓. 根据四种运行速度条件下的弓网动态接触力可知:同等运行速度下两种类型受电弓与接触网的动态接触力变化趋势接近,动态接触力均符合标准要求. 刚性接触网段过渡至柔性接触网段条件下DSA250型受电弓与DSA380型受电弓的动态仿真结果见表3. 表3 刚柔过渡条件下受电弓性能仿真结果 N DSA250型及DSA380型受电弓在由刚性接触网段过渡至柔性接触网段的所有仿真速度等级下,弓网接触力全部处于标准要求范围内,且标准差小于由柔性接触网段过渡至刚性接触网段时,最小接触力也相对较大,离网风险小,可见弓网性能优于柔性至刚性过渡的工况. (1)DSA250型及DSA380型受电弓在160~220 km/h速度等级下,接触力分布整体趋势相同,均能满足弓网受流要求,其中DSA380型受电弓动态特性较优. (2)在刚性接触网条件下,受电弓以较低速度运行时,弓网动态接触力相对平稳,整体波动较小,仅在锚段关节处发生波动;随着速度等级的提高,接触力波动明显增大,标准差也随之增大;当速度增加至220 km/h时,接触力分布更加分散,仿真结果在标准要求范围内. (3)受电弓在刚柔过渡处运行时,弓网接触力变化较大:从柔性网段过渡到刚性网段运行时变化更加明显,当速度超过180 km/h,最小接触力接近0 N;从刚性网段过渡到柔性网段时,接触力均处于标准范围内,且接触力标准差比受电弓从柔性接触网段过渡至刚性接触网段时小,弓网系统性能更好. (4)DSA250型受电弓与DSA380型受电弓均能满足列车在北京大兴机场线以160~220 km/h速度行驶的要求,弓网接触力与接触力标准差均符合要求,无离线现象.但是当受电弓从柔性接触网段过渡到刚性接触网段时,弓网接触力变化较大,应降速运行,从而获取更优的弓网受流性能.2 弓网系统有限元模型
2.1 受电弓模型

2.2 接触网模型


2.3 弓网接触模型


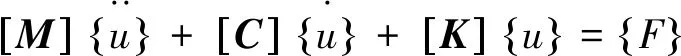
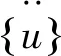
3 数值仿真分析工况及计算结果
3.1 数值仿真分析工况

3.2 刚性接触网条件下仿真计算结果


3.3 刚柔过渡条件下仿真计算结果(柔→刚)
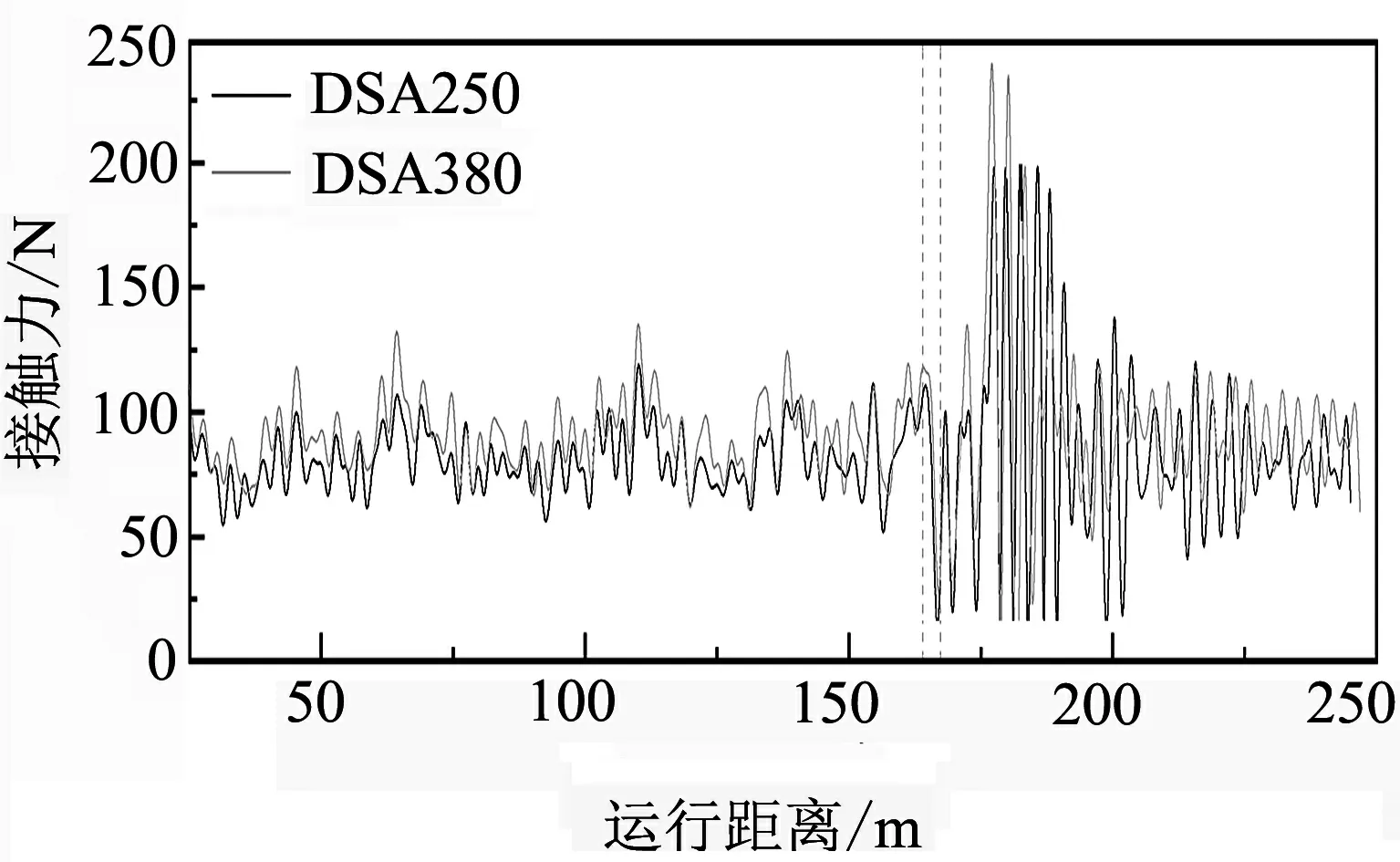

3.4 刚柔过渡条件下仿真计算结果(刚→柔)

4 结论
