现行标准对《04通规》设计桥梁可靠度的影响分析
2023-01-18梁茜雪李增科周亭林
梁茜雪 李增科 周亭林
(广西交科集团有限公司 南宁 530007)
0 引 言
为适应公路交通需求,2015年实施的JTG D60—2015《公路桥涵设计通用规范》(以下称为《15通规》)替代了已使用11年的JTG D60—2004《公路桥涵设计通用规范》(以下称为《04通规》).《15通规》结合交通部西部交通建设科技项目“桥梁设计荷载与安全鉴定荷载的研究”对全国汽车荷载现状调查和统计分析的成果,考虑到当前超载问题无法回避的现状,通过适当提高中小跨径桥梁的安全储备,以提高此类桥梁抵御超载的能力[1].该标准通过调整汽车荷载等级和相关系数,使设计荷载与实际运营荷载最大程度契合,从设计上保障了桥梁安全.由于当前经济水平的制约,多数按《04通规》设计的在役桥梁仍维持原设计荷载继续运营,荷载水平与实际承载能力的差距加快了结构的损伤和劣化,因此有必要研究现行汽车荷载标准下原设计标准桥梁的可靠性.目前,国内较多学者着眼于研究《15通规》与《04通规》汽车荷载效应的比较[3-5],少数依据设计规范验算旧桥施加新标准荷载后的富余量[6],尚无以可靠度为标准分析按《04通规》设计桥梁在《15通规》下安全性的研究.
JTG 2120—2020《公路工程结构可靠性设计统一标准》定义当前公路工程结构、构件主要设计方法为“以概率理论为基础、以分项系数表达的极限状态设计方法”[7].概率极限状态设计表达式中取用的各分项系数是根据极限状态方程中各基本变量的有关统计参数及概率分布类型和规定的目标可靠指标,通过可靠度分析计算,按优化方法,并考虑工程经验确定的.分项系数的优化原则为使极限状态设计表达式下的结构可靠指标与目标可靠指标误差最小,因此该方法不是直接的可靠度设计方法,在极限状态设计表达式下的结构可靠指标并不等于目标可靠指标,由此计算出的桥梁承载能力与设计可靠度要求存在偏差.鉴于此原因,为准确评估按《04通规》设计桥梁在《15通规》要求下的安全性,揭示结构在提载前后可靠度的变化,评价加固需求程度,本文以抗力、恒载效应、汽车荷载效应为基本随机变量,采用工程可靠度理论分析桥梁结构在不同荷载标准下的可靠度水平,指导养护维修决策.
1 《15通规》较《04通规》汽车荷载的主要变化
1) 结构重要性系数 《15通规》中各设计安全等级对应的桥梁结构有了明显变化,将原为二级的“中桥”和“重要小桥”均升级为一级,原为三级的“小桥”升级为二级.对应的结构重要性系数γ0分别由1.0增至1.1、由0.9增至1.0.
2) 汽车荷载等级 将二级公路桥梁设计汽车荷载等级由公路-Ⅱ级调整为公路-Ⅰ级,仅当二级公路作为集散公路且交通量小、重型车辆少时,可采用公路-Ⅱ级;取消了《04通规》中对四级公路在重型车辆少时的折减.
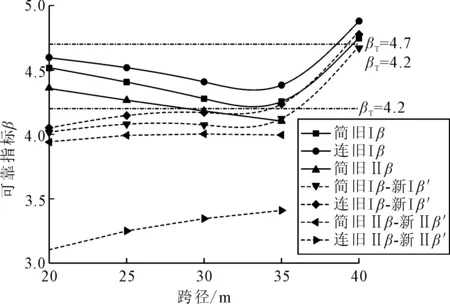
3) 车道荷载 车道荷载仍由均布荷载和集中荷载组成.公路-Ⅰ级均布荷载qk取10 kN/m与原标准相同,但集中荷载Pk在桥梁计算跨径L0≤5 m时由180 kN调整至270 kN,在5 m 4) 横向车道布载系数(原为“车道横向分布系数”) 课题组在与国内外对比的基础上进行多车道重车相遇概率研究,《04通规》的多车道折减系数取值适用于当前及今后一个时间内的交通状况,因此仍维持原规范系数,但单车道系数借鉴国外经验由1.0提高至1.2. 在仅考虑恒载和汽车荷载基本组合时,桥梁结构构件的抗力、恒载效应和汽车荷载效应为基本随机变量,结构功能函数表示为[8] Z=g(R,SG,SQ)=R-SG-SQ (1) 式中:R、SG和SQ为抗力、恒载效应和汽车荷载效应的随机变量;Z或g(·)为结构功能函数. 由式(1)和文献[8-9]理论建立失效概率方程为 Pf=P(Z≤0)= (2) 式中:fR(r)、fSG(sG)、fSQ(sQ)分别为抗力R、恒载效应SG和汽车荷载效应SQ的概率密度函数. 根据《04通规》构件承载能力极限状态表达式,抗力标准值与作用效应组合设计值的关系为 Rk=γ0γR(γGSGk+γQSQk) (3) 式中:Rk、SGk和SQk分别为抗力、恒载效应和汽车荷载效应的标准值;γG和γQ分别为恒载效应和汽车荷载效应分项系数;γR为抗力分项系数. 依据文献[9],抗力、恒载效应和汽车荷载效应分别服从对数正态、正态和极值Ⅰ型分布,各基本变量的统计参数由抗力、恒载效应和汽车荷载效应标准值为 (4) 式中:μR、σR、δR分别为抗力R的均值、方差和变异系数;μSG、σSG、δSG分别为恒载效应SG的均值、方差和变异系数;μSQ、σSQ、δSQ分别为汽车荷载效应SQ的均值、方差和变异系数;kR、kSG、kSQ和δR、δSG、δSQ为R、SG和SQ的平均值与标准值的比值;kR、kSG、kSQ和δR、δSG、δSQ取值均按文献[12]查取. 与可靠性对应的完成的概率称为结构可靠度.结构可靠度可以用失效概率Pf或可靠指标β表示,两者的关系为 β=-Φ-1(Pf) (5) 式中:Φ-1(·)为标准正态分布函数的反函数. 本文采用验算点法计算可靠指标,具体计算流程见图1. 图1 验算点法计算可靠指标流程图 依据图1计算桥梁在原设计汽车荷载下的设计可靠指标β,此时的抗力标准值Rk取等于恒载效应和汽车荷载效应组合值的理想抗力.本文引入抗力富余需求系数λ,该系数为一无量纲参数,可直观反映现标准要求抗力与原设计理想抗力的关系,且已计入目标可靠指标影响,可用于安全等级不同桥梁间加固需求比较. (6) 计算对象包括通用图中按《04通规》公路-Ⅰ级汽车荷载设计的20~40 m简支和连续正交T梁桥(单幅桥面宽13.5 m)和按公路-Ⅱ级汽车荷载设计的20~35 m简支正交T梁桥(单幅桥面宽13.5 m),其中连续梁桥按三跨等跨布置.采用“梁格法”建立有限元模型,按《04通规》和《15通规》施加单车道、双车道和三车道汽车荷载,计算T梁最大恒载效应标准值和最大汽车荷载效应标准值.各跨径边梁和中梁作用效应弯矩计算结果分别见表1~2,表中“旧Ⅰ”“旧Ⅱ”分别对应《04通规》的公路-Ⅰ级和公路-Ⅱ级,“新Ⅰ”“新Ⅱ”分别对应15通规的公路-Ⅰ级和公路-Ⅱ级. 表1 边梁弯矩恒载效应和汽车荷载效应标准值计算结果表 表2 中梁弯矩恒载效应和汽车荷载效应标准值计算结果表 因边梁和中梁趋势相同,本文仅建立边梁提载后跨径与荷载效应标准值增长率关系曲线(见图2),荷载效应分别取汽车荷载效应和恒载与汽车荷载组合效应两种. 由图2可知: 1) 汽车荷载效应和恒载与汽车荷载组合效应标准值增加率均随跨径增大而减小,汽车荷载效应下降速率较组合效应快.汽车荷载效应占总效应的比例随跨径增大而减小,对组合效应增长率的影响减小,因此组合效应随跨径下降速率较汽车荷载效应慢. 2) 在提载时,如汽车荷载等级不变,则相同跨径T梁桥的汽车荷载标准值和恒载与汽车荷载组合效应标准值增长率均非常接近. 3) T梁桥由《04通规》的公路-Ⅱ级提高至15通规的公路-Ⅰ时,汽车荷载标准值或恒载与汽车荷载组合效应标准值增长率较同级提载明显上升. 单孔跨径为20~35和40 m桥梁分别属于中桥和大桥,在《04通规》中对应安全等级为二级和一级,故原目标可靠指标为4.2和4.7[10].因15通规将中桥的安全等级提升为一级,所以单孔跨径为20~35 m桥梁的目标可靠指标提高到4.7. 图3为T梁桥边梁提载前后桥梁可靠指标与跨径的关系曲线,为方便观察,增加提载前后的βT横线. 图3 预应力混凝土T梁桥边梁跨径与可靠指标关系曲线图 由图3可知: 1) 按《04通规》计算的跨径20,25,30,35 m的T梁桥可靠指标β均大于或接近原目标可靠指标4.2,单孔跨径40 m的T梁桥β略高于原目标可靠指标4.7. 3) 提载后,40 m跨径桥可靠指标β′基本满足目标可靠指标4.7;其余跨径桥梁因目标可靠指标提高及荷载效应增大的双重影响下,可靠指标β′明显低于目标可靠指标4.7,范围在3.104~4.235. 4) 跨径越小的桥梁活载效应与恒载效应比值越大,即活恒效应比越大.因可靠指标与活恒效应比成正比,故跨径越小原可靠指标β越大;而荷载效应增长率则相反,跨径越小增长率越大,造成可靠指标下降越多.在以上两个效果相反因素共同作用下,出现了同级提载时,具有相同原目标可靠指标的20,25,30,35 m的T梁桥的β′均很接近的情况,因此虽然按《04通规》设计的中桥在15通规下跨径越小汽车荷载效应越大,但不同跨径桥梁的可靠度和安全性是相近的. 以2.4的方法试算出提载至15通规相应汽车荷载等级时的抗力富余需求系数,见表3. 表3 预应力混凝土T梁桥边梁抗力富余需求系数计算结果表 为分析目标可靠指标提高对可靠度的影响,表3中除提供对应《15通规》要求目标可靠指标的富余需求系数λ2外,还计算未提高时的富余需求系数λ1.从表3中数据看,如仍沿用原目标可靠指标,除跨级提载外,各跨径桥梁的抗力富余需求系数小于1.0或仅略大于1.0,仍能满足要求.按《15通规》要求,除跨径40 mT梁仍使用原目标可靠指标4.7外,其余跨径均由4.2增至4.7,此时20~35 m跨径的同级提载桥梁抗力富余需求系数均在1.1附近.显然,目标可靠指标的提高大幅增加了结构抗力需求,富余需求系数约提高0.1.因用于计算可靠指标的抗力为理想抗力,实际设计抗力总是保证一定富余,通常不小于10%,所以在不考虑运营期抗力衰减情况下,同级提载的桥梁仍能达到目标可靠指标.但从《04通规》的公路-Ⅱ级提高至《15通规》的公路-Ⅰ级时,λ2已超过1.2,必须提高桥梁抗力水平才能满足要求. 1) 《15通规》主要通过调整车道荷载受力图示的集中力、提高安全等级和提高汽车荷载等级三个方面达到增加中小跨径桥梁安全储备的目的.单孔跨径小于40 m(不含40 m)的跨级提载桥梁可靠指标很难满足《15通规》要求,应作为首要检测评估承载能力桥梁,并依据结果及时加固或重建. 2) 《15通规》虽然提高了中小跨径桥梁承载能力要求,但按《04通规》相同汽车荷载等级设计的中桥可靠指标基本能达到要求.桥梁管养单位应结合桥梁运营状况和结构劣化程度,选择性地对该类桥梁进行承载能力评估和维修加固处置. 3) 采用含分项系数的设计表达式计算旧桥承载能力方法具有实用简便的优点,但也存在可靠指标与目标可靠指标不一致情况,在对桥梁安全状况评估有精确要求时,宜直接计算结构可靠指标或失效概率,获取准确数据.2 研究方法
2.1 结构功能函数和失效概率方程
2.2 基本随机变量统计参数
2.3 可靠指标计算方法
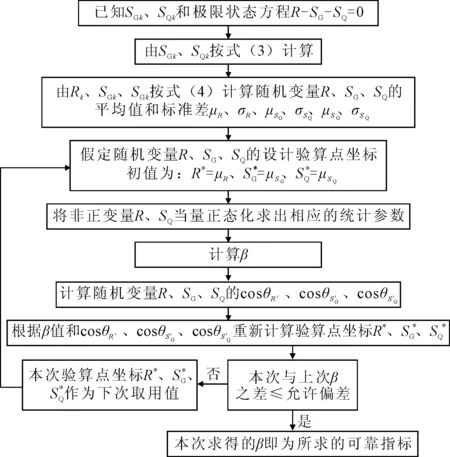
2.4 抗力富余需求系数λ
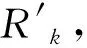
3 预应力T梁桥可靠度研究
3.1 荷载效应计算
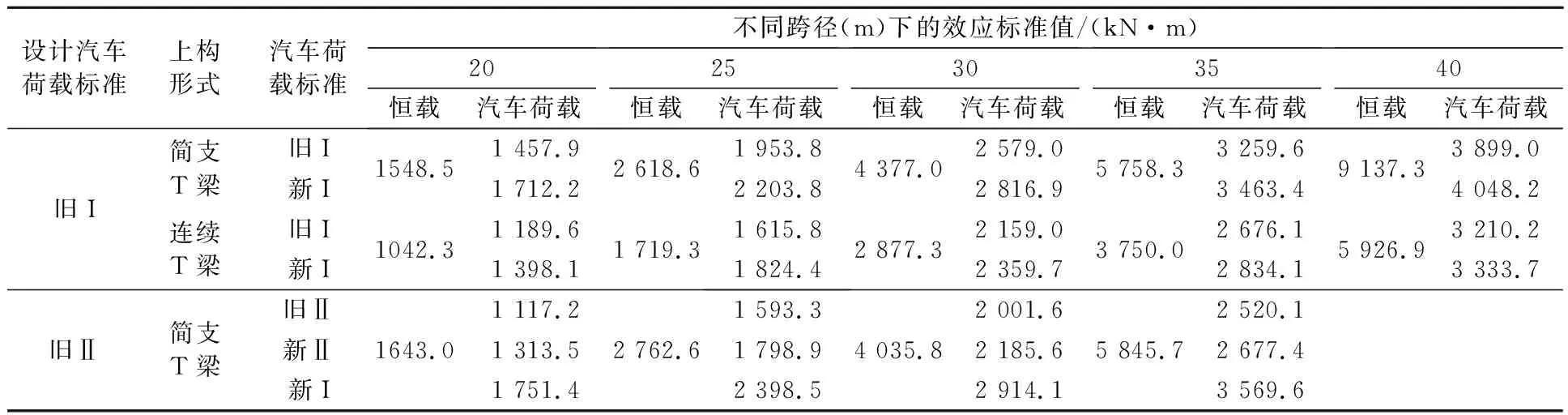
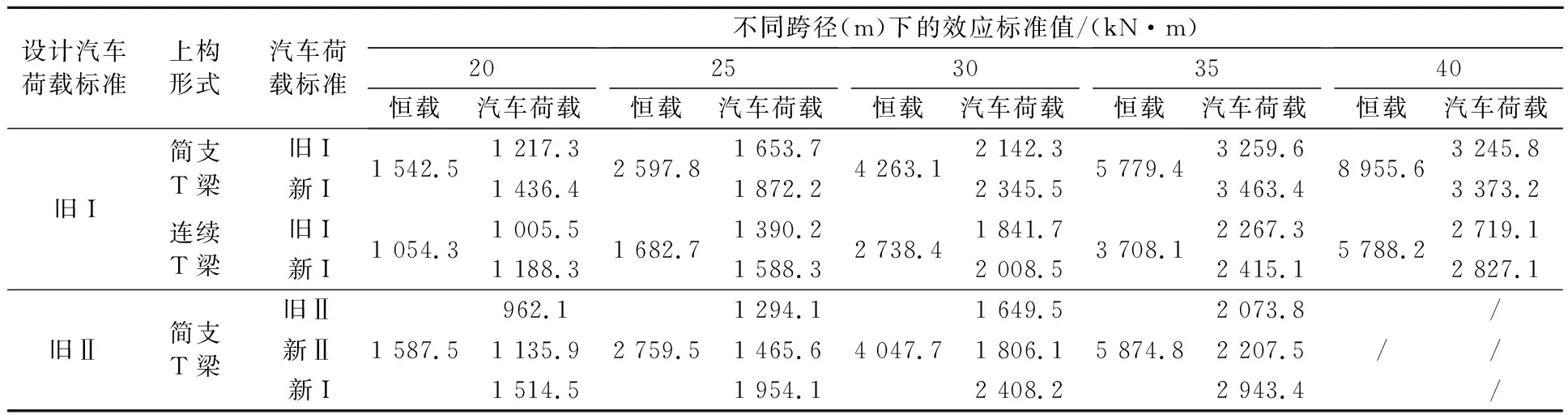
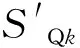
3.2 抗力富余需求系数计算

4 结 论
