国产原子钟的噪声及守时性能研究

宋会杰,董绍武,2,王翔，王燕平,张继海,屈俐俐，赵书红,张首刚,2

(1.中国科学院 国家授时中心，西安 710600；2.中国科学院大学 天文与空间科学学院，北京 100049)

0 引言

原子钟的噪声及守时性能分析是守时工作中非常重要的一项研究工作。原子钟噪声是影响时间稳定性的重要因素，分析原子钟的噪声特性，研究降低原子钟噪声的算法可以提升守时性能[1-4]。守时性能主要表现为产生标准时间的准确性、稳定性和实时性。利用原子钟的比对测量数据分析原子钟的性能，研究守时算法提升标准时间长期性能[5-9]。当前国内外研究人员对守时算法的研究不断取得新的进展，比如2014年后，国际权度局(BIPM)对原子钟进行二次模型预报并根据可预测性方法取权，提升了标准时间的整体性能[10-11]。目前我国采用的守时算法也是基于可预测性方法取权。但是上述研究和算法都是基于国外原子钟，比如美国的铯原子钟、氢原子钟和俄罗斯的氢原子钟等，由于国产原子钟的工作原理、材料、制造工艺与国外原子钟不同，导致噪声特性存在一定差异，因此研究国产钟的守时性能，提出符合国产钟特性的守时算法，解决我国标准时间自主产生和时间基准保持的核心技术是当前面临的迫切问题。文中基于小波分解研究了国产原子钟不同尺度下的噪声情况，并与国外原子钟进行了比较，计算出不同尺度下的噪声强度。通过经典加权算法与Kalman滤波算法分别计算基于国产钟的时间尺度，并比较了时间尺度的准确度、稳定度和实时性，整体上分析了基于国产钟的守时性能。

1 国产原子钟的噪声分析

小波变换作为一种时频局部化方法，其窗口是可变的，即在低频部分具有较低的时间分辨率和较高的频率分辨率，具有对信号的自适应性。应用于国产原子钟的测量数据，分析不同尺度的噪声强度。

1.1 小波变换的原理

(1)

‖Ψjk(t)‖=‖Ψ(t)‖j,k∈Z，

(2)

通过对国产钟测量数据进行离散小波变换，可以对数据进行时频分析，即测量数据在某一时间上，对应某一尺度a0的成分。相应的离散小波变换可表示为

(3)

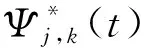
对于离散小波变换，一个3尺度的分解如图1所示。从图1可以看出小波变换分离信号的不同成分，其中不同尺度的低频系数表示去噪后的数据，不同尺度的高频系数表示噪声，对应国产原子钟不同频率段的噪声。

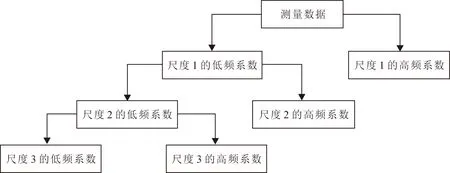
图1 3尺度分解的组织形式

1.2 基于小波变换的国产钟噪声分析

基于小波变换理论对国产钟的测量数据进行噪声分析，并与国外原子钟的测量噪声进行比较。国产原子钟编号选为Cs2025、Cs3050和Cs3059，国外原子钟编号选为Cs3089。测量数据时间为2020年8月至2021年6月，测量参考为UTC(NTSC)。利用db5小波对国产钟测量数据进行6尺度分解，得到不同尺度的原子钟噪声，其结果如图2，图3，图4和图5所示。为了清晰，图中只表示了3尺度分解。通过小波多尺度分解得出不同尺度噪声的标准差，其结果如表1和表2所示。结合图与表可以看出尺度越低，噪声越小，随着尺度的增大，噪声变大。小波分解中尺度越小，对应的频率越高，尺度越大，对应的频率越低。随着频率的降低，噪声变大，说明国产钟在低频段噪声明显，低频段的噪声对国产钟性能的影响起主要作用。守时算法需重点考虑降低国产钟低频噪声的影响。比较国产钟Cs2025，Cs3050和Cs3059不同尺度的噪声大小，在尺度1至尺度3，Cs2025和Cs3050的噪声明显低于Cs3059的噪声，说明国产钟Cs3059的高频噪声相对偏大。分析尺度4至6，Cs2025的噪声明显高于Cs3050和Cs3059，说明国产钟Cs2025的低频噪声相对偏大。3台原子钟，Cs3050的低频噪声与高频噪声都相对偏小，表示Cs3050的长期稳定度和短期稳定度最高。通过上述分析，得出不同原子钟的噪声情况不同，部分国产钟低频噪声相对偏大，部分国产钟高频噪声相对偏大。守时过程中，根据国产原子钟不同尺度的噪声情况进行加权处理，能够同时降低不同尺度噪声的影响，提升守时的整体性能。

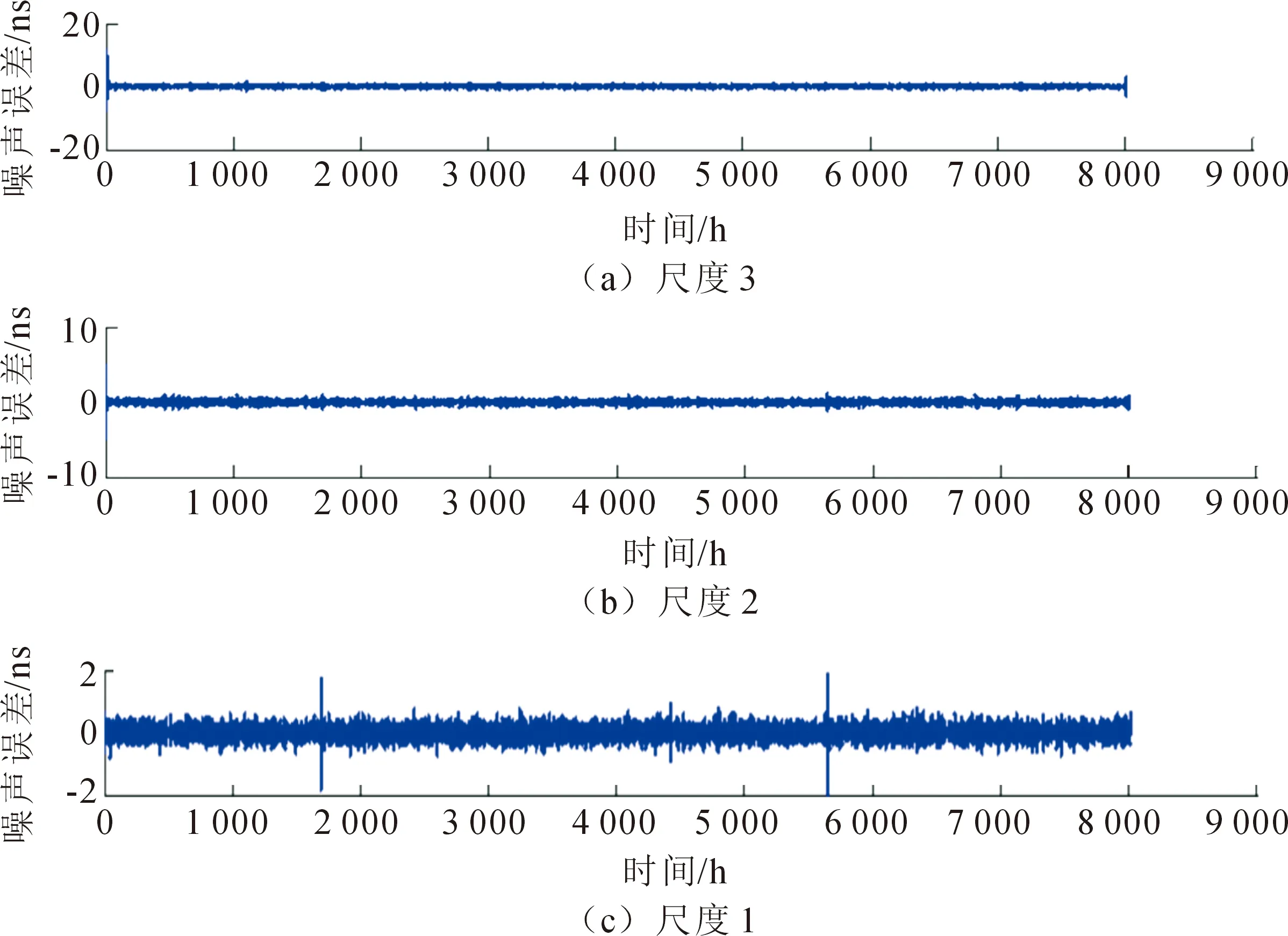
图2 Cs2025不同尺度的噪声

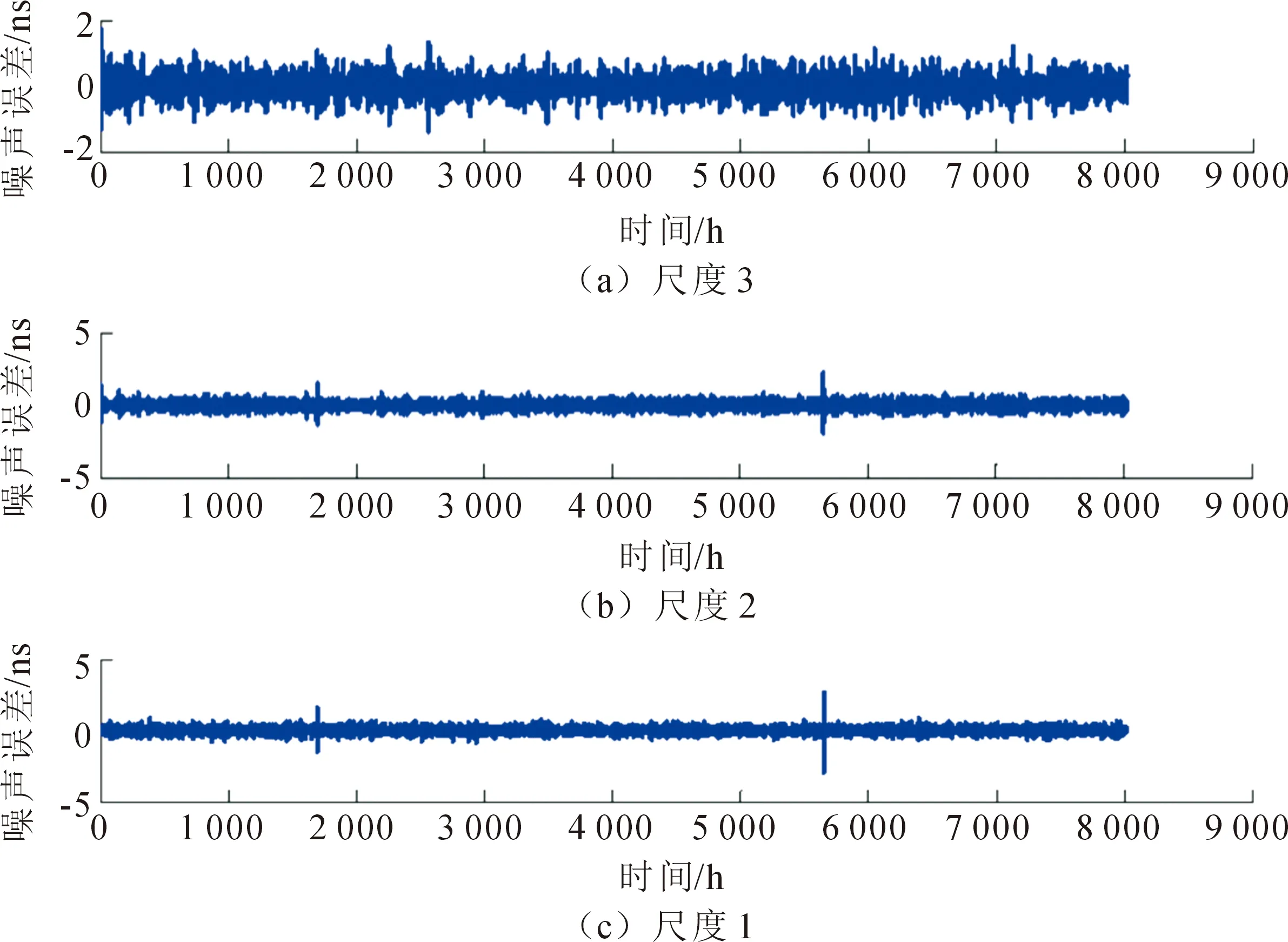
图3 Cs3050不同尺度的噪声

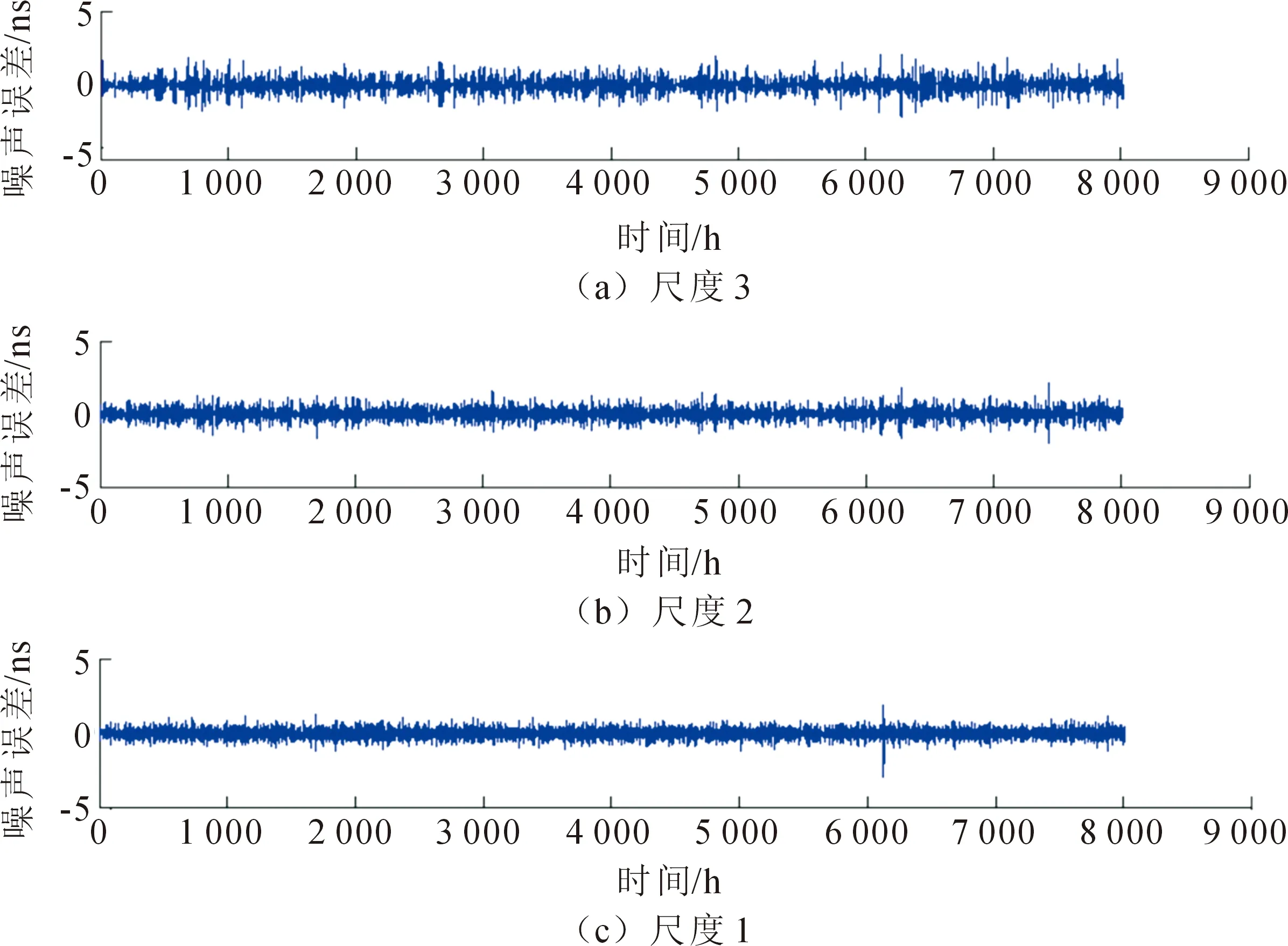
图4 Cs3059不同尺度的噪声

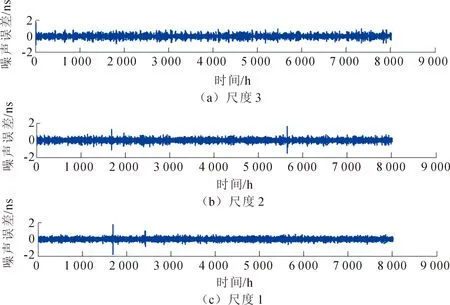
图5 Cs3089不同尺度的噪声

表1 原子钟尺度(1～3)的噪声标准差 单位：ns

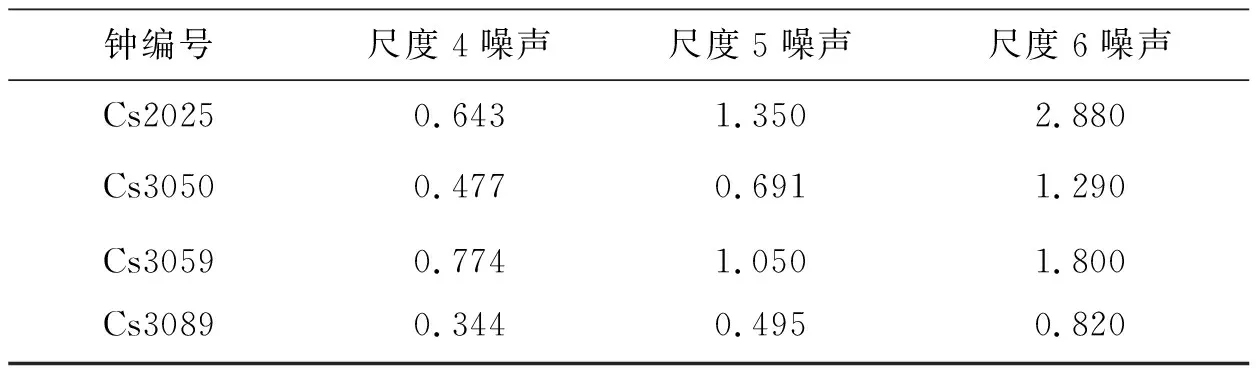
表2 原子钟尺度(4～6)的噪声标准差 单位：ns

2 国产原子钟的守时性能研究

守时性能通常表现为多台原子钟产生时间尺度的准确性、稳定性和实时性。在时间保持工作中，时间尺度相当于一台虚拟原子钟，这台虚拟原子钟是通过测量钟差实现的物理钟的加权平均。虚拟钟通过与某一台钟的偏差来表示。一般认为虚拟钟的性能优于单台原子钟的性能[5]。下面主要通过时间尺度算法研究国产原子钟的守时性能，重点研究一种Kalman滤波时间尺度算法用于国产钟的守时性能，并与一种经典的加权平均算法的守时性能进行比较。

2.1 钟的模型

Kalman滤波时间尺度算法是一种实时的原子钟状态估计方法，估计参考钟和理想钟之间的差，并将此值作为修正量，计算时间尺度。算法原理如下,原子钟的状态方程可表示为：

(4)

y(tk+1)=y(tk)+δω(tk)+η(tk),

(5)

ω(tk+1)=ω(tk)+α(tk),

(6)

式(4)至(6)中,x(tk)，y(tk)和ω(tk)分别表示钟在tk时刻的相位偏差，频率偏差和频率漂移偏差。tk和tk+1是相邻取样时间，具有如下关系，tk+1=tk+δ。ε(tk)，η(tk)和α(tk)分别表示tk时刻原子钟的调频白噪声，调频随机游走噪声和频漂随机游走噪声。原子在tk时刻的测量模型表示为

zij(tk)=xi(tk)-xj(tk)+v(tk),

(7)

式(7)中，zij表示第ith台钟和第jth台钟之间的相位差测量，v表示测量噪声。

Kalman滤波时间尺度问题是估计每台原子钟的状态，但是实际测量数据是钟差数据，因此建立钟差的状态方程估计原子钟的状态。通过方程(4)，(5)和(6)对钟i和钟j做差的钟差方程表示为：

(8)

yij(tk+1)=yij(tk)+δωij(tk)+ηij(tk),

(9)

ωij(tk+1)=ωij(tk)+αij(tk)。

(10)

根据N-1个钟差测量估计N台钟的状态，这种情况的解是不稳定的。根据中心极限定理，当原子钟数量很多时，噪声的加权和为0。即有下列辅助方程：

(11)

(12)

(13)

式(11)至(13)中,ai(tk)，bi(tk)和ci(tk)分别表示tk时刻钟i噪声的权重。根据钟差方程和辅助方程估计单台原子钟的状态。

2.2 Kalman滤波时间尺度算法原理

首先定义tk钟差状态变量和噪声向量为：

(14)

钟差方程的向量形式表示为

(15)

(16)

式(16)中，H表示测量矩阵，R是测量标准偏差。Kalman滤波的递推方程表示为：

(17)

(18)

(19)

(20)

Kij表示Kalman增益，表示为一个3-元素列向量：

(21)

式(20)结合式(14)的估计噪声向量为

(22)

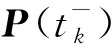
2.3 国产原子钟的守时性能研究

研究国产原子钟的守时性能，基于不同时间尺度算法分析国产原子钟的准确性、稳定性和实时性。选取国产原子钟，编号为Cs3050，Cs2025和Cs3059计算时间尺度，计算数据时间段为：2020年8月至2021年6月，数据采样周期为1 h，国产钟参考UTC(NTSC)的相对频率偏差数据如图6所示，为了表示清楚，Cs3059的相对频率偏差都减去1×10-12。从图6可以看出Cs2025的相对频率偏差相比Cs3050与Cs3059明显偏大，Cs3050与Cs3059的相对频率偏差相当。文中采用上述给出的Kalman滤波算法和经典加权平均(类ALGOS)算法计算国产原子钟的时间尺度，并分析时间尺度的准确度、稳定度和实时性。基于两种算法计算的时间尺度如图7所示，得出本文采用的类ALGOS算法计算的时间尺度长期波动较大，基于上述Kalman滤波算法的时间尺度长期波动相比本文采用的类ALGOS算法明显减小。分析原因，本文采用的类ALGOS算法采用前一个月的速率作为本月的预报值，如果本月速率相比前一个月的速率有一个较大的变化，会引起时间尺度较大的波动。Kalman滤波算法是一种实时算法，给定初始状态下根据测量钟差数据实时修正原子钟的状态估计，提高了时间尺度估计的准确性。表3给出了基于两种算法的时间尺度准确度指标，本文采用的类ALGOS算法的时间尺度与参考UTC(NTSC)的最大偏差为216.42 ns,明显大于基于Kalman算法的最大偏差128.42 ns；另外，类ALGOS算法的时间尺度与参考UTC(NTSC)偏差的平均值为33.19 ns，基于Kalman算法的时间尺度与参考UTC(NTSC)偏差的平均值为39.40 ns，两者相差不大；最后，基于本文类ALGOS算法的时间尺度的RMS为89.17 ns，明显大于基于Kalman滤波算法的RMS值52.63 ns，说明基于本文的类ALGOS算法的时间尺度长期波动大。基于以上分析，本文采用的Kalman滤波算法优于类ALGOS算法计算的时间尺度性能。

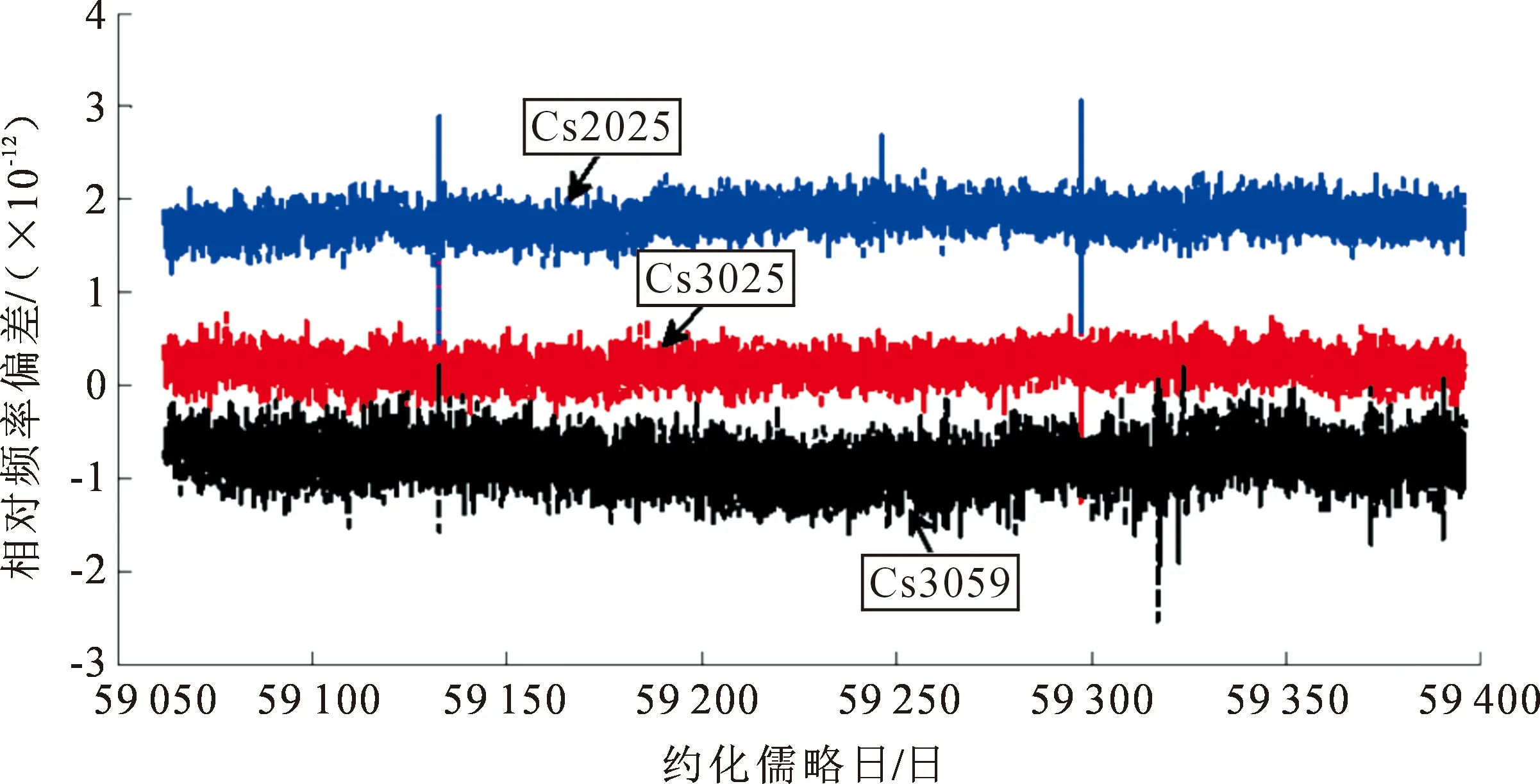
图6 国产原子钟的相对频率偏差数据

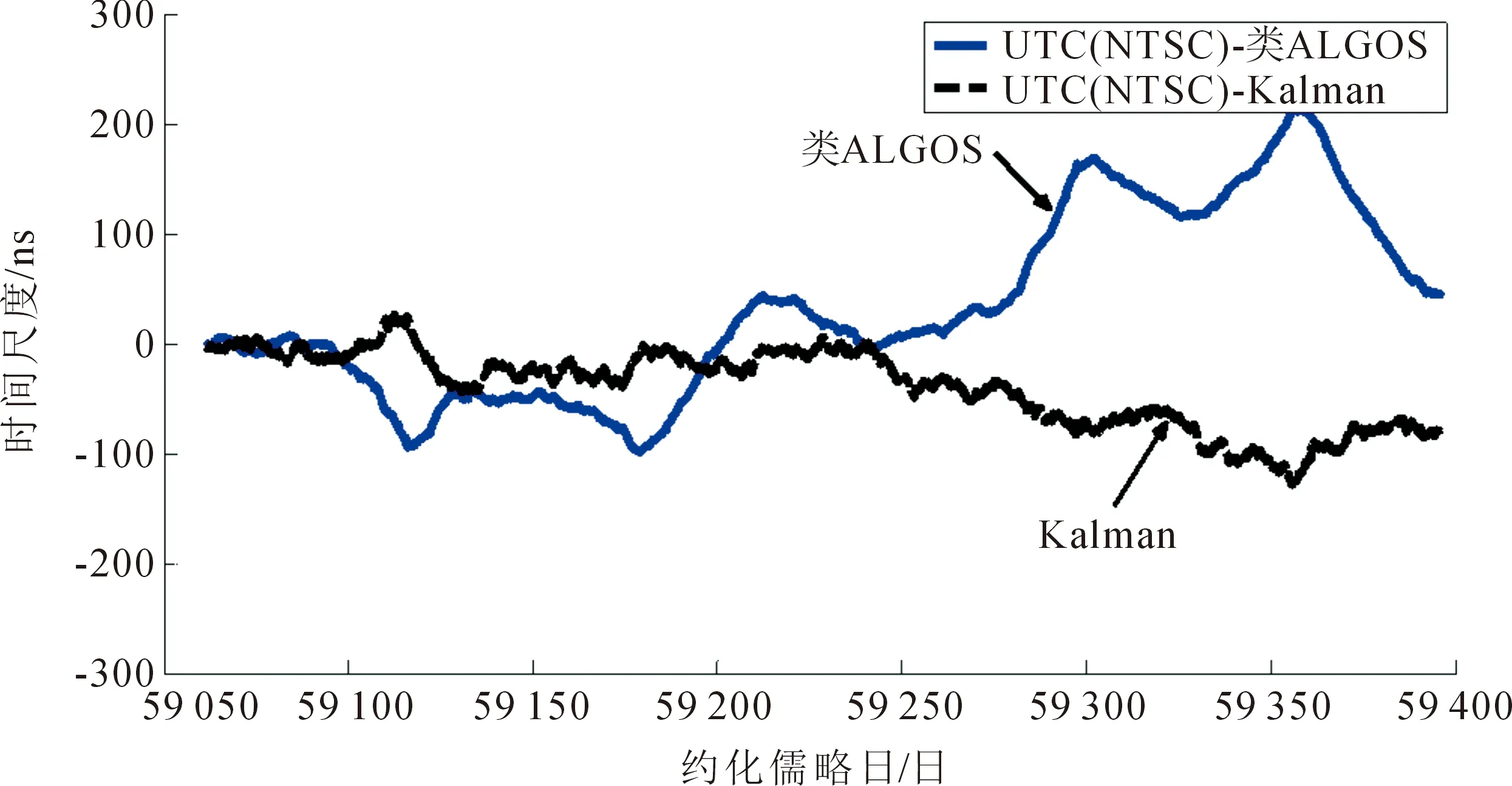
图7 基于两种算法的国产钟时间尺度

表3 基于两种算法的时间尺度的准确度 单位：ns

分析基于两种算法的时间尺度的稳定度，稳定度通过重叠Allan偏差表示，重叠Allan偏差越小稳定度越高,其结果如图8所示。从图8可以得出，不同国产原子钟稳定度差别明显，Cs2025和Cs3050稳定度性能10天内相差不大。10～83 d天内，Cs3050的稳定度明显优于Cs2025,Cs3059稳定度在相应取样时间差于Cs2025和Cs3050。说明相比较于Cs3050，国产钟Cs2025具有较差的长期稳定度，Cs3059短期稳定度和长期稳定度都明显低于其余两台国产原子钟。基于文中Kalman滤波算法计算国产钟的时间尺度，算法建立了钟差的相位偏差，频率偏差和频率漂移偏差的状态方程，并且状态方程中包括钟差的调频白噪声，调频随机游走噪声和频漂随机游走噪声。Kalman滤波算法通过使线性方差取极小值，同时降低了钟差状态方程中的多种噪声，提升了时间尺度的稳定度。图8给出了本文采用的类ALGOS算法计算的时间尺度的重叠Allan偏差和文中Kalman滤波算法计算的时间尺度的重叠Allan偏差。本文采用的类ALGOS算法计算时间尺度的重叠Allan偏差在相应取样时间均小于单台原子钟的重叠Allan偏差，30 d的重叠Allan偏差为2.9×10-14，83 d的重叠Allan偏差为1.1×10-14。基于Kalman滤波算法计算时间尺度在取样时间超过5 d后，重叠Allan偏差明显减小，稳定度显著提高，30 d的重叠Allan偏差为1.0×10-14，83 d的重叠Allan偏差为5.5×10-15。对于取样时间小于5 d，基于Kalman滤波算法计算时间尺度的重叠Allan偏差高于类ALGOS算法计算的重叠Allan偏差，甚至高于单台原子钟的重叠Allan偏差。分析原因，采用文中Kalman滤波时间尺度算法，首先需要给定钟差数据的初始状态，基于Kalman滤波算法估计预测状态，根据量测数据实时修正预测状态，给出钟差的估计，这是一个递推的过程。当原子钟可预测性变差时，Kalman滤波中量测数据不断的修正预测值，用于提高估计的准确性，这样就降低了时间尺度的短期稳定度。本文采用的类ALGOS算法计算时间尺度，根据前一个月的速率作为当前月的速率预报值，速率是恒定的，然后根据月速率的变化计算权重，这样降低了对时间尺度短期稳定度的影响。

图8 国产原子钟与时间尺度的重叠Allan偏差

对于实时性方面，本文采用的类ALGOS算法需要利用前一个月的速率作为当月速率的预报值，是一种滞后的时间尺度算法。Kalman滤波算法根据预测方程和量测方程递推的估计原子钟的状态，是一种实时的时间尺度算法。

3 结语

本文基于小波分解得到国产原子钟和国外原子钟的相应分解尺度的噪声，比较不同分解尺度的噪声大小，分析国产钟的性能。守时过程中，通过对多台国产钟在不同分解尺度加权处理，能够降低不同分解尺度的噪声，提升守时的性能。时间尺度的准确度、稳定度和实时性是守时性能的一个重要表现，时间尺度是由多台原子钟通过算法产生的一个纸面时间，国产钟守时的性能与时间尺度的性能有直接的关系。本文研究了基于国产钟的Kalman滤波时间尺度算法和本文采用的类ALGOS时间尺度算法，通过分析得出，Kalman滤波算法计算得到的时间尺度的准确度优于类ALGOS算法的准确度。5 d内，类ALGOS算法计算的时间尺度的稳定度优于文中Kalman滤波算法计算的稳定度；5～80 d，Kalman滤波算法计算的时间尺度的稳定度优于类ALGOS算法计算的稳定度。在具体实施方面，Kalman滤波算法具有较强的实时性。