LUT数字预失真在宽带GNSS信号的应用

王萌,卢晓春,饶永南

(1.中国科学院 国家授时中心，西安 710600；2.中国科学院大学 电子电气与通信工程学院，北京 101047)

0 引言

导航信号是联结卫星、地面运控以及用户的唯一纽带，其性能优劣将直接影响导航系统服务性能[1-3]。全球导航卫星系统(Global Navigation Satellite System，GNSS)通常采用恒包络复用(constant-envelope multiplexing，CEM)技术处理星上高功率放大器(high-power amplifier，HPA)引入的非线性问题[4-9]。然而，CEM信号通常假设滤波器无限带宽，受制于导航信号载荷限制，HPA前置限带滤波不可避免的破坏CEM信号的恒包络属性，经HPA放大后出现功率谱带外再生，相关曲线非对称跟踪锁相环抖动和载波跟踪误差等[10-14]。上述不利因素会干扰邻道业务，降低测距性能，对宽带调制信号的影响更为明显。例如，BDS-3系统 B2频点ACE-BOC调制信号等。此外，HPA引入的误差属于系统级误差，卫星间不尽相同，因此对HPA进行线性化处理可从系统层面保障信号质量。数字预失真(digital pre-distortion，DPD)是目前最具有潜力的HPA线性化技术，主要包括基于查找表(look-up table，LUT)和基于非线性模型两大方向[4,6]。国防科技大学李彩华[4]采用基于信号幅度与HPA联合概率的LUT DPD方案，讨论了索引函数对预失真性能的影响。郭宁雁[8]采用Hammerstein 预失真器，消除宽带ACE-BOC信号受HPA非线性影响，但前置限带滤波器效应考虑不足。中国空间技术研究院刘晗[9]采用星载数字滤波器分段的DPD，该方法有效的提升了主瓣带宽信号质量。上述方法中LUT DPD结构简单，可实现性强，规避了非线性模型求逆复杂的缺点，在通信卫星以及导航卫星HPA线性化领域引起了广泛关注。然而，该技术存在预失真精度与LUT插值基点数量相互制约的弊端，星上导航载荷有限的资源条件会影响LUT预失真效果[4,15-16]。针对该问题，本文基于LUT数字预失真，采用一种改进型非等距插值基点划分法来进行查找表分配。最后采用信号功率谱、相关函数、S曲线过零点偏差(S curve bias，SCB)来评估预失真前后信号质量的改善情况，详细内容见下文。

1 HPA非线性效应

在时钟监控单元驱动下(频综)，如图1所示，导航载荷发射链路主要由基带信号生成、抗混叠滤波、正交中频调制、D/A转换、上变频、前置限带输入滤波、功率放大、输出滤波及多工器合成，最后经天线发出[5-7,12]。

图1 导航载荷发射链路

导航载荷发射链路中，抗混叠滤波以及正交中频调制认为仅引入轻微的线性失真，D/A转换引起的Sinc衰落可采用数理手段补偿[7]。同时，忽略频综同源条件下基带信号生成和上变频单元引入的误差。输入滤波器是引起HPA非线性的重要原因，需要着重考虑。经过HPA后，信号输出滤波、多工器合成以及天线输出。此外，根据奈奎斯特采样定律，射频信号采样会造成巨大的计算量，本文将射频信号等效为基带信号来仿真分析。综上，如图2所示，导航载荷发射链路简化为理想基带信号生成，输入滤波器， HPA放大，输出滤波器，天线发射[5-7,12]。

图2 导航载荷发射链路简化模型

ACE-BOC调制信号主瓣带宽超过50 MHz[17]，采取该信号来仿真HPA非线性对宽带信号的影响，其中输入输出滤波器建模为理想低通滤波器。HPA采用Saleh模型，该模型采用幅度-幅度(AM-AM)以及幅度-相位(AM-PM)分别来表征HPA幅度和相位放大增益[18]，如图3所示，HPA在高幅值(功率)输入时呈现出明显的非线性特性。

图3 Saleh模型

如图4所示，输入滤波器无限带宽下，ACE-BOC信号星座点均匀分布在单位圆上，表明HPA对所有信号的放大增益是一致的。与之相反，图5中限带滤波(50 MHz)后HPA导致星座点呈现旋转以及发散现象。

图4 无限带宽滤波及HPA后星座图

图5 限带滤波及HPA 后星座图

图6合成功率谱残差中可看到限带滤波经HPA后输出信号出现带外再生谱，带内交调。以上均不利于GNSS信号质量，最终会带来测距误差。因此必须采取相应的技术手段减轻限带滤波以及HPA非线性对信号质量的影响。

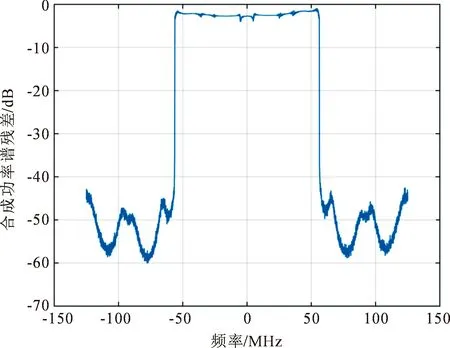
图6 经HPA 后合成功率谱残差

2 查找表数字预失真

2.1 极坐标查找表数字预失真

LUT DPD是将HPA逆特性(即预失真参数)以查找表的形式存储，在预失真时直接从表中调取参数的方案[4,15-16]。如图7所示，以输入信号x(t)幅值A(t)为自变量，根据索引函数F(A(t))寻找对应的插值基点D(i)提取参数A′(t)与θ′(t)，对输入信号与所提参数进行计算处理获取DPD的输出z(t)，因 DPD与HPA特性相反近似抵消，因而最终输出信号y(t)满足线性化需求。本文采用的Saleh非线性模型将信号幅度与相位分别讨论，故采用极坐标LUT方案。该方案将信号从直角坐标转换成极坐标模式，利用两个一维查找表分别存储幅度和相位预失真参数。

图7 极坐标查表预失真结构

基于极坐标查找表数字预失真算法流程如图8所示。

图8 预失真算法流程图

① 首先初始化查找表，幅度表A′(t)置1，相位表置0。根据索引函数进行地址索引，提取AM与PM参数A′(t)与θ′(t)，本文采取的索引方式为：min(abs(A(t)-D))，其中A(t)为输入信号幅值，D=[D(1),D(2),…,D(N)]代表插值基点，即选取距输入幅值最近的插值区间进行插值。

② 对提取参数进行运算处理z(t)=x(t)A′(t)exp(θ′(t))。其中A′(t)与θ′(t)分别为查找表存储的预失真器参数，x(t)为输入信号，z(t)为预失真器输出。(注：首次迭代时查找表为初始状态，所以z(t)=x(t))。

④ 重复②～③直至e(t)稳定收敛，完成预失真。

2.2 查找表插值基点划分

由2.1节可知，查找表对HPA逆特性的准确表征是预失真精度的关键，通常采用线性插值来提升LUT精度。如图9所示，将归一化输入信号幅值等间隔划分成N区间，间隔δ=1/N(图中N=10)。当幅值C落在A，B基点之间时，联立A，B可线性内插出C点参数。易知基点数量越多线性内插越精准，预失真效果愈佳。然而，导航载荷的限制导致预失真精度与插值基点数量相互制约的弊端。

图9 线性内插示意图

为了解决上述问题，基于“非线性区间多插值基点，线性区间少插值基点”理念，非等距离插值基点划分被引入。传统方法根据每一区间信号幅值占比来分配插值基点，在信号幅值分布均匀时具有一定优势，如图10所示，宽带GNSS信号滤波后会产生多幅度分布，且高幅值占比远低于低幅值分量，而该部分往往呈现强非线性，需要更多的插值基点来逼近HPA特性。本文采用一种仅依赖待插值函数输入输出特征曲线和容忍误差范围，无需显性函数表达式的非等距离插值基点划分法，该方法插值误差在相邻基点间正负交替出现，一定程度上减缓了误差累积效应[19]。如图11所示，该非等距离线性插值法原理如下所述。

图10 限带滤波后幅值分布 图11 非等距离线性插值基点原理图

假设F(x)为待插值HPA增益函数曲线，Δ为容忍误差范围，F+(x)、F-(x)分别为上下限误差函数曲线F+(x)=F(x)+Δ，F-(x)=F(x)-Δ。以基点(xi,F+(xi))为起点，对下限误差F-(x)做切线，根据点斜式插值法则：

(1)

根据所求切点(xii,F-(xii))，延长交于上限误差曲线F+(x)，交基点xi+1：

(2)

联立F+(x)及F-(x)，则待求解基点xi+1，插值函数F(x)以及误差Δ之间的关系为：

F(xii)-F(xi)+2Δ=F′(xii)(xii-xi)，

(3)

F(xi+1)-F(xii)-2Δ=F′(xii)(xi+1-xii)，

(4)

公式(3)和(4)为插值基点划分基本函数，按照(3)～(4)依次求解，可得到一系列的插值基点坐标(x0,x1,x2,…，xN)。由于相邻的两个插值基点严格控制在Δ内，且Δ是正负交替出现的，从而保障了插值精度。若HPA非线性输入输出函数为凹函数，则仅需变换相应的计算符号即可。

3 仿真验证

本节对LUT的数字预失真方案改善效果进行仿真验证，仿真参数如下：输入信号采用BDS-3 B2频点 ACE-BOC调制信号，采样率设置为250 MHz，前置滤波器带宽55 MHz，HPA非线性模型采用Saleh模型，参数采用第1节设置，后置滤波器带宽设置为50 MHz。

3.1 插值基点划分法比较

在插值容忍误差为10-3时，本文方法仅需30个插值基点，统计两种方法下不同区间插值基点占比示于表1。

表1 不同区间插值基点分布统计 单位：%

图12至图15给出两种方法下AM-AM和AM-PM增益曲线(求逆后)插值基点分布以及插值误差图。结合表1、图3和图10可知，在线性幅值区间[0～0.7)时，两种方法插值基点均与Saleh模型增益曲线符合度较好。本文方法在该区间基点占比约23.32%，而传统方法为80.01%。在幅值区间为[0.7～0.9)时Saleh模型已呈现出弱非线性，两种方法基点占比相当分别为20%和16.66%，本文方法侧重将更多的基点分配在[0.8～0.9)内，而传统方法则是[0.7～0.8)，此时传统方法已出现轻微的不匹配现象，这也说明本文方法对增益函数的非线性更适应。参考图10，在幅值区间为[0.9～1.0)时，虽然信号分量占比较少，但该区间呈现强非线性对预失真的优劣起决定作用，传统方法在该区间基点占比仅为3.33%，相邻插值基点的连线明显与Saleh增益曲线不匹配，仅两基点处符合。与之相反，新方法占比达到56.68%，有效地保障了强非线性区间不存在空域的现象，确保该区域的预失真参数拟合精度。上述分析表明，本文方法资源分配更加合理，在线性区域分配较少的资源，在非线性较强的区域，分配较多的资源，这样和有效降低预失真中查找表的更新时间，提升预失真精度。

图12 AM-AM插值基点分布图

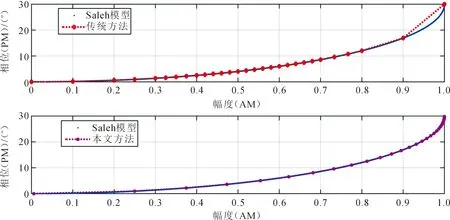
图13 AM-PM插值基点分布图

图14 AM-AM插值误差

图15 AM-PM插值误差

3.2 信号质量评估

信号功率谱反映了信号能量随频率的变化情况，可直接观察出信号功率谱有无明显的载波泄露，带外抑制情况[1-3]。导航信号失真可直接反映为相关函数异常，利用相关函数可评估导航信号相关功率损耗及测距性能的优劣[1-3]。归一化相关函数定义为

(5)

式(5)中，sRec(t)为载波剥离后接收信号，sRef(t)为本地参考信号；积分时间TP为主码周期。S曲线反映了不同相关器间隔下的测距性能，理想的S曲线过零点应位于码跟踪误差为零处，由于卫星载荷、空间信号传输通道和地面接收通中滤波器带限、多径等影响会引起码环锁定存在偏差[1,3，13]。以非相干超前减滞后鉴相器为例，设其相关器间隔为δ，则S曲线的表达式为

(6)

锁定点偏差εbias(δ)满足：

Scurve(εbias(δ),δ)=0。

(7)

S曲线过零点偏差(S curve bias,SCB)为锁定点偏差最大最小差值：

Scb=max(εbias(δ))-min(εbias(δ))。

(8)

图16和图17给出了预失真前后以及不同插值方法下的信号功率谱对比图，信号未进行预失真时，信号功率谱出现明显的带外再生，带内与理想信号轻微不符合。而预失真后带外功率谱出现了明显的抑制，带内与理想信号符合度较好，且新方法下，带外再生频谱相较于传统方法下降约10～15 dB。

图16 功率谱对比图 图17 合成功率谱残差对比图

图18给出了预失真前后相关函数曲线对比图，未预失真时相关函数对称轴偏移0处，相关峰峰值出现明显的下降造成功率损失，图19显示预失真后，两种方法相关峰峰值相当，新方法峰值略大于传统方法，对称效果更优。

图18 预失真前后相关函数对比图 图19 不同划分法相关函数对比图

图20给出了预失真前后，S曲线锁定点偏差对比图，由图可知，由HPA引入的S曲线锁定点偏差在相关器间隔0.35码片处高达0.18 m，而预失真后，不同相关器间隔下锁定点偏差均小于0.01 m，测距性能有了明显提升。图21给出了相关器间隔0～1码片内两种方法下SCB和插值基点的对应关系图，由图可知，本文方法比传统方法率先达到稳态，整体性能优于传统方法。当插值基点为较小时(<50)，或较大时(>1 000)两种方法趋于稳定，两种方法效果相当,相差约0.01 ns；当插值基点为90时，本文方法SCB性能优于传统方法0.033 ns；而当SCB为0.002 ns时，传统方法需要800多个基点，而本文方法仅需90个基点，大幅度节省了硬件资源。

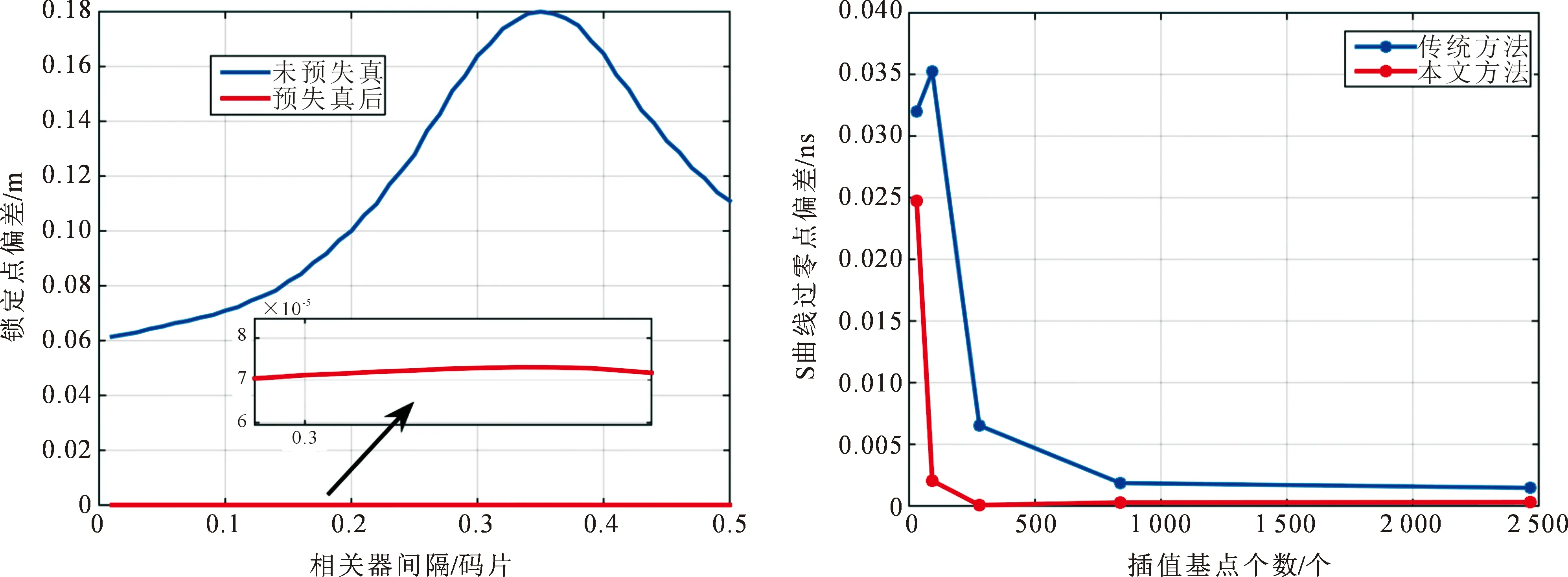
图20 预失真前后锁定点偏差对比图 图21 S曲线过零点偏差与插值基点对应关系

综上，在插值基点固定时，本文方法测距性能更优；在测距性能一定时，本文方法所需插值基点更少，能根据HPA特性曲线进行灵活合理的插值基点划分。

4 结语

围绕着导航载荷发射链路高功率放大器对宽带导航信号的影响，本文采用基于极坐标LUT算法对星上HPA进行了预失真研究，该算法采用新型的LUT插值基点划分方法，可根据HPA特性合理有效地分配资源。以功率谱、相关函数及S曲线过零点偏差作为预失真前后信号评估准则。现得出结论如下：① 在查找表插值基点数量固定30时，该算法带外功率谱下降约10～15 dB，S曲线过零点偏差由0.12 m下降至0.01 m内，表明该算法能有效提升导航信号质量。② 在查找表插值基点固定时，本文方法测距性能更优；在测距性能一定时，本文方法所需插值基点大幅度下降，能在保障预失真精度的同时有效地节省硬件资源。