一种原子钟频率净化的环路最优带宽求解方法

鄢然，刘军良，郑晓龙，武建锋，胡永辉

(1.中国科学院 国家授时中心，西安 710600；2.中国科学院大学，北京 100190；3.火箭军工程大学，西安 710025)

0 引言

高质量的时频信号是导航定位、时频计量、航空航天等众多领域的基础条件，通过高精度锁相环技术实现原子钟频率净化，以获得高质量时频信号是工程实践中常采用的方法[1]。原子钟频率净化技术是通过一个高性能的锁相环，将原子钟频率优良的长期特性与高稳压控振荡器(voltage controlled oscillator，VCO)良好的短期特性结合起来，使得输出频率信号既能保持原子钟良好的长期稳定度，同时又获得较好的短期稳定度。图1为原子钟频率净化框图。同时国内外各大时频设备生产厂商的原子钟频率净化设备，例如中国天奥生产的XHTF3328A、美国Microsemi生产的4145C、俄罗斯VREMYA-CH生产的VCH-317、德国Timetech生产的Clean-up Oscillator等均基于这一思路构建各自的频率净化系统[2]。

图1 原子钟频率净化框图

为了获得最佳的净化效果，锁相环环路的工作带宽通常选取最优带宽。为了得到最优的环路带宽，文献[2-7]提及环路最优带宽的求解规则，即锁相环环路的最优带宽应该选取在参考相位噪声功率谱密度与VCO相位噪声功率谱密度交点的横坐标附近(本文称“相噪交点法”)，但该规则的成立近乎理想，且未曾考虑不同类型、不同阶数的锁相环对该规则的影响情况；文献[8-11]分析了锁相环的相位噪声为确定信号前提下的环路最优带宽表达式，而这样的表达式无法应用于原子钟频率净化，因为影响原子钟频率不稳定的噪声不仅仅是白噪声，往往还有有色噪声。文献[12-13]结合锁相环环路特性分析了锁相环中的相位噪声，并指出在环路带宽内，输出信号相位噪声可以约等于参考源相位噪声；在环路带宽外，输出信号相位噪声约等于VCO相位噪声。过往学者关于锁相环最优带宽的研究表明，准确地选取锁相环环路带宽对原子钟频率净化的效果有着至关重要的影响。本文将从影响环路带宽选取的相位噪声入手，针对几种不同类型不同阶数的锁相环环路特性，结合相噪交点法，利用开环增益穿越频率点与相位噪声相交频率点的偏离程度，对最优带宽进行求解并评估。

1 基本理论

1.1 锁相环环路带宽

锁相环环路带宽的选取对原子钟频率净化的效果有着重要的影响。以一个基本结构的锁相环为例，如图2所示。定义其开环传递函数G(s)、闭环传递函数H(s)如下：

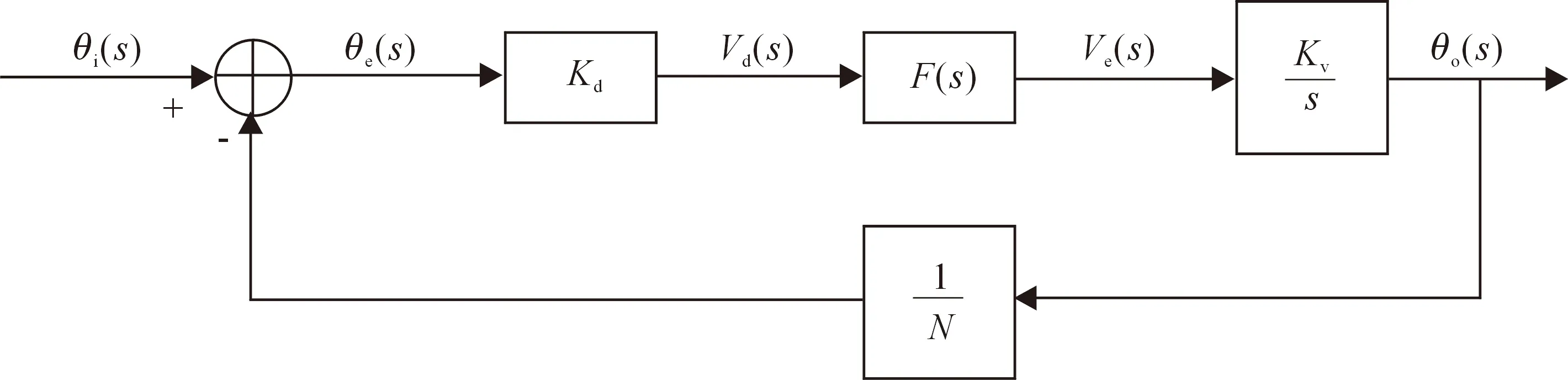
图2 锁相环S域信号传递关系

(1)

(2)

式(1)和(2)中:θi(s)、θo(s)、θe(s)分别表示输入、输出、相差信号相位的拉普拉斯变换；s是拉普拉斯变换域中的复频率；Kd为鉴相器系数，单位为V/rad；Kv为VCO系数，单位为rad/(V·s)；F(s)是环路滤波器的传递函数；N为分频器的系数。

对于锁相环环路带宽有很多种定义，固有频率ωn、噪声带宽BL、环路增益K，其中文献[14]中对环路带宽定义如式(3)，单位为Hz，适用于任何类型的锁相环，故本文所提及的环路带宽即

K=KdKvK1Fhf(0)，

(3)

式(3)中，K1是环路滤波器的无量纲比例系数，Fhf(0)是滤波器“高”频部分的极值。

1.2 幂律谱噪声模型

对于原子钟频率净化系统而言，频率源是锁相环的基本单元，一个设计良好的净化系统，相位噪声应该主要来自频率源[14]。幂律谱噪声模型是使用最广泛的频率源噪声模型，它的有效性已经被许多实验结果所证实，并为国际学术界所普遍接受[15]。在原子钟频率净化系统中，其参考源相位噪声与VCO相位噪声均可用幂律谱噪声模型来表征。其噪声钟差的功率密度谱函数用5种相互独立的随机噪声来描述振荡器的频率波动过程，表达式为

(4)

式(4)中，hα为常数，α=-2,-1,0,1,2分别对应着频率随机游走噪声、频率闪烁噪声、频率白噪声、相位闪烁噪声、相位白噪声5种不同的噪声类型。fh为频率测量过程中低通滤波器的截止频率。

本文采用了文献[15]提及的原子钟钟差产生方法，产生了不同参考源(MHM2010氢原子钟、HP5071A铯原子钟、PRS10铷原子钟)与OCXO 8607高稳晶振的噪声钟差序列，并绘制了不同参考源与高稳晶振VCO的相位噪声谱密度如图3所示。

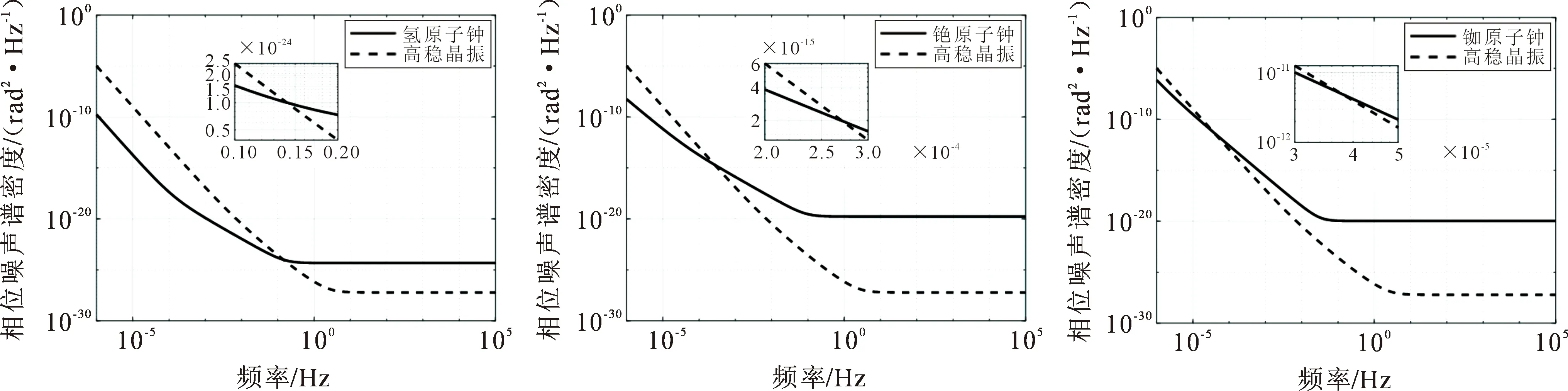
图3 不同类型原子钟与VCO相位噪声功率谱密度

从图3可以看出，根据相噪交点法，不同类型的原子钟与VCO的相位噪声功率谱密度确有一交点，且对于MHM2010氢原子钟、HP5071A铯原子钟、PRS10铷原子钟的频率净化的环路最优带宽分别在K1=0.14 Hz,K2=2.7×10-4Hz,K3=3.8×10-5Hz附近。

在仅考虑参考源和VCO相位噪声的锁相环系统中，根据环路传输模型，输出信号相位的通式为

(5)

式(5)中，φref(s)，φvco(s)为参考源、VCO的相位噪声；H(s)，E(s)为环路闭环传递函数和误差传递函数。

因此，输出信号相位噪声功率谱密度为

Sθo(f)=|H(f)|2Sφref(f)+|E(f)|2Sφvco(f)。

(6)

式(6)中，Sφref(f)和Sφvco(f)分别表示参考源和VCO的功率谱密度函数。从式(6)可得知，环路的闭环传输函数、误差函数和参考源相位噪声、VCO相位噪声均对系统输出信号的相位噪声有着重要的影响。

2 最优环路带宽求解方法

锁相环环路的最优带宽被定义为使得输出信号相位抖动最小的频率点[16]。相位抖动的计算是对输出信号的相位噪声功率密度谱进行积分，可以理解为相位噪声功率密度谱与坐标轴所围成的面积。单一使用“相噪交点法”没有考虑锁相环的闭环传输函数、误差函数对输出信号的相位噪声的影响，这样的使用规则近乎理想化，可以表达为下式：

(7)

从式(7)可知，“相噪交点法”是在式(6)的基础上衍生而来，其忽略了环路传输函数与误差函数的交点是否与参考源、VCO相位噪声功率谱密度交点重合的问题，而这一点忽略极有可能导致输出信号Allan偏差在交点附近恶化，出现“鼓包”现象。

基于以上对环路输出信号相位噪声和单一使用“相噪交点法”弊端的分析，本文提出了结合闭环传递函数与误差传递函数幅频特性曲线的交点ωc与环路带宽K的偏离程度来求解并评估环路最优带宽。

环路闭环传递函数与误差传递函数幅频响应曲线相交的频率点被定义为开环增益穿越频率ωc，并以Hz为单位。同时，ωc亦是使得|G(jωc)|=1的频率点。

图4绘制了一组MHM2010氢原子钟、高稳晶振的相位噪声谱密度与二阶二类锁相环环路函数幅频响应的特性曲线。

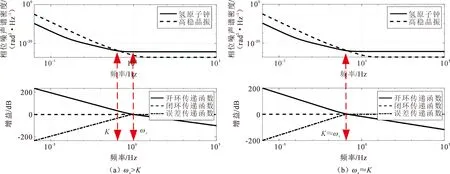
图4 “环路函数交点法”结合“相噪交点法”评估环路最优带宽

图4通过对比分析了同一组频率源相位噪声及VCO相位噪声在二阶二类锁相环ωc>K与ωc≈K的两种情况。结合式(6)，可以得到，若ωc>K，那么系统输出的相位噪声低通部分不再主要受参考相位噪声的影响，还将受VCO相位噪声的影响，其输出相位噪声为

Sφo(f)=|H(f)|2[Sφref(f)+Sφvco(f)]+|E(f)|2Sφvco(f)。

(8)

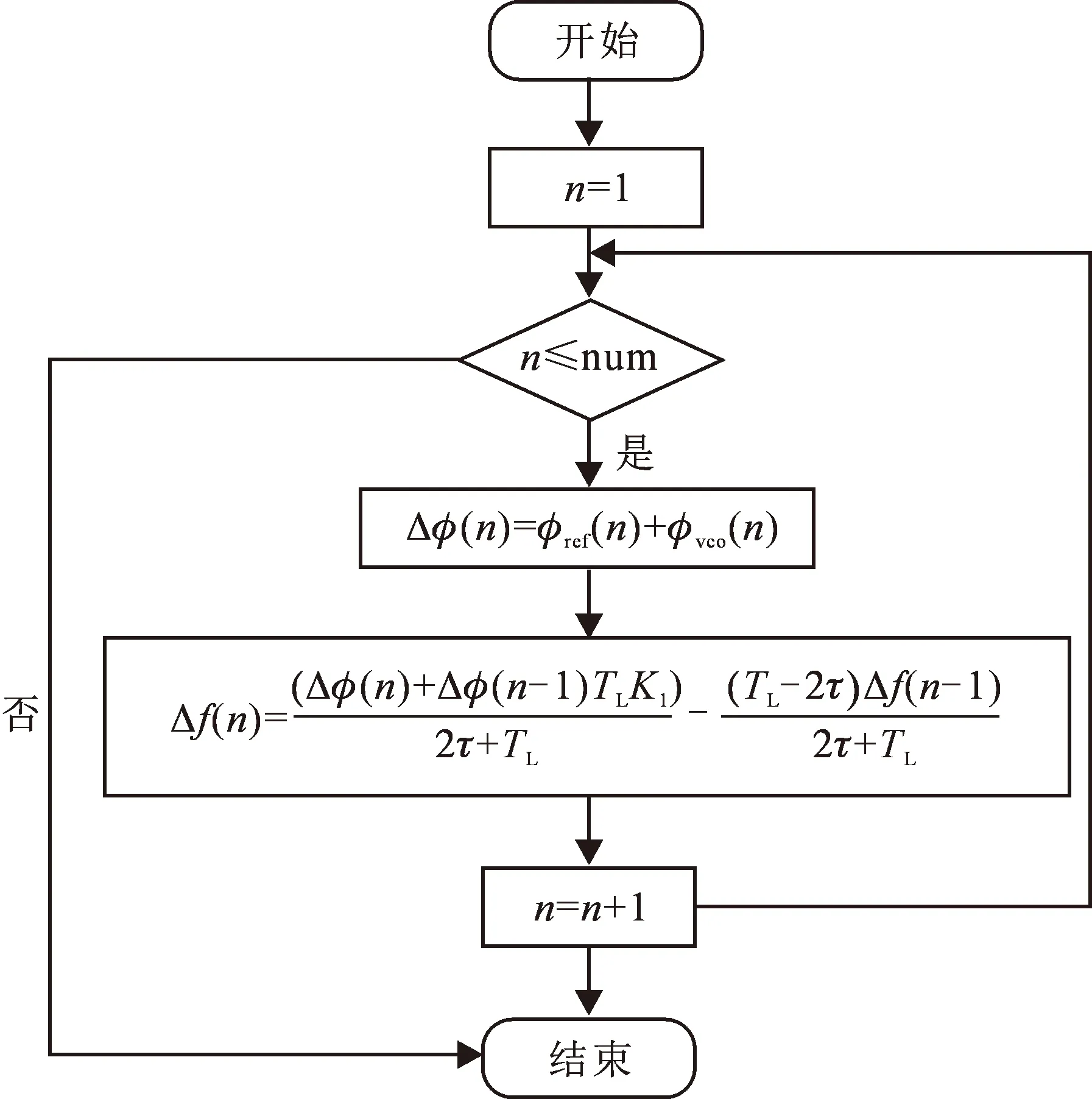
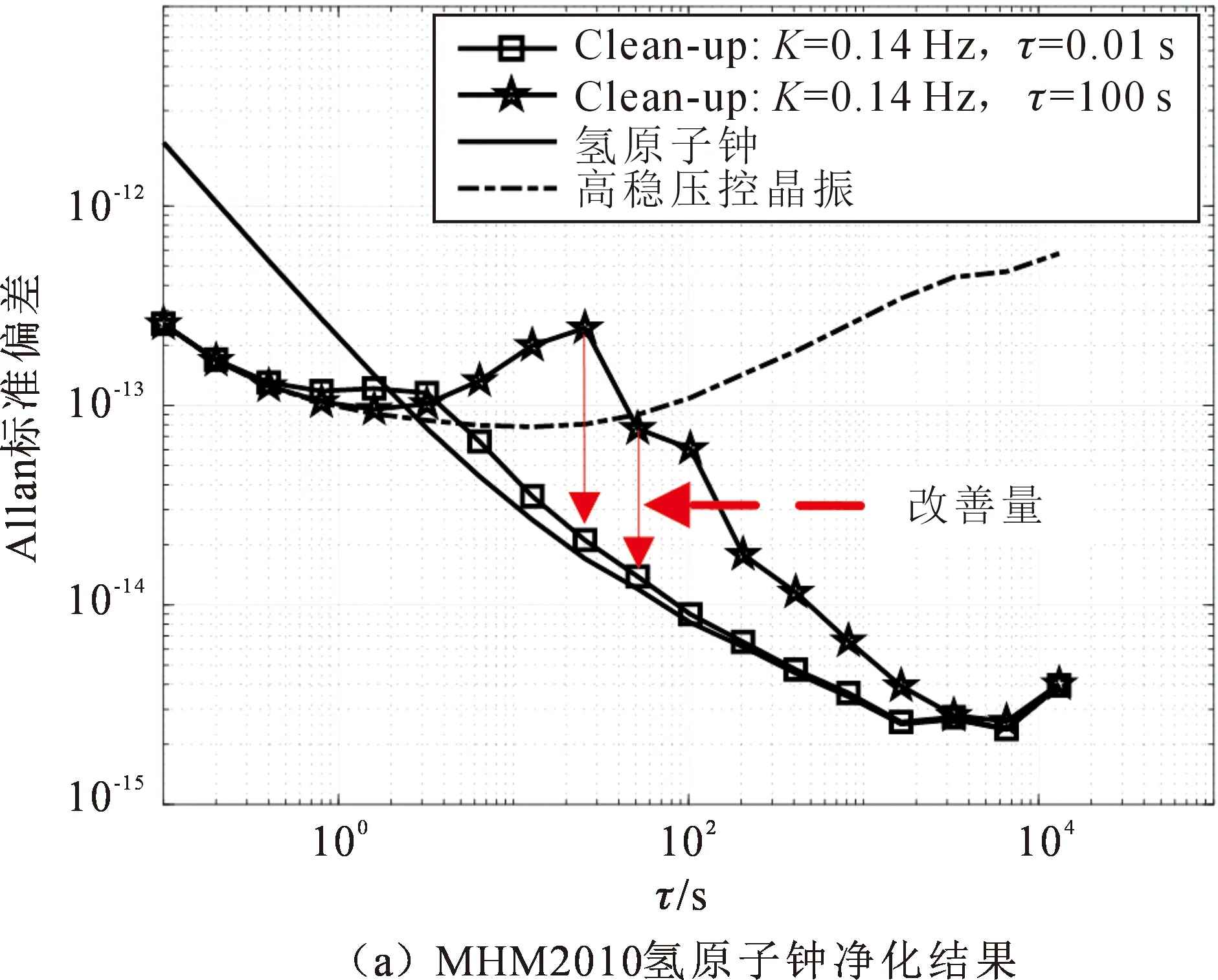
同理，若ωc

对于原子钟频率净化而言，一阶锁相环的研究看似意义不大，但是往往能从一阶锁相环环路行为近似推广到较为复杂、较难分析的其他阶数、其他类型锁相环。因此对于一阶锁相环有，F(s)=K1，Fhf(0)=1，它的开环增益穿越频率有：

(9)

ωc=K。

(10)

从式(10)可以得知，对于一阶锁相环而言，开环增益穿越频率ωc和环路带宽K相等。而对于其他几种类型、阶数的锁相环，开环增益穿越频率ωc与环路带宽K的关系均可由式(9)进行计算，具体结果如表1所示。

表1 几种不同类型不同阶数锁相环增益穿越频率与环路带宽关系

从表1可以得知，单一使用“相噪交点法”存在一个默认ωc≈K的前提条件，而通过上述的论证可以看出，只有一阶锁相环才满足该条件，而其他类型、其他阶数的锁相环需在一定限制条件下才满足ωc≈K。

根据以上的分析可以得知，仅仅根据“相噪交点法”来确定环路最优带宽是一种不严谨的方法，通过结合本文提出的“环路函数交点法”共同求解并评估环路最优带宽将更为准确、可靠。

3 仿真验证

为了验证单一使用“相噪交点法”的局限性，及本文提出的“环路函数交点法”结合“相噪交点法”求解环路最优带宽的正确性，以带滞后滤波器二阶锁相环为例，仿真对比分析了在满足ωc≈K及ωc≪K两种条件下，不同类型原子钟的频率净化效果。

3.1 原子钟频率净化算法实现

文献[17]指出，在使用双线性变换法的二阶环路设计中，归一化噪声带宽小于0.1时，数字锁相环系统可以使用模拟锁相环的方法进行分析。因此，参考原子钟及高稳晶振VCO输出信号相位可分别表示为：

φref(n)=2πf0t(n)+2πf0xref(n)，

(11)

和

φvco(n)=Δφ(n-1)+2πf0t(n)+2πf0xvco(n)。

(12)

式(11)和(12)中：f0为标称频率；t(n)为仿真时间；xref(n)，xvco(n)分别代表了参考源和VCO的相位噪声钟差；Δφ(n-1)表示在n-1时刻VCO输出信号与参考源信号相位偏差量。两信号在通过鉴相器之后的信号相位差可表示为

Δφ(n)=φref(n)-φvco(n)。

(13)

环路滤波器表达式为

(14)

通过双线性变换可以得到其在离散域的表达式为

(15)

式(15)中，Y代表了环路滤波器的输出，X代表了环路滤波器的输入。利用Z的逆变换可得

(2τ+TL)y(n)=(x(n)+x(n-1))TLK1-(TL-2τ)y(n-1)。

(16)

在本文中，y(n)代表了环路滤波器在n时刻输出的频偏Δf(n)，x(n)代表了环路滤波器在n时刻的输入即鉴相器的输出Δφ(n)。在得到了n时刻VCO输出信号相对于参考源信号的相对频偏后，则有

Δφ(n)=Δφ(n-1)+2πf0(t(n-1)-t(n))。

(17)

本文的算法实现如下所述：

①利用式(11)和(12)分别产生标称频率f0=10 MHz，时间间隔为1 s，数据长度为1×106的参考原子钟和VCO信号相位数据；

②设置环路参数，例如Kd=1(V/rad)，Kv=1(rad/(V·s))，因此环路带宽为K=K1，环路更新时间TL=1 s，因此环路的更新次数num为106次。

③循环求得两信号之间的相位差Δφ(n)，并通过环路滤波器得到相对频率偏差Δf(n)，用于对VCO进行频率调整，如图5所示。

图5 原子钟频率净化算法流程图

④通过锁相环的作用，VCO输出信号相位最终与参考源信号相位同步，实现频率净化。

3.2 原子钟频率净化结果

由图3可知，参考原子钟(MHM2010氢原子钟、HP5071A铯原子钟、PRS10铷原子钟)相位噪声功率密度谱与VCO相位噪声功率密度谱交点的横坐标分别在K1=0.14 Hz，K2=2.7×10-4Hz，K3=3.8×10-5Hz附近。在仿真试验中，根据“相噪交点法”的原则，这3个频率点将作为环路的最优带宽带入不同类型锁相环进行原子钟频率净化仿真。图6(a)，(b)，(c)分别为MHM2010氢原子钟、HP5071A铯原子钟、PRS10铷原子钟频率净化仿真试验结果，其中通过设置环路带宽K及环路滤波器时间常数τ，使得其均满足Kτ≈0，从而满足ωc≈K，输出信号Allan标准偏差以方框线型表示；为了形成对比，唯一改变环路滤波器时间常数τ，使ωc≪K，输出信号Allan标准偏差以五角星线型表示。

图6 不同类型原子钟的净化结果

图6对比分析了不同类型原子钟在带滞后滤波器二阶环路下的频率净化仿真结果。其中实线线型代表着参考源相位噪声的Allan标准偏差，虚线线型代表着VCO相位噪声的Allan标准偏差，方框标记的线型代表着输出信号在满足ωc≈K条件下的Allan标准偏差，五角星标记的线型代表着输出信号在ωc≪K条件下的Allan标准偏差。从图中可以看出，在满足ωc≈K条件下(方框线型)，不同类型的原子钟的频率净化效果最佳，输出信号同时具备优秀的长、短期稳定度；而在ωc≪K时(五角星线型)，净化效果不佳，且集中表现为在交点附近出现“鼓包”。而这样一种现象，也正是因为其ωc≫K或ωc≪K，导致输出信号在通过环路时，低通部分不再主要受参考相位噪声的影响，还受VCO相位噪声的影响或高通部分不再主要受VCO相位噪声的影响，还将受参考相位噪声的影响。

图6证实了本文提出的“环路函数交点法”结合“相噪交点法”求解的环路最优带宽均使得不同类型原子钟频率净化取得了良好的净化效果。在带滞后滤波器的二阶锁相环下，氢原子钟频率净化效果改善明显，净化后的输出信号Allan标准偏差由2.44×10-13@ 26 s提高至1.77×10-14@ 26 s，最佳改善略大于1个量级；铯原子钟频率净化效果较明显，由8.17×10-13@ 4 096 s提高至1.76×10-13@ 4 096 s，最佳改善大于0.5个量级；铷原子钟频率净化后的信号Allan标准偏差由7.87×10-13@ 16 384 s提高至4.14×10-13@ 16 384 s，改善小于0.5个量级。

4 结论

本文针对几种不同类型不同阶数的锁相环，在“相噪交点法”的基础上，根据开环增益穿越频率与环路带宽的偏离程度，提出了一种原子钟频率净化的锁相环环路最优带宽的求解方法。通过仿真验证了该方法，验证结果表明在锁相环开环增益穿越频率约等于环路带宽时，求取的最优带宽在不同类型原子钟频率净化中均能得到良好的净化效果，输出信号Allan标准偏差均有不同程度的改善，最大改善量可略大于1个量级；反之，均有不同程度的劣化，集中表现为交点附近的“鼓包”现象。本文提出的“环路函数交点法”结合“相噪交点法”可更为快速、简便、直观地评估环路的最优带宽。