鸭舵式迫击炮弹气动特性研究

张嘉易王晓赫郝永平赵洪力薛 超

(1.沈阳理工大学 机械工程学院，沈阳 110159；2.辽宁省先进制造技术装备重点实验室，沈阳 110159；3.辽沈工业集团有限公司，沈阳 110045)

传统弹丸空气动力分析通常采用试验测量与理论分析两种方法。试验测量法主要以风洞试验作为基本手段，可得到较为真实可信的结果，但由于成本高、周期长等原因，难以实现对每种设计方案均进行试验；理论分析法可以得到普遍性结果，但需要抽象、简化研究对象，且在非线性条件下难以得到精确解。计算流体动力学(Computational Fluid Dynamics，CFD)方法综合了上述两种方法的优点，其以流动基本方程为基础，通过离散化方法获得复杂问题的数值解。

近年来，国内外学者基于CFD方法对弹丸气动特性进行了大量的研究工作[1]。De Spirito等[2]对某旋转火箭弹在马赫数为0.4~4.5时进行了气动计算，得到了阻力、法向力、俯仰力矩等气动参数，结果表明CFD计算可以得到可靠的气动参数值，计算值与试验值相差均在允许范围内。郝永平等[3]运用滑移网格技术对两对固定翼二维修正弹进行气动特性研究，结果表明随着马赫数的增加，控制力矩、减旋力矩及阻力均增加。刘琦等[4]研究了舵偏角对火箭弹气动特性的影响，结果表明，弹丸舵偏角越大，其升力系数越大。张嘉易等[5]分析了不同形状、不同面积鸭舵的各项气动参数，结果表明大展弦比舵翼可以获得较大升力和偏航力。

目前，对于固定鸭舵修正弹气动特性分析较为成熟，而对仅有一对鸭舵修正弹气动特性的研究则较少。一般情况下，固定鸭舵式修正弹采用两对固定翼舵头，通过同向舵与差动舵相互配合进行弹道修正，而一对鸭舵修正弹利用舵翼适时偏转以获取修正力；两者修正方式和舵翼数量均有所不同，从而对弹体的气动特性产生不同的影响，进而影响弹丸飞行稳定性。因此，对于一对鸭舵式修正弹进行相关的气动研究十分必要。

本文以某新型迫弹为研究对象，采用Fluent软件对其进行气动仿真，获得其外部绕流流场，分析迫弹在不同马赫数与攻角条件下的空气动力系数及空气动力矩系数的变化情况，以及舵偏角对舵翼受力的影响，通过比较双翼型和四翼型鸭舵的仿真结果，得到双翼型鸭舵修正弹的气动特点。在进行新型弹加工试验前进行大量的气动仿真计算分析，对新型弹的研究具有很好的借鉴与指导意义。

1 数值模拟方法

本文研究对象为某新型迫弹，修正舵翼呈“一”字形排列，其模型如图1所示。

图1 某新型迫弹模型

1.1 控制方程

采用雷诺平均三维可压缩N-S方程作为弹丸外部流体流动的基本控制方程[6]，忽略热源与体积力，其形式为

式中:t为时间；xi为坐标变量；Q为流动守恒变量；Fi为无黏通量；Fvi为有黏通量。各项具体表达式为

式中:ρ为流体密度；ui、uj、uk均为速度分量；E为单位质量总能；p为压强；H为单位质量总焓；τij、τki为黏性应力；qi为热流量；δij为Kronecker符号，i＝j时其值为1，i≠j时其值为0。

1.2 湍流模型

Fluent软件内置湍流模型多样化，涉及航天、化工等多个工程领域。本文采用Spalart-Allmaras(S-A)湍流模型，该模型可较好地模拟弹体外部绕流流场，同时也为解决控制方程不封闭问题，对雷诺应力项应用Boussinesq假设附加一个运动涡(湍流)黏度输运方程。相比其他湍流模型，S-A模型为单方程模型，求解计算量较小、鲁棒性好，同时不必计算剪切层厚度值，较为适合研究空气流动问题。S-A模型引入变量~v是Boussinesq假设应用于单方程模型中的体现，~v表示近壁区(主要受到黏性影响的区域)以外的湍流运动黏性系数，其方程为[7]

式中:Gv是湍流黏性产生项；Yv是由于壁面阻挡与黏性阻尼引起的湍流黏性减少项；σ~v和Cb2为常数；μ为动力黏性系数；xj为坐标变量。

1.3 网格划分及无关性验证

整体网格主要采用非结构化网格划分技术。非结构网格的尺寸容易控制、划分速度快，与复杂曲面贴合性较好，可有效减少划分网格时间、提高弹体数值模拟整体效率。将划分的网格模型导入Fluent软件，在控制台输入网格重新排序命令，将排序后的网格转化成多面体形式网格。多面体网格划分优势明显，在同等精度要求下，多面体网格划分需要的网格量、占用内存及计算机求解时间均明显少于四面体网格，其求解过程收敛性能更佳，基本不用调整求解器参数[8]。弹体和外流域网格划分结果如图2和图3所示。

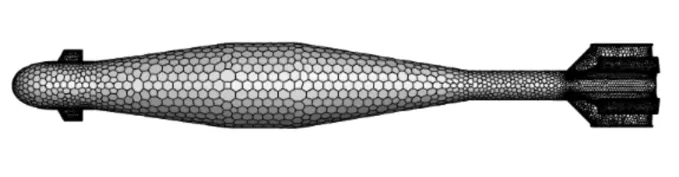
图2 弹体网格

图3 外流域网格

网格数量对仿真计算结果影响较大，因此通过对比4种不同数量网格的计算结果，进行网格无关性验证分析[9]。选取来流条件:马赫数为0.8，攻角为4°，舵偏角为0°。选择网格数量N分别为100万、300万、500万和700万，分别对弹体外部流场进行数值模拟，得到弹丸阻力系数，以不同网格数量下的阻力系数进行网格无关性验证，计算结果如表1所示。

表1 网格无关性验证计算结果

由表1可见，与网格数量为700万时的阻力系数相比，网格数量为100万、300万和500万时阻力系数的相对差值分别为3.54%、1.79%和0.323%。考虑计算时间和计算结果，后续计算网格数量设置为500万。

2 仿真结果分析

2.1 弹体气动特性分析

本文研究的迫弹属于尾翼稳定弹，弹丸转速设为5 r/s，弹体低速旋转主要目的是消除不对称因素影响、减少射弹散布。弹丸速度一般在跨音速区，将来流速度区间设为马赫数0.8~1.2，攻角设为0°、2°、4°、6°、8°，舵偏角保持0°不变。

在舵偏角为0°、来流马赫数为1.2、攻角为0°时仿真计算得到弹体压力云图，如图4所示。

图4 弹体压力云图

由图4可以看出，在弹头、鸭舵、变截面弹体、尾翼等处出现了压缩波与膨胀波。钝体弹头处形成脱体激波，气流受阻被压缩，产生高压区，压力增大，速度减小；在变截面弹体处形成膨胀波，此时截面尺寸由大变小，气流流向发生改变，压力减小，速度增加；当空气流过鸭舵时，气流外折，速度增加，压力减小；气流到达尾翼时，流动受阻，速度减小，压力增加。本文得到的压力云图与文献[10]中弹体超音速飞行时的特点一致。

保持舵偏角为0°不变，在不同来流马赫数下计算得到阻力系数随攻角变化曲线，如图5所示。

图5 阻力系数随攻角变化曲线图

由图5可见，攻角不变时，随着马赫数增加，阻力系数增大；马赫数不变时，阻力系数随攻角增加而增大。弹丸亚音速飞行时阻力主要有摩擦阻力、压差阻力以及诱导阻力，超音速飞行时除了上述阻力外，还由于空气的压缩性而产生波阻，当马赫数增加时，波阻的影响效果更为显著，故阻力系数增大。攻角增大时，弹体壁面外的附面层与其发生分离，气流逐渐呈旋涡状流动，旋涡内部存在低压区，使得弹体前后形成较大的压差阻力，故阻力系数增大；随着攻角进一步增加，阻力系数成二次曲线型增长，这是因为攻角增大，诱导阻力迅速上升，而诱导阻力系数近似与攻角平方成正比[11]。

以马赫数为0.8时的弹丸为例，采用Matlab软件拟合阻力系数Cx与攻角α的关系曲线，得到拟合方程，并略去方程中一次项，整理如下。

亚音速飞行条件下，弹丸阻力系数与攻角关系呈现如式(7)所示的二次函数变化规律[11]。

式中:Cx0为零升阻力系数；K为攻角系数。

对比式(6)和式(7)可知，本文拟合方程与文献[11]给出的方程形式一致。

保持舵偏角为0°不变，在不同马赫数下计算得到升力系数随攻角变化曲线，如图6所示。

图6 升力系数随攻角变化曲线图

由图6可见，相同马赫数下，升力系数随攻角的增加近似呈线性增长，且攻角较小时线性程度更好；攻角不变，升力系数随马赫数增加而增大。由于攻角增大，使得弹体升力方向分量增加，因而升力系数增大。该结果与文献[11]给出的尾翼弹升力系数变化规律一致，即马赫数不变、小攻角条件下，升力系数-攻角变化曲线近似为直线，且保证正攻角产生正向升力。在跨音速区，空气可压缩性影响更加明显，随着空气速度增加，其可压缩性使得弹体上表面压力降低更多，从而升力增加，升力系数增大。

保持舵偏角为0°不变，在不同马赫数下计算得到俯仰力矩系数随攻角变化曲线，如图7所示。

图7 俯仰力矩系数随攻角变化曲线图

由图7可见，马赫数不变时，俯仰力矩系数随攻角增大呈曲线上升；攻角一定时，马赫数增加，俯仰力矩系数增大，但增加趋势逐渐减缓。当马赫数、攻角增大时，压心位置后移，质心与压心距离变大，使得俯仰力矩系数变大。由于弹体坐标系z轴正向对应于Fluent坐标系z轴负向，故图7中俯仰力矩均为正值。由文献[12]可知，俯仰力矩系数与弹体静稳定性密切相关，当其为负值时，表示此时弹体静稳定。故本文模拟的弹体处于静稳定状态。

2.2 舵翼气动特性分析

上述分析均在舵偏角不变的前提下进行，由数值模拟结果可以得到不同攻角及马赫数下弹丸所受空气动力及动力矩的一般规律。现分析不同马赫数下舵偏角对舵翼受力的影响。将来流速度设置为马赫数0.8~1.2、攻角取值范围2~8°、舵偏角变化范围-8~+8°，舵翼横截面形状为对称双圆弧形，纵截面形状为直角梯形。

在舵偏角为8°、马赫数为1.2、攻角为8°时仿真计算得到舵翼横截面压力云图，如图8所示。

图8 舵翼横截面压力云图

由图8可以看出，舵翼前缘阻滞气体流动，气流在此积聚、速度减缓，形成高压区；舵翼下侧(迎风面)所受压力明显比上侧(背风面)所受压力更大，此时两侧形成压力差，此即鸭舵式迫弹修正力及修正力矩的来源。通过适时改变舵翼偏角，获得修正力(矩)的作用，以进一步实现对弹体纵横两个维度上的修正。

攻角为4°时，计算得到不同马赫数下弹体舵翼力随舵偏角的变化曲线，如图9所示。

图9 舵翼力随舵翼偏角变化曲线

由图9可见，舵翼力随舵偏角增加而增大，相同舵偏角下舵翼力大小基本相同；当舵偏角不变时，舵翼力随着马赫数的增加而增大，且超音速时舵翼力的增加幅度明显大于亚音速时的增加幅度。舵偏角为0°时，舵翼主要受空气黏性力影响；舵偏角不为0°时，舵翼除了受黏性力影响外，还会受到来流对舵翼的压力作用。故舵偏角为0°时，舵翼力最小。

为进行比较分析，在相同条件(马赫数为1.2，攻角为0°，舵偏角为8°)下，分别对双翼型和四翼型鸭舵进行仿真计算，得到压力云图和涡旋迹线图，如图10所示。

图10 两种舵翼对比图

由图10(a)和图10(b)可见，同向偏角双翼型迎风面压力大于背风面，截面压力云图呈对称形式，而四翼型压力云图由于存在反向偏角的差动舵，其截面云图并不对称。由图10(c)和图10(d)可见，与双翼型比较，四翼型舵翼产生的涡旋较多，并且涡旋轨迹线更加密集，随着其向后发展会对尾翼产生微小气动干扰。

3 结论

本文以鸭舵式修正迫弹为研究对象，通过数值模拟方法对弹体及舵翼进行相关的气动特性分析，得到如下结论。

(1)当舵偏角为0°时，弹丸的阻力系数、升力系数和俯仰力矩系数均随攻角和马赫数的增加而增大；在小攻角条件下，升力系数随攻角的变化具有较好的线性关系。

(2)舵偏角不为0°时，舵翼两侧的压力差产生弹体的修正力及修正力矩。当马赫数不变时，舵翼力随舵偏角的增大而增大；相同舵偏角条件下，马赫数越大，舵翼力越大。

(3)与四翼型比较，双翼型鸭舵的压力分布均匀对称，能够达到较为满意的修正效果；同时其产生涡旋更少，减小了对尾翼的气动干扰，能够保持整弹良好的气动特性。

本文结论可为后续迫弹的设计及研究提供一定的参考。