不锈钢打底TIG焊接电流拟合分析

2023-01-16杨婷婷武小娟

沈阳理工大学学报 2023年1期

杨婷婷，武小娟

(沈阳理工大学材料科学与工程学院，沈阳 110159)

不锈钢因其良好的耐腐蚀性、焊接性、低温塑韧性及良好的综合力学性能，在工业领域得到广泛应用[1]，其中焊接加工的不锈钢中厚板结构件主要用于工程机械、船舶桥梁等。对于质量要求较高的不锈钢焊接构件，在采用埋弧焊等焊接方法填充焊及盖面焊前，需要进行高质量的打底焊接[2]。打底焊道是保证焊接质量的关键，在焊接作业时打底焊道的存在保证焊件既能被焊透，又不至于被烧穿，能有效提高焊接质量。钨极惰性气体保护焊(TIG)作为一种焊接质量高、过程稳定的焊接方法，被广泛应用于打底焊接[2]。

在不锈钢打底TIG焊接过程中，焊接质量受焊接电流等参数的影响，在实际施焊过程中施工人员一般根据经验选择焊接参数，因此对施工人员的经验与技术水平要求较高。Matlab软件在数据处理和分析方面具有强大的功能，其自带的曲线拟合工具箱中包含曲线拟合函数及应用程序，能够对数据进行预处理和后处理[3]。对于不锈钢打底TIG焊，可采用Matlab对各参数之间的关系进行拟合，根据拟合方程简单快捷地确定焊接电流，以弥补打底焊接电流多依靠经验确定的不足。

本文通过查阅文献，收集不同板厚的实际焊接电流数据，利用Matlab软件提供的polyfit函数及Curve Fitting曲线拟合工具箱确定板厚与焊接电流的最佳曲线关系，为实际焊接生产中参数的选择提供依据。

1 数据的获取

为保证拟合结果的合理性，查阅文献得到两种不同来源的实际焊接电流数据，分别编号为来源1[4]和来源2[5]。不同板厚下不锈钢打底TIG焊实际焊接电流数据如表1和表2所示。

表1 不同板厚下的焊接电流(来源1)

表2 不同板厚下的焊接电流(来源2)

焊接条件及材料:钨极氩弧焊，接头形式为对接，平焊，单道焊，焊接电流极性为直流正接，母材为不锈钢，其他焊接工艺参数与焊接电流相匹配。

2 基于Matlab的焊接电流曲线拟合

2.1 曲线拟合原理

焊接生产过程中得到的焊接电流通常为离散数据，曲线拟合可根据离散数据生成平滑曲线，准确反映出离散数据间的关系[6]。

最小二乘法是解决曲线拟合问题最常用的方法，多用于科学研究和工程技术领域中处理数据并确定变量之间的关系[7]。其原理是，样本回归函数被解释变量的值与已知样本数据点值的总体误差最小，即在坐标图中解释变量值相同的情况下拟合函数上所有被解释变量点与已知样本数据点的垂直距离最小[8]，但不要求拟合曲线经过每个点。

基于最小二乘法，Matlab提供了多种曲线拟合方法，如利用函数进行曲线拟合，常用的拟合函数有polyfit函数和lsqcurvefit函数，以及利用Curve Fitting曲线拟合工具箱等[9]。本文采用polyfit函数及Curve Fitting工具箱相结合进行曲线拟合。

2.2 焊接电流曲线拟合

以来源1与来源2中给定的焊接电流为取值范围，应用Matlab进行曲线拟合时需要选定用来拟合的具体焊接电流数值。

由表1中数据可知，来源1中同一板厚下焊接电流最大值、最小值、平均值相差较小，且某些板厚下焊接电流为定值，因此拟合时对来源1数据选用焊接电流平均值。由表2中数据可知，来源2中同一板厚下焊接电流最大值、最小值、平均值相差较大，为保证拟合精度，对来源2中数据分别采用焊接电流最大值、最小值、平均值进行拟合，并通过与来源1中数据的拟合结果进行对比分析，确定适宜的焊接电流取值范围。

2.2.1 多项式拟合阶次的确定

根据对不同来源焊接电流变化趋势的分析，选择Matlab中的polyfit函数进行多项式曲线拟合，根据优化度分析结果确定合适的多项式次数。由于高阶多项式拟合会产生龙格现象，故多项式拟合的次数不宜过高[10]，本文分别采用一阶、二阶、三阶多项式对焊接电流数据进行拟合。

来源2的数据中焊接电流最大值与焊接电流平均值、最小值相差较大，但变化趋势几乎相同，故在确定拟合次数时，以焊接电流平均值为例确定最优的多项式拟合次数。

(1)来源1数据的初步拟合曲线及方程

对来源1数据分别进行一阶、二阶、三阶多项式曲线拟合，得到的拟合曲线如图1所示。

图1 来源1数据的多项式拟合

图1(a)中拟合得到的一阶曲线方程为

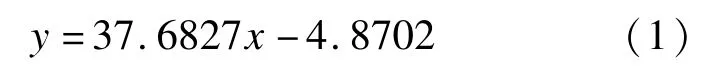
式中:y为拟合后的焊接电流；x为板厚。

图1(b)中拟合得到的二阶曲线方程为

图1(c)中拟合得到的三阶曲线方程为

(2)来源2数据的初步拟合曲线及方程

对来源2数据分别进行一阶、二阶、三阶多项式曲线拟合，得到的拟合曲线如图2所示。

图2 来源2数据的多项式拟合

图2(a)中拟合得到的一阶曲线方程为

图2(b)中拟合得到的二阶曲线方程为

图2(c)中拟合得到的三阶曲线方程为

(3)拟合曲线优化度分析

拟合曲线的优化度表示拟合的优劣程度，Matlab软件中Curve Fitting工具箱提供误差平方和(SSE)、决定系数(R-square)、校正决定系数(Adjusted R-square)及均方根误差(RMSE)等4个参数评价拟合效果。

对于拟合得到的不同阶次曲线，在样本数据相同的情况下，SSE与RMSE均反映拟合误差的大小，其值越接近于0，说明拟合结果越优[11]。Rsquare反映自变量对因变量的解释能力，其值越接近1，说明自变量对因变量的解释能力越强，拟合结果越优；Adjusted R-square考虑了曲线拟合的复杂程度，可对添加的非显著变量给出惩罚，其值越接近1，表示拟合曲线越合理。

使用Curve Fitting工具箱对拟合曲线处理后得到来源1和来源2数据的各阶拟合曲线评价结果，如表3和表4所示。

表3 各阶拟合曲线评价结果(来源1)

表4 各阶拟合曲线评价结果(来源2)

比较表3中的数据可以看出，对于来源1的数据，二阶拟合和三阶拟合曲线与原始数据的拟合度均较好，各项参数相差不大，均优于一阶拟合曲线。

比较表4中的数据可以看出，对于来源2的数据，三阶拟合曲线与原始数据的拟合度较好，优于一阶和二阶拟合曲线，一阶和二阶拟合曲线的各项参数相差不大。

综上分析，采用三阶多项式拟合的结果更优。

2.2.2 焊接电流取值范围的确定

前已拟合得到来源1和来源2数据中焊接电流平均值的三次拟合多项式，在此基础上，进一步对来源2数据中的焊接电流最大值和最小值进行三次多项式拟合，在Matlab脚本文件中编写程序并运行。为使拟合曲线趋势表达更为明显，在板厚x为0.8~4 mm的范围内等间隔地取12个数据点绘制拟合曲线，如图3所示。

图3 焊接电流的三阶拟合曲线

图3中对来源2数据中焊接电流最大值和最小值拟合得到的三阶曲线方程分别为

由图3可见，当板厚在0.8~4 mm时，各拟合曲线均表现出焊接电流随板厚增加而增大的趋势。当板厚介于0.8~2.5 mm之间时，焊接电流最大值位于式(7)表示的曲线上，焊接电流最小值位于式(3)表示的曲线上；当板厚为2.5 mm时，式(3)和式(8)表示的曲线相交；当板厚为2.5~4 mm时，焊接电流最大值位于式(7)表示的曲线上，最小值位于式(8)表示的曲线上；当板厚约为4 mm时，式(3)和式(7)表示的曲线相交。因此，不锈钢打底TIG焊接时，不同板厚下的焊接电流取值范围为:当板厚为0.8~2.5 mm时，由式(3)和式(7)分别计算焊接电流的最小值和最大值；当板厚为2.5~4 mm时，由式(8)和式(7)分别计算焊接电流的最小值和最大值。

根据拟合曲线分析结果，绘制板厚在0.8~4 mm范围内的焊接电流取值范围，如图4所示，两条曲线中间部分即为焊接电流取值范围。