内啮合强力珩齿工件齿面珩削纹理预测与控制方法研究

2023-01-16李振富田晓青费宁忠

中国机械工程 2023年1期

韩江李振富田晓青费宁忠夏链

1.合肥工业大学机械工程学院，合肥，230009 2.安徽省智能数控技术及装备工程实验室，合肥，230009 3.上海纳铁福传动系统有限公司，上海，201315

0 引言

随着新能源汽车的飞速发展，传统内燃机逐渐被电机取代，汽车传动装置的噪声开始受到重点关注，齿轮作为汽车变速箱的重要零部件，其加工精度和表面质量对变速箱噪声有重要影响。目前大多数齿轮在热处理后常采用磨齿和珩齿等精加工工艺来获得较高的加工精度和表面质量[1]。磨齿加工的精度一般可达5级，但齿面产生的平行纹理在高速齿轮副啮合过程中容易发生周期谐振，产生噪声；内啮合强力珩齿是目前工业中应用最多的珩齿工艺，由于其特殊的加工形式，具有较高的加工效率，同时形成特殊的弧线纹理能有效避免谐振问题、提高齿面的储油能力[2]，因此高性能变速器齿轮副常采用珩齿工艺或一磨一珩的工艺组合[3]。齿轮表面加工纹理对齿轮啮合噪声有重要影响，为降低变速器噪声，需对齿面纹理进行设计及优化。

在珩齿加工过程中，珩磨轮易发生磨损，使被珩工件的加工精度和表面质量下降[4]，严重时可导致工件不合格或珩磨轮报废，为保证加工过程的正常进行，需要定期对珩磨轮进行修整，利用金刚修整环和金刚修整轮将珩磨轮表面材料去除，使其露出新的磨粒，重新获得切削能力。但珩磨轮的修整会改变原始的加工条件，影响加工齿轮质量的一致性[4]，因此，研究不同的加工条件对珩齿齿面纹理的影响对齿轮加工具有重要意义。

SCHWEICKERT[5]对比了工件与珩磨轮间不同轴交角对珩削纹理的影响，发现珩磨过程中形成纹理有利于存储润滑油，除节圆位置外，两侧的纹理分别向反方向延伸。JOLIVET等[6-7]研究宏观和微观几何缺陷对振动的影响，开发了一级齿轮系统的二维有限元仿真模型，提出了区分磨齿和强力珩齿的影响单级直齿轮噪声的精加工工艺，但齿面微尺度粗糙度对齿轮噪声的影响尚未得到很好的研究和理解。韩江等[8]对内齿强力珩齿与蜗杆砂轮磨齿切削机理进行对比分析与试验研究，得出两种工艺对齿面几何精度的影响规律。SCHENK等[9]设计一种无需修整的高性能珩磨轮，分析了轴交角对切削速度的影响，以及中心距和轴交角对珩削齿面纹理分布的影响关系。AMINI等[10]通过实验证明了内啮合强力珩齿加工的齿轮表面形貌是一种弧线几何纹理，可以有效降低齿轮啮合传动噪声。任强等[11]研究了珩削速度和磨粒粒度等因素对齿面粗糙度的影响，建立了工件表面各点运动线速度方程，探究不同齿高处粗糙度变化规律。LI等[12]研究了不同工况下齿面形貌引起的时变摩擦系数对直齿圆柱齿轮动态特性的影响，结果表明该影响主要体现在齿面摩擦力方向上。

本文根据内啮合珩齿原理和空间曲面共轭啮合理论，建立珩齿加工过程运动模型和接触线模型，分析珩齿加工参数中心距和轴交角变化时珩磨轮与工件齿面接触点的相对运动速度大小和方向，通过接触点处珩削速度来模拟珩削轨迹，研究内啮合强力珩齿加工时工件齿面纹理的形成机制，建立珩削齿面纹理的预测模型，提出一种对珩齿齿面纹理的分布及变化趋势的主动控制方法，为齿轮优化设计及珩削加工提供理论依据。

1 内啮合强力珩齿工件齿面纹理形成机制

珩齿过程中，内齿珩磨轮与工件齿轮在空间上呈交错轴分布，在各自的电机驱动下，按一定的传动比保持强制性联动关系。内齿珩磨轮表面磨粒与工件齿轮齿面存在相对滑擦运动，并通过珩磨轮对工件齿轮齿面施加接触压力，使磨粒切入切出工件齿轮齿面，在工件齿面上留下一系列加工痕迹，最终形成齿面纹理。

由于工件齿轮与珩磨轮轴线间存在一夹角，珩轮与工件接触点处的珩削速度vC由齿向速度vL和齿形速度vH叠加而成(图1)：

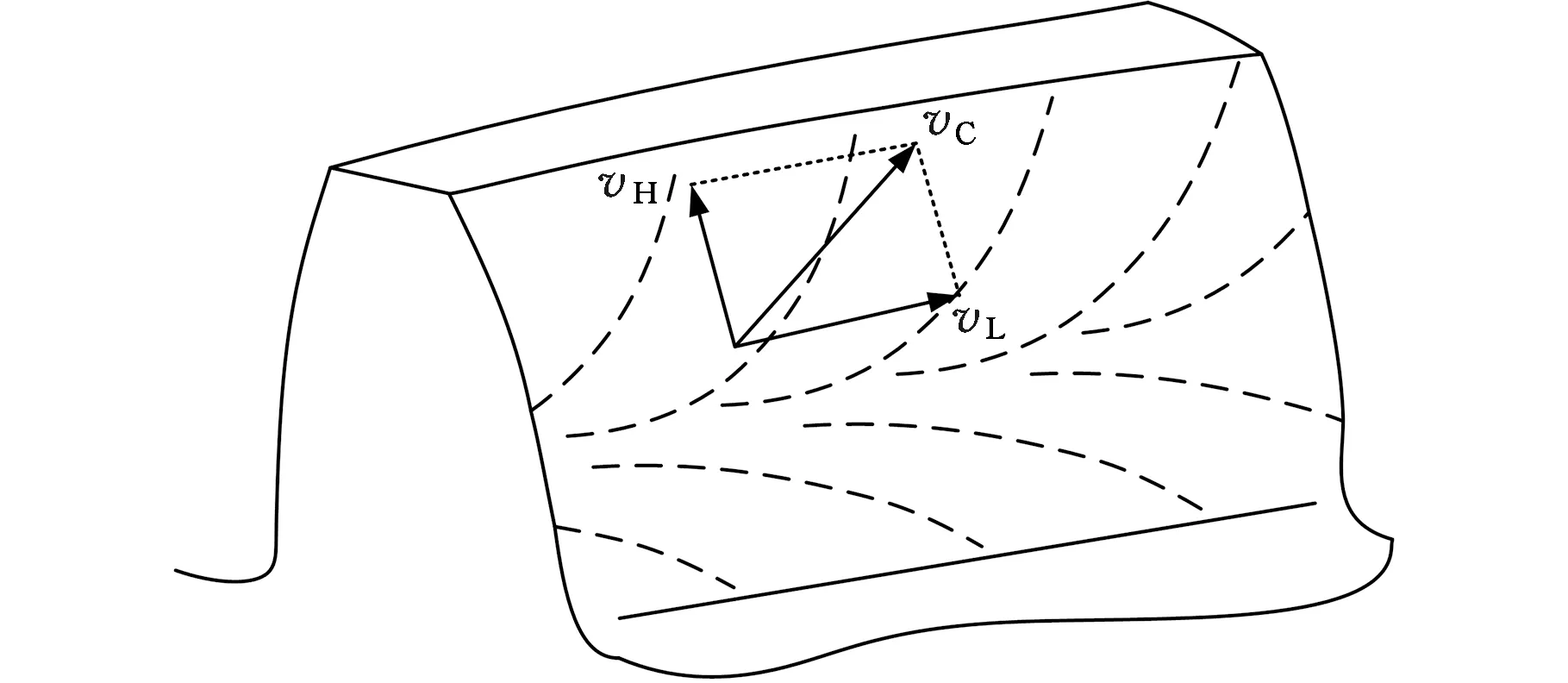
图1 内啮合强力珩齿工件齿面珩削速度Fig.1 Honing speed of gear surface during internal gearing power honing

vH=2π(ρWnW-ρHnH)

(1)

(2)

(3)

式中，ρW、ρH分别为工件齿轮与珩磨轮接触点处的垂直于轴线剖面中的曲率半径；nW、nH分别为工件齿轮与珩磨轮的工作转速；rW为工件齿轮上接触点到工件齿轮轴线的距离；Σ为工件齿轮与珩磨轮轴线的夹角(即轴交角)；βH为珩磨轮的螺旋角。

在工件节圆位置，齿形速度vH为零，在节圆两侧速度逐渐增大，方向相反，齿向速度vL与工件接触点到轴线的距离rW和珩磨轮螺旋角βH有关。因此在工件齿面上任意一点的珩削速度vC的大小和方向均不相同，这一特点使得珩削后的齿面纹理呈弧线。珩齿加工时工件与珩磨轮为线接触[13]，为研究工件齿面珩削纹理，需建立珩削时工件齿面接触线模型。

2 工件齿面接触线模型

珩齿加工时，工件齿面与珩磨轮齿面满足共轭啮合关系，通过建立工件与珩磨轮的空间坐标系和工件齿面数学方程，结合共轭啮合条件，对工件齿面接触线数学模型进行推导。

2.1 建立工件齿轮与珩磨轮空间坐标系

建立珩齿加工过程的空间坐标系，如图2所示。SW(OWxWyWzW)和SH(OHxHyHzH)分别为工件齿轮和珩磨轮的固定坐标系，S1(O1x1y1z1)和S2(O2x2y2z2)分别为工件齿轮和珩磨轮的运动坐标系，ω1和φ1为工件齿轮的运动角速度和转动角度，ω2和φ2为珩磨轮的运动角速度和转动角度，a为工件齿轮与珩磨轮的中心距。

图2 工件与珩磨轮空间坐标系Fig.2 Space coordinate system of workpiece and honing wheel

建立的运动坐标系间可以通过如下变换矩阵相互转换：

M12=M1WMWHMH2

(4)

其中,M12表示珩磨轮运动坐标系与工件运动坐标系的坐标变换关系，其他坐标变换矩阵以此类推。

2.2 建立工件齿轮数学模型

工件齿面是标准的渐开线螺旋面，渐开线沿工件的螺旋线旋转得到，建立工件齿面方程：

(5)

式中，rb1为工件齿轮基圆半径；σ0为工件齿面渐开线起始角；θ为螺旋线增量角；λ为渐开线增量角；p为螺旋线参数。

2.3 建立工件齿面接触线模型

珩磨轮齿面由与工件齿轮相同参数的标准金刚修整轮包络形成，因此与工件齿面为一对交错轴空间共轭啮合曲面，齿面接触点的相对运动速度v12与该点处的法向量n满足共轭啮合条件[14]，即相对运动速度方向与曲面法向量相互垂直：

v12n=0

(6)

工件与珩磨轮接触点处的相对运动速度需在同一参考坐标系下计算，此处以工件固定坐标系SW(OWxWyWzW)为参考分析，得到在任意接触点的相对运动速度公式:

v12=ωWrW-ωHrH

(7)

式中，ωW和ωH分别为工件齿轮和珩轮接触点在工件固定坐标系SW下的角速度矢量;rW和rH分别为工件齿轮和珩轮接触点在工件固定坐标系SW下的位置矢量。

工件齿轮接触点的法向量与齿面垂直:

(8)

rW=MW1r1

珩轮与工件齿轮在啮合相邻两面为线接触。在同一时刻，工件齿面上所有满足共轭啮合条件的点的集合构成该啮合瞬间对应的接触线。接触线方程可用下式表示:

(9)

式中，i12为工件齿轮与衍磨轮的传动比。

将工件齿面从开始啮入到啮出过程转过的角度等分，可得到齿面上多条接触线。沿齿宽方向等距取点，以该点的珩削速度方向为纹理方向，可以得到图3所示的工件齿面珩削纹路模型。

图3 工件齿面珩削纹路模型Fig.3 Honing texture model of workpiece gear surface

3 珩磨轮修整对珩齿加工参数的影响

在珩齿加工过程中，珩磨轮会发生磨损，为了使磨钝后的珩磨轮重新获得加工能力，需要对其进行修整，使其表面露出新的磨粒。常用的珩磨轮修整工艺主要有两种：定轴交角修整和变轴交角修整。采用定轴交角修整珩磨轮时，金刚修整轮只做径向进给运动将珩磨轮表面材料去除；采用变轴交角修整珩磨轮时，在金刚轮做径向进给运动的同时，通过附加珩磨头摆动来调整珩磨轮的螺旋角，大致修整过程如图4所示。

图4 珩磨轮修整示意图Fig.4 Schematic diagram of honing wheel dressing

变轴交角修整工艺可以增加珩磨轮修整次数，延长使用寿命。将轴交角作为中心距的函数，在对珩轮进行径向修整的同时轴交角也随之改变，改变后的轴交角Σ′函数关系如下:

(10)

式中，ω1、r01和β01分别为工件齿轮的角速度、珩削时的节圆半径和螺旋角；ω2为珩磨轮的角速度；Δa为珩磨轮的径向修整量，即中心距a的变化量。

无论是定轴交角修整还是变轴交角修整，在修整后珩磨轮的中心距和轴交角均会发生改变，会对加工出的齿轮质量产生影响。在实际生产过程中，珩磨轮在加工同一批齿轮时可能要经历多次修整，调整加工参数以保证珩削质量稳定对实际生产加工具有重要意义。

4 珩削速度的影响因素分析和珩削纹理预测与控制方法

根据接触点速度式(3)，珩轮与工件的轴交角Σ和中心距a对齿面接触点的相对运动速度的大小和方向有影响。以齿轮端面处的一条渐开线为研究对象，分析珩磨轮修整过程中，从齿根到齿顶相对运动速度的变化规律。

4.1 加工参数对珩削速度大小的影响

对珩磨轮进行修整以调整珩磨轮与工件间的加工参数，在不同的加工条件下加工相同参数的工件，参数如表1所示。得到相应的相对运动速度曲线，如图5所示。

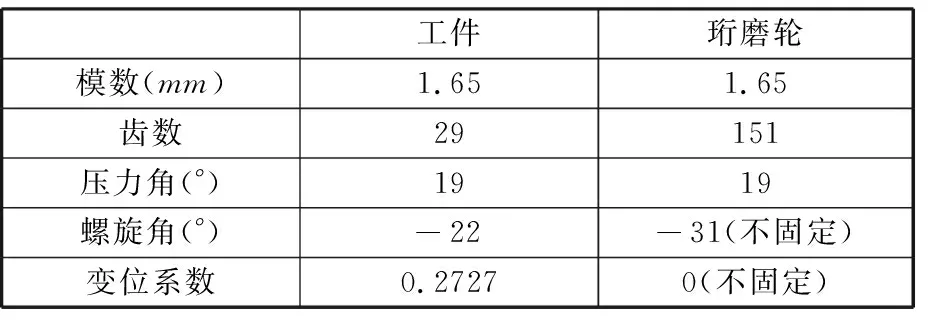
表1 工件与珩磨轮基本参数Tab.1 Basic parameters of workpiece and honing wheel

(a)改变中心距

(b)改变中心距和轴交角图5 不同加工参数对相对运动速度大小的影响Fig.5 Influence of different machining parameters on the magnitude of honing speed

当仅对珩磨轮进行径向修整以改变珩轮与工件齿轮的中心距a时，接触点的相对运动速度如图5a所示。随着珩磨轮的修整，中心距a不断增大，整个渐开线上的相对运动速度发生较大改变，速度最小位置点不断向齿顶方向移动，且从齿根到齿顶的速度差值不断增大。珩削速度的大小对齿面加工质量有重要影响，速度的增大有利于珩齿加工时材料的去除，可以减小珩削力，增加珩削过程的稳定性，有助于获得更好的表面加工质量。但较大的速度变化会导致加工过程中珩削力发生周期性变化，这种激励会被机床结构放大，从而对加工过程造成破坏[15]。随着珩轮修整量的增大，中心距变大，所加工工件齿轮在齿顶处的加工质量比齿根位置低，齿面精度不均匀，易造成齿轮工作不稳定。

对珩磨轮进行修整同时改变珩轮与工件齿轮的中心距a和轴交角Σ，轴交角与中心距满足函数关系式(10)，接触点的相对运动速度如图5b所示。随着珩磨轮的修整，整个渐开线上的相对运动速度增大, 从齿根到齿顶的速度差值不断减小，且速度最小位置点基本不变。此时改变加工参数后，在提高珩削速度的同时还减小了速度差，有利于珩削过程的稳定进行，获得较好的加工质量，延长珩轮的使用寿命。

4.2 加工参数对珩削速度方向的影响

珩削后工件齿面加工纹理由大量的微小加工痕迹构成，加工痕迹的方向由珩削速度的方向决定。改变珩轮与工件的中心距与轴交角等加工参数，珩削速度的方向也会发生改变，使工件加工纹理发生变化。

对比不同参数下的珩削速度矢量，如图6所示，箭头方向表示速度方向，长度表示速度大小，当速度矢量竖直向下时代表该点只有齿形速度，而齿向速度为零，即该点为节点。图6a所示为改变中心距时齿轮端面渐开线上的珩削速度矢量，随着修整量Δa的增大，工件齿轮的加工节圆位置向齿顶方向移动，各点速度方向不断变化，修整前后工件齿面加工纹理发生显著变化。图6b所示为同时改变中心距和轴交角时齿轮端面渐开线上的珩削速度矢量，工件节圆位置基本保持恒定，各点速度方向变化较小，齿面加工纹理变化最小。这一规律对实际的齿轮珩削生产加工具有重要意义，能够保证在不同加工参数下达到相同的效果，可以用于珩磨轮的修整工艺。

(a)改变中心距

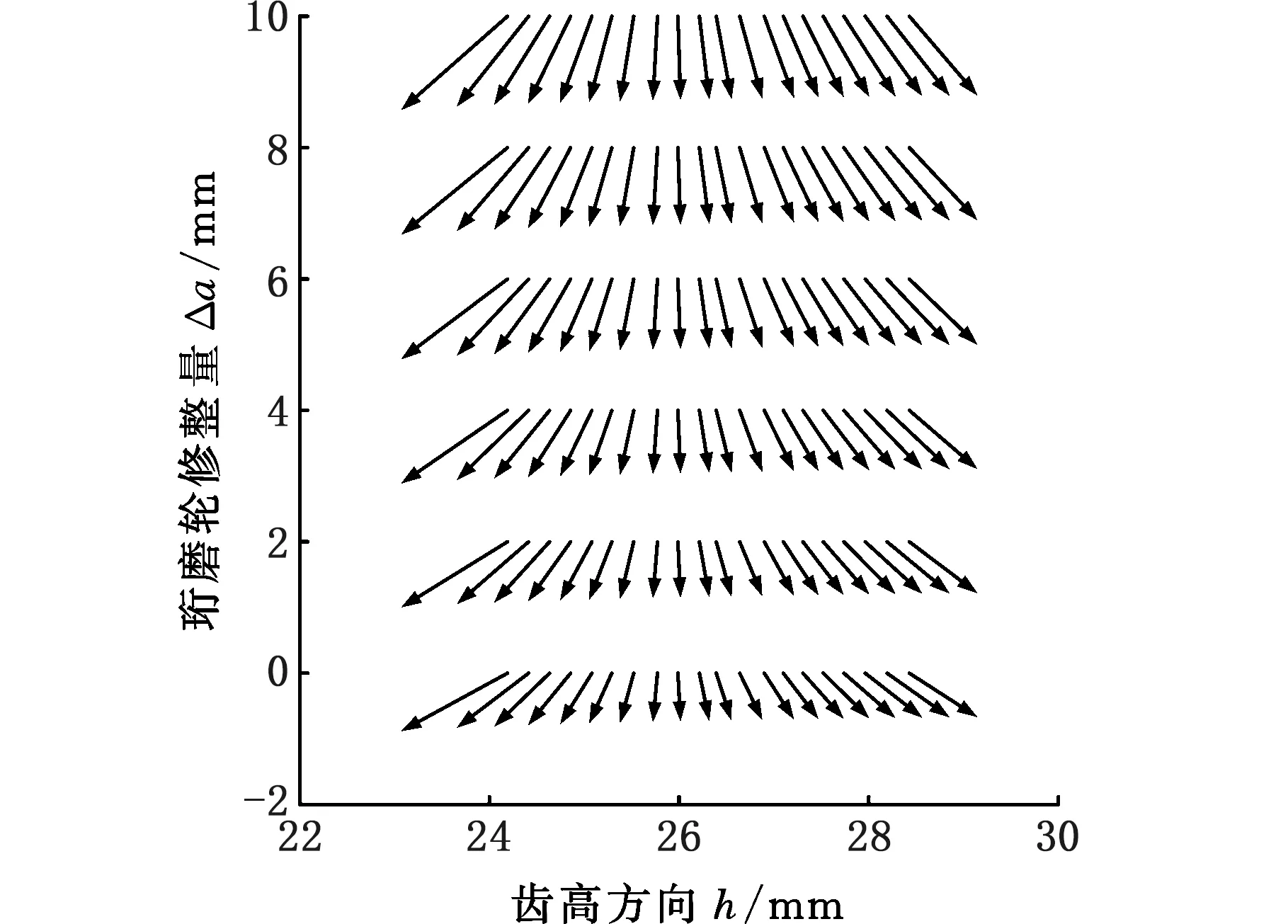
(b)改变中心距和轴交角图6 不同加工参数对相对运动速度方向的影响Fig.6 Influence of different machining parameters on the direction of honing speed

4.3 珩齿工件齿面纹理主动控制的实现

调整珩轮与工件齿轮的轴交角和中心距大小，不仅可以改变加工时齿轮节圆位置，还能够控制珩削速度方向的变化，得到不同的齿面纹理。为了描述这一变化，绘制了加工后有效齿根圆处纹理与齿向的夹角示意图，见图7。图中路径①代表仅调整珩轮与工件中心距而轴交角不变的过程，通过对珩轮进行径向修整来实现。增大中心距可以使加工时工件节圆位置向齿顶方向移动，并且减小齿面加工纹理的曲率，使齿面纹理向齿廓方向靠近。路径②代表同时改变中心距和轴交角的过程，通过在珩轮修整时同时对中心距和轴交角进行微量调整来实现。这种方法可以在改变参数后，使工件的加工节圆位置保持恒定，齿面珩削轨迹大致趋势基本不变，加工纹理的变化最小。

图7 中心距与轴交角对珩削纹理的影响Fig.7 Effect of center distance and crossed axes angle on honing texture

在某一加工参数下，如图7中O点，改变珩磨轮的螺旋角βH可以调整工件与珩轮的轴交角Σ，保持中心距a不变，可以使O点沿轴交角方向移动；改变珩轮的变位系数xH可以调整工件与珩轮的中心距a，保持轴交角Σ不变，可以使O点沿中心距方向移动。基于此方法，通过合理选择珩轮的螺旋角和变位系数，可以使位置点O在区域内移动，得到任意所需的加工纹理。

5 实验验证

采用不同的加工参数对相同参数的齿轮进行实际齿轮加工，工件与珩磨轮基本参数如表2所示。加工机床型号为Fässler HMX-400，加工方式为内啮合强力珩齿，加工出的齿轮工件如图8所示。

表2 实验工件与珩磨轮基本参数Tab.2 Basic parameters of workpiece and honing wheel in experiments

图8 加工齿轮工件Fig.8 Machined gear workpiece

采用显微镜(EX30)对齿轮的左右齿面进行检测，由于空间限制，观察区域限定在分度圆与齿顶之间。

表3所示为不同加工参数下珩削工件齿轮齿面纹理预测模型与实际齿面形貌三维检测结果。齿轮珩削加工纹理均呈弧线形，在不同加工参数下珩削纹理的分布和形状不同。在轴交角Σ为8°、中心距a为118 mm时，珩削齿面纹理预测模型中，齿顶处纹理与齿向的夹角为49°，按该参数加工的齿轮表面纹理走势与红线一致，在齿顶位置处夹角为50°，与预测结果相差1°，误差为2.0%；在轴交角Σ为13.9°、中心距a为128 mm时，珩削齿面纹理预测模型中，齿顶处纹理与齿向的夹角为30°，实验齿轮表面纹理走势与红线一致，在齿顶位置处夹角为31°，与预测结果相差1°，误差为3.3%。在误差允许范围内，不同加工参数下实际齿轮加工纹理与纹理预测模型基本一致，验证了预测模型与控制方法的准确性。