一种针对圆锥体外表面贴装的机械手设计分析与优化

何宇凡 孙江宏,2 高 锋 李乃峥 何雪萍 王军见

1.北京信息科技大学机电工程学院，北京，100192 2.清华大学机械电子工程研究所，北京，100084 3.中国机械科学研究总院集团，北京，100044 4.国家机床质量监督检测中心，北京，100102

0 引言

贴装源于SMT(surface mounted technology)，最初应用在航空航天领域，流行于电子组装行业。贴装技术可以参考贴片机设备，通过吸取、检测、定位和贴装等动作配合将元器件安装于PCB(printed circuit board)表面[1]。贴装技术发展历经数十载已经得到长足的进步，机构原理和工作方式已趋于稳定，目前研究主要集中在优化部件配合进而提高贴装效率以及算法预测贴装性能从而提高贴装质量[2-3]。针对以获得最小周期时间为目标的线平衡问题[4-7]， HE等[8]提出一种分层启发式方法平衡多台相同设备间工作量，周期时间降低了6.94%。PARK等[9]提出一种用于多头表面贴装机的装配规划方法，通过将动态规划技术应用于馈线布置优化和布局顺序优化，最终缩短装配时间。王君等[10]基于改进蚁群算法对贴装过程进行优化，276个、44种元器件的贴装效率提高了6.45%。近年来人们利用设备信号来监测、预测贴装过程，采用的方法有离散小波变换(DWT)[11]、二代小波变换(SGWT)[12]、循环谱分析[13]和经验模态分解(EMD)[14]等。WANG等[3]采用三维双树复小波变换及递归神经网络对低噪干扰下的性能预测进行建模，可有效预测工作过程性能。自然界中也存在类似贴装的动作，生物通过进化出吸盘实现对复杂曲面的吸附及攀登，如壁虎吸附立面、树蛙吸附树枝干、鱼类吸附其他鱼类以及贝类吸附礁石等[15-24]。FLAMMANG等[25]针对鱼吸附功能进行研究，发现鱼在颅静脉的加压作用下，利用椎间盘吸盘器官实现对不同粗糙度表面的长期可逆附着。WANG等[26]借鉴鱼吸附大鱼的椎间盘器官研制出的仿生机器人具有抗拉脱、抗横向摩擦的特点，在空气中及水中均有良好吸取能力。KIM[27]对可吸附复杂立面实现生长的常春藤进行研究，发现枝条与墙壁接触后，通过表皮转化、黏合剂分泌、细胞分裂改变枝条质地从而提高附着位置机械强度，进而获得最大吸附性能。

对以圆锥体为代表的空间复杂曲面进行表面贴装成为热点及难点。如导弹头部贴装抗高温陶瓷防爆膜片、锥顶造型建筑表面贴装隔热薄膜等技术环节，多采用专用贴装设备及人工操作，拓展性及贴装效率难以保证。针对上述难点研发通用自动化装备可有效解决问题。SMT技术的应用对象为平面结构，自然界吸附多为生理结构而非机械结构，因此圆锥体外表面贴装方案设计可采用SMT技术要求并参考自然界动植物对复杂曲面吸附的实例。

本文设计出一种圆锥体外表面贴装机械手，作为串联式机械臂的末端执行器。通过空间分析确定圆锥体几何特征及贴装方式，建立工作机构动力学、运动学方程，利用遗传算法NSGA-Ⅱ得出最佳结构尺寸值，最后通过样机实验验证机械手可行并得出最佳工作控制方案。

1 空间分析及构型设计

1.1 空间分析

图1a为圆锥体三维示意图，圆锥体横截面半径沿z轴方向线性变化，因此贴装于圆锥体外表面的膜片上弧和下弧也沿z轴方向线性变化。图1b红色部分为贴装膜片机械手单次完整贴装流程的工作空间，通过设计机械手自上而下对圆锥体外表面进行膜片分次贴装实现1/4圆锥体外表面贴装工作。

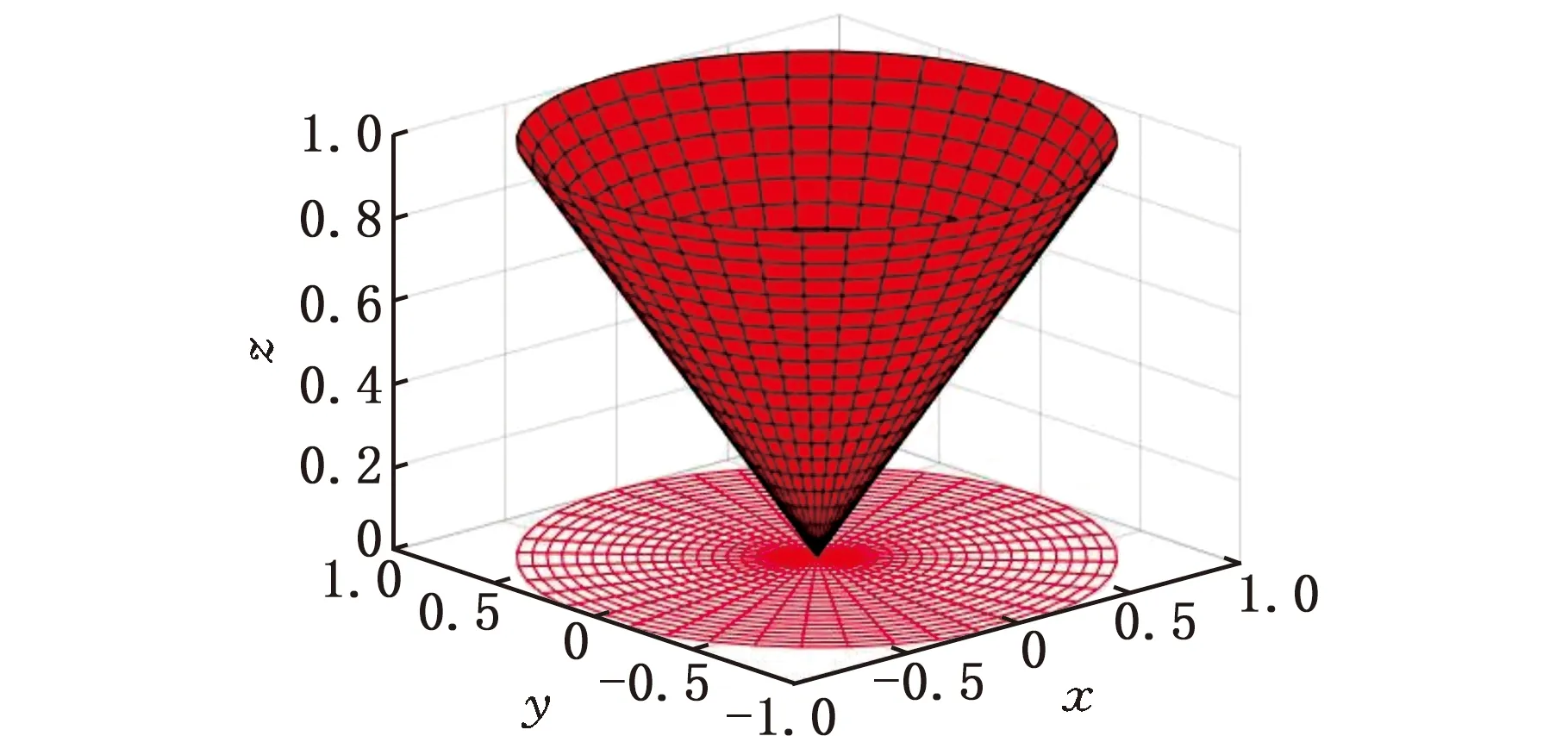
(a)圆锥体三维示意图

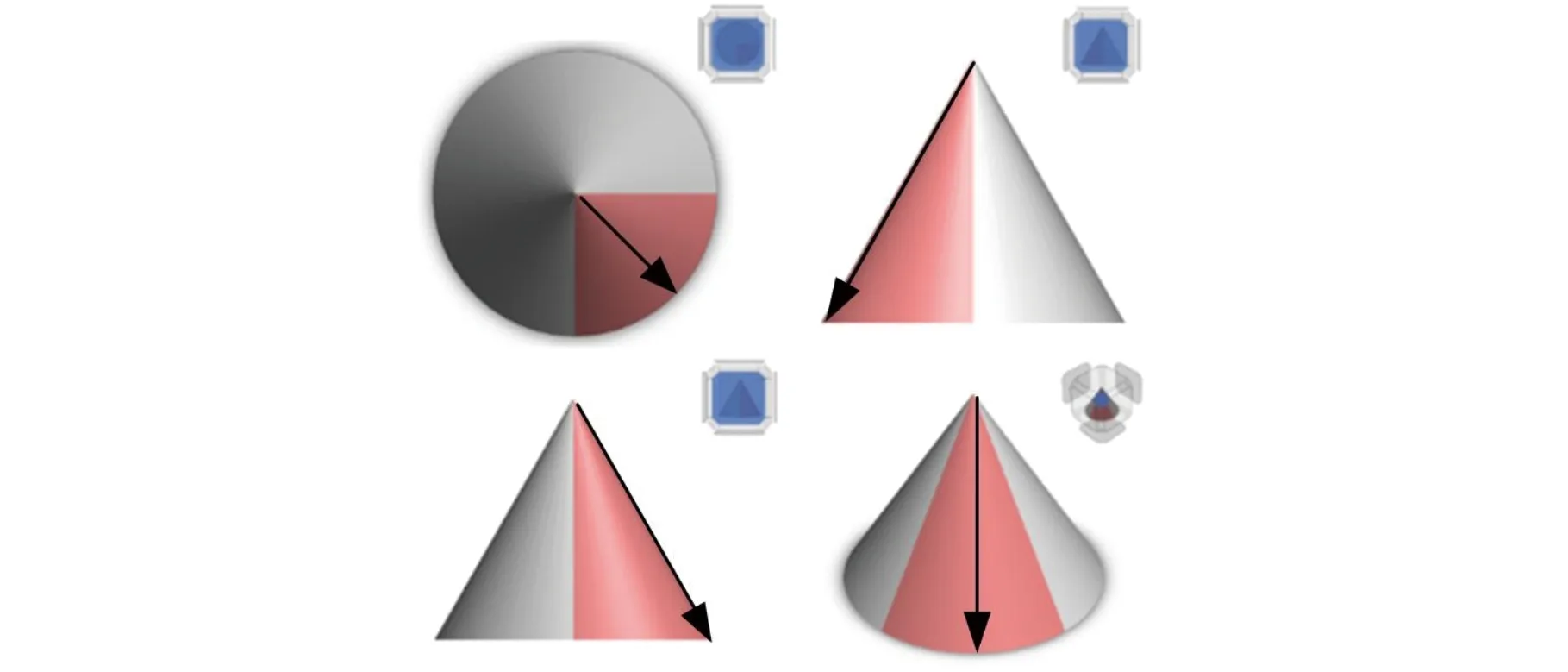
(b)单次贴装空间图1 贴装工作空间Fig.1 Workplace of mounting

1.2 构型设计

根据工作动作要求提出一种新型末端机械手构型，通过6个移动副配合连杆机构实现。如图2所示，移动副1中滑块上固接有一根连杆作为移动副2的滑动轴，移动副2中滑块固接有一根连杆作为移动副3中的滑动轴，移动副3与移动副4中的滑块通过连杆固接，移动副5、移动副6为移动副3、移动副4的对称结构。移动副1中滑块竖直运动即可带动移动副2、3、4、5、6中滑块运动，其中移动副4、6中滑块运动空间角度可根据机构设计进行调整。

图2 机械手构型简图Fig.2 Schematic diagram of manipulator configuration

根据修正G-K公式可对空间机构自由度进行求解：

式中，M为自由度数；d为系统阶数；n为构件数；g为运动副个数；fi为第i个运动副的自由度数；v为冗余约束个数；ζ为局部自由度。

由图2可知，移动副5、6为移动副3、4的对称结构，对机构运动无额外影响，因此仅分析移动副1、2、3、4组成的运动链，d为3，n为4，g为4，f为4，v为0，ζ为0，算得自由度M为1。

2 结构设计及理论分析

2.1 结构工作原理

根据构型设计建立末端机械手结构三维实体。如图3所示，机械手空间结构通过6个移动副实现。连接模块2可沿丝杠滑块延伸出的两根轴滑动，光轴7一端与连接模块2固接，吸盘模块3分别与光轴7和圆锥体母线方向导向轴6进行轴孔配合，定位架4与支承架8固接并最终连接在丝杠基座。控制丝杠滑块沿丝杠轴上下移动，动作将经由连接模块2、光轴7传导至被光轴7和圆锥体母线方向导向轴6限制自由度的吸盘模块3，使其最终沿圆锥体母线方向导向轴6上下滑动，实现图4所示曲面包覆变构，进而实现将各圆锥体高度对应的膜片传送至正确位置并最终通过吸盘模块吸取压强变化完成贴装。

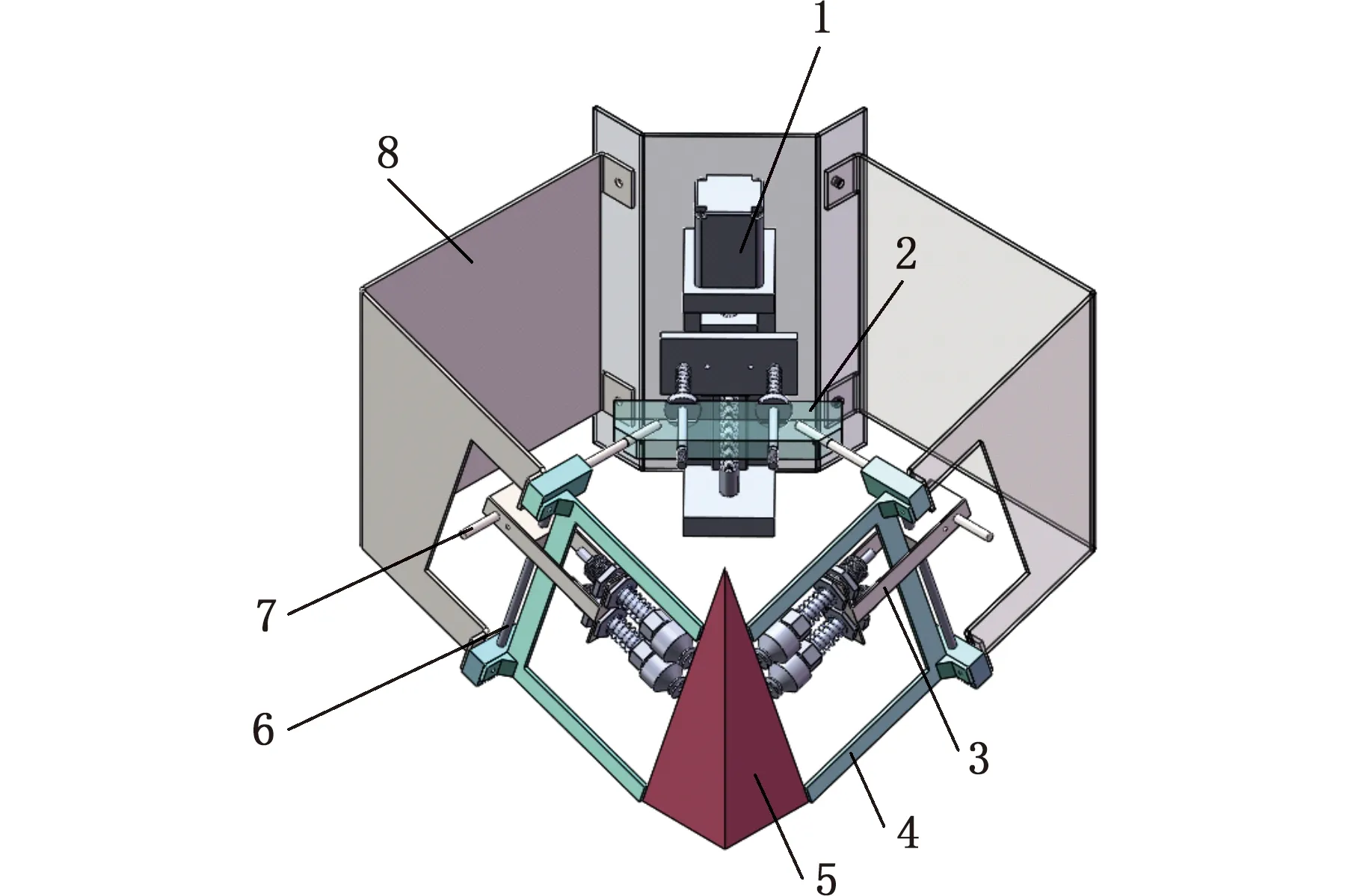
1.驱动丝杠 2.连接模块 3.吸盘模块 4.定位架 5.1/4圆锥 6.圆锥体母线方向导向轴 7.光轴 8.支承架图3 机械手结构示意图Fig.3 Structural diagram

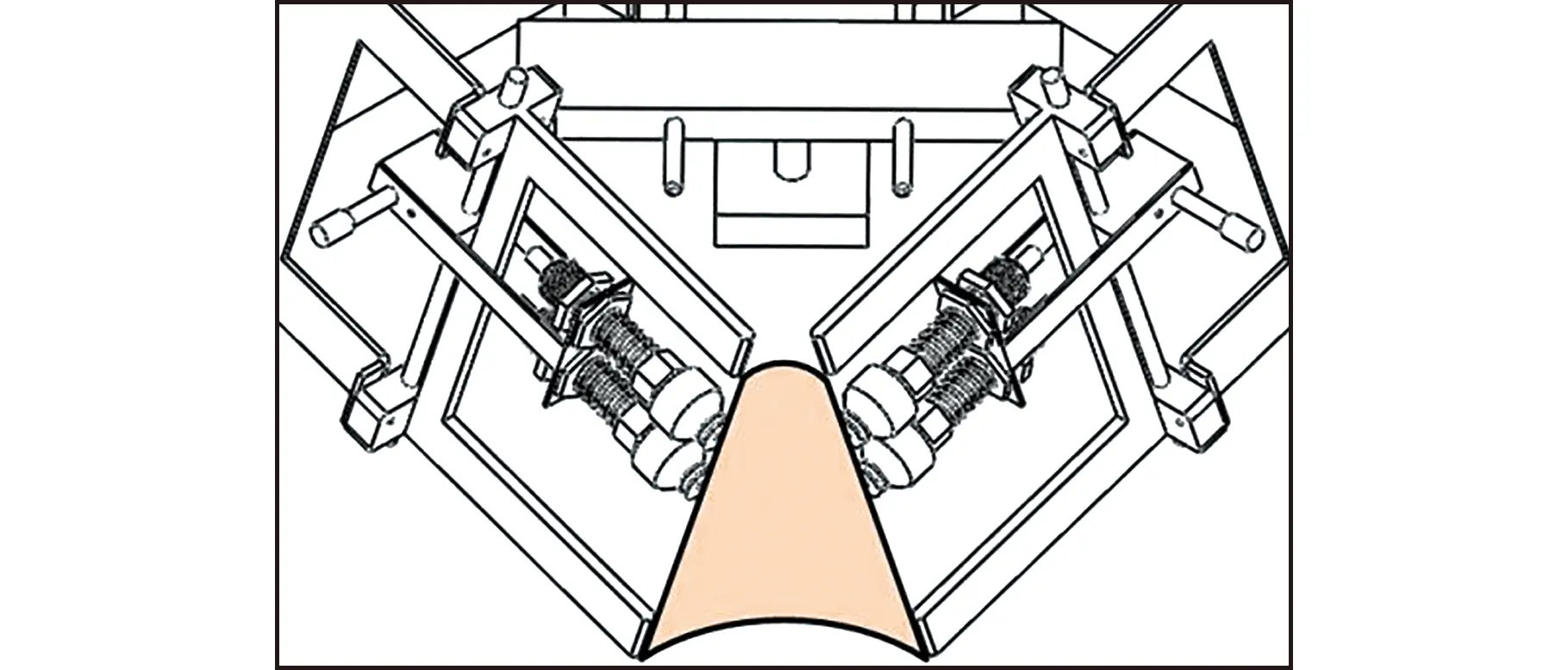
图4 机械手工作末端Fig.4 Manipulator end

此种单自由度构型机械手的优势如下：①精度高，不涉及多电机配合误差；②适用性强，驱动简单，可满足极端使用工况；③互换性强，模块化结构易于运维。

2.2 基于拉格朗日法的动力学分析

根据拉格朗日法构建动力学方程，如图5所示：质点1为丝杠滑块，质点2为连接模块，质点3与4为连接块且相互对称，因此图中只保留质点3实体。

图5 动力学分析模型Fig.5 Dynamic analysis model

首先建立质点1、2、3、4的坐标描述:

x1=0
y1=0
z1=-d1x2=0
y2=-d2
z2=-d1
x3=-a-d3cosθ1
y3=-d2-d3sinθ1
z3=-d1-bsinθ2
x4=a+d3cosθ1
y4=y3=-d2-d3sinθ1
z4=z3=-d1-bsinθ2

求得各质点速度的平方：

进而可表达出系统动能:

式中，mi(i=1,2,3,4)为质点i的质量。

系统势能如下：

最终可得到拉格朗日函数及动力学方程表达如下：

根据动力学方程可知，机械手运动系统仅受外界输入加速度及自身重力作用。

2.3 基于D-H法的运动学分析

根据D-H坐标建系原则可得到机械手单侧坐标变换，如图6所示，D-H参数如表1所示，进而可对机构进行正逆运动学求解。

图6 机构D-H坐标系Fig.6 D-H coordinate of device

表1 机构D-H参数表Tab.1 D-H parameter of device

根据建立的D-H坐标系及参数表可对机构由起始坐标系({0}系)至末端坐标系({4}系)进行表达。采用左乘方法，{0}坐标系沿Y轴平移-d1，并绕X轴旋转α0，得到{1}坐标系；{1}坐标系沿Z轴平移-d2，并绕Z轴旋转θ2，绕Y轴旋转α1，得到{2}坐标系；{2}坐标系沿Z轴平移d3，并绕Y轴旋转θ3，绕X轴旋转α2，绕Z轴旋转18.85°，得到{3}坐标系。转换矩阵T表达式为

(1)

代入机械手结构尺寸参数可得

nx=-0.23ox=0.71ax=0
px=0.67d3-0.71d2
ny=-0.23oy=-0.71ay=0
py=0.71d2+0.67d3
nz=0.95oz=0az=0
pz=0.32d3-d1

图7 工作空间曲面Fig.7 Workspace surface

3 基于遗传算法NSGA-Ⅱ的多目标优化

针对单一参量进行优化可根据分析目标函数寻求最优解，而针对多参量的优化往往具有多目标函数，且各目标函数中均含有待优化参量，因此需采用优化算法筛选出最优解集。遗传算法NSGA-Ⅱ具有计算数据量小、寻优过程简单、全局寻优能力强的特点，因此本文将采用此算法进行多目标优化。

3.1 建立目标函数

由机械手运动及受力分析可知，光轴作为中间传动零部件是全局最大负载零件，需对其进行多目标优化进而确定满足工作条件的最优结构尺寸。优化参数分别为光轴半径r和光轴长度l，约束边界条件分别为

5 mm≥r≥2 mm120 mm≥l+20≥70 mm

为保证光轴在满足强度、刚度要求的同时体积最小，目标函数设定为光轴弯曲应力σ和体积V表达式：

f2(x)=V=r2l

式中，M(t)为弯矩；W为挠度。

3.2 优化过程及结果

在MATLAB环境下搭建NSGA-Ⅱ算法架构，设置求解参数如表2所示。求解得到f1(x)和f2(x)收敛过程如图8所示，收敛均在20代开始趋于稳定，最终得最小弯曲应力0.002 MPa、最小体积280 mm3。对收敛过程量进行筛选可得到Pareto最优解平面，根据本文优化目标，选取图9蓝色线框内的解作为最终优化结果。在优化过程量中找到最优解对应的优化参数值，如表3所示，最终选取r=2 mm、L=70 mm作为光轴结构尺寸优化结果。

表2 计算求解参数Tab.2 Solution parameter

(a)f1(x)

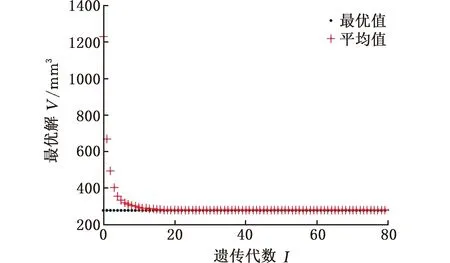
(b)f2(x)图8 目标函数收敛过程Fig.8 Convergence of objective function

图9 Pareto最优解平面f1(x)-f2(x)Fig.9 Pareto optimal solution plane f1(x)-f2(x)

表3 优化过程Tab.3 Optimization process

光轴优化前后分别施加工作载荷并进行静力学分析，得到形变、应力对比结果。如图10a所示，优化后光轴沿轴向长度形变增幅相较于优化前减小，且最大形变由0.98 mm减小为0.451 mm，最大形变量减小了54.0%。如图10b所示，优化后光轴沿轴向长度应力曲线斜率相较于优化前相近但幅值明显减小，最大应力由121 MPa减小为91 MPa，最大应力值减小了24.8%。

(a)形变对比

(b)应力对比图10 优化前后对比Fig.10 Comparison before and after optimization

4 动态性能仿真及实验对照

根据优化结果重新建立机械手模型并搭建实验台，将动力学仿真分析结果与实验结果进行比对，验证机械手的可行性。

4.1 理论模型仿真分析

ADAMS环境下的动力学分析如图11所示，机械手简化为5部分，丝杠轴1与丝杠滑块2之间、丝杠滑块2与连接块3之间、连接块3与吸盘模块4之间、吸盘模块4与吸盘模块导向轴5之间为移动副，在丝杠轴1与丝杠滑块2的移动副处驱动，其余移动副为自由状态。

1.丝杠轴 2.丝杠滑块 3.连接块 4.吸盘模块5.吸盘模块导向轴图11 机构简化模型Fig.11 Simplified device model

设丝杠运动满足理想驱动控制函数step(time,0,0,0.1,step(time,0.1,0.05,0.9,step(time,0.9,0.05,1,0)))，对虚拟样机进行仿真分析得到丝杠滑块(吸盘模块Y方向分量)位移、速度和加速度的绝对值变化如图12所示：位移量变化平稳，速度在0.1 s内增至0.05mm/s，随后保持0.9 s并于0.1 s内减速至零，启动时刻及停止时刻产生0.6 mm/s2的加速度突变，中间无加速度产生。

图12 仿真位移、速度、加速度变化Fig.12 Simulation of position, velocity and acceleration

4.2 样机试验台对照

搭建样机实验平台如图13所示。装置样机的丝杠滑块及吸盘末端分别安装有加速度传感器，由PC通过蓝牙对其进行数据采集；220 V交流电源对直流电源与控制器供电，直流电源为驱动器供电；驱动器对装置样机电机输入脉冲实现电机旋转运动，其中脉冲值为电机转动一周所需电子齿轮比，可在400～25 000之间进行设置；控制器由220 V交流电源供电，可设置输入给驱动器的单次脉冲值，进而控制装置样机丝杠滑块单次移动距离。

图13 样机控制示意图Fig.13 Prototype control diagram

分别取电机驱动脉冲值为800、1600，输入脉冲值分别为驱动脉冲值的1～5倍进行实验，如表4所示。采集得到机械手加速度变化，利用经验模态分解法(EMD)去除噪声后得到曲线，其中图14a、图14b为驱动脉冲800、输入脉冲800～4000情况下丝杠滑块和吸盘末端加速度变化，图15a、图15b为驱动脉冲1600、输入脉冲1600～8000情况下丝杠滑块和吸盘末端加速度变化。以驱动脉冲800、输入脉冲1600为例进行分析，记作“800～1600”，其他同理。分析结果可知，丝杠滑块在启动和停止时刻产生加速度最大值与最小值，运行中加速度随电机转动呈周期性变化。吸盘末端在启动和停止时刻加速度变化响应时间短，由于运动经多零部件传递产生加速度振荡，并于10 ms内稳定于±0.1 cm/s2内。驱动脉冲1600相较于驱动脉冲800电机具有更高的电子齿轮比，运动平顺性能更好，驱动近端加速度变化更具规律性，驱动远端加速度相应性能和变化幅值相近。

表4 驱动、输入脉冲值Tab.4 Drive and input pulse value

(a)驱动脉冲为800丝杠滑块加速度

(b)驱动脉冲为800吸盘末端加速度图14 丝杠滑块、吸盘末端加速度(驱动脉冲值为800)Fig.14 Acceleration of screw slider and end of vacuum chuck(driving pulse is as 800)

(a)驱动脉冲为1600丝杠滑块加速度

(b)驱动脉冲为1600吸盘末端加速度图15 丝杠滑块、吸盘末端加速度(驱动脉冲值为1600)Fig.15 Acceleration of screw slider and end of vacuum chuck(driving pulse is as 1600)

丝杠滑块样机运动过程中仅受电机加速度及自身重力作用可验证2.3节理论推导，样机相较于仿真实验加速度变化趋势相同，但由于驱动电机转动产生周期性加速度变化导致中间理论匀速段相异。吸盘模块为机械手末端，运动传递经过多个零件会产生振动累加，由于样机采用304不锈钢材质加工，因此表现出加速度幅值较小，若进一步抑制加速度振荡幅值需增设支撑梁、连接柱等结构件。

4.3 样机性能

利用样机进行圆锥体外表面贴装。如图16所示，操作驱动丝杠使吸盘模块沿圆锥体母线方向导向轴上下平移并进行贴装实验：①使吸盘模块运动到指定贴装位置；②接通气泵及负压发生器，使吸盘拾取贴装膜片；③机械手贴合于圆锥体外表面，使膜片实现贴装；④切断气泵完成贴装，机械手脱离圆锥体；⑤更换吸盘模块贴装位置并再次完成①～④操作。

(a)第一位置 (b)第二位置

(c)第三位置 (d)第四位置图16 机械手贴装实验图Fig.16 Experiment of manipulator mounting

贴装实验过程中，机械手可完成圆锥体各高度位置对应的外表面贴装。其中吸盘模块平移运动平顺稳定，吸盘对膜片的拾取精准牢固，对一侧涂有胶的膜片进行贴装时能够准确找到贴装位置，贴装效果如图17所示：膜片贴装平整、与圆锥体外表面接触均匀、边角无起翘现象发生。因此经实验验证，本文设计的针对圆锥体外表面贴装的末端机械手具有可行性。

(a)第一位置 (b)第二位置

(c)第三位置 (d)第四位置图17 贴装效果Fig.17 Effect of mounting

5 结论

本文通过对圆锥体进行几何特征分析，设计出一种针对圆锥体外表面贴装的串联机械臂末端机械手。根据贴装动作建立了机械手三维模型并分别进行构型分析、动力学分析和运动学分析。利用遗传算法NSGA-Ⅱ对零部件结构尺寸优化，结果表明,相较于优化前，优化后部件各位置应力降低10 MPa,最大应变降低62.5%。对比虚拟样机和样机动态性能实验，运动始末加速度变化趋势基本吻合，但由于电机特性导致运动过程中会存在周期性加速度变化。单独分析样机实验数据发现，驱动源伺服电机在高驱动脉冲条件下更具运动平顺性且加速度变化更具规律性。

本文主要贡献如下：

(1)提出一种针对圆锥体外表面贴装的串联机械臂末端机械手新构型。通过电机驱动可实现适应圆锥体不同高度下外表面贴装的变构，本文设计为目前首个应用于空间贴装的集成机械手结构，可简化现有贴装工作流程并降低工作难度，同时为后续相关研究奠定基础并提供思路。

(2)提出一套完整、可复制的设计、分析、优化流程。本文根据对贴装对象的分析进行结构的初步确定，通过构型分析、动力学分析和运动学分析建立理论分析模型并验证设计可行性，最后利用遗传算法对结构进行优化，并经生产样机验证所设计机械手稳定可行,为结构设计类型研究提供参考方案。

(3)根据虚拟样机和样机实验分析的对比结果发现,驱动源电机会对执行器加速度变化产生影响。在零部件静、动力学分析过程中,尤其是细长尺寸杆件、支撑件需考虑驱动源作用，并可将驱动电机对零部件的影响程度作为选取驱动电机的标准和依据。