考虑主轴-刀柄结合面特性的机器人铣削系统刀尖频响预测研究
2023-01-16梁志强石贵红杜宇超叶玉玲籍永建陈司晨仇天阳刘志兵周天丰王西彬
梁志强 石贵红 杜宇超 叶玉玲 籍永建 陈司晨仇天阳 刘志兵 周天丰 王西彬
1.北京理工大学先进加工技术国防重点学科实验室,北京,100081 2.北京神工科技有限公司,北京,100013 3.北京信息科技大学机电系统测控北京市重点实验室,北京,100192
0 引言
工业机器人由于其灵活性、智能性、经济性等优势而被广泛应用于大型复杂结构件的加工。然而,由于机器人开链式多自由度的结构特点,导致其刚性与机床相比相差将近两个数量级[1],铣削过程极易产生颤振,严重降低了加工表面质量与精度。理论推导机器人铣削稳定性叶瓣图是对机器人铣削稳定性控制的一种有效方式[2],其关键是对机器人铣削系统刀尖频响函数的准确获取[3-5]。由于机器人刀尖频响函数的位姿依赖性,如何在变位姿下准确获取机器人刀尖频响函数,成为机器人铣削领域研究的热点和难点。
目前用于获取加工系统频响函数的方法主要有模态实验法、子结构响应耦合法(receptance coupling substructure analysis, RCSA)[5-6]与基于实验的有限元分析法[7-8]。2000年,SCHMITZ等[9]推导出了装配体频响与各子结构频响的函数关系,首次提出了子结构响应耦合方法。随后的研究者将该方法用于机床频响计算、结合部建模与刀尖频响预测。李宇庭[3]运用子结构耦合方法结合模态实验建立了机器人刀尖频响预测模型,并通过实验验证了其准确性。不过加工系统子结构之间的连接状态模型和连接参数的辨识一直是该方法的难题,辨识方法还处于研究阶段,距离工程应用还有一定差距[10],此外,该方法中的刀柄、刀具以及主轴端的频响多依赖有限元仿真与实验模态分析,预测模型建立的工作量较大。2013 年,加拿大的LAW等[11]利用有限元方法,提出了降阶模型机床位置依赖的多体动力学建模方法,提高了机床刀尖频响预测效率。MOUSAVI等[12-13]基于矩阵结构分析(matrix structural analysis,MSA)方法的思想,利用ANSYS有限元模态仿真分析对MATLAB数值模型进行参数初步标定,再通过模态实验对未知参数进行最后标定。有限元法虽适用于对不同结构进行模态分析,但对于大型加工系统而言,随着网格数增加,计算效率显著降低,因此预测精确性与计算效率不可兼具。此外,国内外学者也提出了其他方法用于机器人铣削系统动力学分析。CHEN等[4]利用已知一定空间范围内机器人铣削位姿的实验模态参数,提出逆距离加权法,计算出任意位姿的频响函数,并验证了该方法在一定加工范围内的准确性。MOHAMMADI等[14]与PAN等[15]在研究机器人铣削中轴向振动对加工稳定性的影响,以及机器人铣削中的模态耦合颤振产生机理与抑制方法时,将机器人本体简化为质量-弹簧-阻尼模型,分别计算模型中的质量、刚度与阻尼矩阵。总体而言,对加工系统频响预测方法的研究普遍存在效率与准确性无法兼具的问题。
对于机器人铣削系统的频响预测,大都将末端主轴系统结合面考虑为刚性连接[3-5,12-15],ALTINTAS等[16]指出,将主轴-刀柄结合面看作柔性,系统的频响函数会受到影响,因此,在建模过程中不应简单地将主轴系统整体简化为刚性连接。赵万华等[17]提出一种可以考虑刀具-夹套、夹套-刀柄以及刀柄-主轴结合面接触特性的主轴转子系统动力学解析建模方法,解决了传统主轴转子系统动力学模型中的结合面接触刚度通过实验识别的方法获取时通用性差的问题。但目前在机器人铣削系统的频响预测研究中,很少对结合面接触刚度的因素进行考虑。
综上,本文提出了一种考虑主轴-刀柄结合面接触刚度的机器人铣削系统刀尖频响预测方法。将机器人本体动力学模型简化为质量-弹簧-阻尼模型,并结合欧拉-拉格朗日法、关节刚度辨识与比例阻尼模型依次确定了机器人的质量、刚度和阻尼矩阵。在此基础上,将末端执行器的质量与几何参数补偿到本体动力学模型中,并建立了主轴-刀柄结合面接触刚度解析模型,基于有限元主副自由度理论对本体模型进行二次补偿,从而构建了机器人铣削系统刀尖频响预测模型。
1 机器人铣削系统频响预测模型建立
1.1 机器人本体动力学建模
建立机器人铣削系统刀尖频响预测模型首先需要对机器人本体动力学进行建模。机器人铣削加工中进给速度远低于切削速度,因此本体动力学方程中的惯性力(即科里奥利力和离心力)影响可以忽略;同时忽略非线性惯性力的影响,考虑机器人关节柔性,将本体动力学模型简化为图1所示的质量-弹簧-阻尼线性系统[14]。同时假设工件相对于机器人系统为刚性,因此可忽略加工中的工件变形。在以上简化的基础上,机器人铣削加工系统的动力学模型可由微分方程表示:
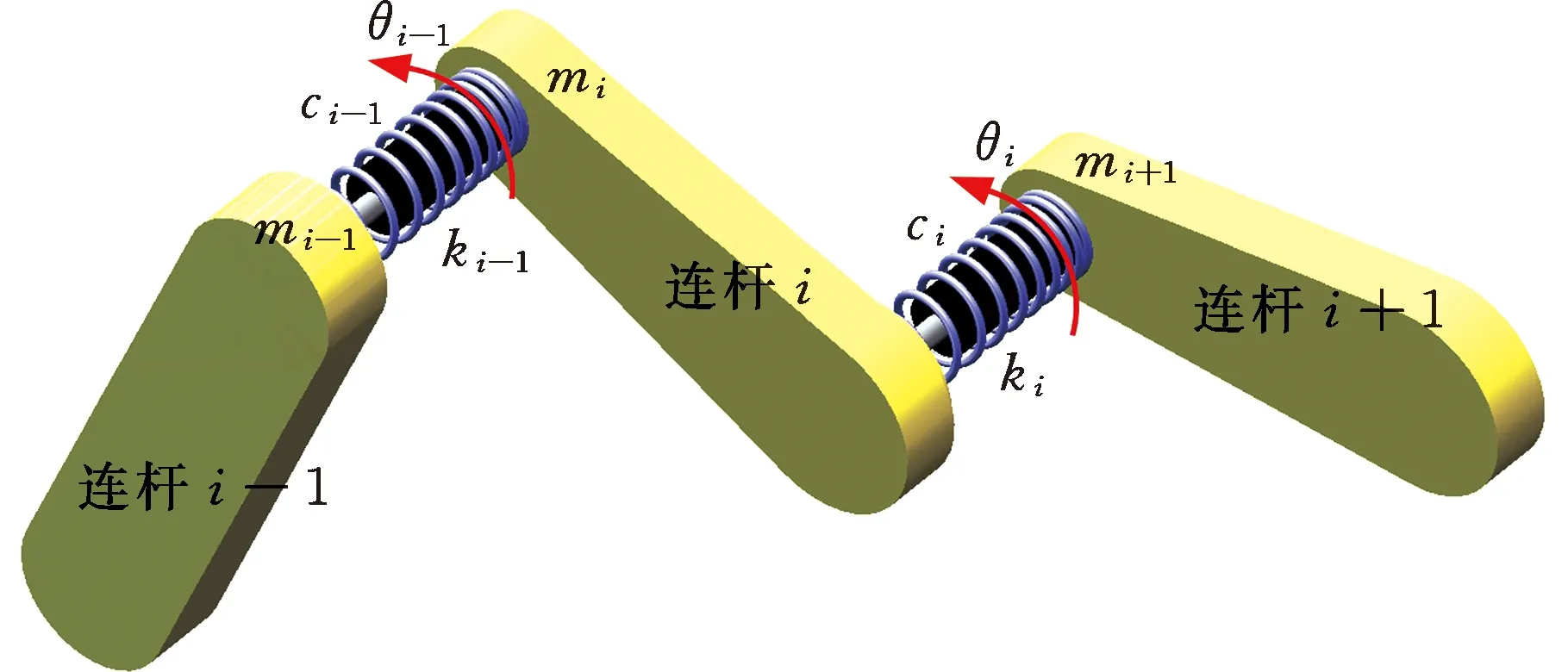
图1 机器人动力学模型简化示意图Fig.1 Simplified diagram of robot dynamics model
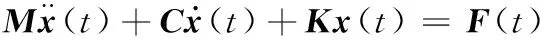
(1)
式中,M、C、K分别为机器人基坐标系中的质量、阻尼和刚度矩阵;x(t)为位移矢量;F(t)为切削力矢量。
1.1.1机器人质量矩阵计算
机器人本体动力学模型中的质量矩阵M通过将关节坐标系下的质量矩阵利用雅可比矩阵变换到基坐标系下得到:
M=J-TMqJ-1
(2)
(3)
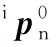
关节坐标系下的质量矩阵Mq通过KUKA KR210工业机器人惯性参数结合机器人改进D-H模型参数,利用欧拉-拉格朗日法推导得出。图2所示为实验用机器人的CAD模型,示出了该机器人通过模型导出的连杆2的质量、初始位姿下的惯性张量和基坐标系中的质心坐标。通过机器人的工作空间图提取杆长数据,建立了机器人的改进D-H模型,其D-H参数如表1所示。各个连杆的惯性参数与D-H参数作为数值模型的初始输入参数。
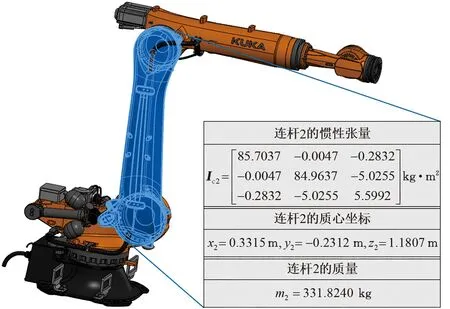
图2 KUKA KR210工业机器人CAD模型与连杆惯性参数提取Fig.2 CAD model of KUKA KR210 industrial robot and inertia parameter extraction of links
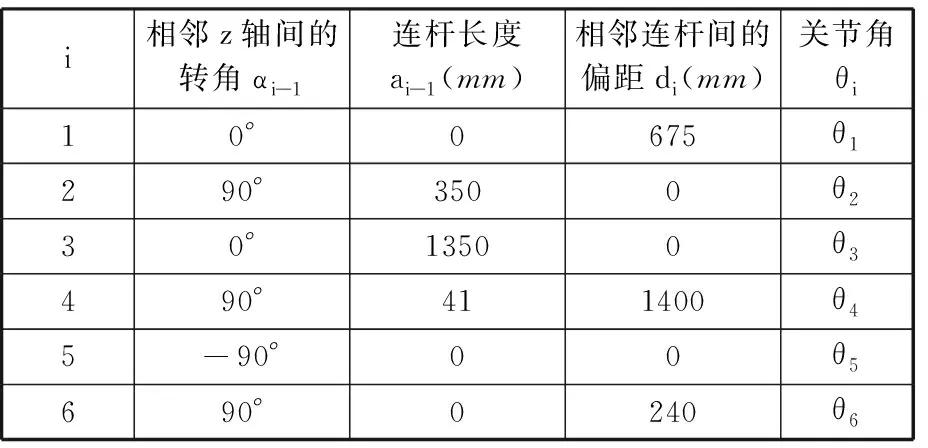
表1 KUKA KR210 型机器人的改进D-H参数表Tab.1 Modified D-H parameter table of KUKA KR210 robot
根据欧拉-拉格朗日方程[18],关节空间中的质量矩阵如下所示:
(4)
式中,mi为连杆i的质量;Jvi(q)和Jωi(q)分别为连杆i雅可比矩阵的上半部和下半部;Ri(q)为连杆i的定向变换矩阵;Ici为连杆i质心的惯性张量矩阵。
1.1.2机器人刚度矩阵计算
机器人刚度矩阵通过将关节刚度矩阵利用雅可比矩阵变换到机器人基坐标系下得到:
K=J-TKqJ-1
(5)
式中,Kq为关节坐标系下的对角刚度矩阵。
机器人各关节刚度值通过载荷实验辨识获得。在机器人法兰边缘一点施加载荷,对比加载与空载状态下的位移偏差,改变载荷质量与施力方向重复多次,根据下式:
Fo=J-TKqJ-1D
(6)
式中,Fo为外力;D为由于外力产生的位移变量。
利用最小二乘法拟合出机器人各关节刚度值。由于力矩值较小,此处只考虑测量点的位移变量。
测量对象为KUKA KR210工业机器人,采用Leica AT960/930型号的激光跟踪仪进行位移测量,实验原理和实验现场如图3所示。
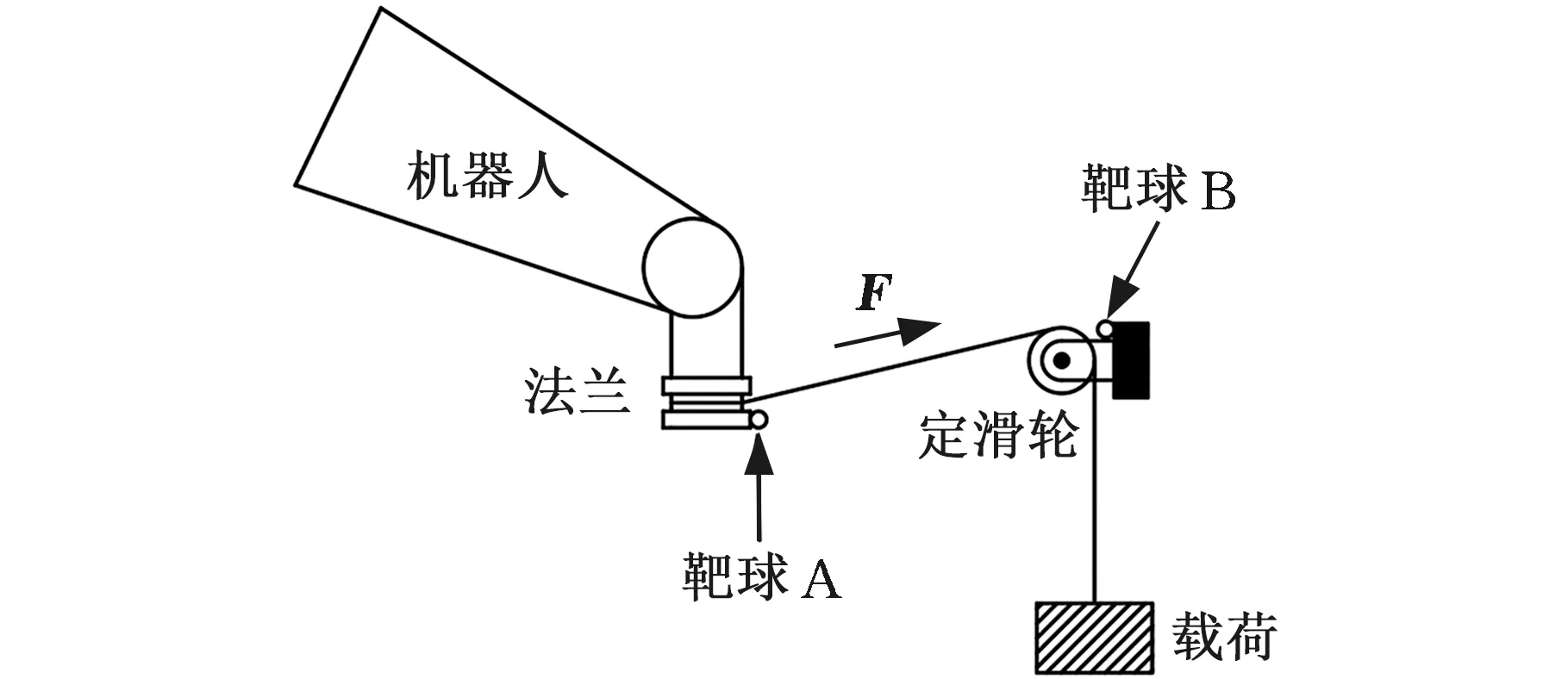
(a)实验原理

(b)实验现场图3 机器人关节刚度测试实验Fig.3 Robot joint stiffness test experiment
首先将激光跟踪仪的坐标系与机器人基坐标系重合,这样激光跟踪仪即可测量机器人基坐标系中某点坐标值。随后用绳子和滑轮装置在机器人末端分别悬挂10 kg、20 kg、30 kg的砝码;分别将靶球安装在图3b中A、B位置,利用激光跟踪仪测量向量AB的值作为力矢量F的方向(绳子方向),将砝码所施加力按照向量AB的方向余弦进行分解,即可得到基坐标系下x、y、z方向的分力。再用激光跟踪仪测得机器人末端位置空载与加载的位移变量,即可拟合关节刚度值[19]。更换滑轮C1到C2改变载荷方向重复实验。
拟合结果如下:
Kq=diag(3.3479×106,3.1318×106,4.2895×106,
2.4787×105,6.4292×105,1.8847×105) N·m/rad
(7)
1.1.3机器人阻尼矩阵计算
阻尼矩阵采用比例阻尼模型计算[20],可将其简化为已获得的质量矩阵和刚度矩阵的线性组合:
C=αK+βM
(8)
其中,α、β由刀尖频响实验标定得到。
1.2 主轴-刀柄结合面接触刚度建模
1.2.1模型建立
由于主轴系统靠近刀尖,对刀尖动力学影响较大,将主轴-刀柄结合面刚性处理会对频响函数预测精度造成误差,因此建立主轴-刀柄结合面刚度模型。
在主轴-刀柄结合面刚度建模中,同时考虑法向、切向与扭转接触刚度,采用均布的弹簧单元模拟主轴-刀柄结合面刚度特性[17],如图4a所示。将主轴与刀柄的接触区域沿轴向划分为N个单元,每个单元简化为以中径为直径的梁,每个单元的主轴面与刀柄面通过相对应节点处产生的耦合力与力矩相互作用[21],如图4b所示。
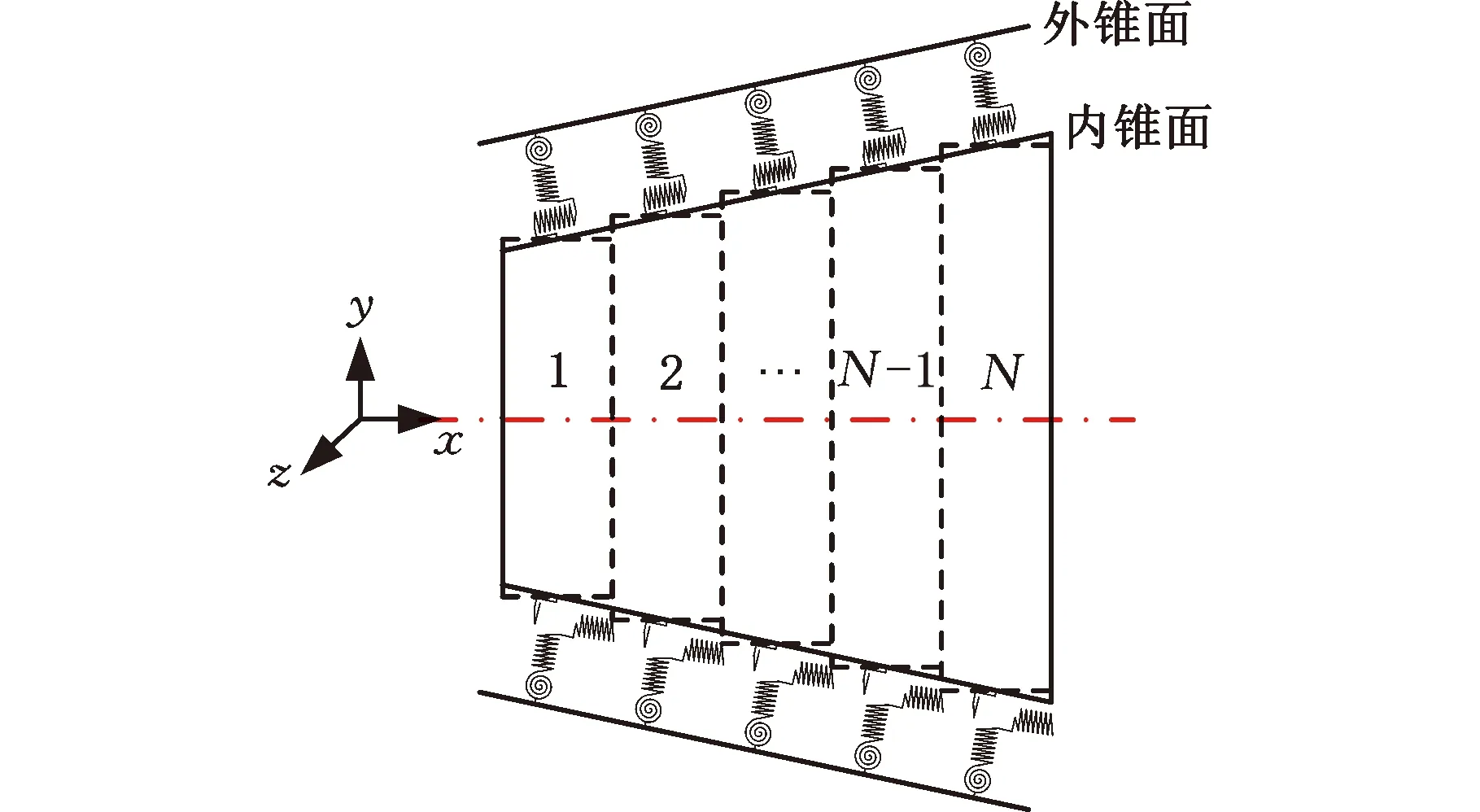
(a)结合面整体弹簧单元分布
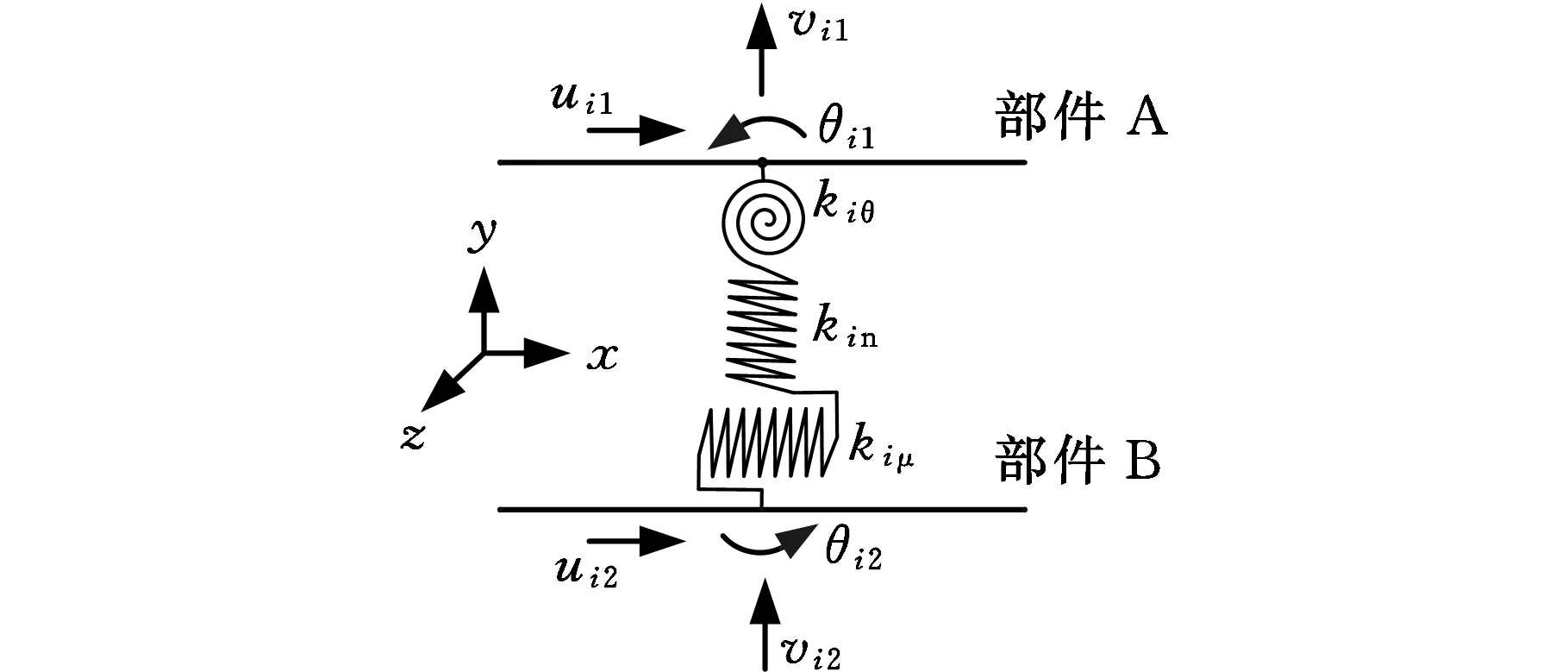
(b)结合面单元弹簧分布图4 主轴-刀柄结合面接触刚度模型Fig.4 Contact stiffness model of spindle-toolholder interface
当两个对应节点产生相对运动时,其耦合力与力矩可由下式表示:
(9)
式中,ui1、vi1、θi1分别为部件A第i个单元沿x、y和绕z方向的位移量;ui2、vi2、θi2分别为部件B第i个单元沿x、y和绕z方向的位移量;kix、kiy、kiθ分别为结合面第i个单元沿x、y和绕z方向的接触刚度;cix、ciy、ciθ分别为结合面第i个单元沿x、y和绕z方向的阻尼;Fx、Fy、Mz分别为结合面第i个单元沿x、y和绕z方向产生的耦合力与力矩。
相应的每对节点的接触刚度矩阵表示如下:
(10)
将每对节点的接触刚度矩阵kij按照有限元法组装即可得到整个结合面的总刚度矩阵KJ。
式(10)矩阵中接触刚度kix、kiy和kiθ需要通过对主轴-刀柄结合锥面的法向、切向与角接触刚度进行计算进而变换到机器人的基坐标系下获得。
图5为刀柄的受力示意图,静态下,主轴拉刀力使结合面产生接触刚度。
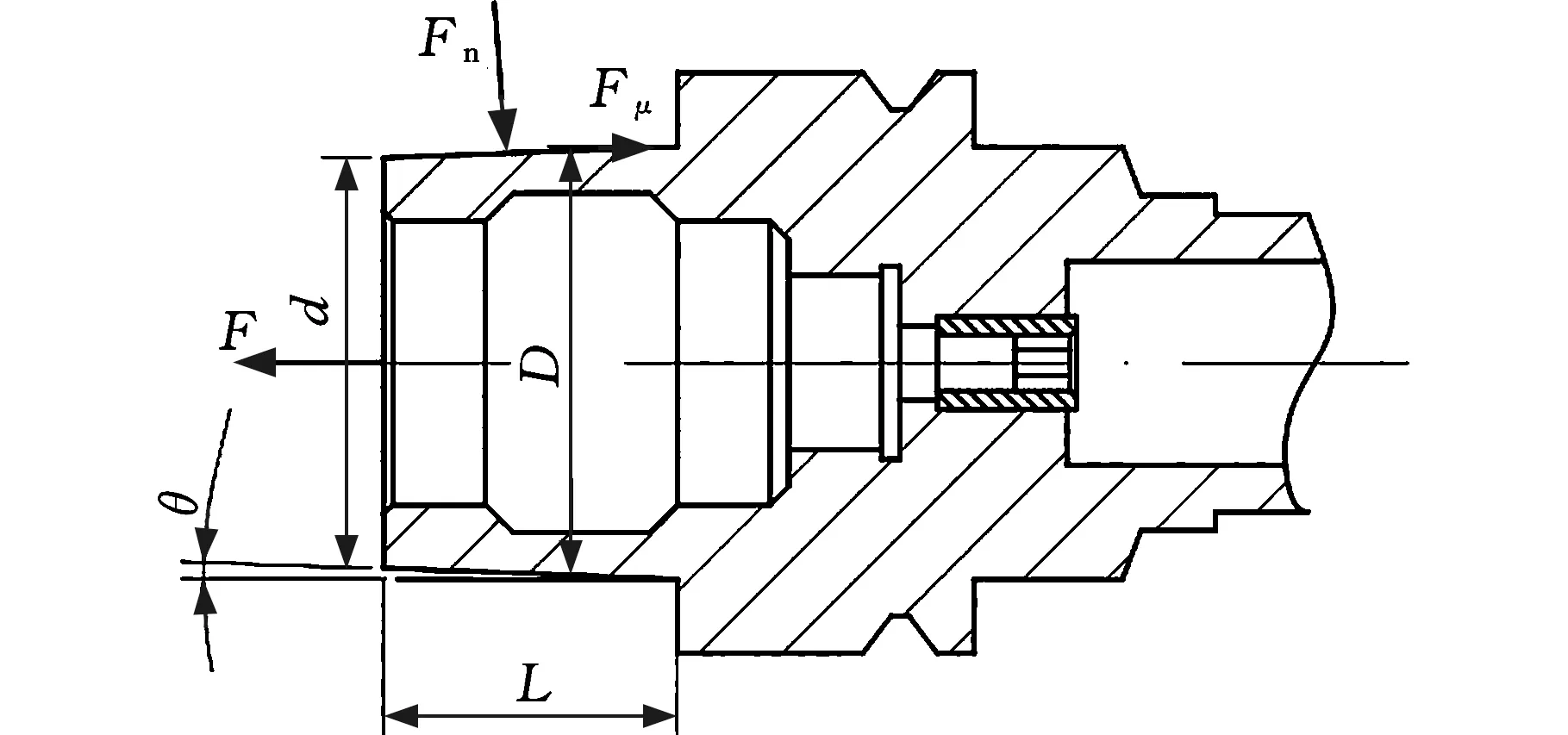
图5 刀柄结合锥面受力示意图Fig.5 Force diagram of toolholder joint
平衡方程为
(11)
式中,F为主轴拉刀力;Fn为结合锥面所受法向正压力;Fμ为结合锥面所受切向摩擦力;θ为锥角;μ为锥面摩擦因数。
刀柄接触面的法向正压力为
(12)
主轴-刀柄结合面接触面积为
(13)
式中,Di为刀柄结合锥面第i个单元的大径尺寸;di为刀柄结合锥面第i个单元的小径尺寸;Li为刀柄结合锥面第i个单元的轴向长度。
主轴-刀柄结合面第i个单元所受压力为
(14)
根据吉村允孝的单位面积法[22],第i个单元的法向接触刚度为
(15)
式中,α′、β′为结合面基础特性参数,由实验拟合得到。
结合面的切向刚度系数一般为法向刚度系数的1/3~2/3[22],本文取每个单元的切向接触刚度为其法向接触刚度的1/2。
主轴-刀柄结合锥面第i个单元的角接触刚度为
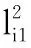
(16)
(17)
(18)
式中,kit为主轴-刀柄结合锥面的切向接触刚度;li1与li2为几何相关系数;Dim为主轴-刀柄结合面第i个单元中径。
角接触刚度的详细计算原理见文献[17]。
1.2.2结合面刚度矩阵的降阶变换
有限元法将连续体(无限多自由度的系统)离散为有限的N阶自由度系统[23],而本模型只考虑较低阶模态,为最终简化为二自由度系统,需要将总刚度矩阵KJ的维数进一步减小。利用有限元方法中的主副自由度理论,按照加速动力缩聚法,将矩阵左上角一定维数的元素定为主自由度,其他部分作为副自由度[24],进行矩阵变换。
将主自由度记为δa,副自由度记为δb,总刚度矩阵按照所选取的主副自由度个数分块表示:
(19)
只考虑主副自由度间的弹性联系,则主副自由度间满足以下约束方程:
Kbaδa+Kbbδb=0
(20)
由此可得
(21)
(22)
(23)
式中,T为变换方程,是一个长方形矩阵。
将总刚度矩阵KJ变换为所需的低阶刚度矩阵:
(24)
最后,综合考虑机器人本体与末端执行机构的动力学以及主轴-刀柄结合面接触刚度,将式(24)代入式(1)中,加工系统的整体动力学方程如下:
(25)
2 模型标定与实验验证
2.1 模型标定
由于机器人执行末端结构较复杂,几何、材料等相关数据无法准确获取,另外阻尼系数未知,因此需要对这些参数进行标定。在将末端执行器与机器人第六轴看作刚性连接的情况下,选择预测模型中第六轴的质量m6与杆长d6作为调整参数来标定仿真频响函数的固有频率,选择阻尼系数α、β作为调整参数来标定仿真频响函数的幅值。本文利用模态实验获得不同位姿下的多组系统刀尖频响函数,基于建立的考虑主轴-刀柄结合面接触刚度的机器人铣削系统动力学模型,通过使实验与数值仿真得到的频响函数的固有频率及其峰值差值最小化,来识别数值模型中以上的未知参数[13]。根据下面的公式通过数值模型计算得到频响函数:
(26)
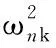
式中,ωnk、ηk分别为数值模型的第k阶模态的固有频率和阻尼比;pik、pjk为数值模型的第k阶模态的振型矢量;Fj(ω)和Xi(ω)分别为在数值模型自由度j上的激励力和自由度i上的位移量。
将1.1.1节与1.1.3节得到的质量矩阵与阻尼矩阵转化到模态空间后,可得到第k阶模态质量mk和模态阻尼ck。
加工系统安装的是FIACHER SD5084型号的主轴和TRIBOS-S HSK-E32型号的刀柄。实验设备使用安装有YD-5T型石英传感器的力锤敲击刀尖产生激励信号,使用INV9822型加速度传感器采集刀尖处的响应信号,加速度传感器灵敏度为10.355 mV/(m·s-2),采用INV3062T型4通道数据采集卡,采样频率设置为5120Hz。最后利用此套设备配备的模态分析模块计算得到实验频响函数。机器人铣削系统与信号采集设备和实验示意图见图6。

(a)系统与采集设备

(b)实验示意图图6 实验设备与测试示意图Fig.6 Experimental equipment and test diagram
标定过程如图7所示。首先进行频率标定,调整m6、d6两参数使仿真频响的固有频率与实验重合,如图7b所示;再进行阻尼标定,调整α、β两参数使仿真频响的峰值与实验重合,如图7c所示;此过程改变位姿重复进行多次,优化所选参数的标定值。
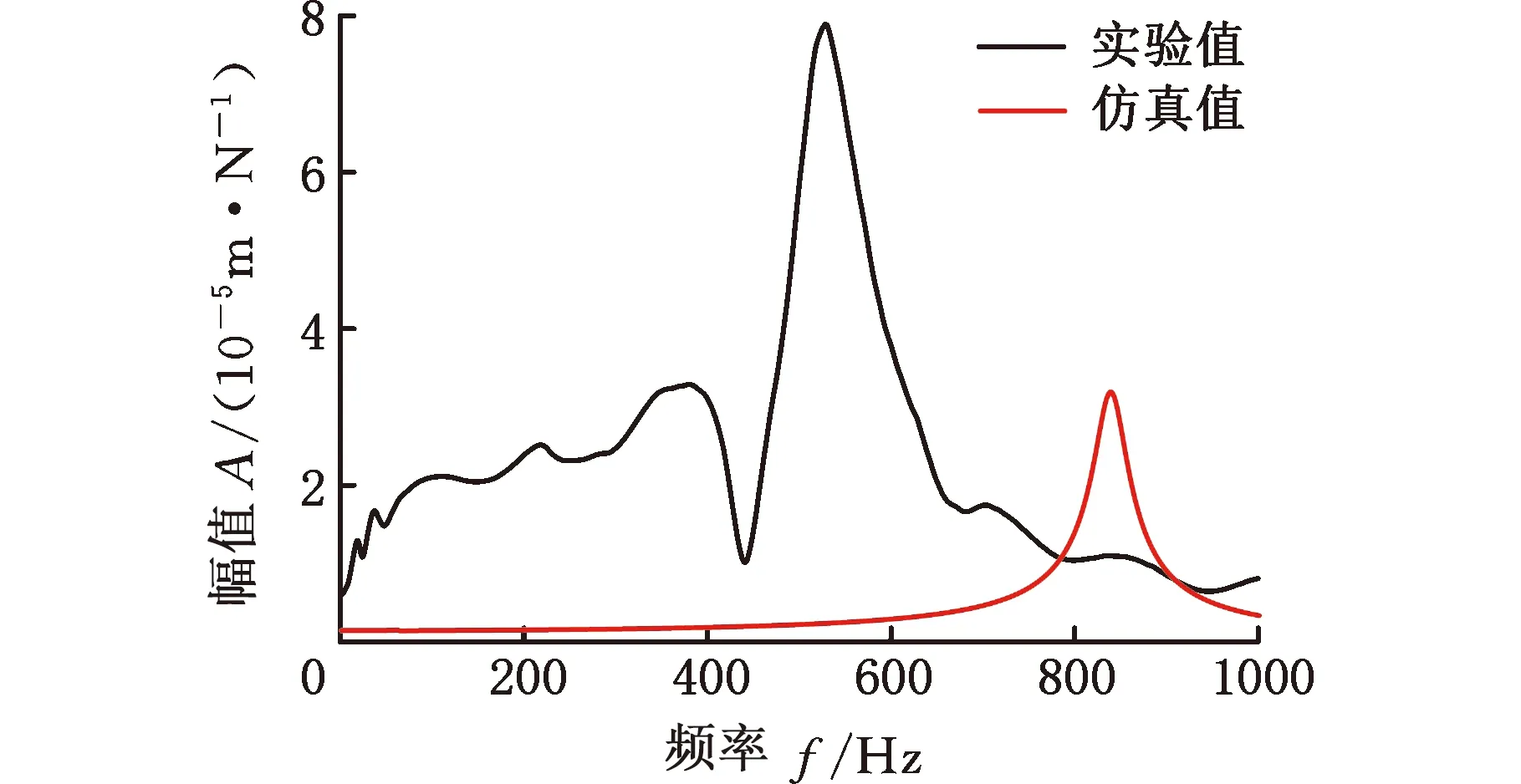
(a)未标定
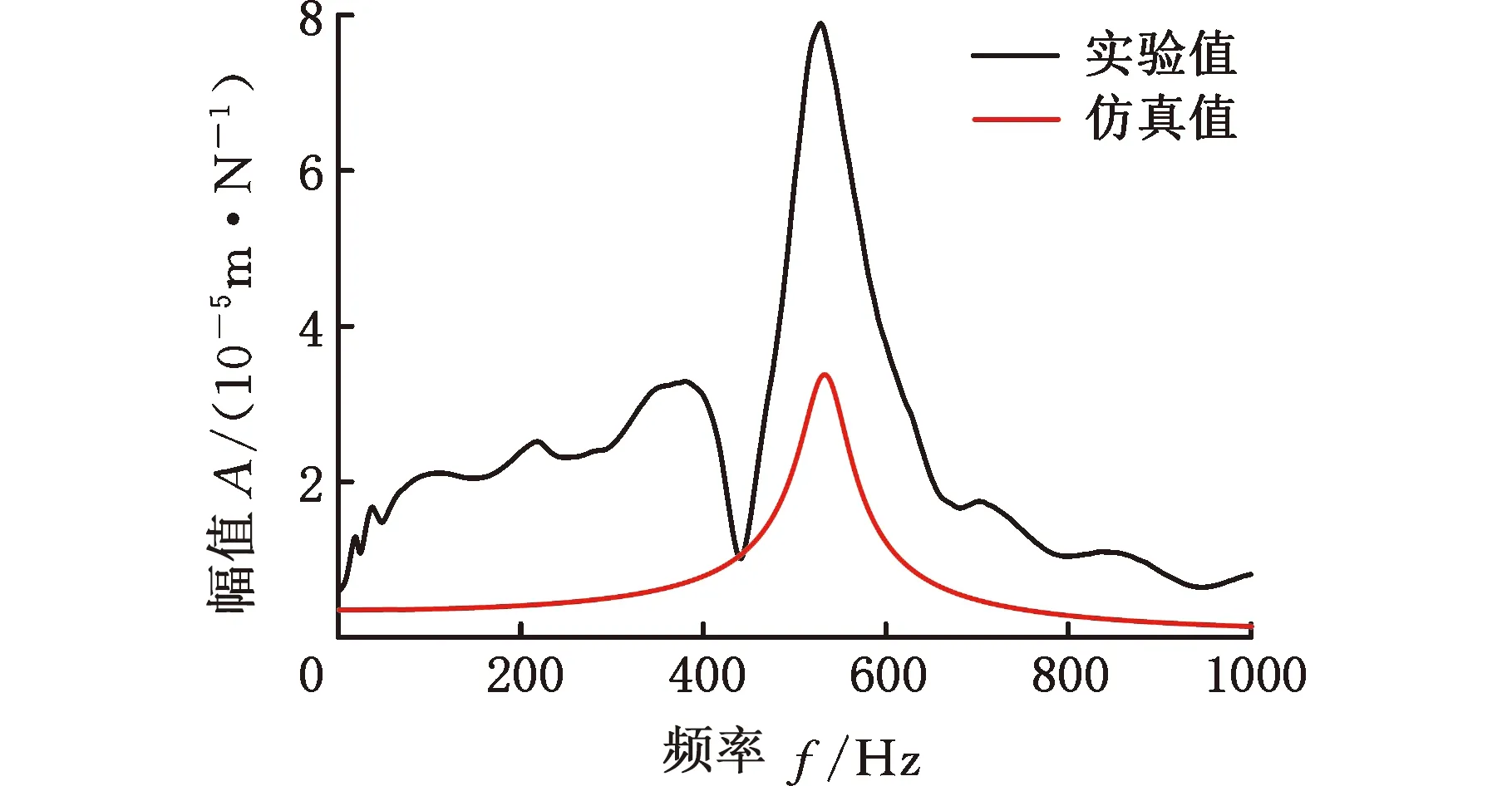
(b)频率标定
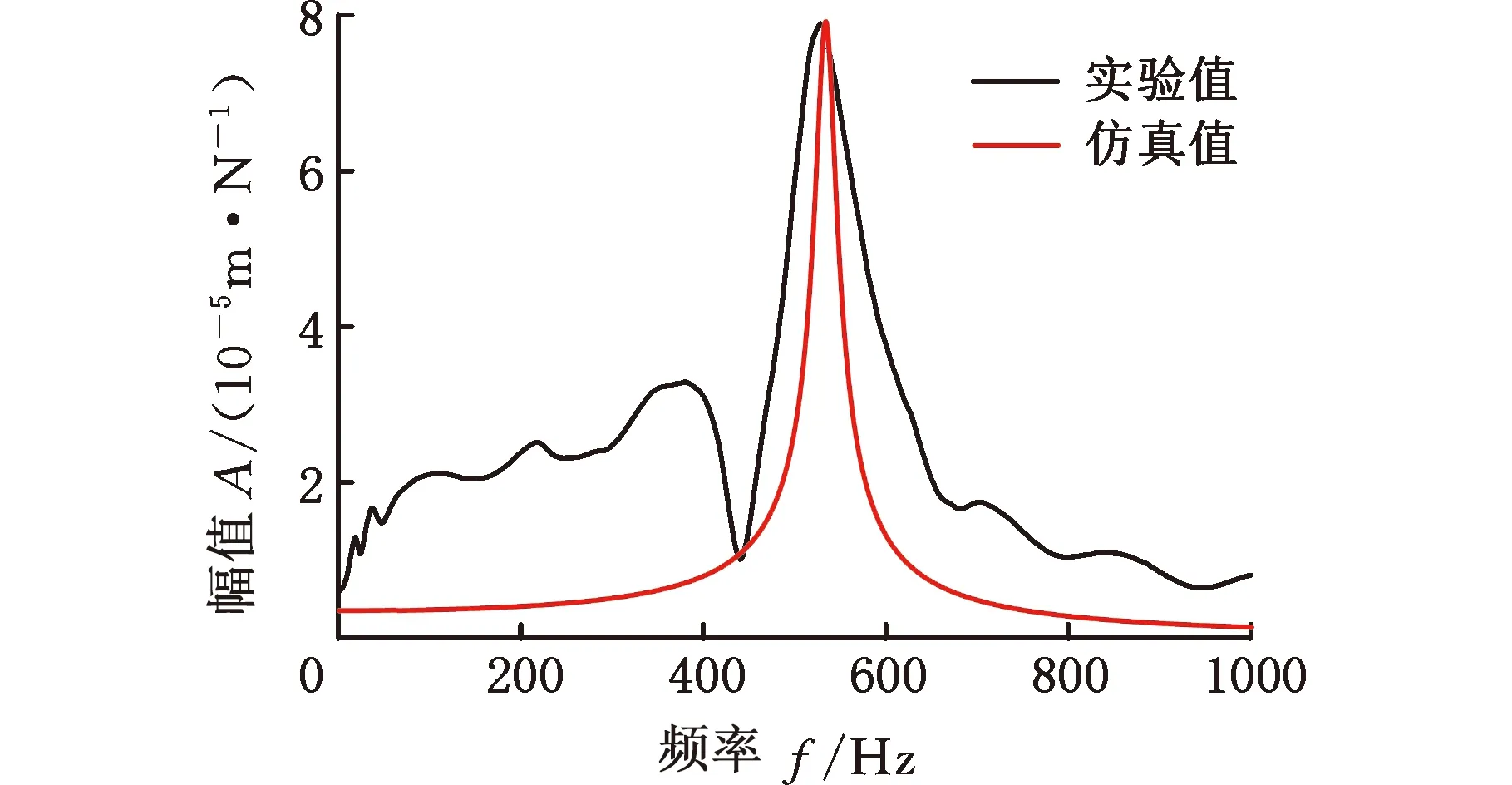
(c)阻尼标定图7 数值模型标定过程示意图Fig.7 Numerical model calibration process diagram
2.2 实验验证
为验证机器人铣削系统刀尖频响函数预测模型的准确性,开展刀尖频响函数测试实验。实验随机选取机器人的5个位姿,如表2所示,采用锤击法对刀尖频响函数进行测试,并与上述数值模型计算得到的频响结果对比,以验证本文提出的数值模型的准确性。
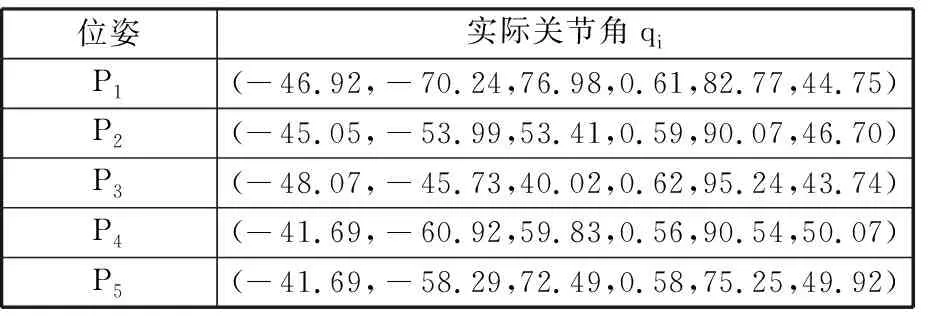
表2 所选机器人位姿的各关节角Tab.2 Joint angles of the selected robot postures
采用式(26)的频响预测数值模型对以上所选的机器人位姿进行仿真频响计算。在主轴-刀柄结合面接触刚度矩阵计算中,将刀柄与主轴的结合面沿轴向划分为6个单元,每个单元建立一组弹簧模型。本文所用主轴与刀柄接触部分材料为钢,在无润滑接触情况下,主轴与刀柄的摩擦因数μ取为0.15,结合面基础特性参数α′、β′依据文献[22]分别选取为3 262 540与0.604。
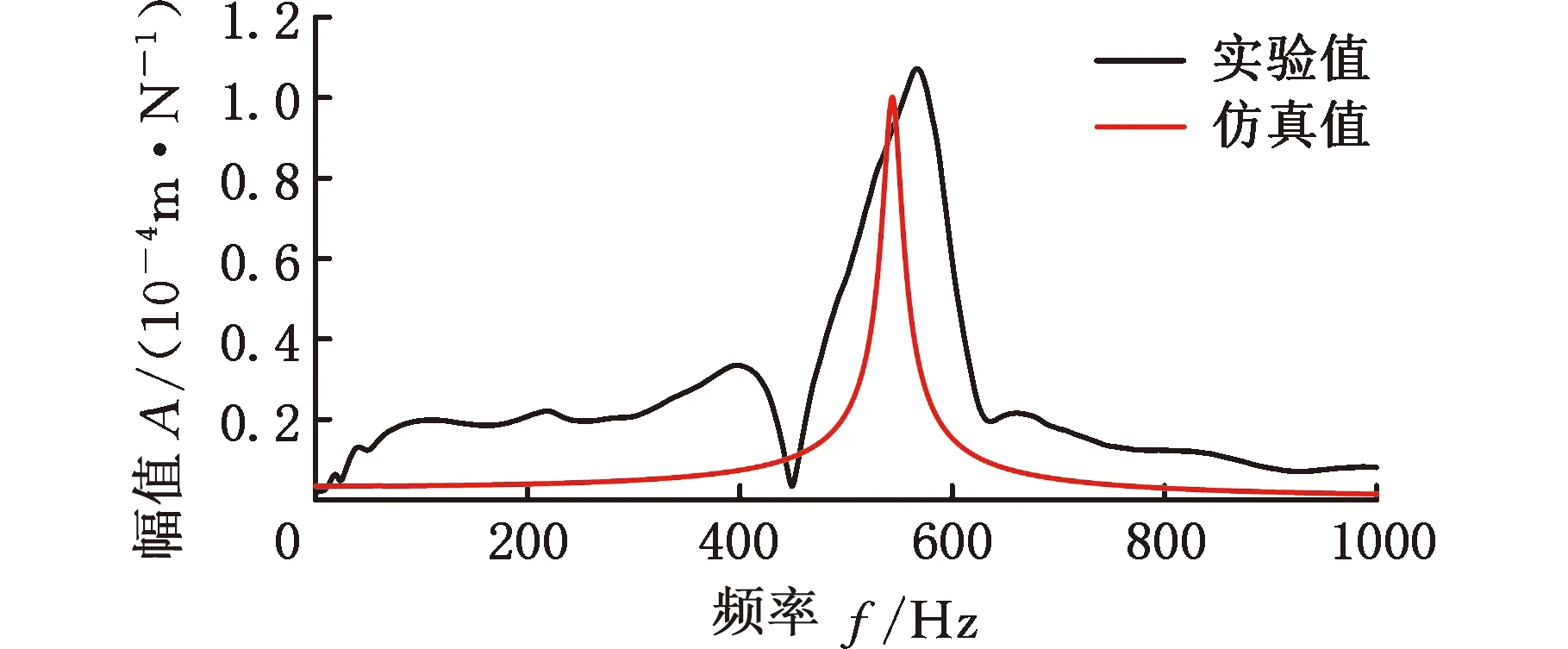
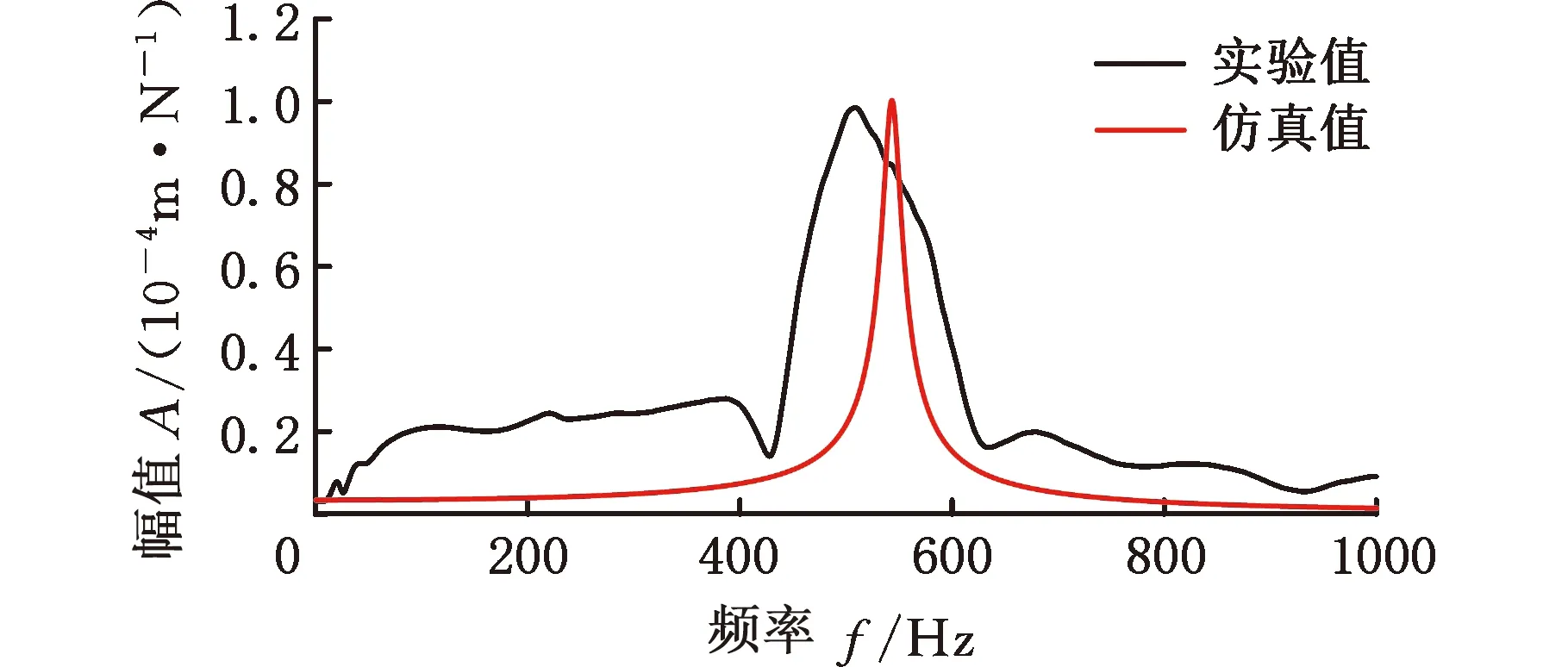
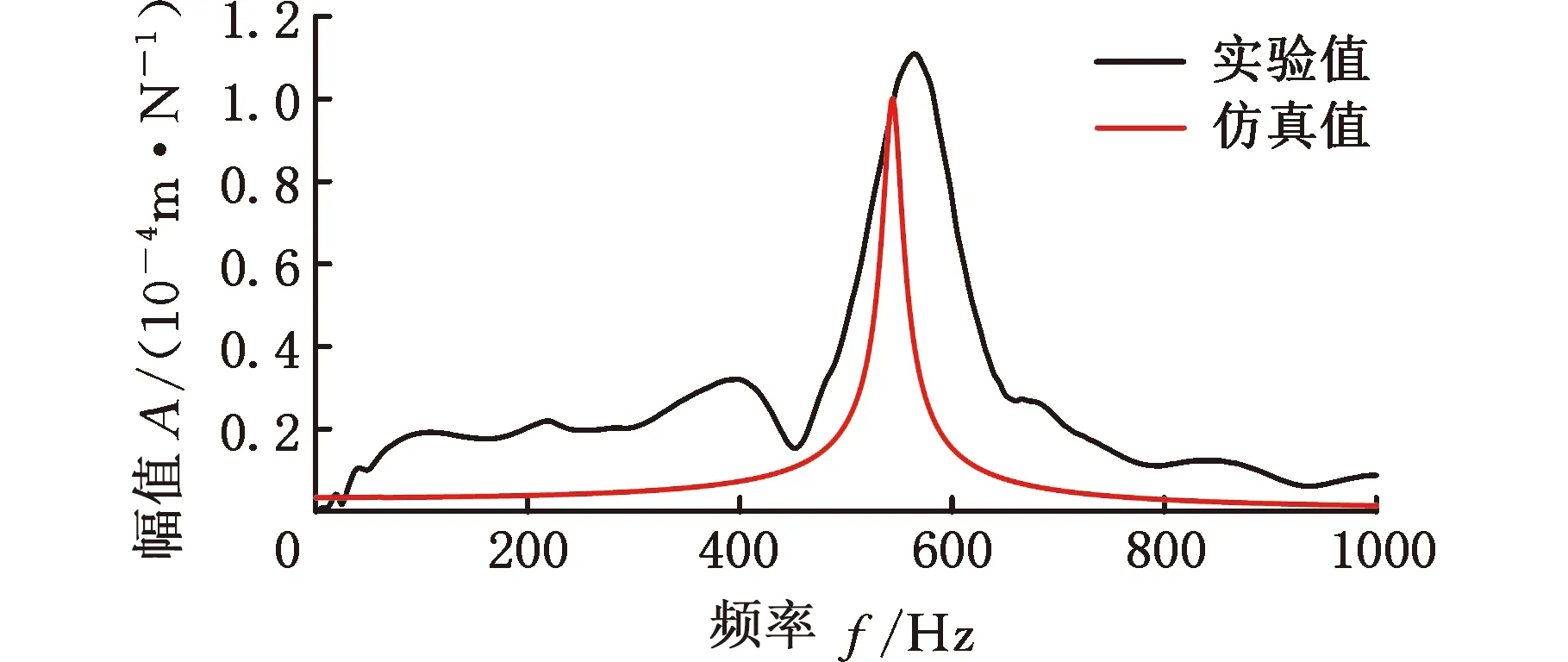
所选位姿下刀尖频响的实验与仿真对比结果如图8所示,表3给出各位姿下仿真与实验得到的幅值与固有频率以及两者的相对误差。实验所得频响函数随位姿变化,这是不同位姿下加工系统的动力学特性有所改变导致的。提出的预测模型将机器人各关节角度作为变量,考虑了位姿变化的影响,结果表明,提出的机器人铣削系统刀尖频响预测方法计算出的频响函数与实验得到的频响函数相比,固有频率误差最大不超过6.63%,幅值误差最大不超过9.80%,验证了考虑主轴-刀柄结合面接触刚度的机器人铣削系统刀尖频响预测方法的有效性。造成仿真结果与实验结果之间误差的原因如下:①所用加速度传感器的自身质量在测量时会对刀尖动力学造成一定影响;②实验所用模态分析软件在将加速度信号进行两次积分算得位移信号时不可避免地产生计算误差;③对模型的简化造成一定误差,如将末端执行器与机器人法兰看作完全刚性连接等。
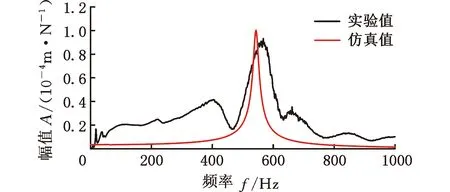
(a)P1
(b)P2
(c)P3
(d)P4
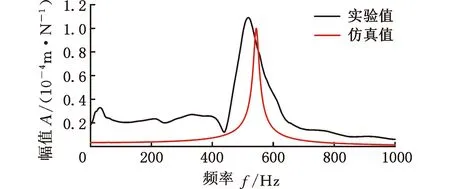
(e)P5图8 所选位姿下刀尖频响实验与仿真对比结果Fig.8 Comparison of experimental and simulation results of tool tip frequency response under selected postures
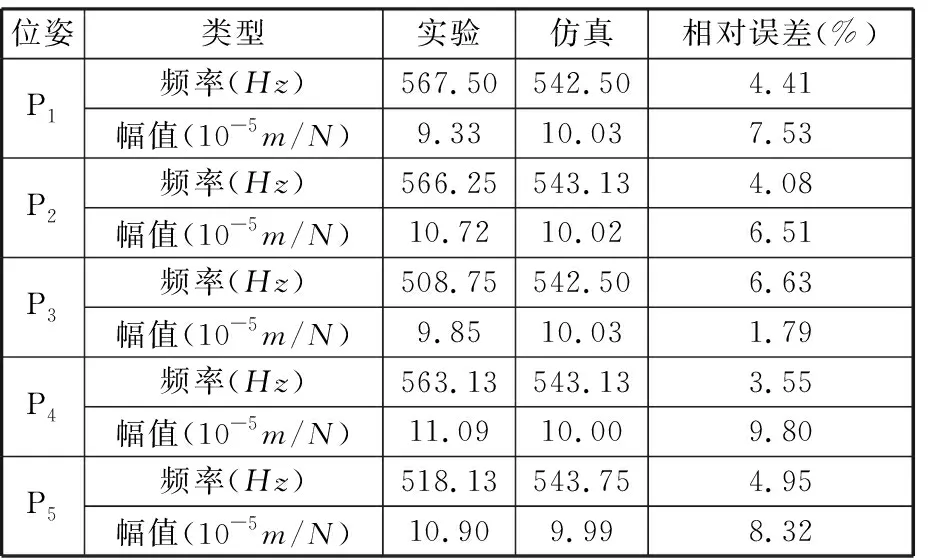
表3 由模态实验与数值模型得到的刀尖频响结果对比Tab.3 The comparison of tool-tip frequency responses obtained by modal experiment and numerical model
3 结论
通过机器人本体动力学模型与末端结合面动力学模型叠加,提出一种考虑主轴-刀柄结合面接触刚度的机器人铣削系统刀尖频响预测方法,并通过加工系统的刀尖模态实验进行验证,结果表明,随机位姿下实验与模型仿真的误差都能控制在10%以内,说明所述方法可准确预测机器人铣削系统的刀尖频响函数,减小了对大量实验结果的依赖,并在保证足够预测精度的基础上简化了模型建立过程,提高了计算效率。
